Что такое монада в программировании
Монады с точки зрения теории категорий
Мы начнём с простого введения в категории и функторы, затем дадим определение монады, приведём простые примеры монад в категориях и в конце приведём монадическую терминологию используемую в языках программирования.
Я уверен, что монады с точки зрения категорий почти элементарны.
Содержание
Категория
Категория состоит из объектов и морфизмов между ними. Термин «морфизм» не совсем корректен (он не обязан превращать что-то), по этому, часто, морфизм называют «стрелкой» для того, чтобы показать его абстрактную сущность.
Мы будем использовать термин «стрелка» во всех случаях, кроме того, когда стрелка обозначает некоторую функцию, тогда мы будем называть её «морфизм», но для меня он всё равно останется стрелкой.
Неважно, чем является объект или стрелка, важно только выполнение следующих свойств:
Замечание. В виду чрезвычайно абстрактной природы этой записи, мы не можем ожидать, что «все объекты» или «все стрелки из a к b» образуют множество. Категории, где они являются множествами называются «малые» или «локально малые».
Примеры категорий
Дополнительный материал
Образуют ли сами категории категорию? Да, но тогда нам следует дать определение стрелок между ними. Они являются стрелками второго порядка и называются функторами.
Функтор
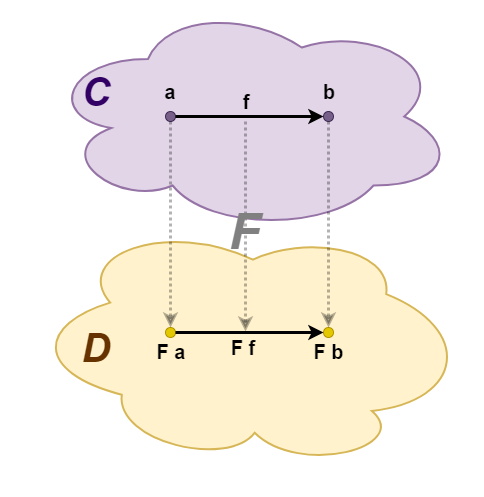
Функтор отображает одну категорию в другую. Для того, чтобы сделать это, нам нужно отобразить объекты из первой категории во вторую и стрелки (морфизмы) из первой категории в стрелки второй категории непротиворечивым образом.
Примеры функторов
Упражнение. Определите такое же расширение для частичных функций.
Естественное преобразование
По этому оно называется «естественным» — оно действует непротиворечиво с действиями функторов на стрелки.
Примеры естественных преобразований
Опять же, это определение можно записать следующим образом:
Монада
Примеры монад
Помните, что мы можем считать частично-упорядоченные множества и их функции, сохраняющие порядок, как категории и функторы?
Эти два условия являются ни чем иным, как аксиомами монад, применёнными к частично-упорядоченным множествам, считая, что монады в частично-упорядоченных множествах и есть замыкания. Также можно попытаться применить это к частично-упорядоченным множествам путей графа.
Монады исключения и состояния
Монада исключения
Монада состояния
Скучное упражнение. Докажите, что это действительно монада.
Монады в программировании
Преимущество такой модели состоит в том, что мы можем погрузить все наши высказывания относительно программ в очень стабильную теорию категорий; возможно менять сущность объектов и категорий, изменять логику лежащего в основе топоса и быть на 100% уверенными в том, о чем мы говорим. Например, вместо «нечёткой логики» можно использовать интуиционистскую логику или семнтику Крипке.
Кажется, что некоторые техники программирования не подходят для такой модели, например исключения или побочные эффекты.
А для функций имеющих состояние подойдёт, соответственно, монада состояния.
Монада IO в Haskell
В Haskell ввели монаду IO, чтобы избежать сложности с описанием того, каким образом функции могут иметь побочные эффекты.
Они использовали следующий трюк. Возьмите монаду состояния, как мы делали до этого. Вообразите, что A это множество состояний, представляющее внешний мир, а X это множество результатов функции.
Интересно, чего же конкретно они пытались этим добиться.
Монады с точки зрения программистов (и немного теории категорий)
Введение
Как узнать, что человек понял, что такое монады? Он сам вам об этом расскажет в первые 5 минут общения и обязательно попробует объяснить. А ещё напишет об этом текст и по возможности где-нибудь его опубликует, чтобы все остальные тоже поняли, что такое монады.
Среди функциональных программистов, особенно на Haskell, монады стали чем-то вроде локального мема. Их часто пытаются объяснить, отталкиваясь от частных случаев и сразу приводя примеры использования. Из-за этого слушатель может не уловить основную суть понятия, а монады так и останутся чёрной магией, ну или просто средством костылизации побочных эффектов в чисто функциональных языках.
Я сначала расскажу про базовые понятия теории категорий, а затем мы с практической точки зрения подойдём к определению монады и увидим, что на самом деле очень многие программисты пользуются этой мощной абстракцией в одном из её проявлений.
Моё изложение во многом основывается на книге Бартоша Милевски «Теория категорий для программистов», которая создавалась как серия блогпостов, доступна в PDF, а недавно вышла в бумаге.
Примеры приводятся на Haskell, предполагается, что читатель знаком с синтаксисом и основными понятиями языка. В упомянутой книге есть примеры и на С++, можете сравнить чистоту и понятность кода.
Категории
Определение
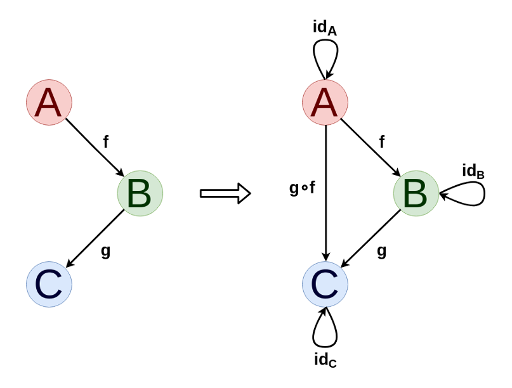
Категории сами по себе — очень простые конструкции. Категория — это набор объектов и морфизмов между ними. Морфизмы можно рассматривать как однонаправленные стрелки, соединяющие объекты. В общем случае про сущность самих объектов ничего не известно. Теория категорий работает не с объектами, а с морфизмами, точнее — с их композицией.
Используется следующая нотация:
В определении категории на морфизмы накладываются дополнительные ограничения:
Существуют два важных свойства, которым должна удовлетворять любая категория (аксиомы теории категорий):
Категории очень легко и естественно визуализируются как ориентированные графы. В принципе, любой ориентированный граф можно достроить до категории, добавив композиции морфизмов и тождественные морфизмы, если необходимо.
Объекты и морфизмы не обязательно образуют множества (в классическом смысле из теории множеств), поэтому в общем случае используется словосочетание «класс объектов». Категории, в которых классы объектов и морфизмов всё-таки являются множествами, называются малыми категориями. Далее мы будем работать только с ними.
Типы и функции
Композиция морфизмов — это композиция функций, причём синтаксис этой операции на Haskell почти идентичен математической нотации:
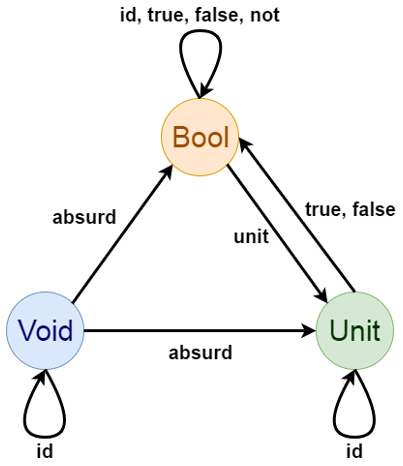
Рассмотрим несколько примеров типов с точки зрения теории категорий.
Множество из двух элементов — логический тип Bool :
Добавив тождественные морфизмы, получим следующую категорию:
В дальнейшем изложении будем использовать Haskell-подобную нотацию сигнатуры типов для обозначения морфизмов.
Функторы
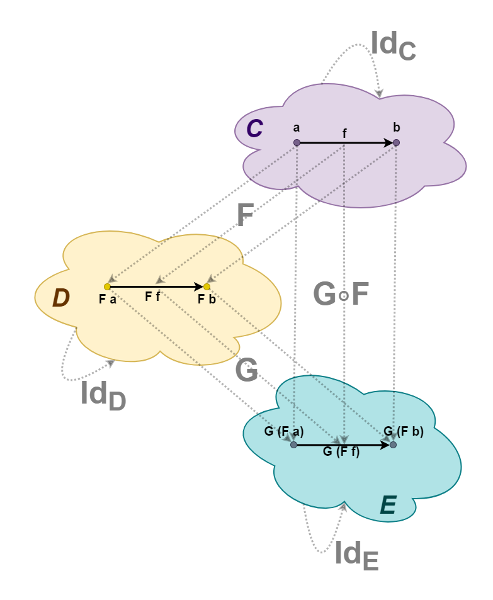
Кроме того, должны выполняться «законы сохранения» композиции и тождественного морфизма:
Таким образом, функтор не «ломает» структуру категории: то, что было связано морфизмом в исходной категории, будет связано и в результирующей. Это верно и для крайних случаев, например, когда результирующая категория состоит из одного объекта. Тогда все морфизмы исходной категории отобразятся в тождественный морфизм для этого объекта, но упомянутые выше законы нарушены не будут.
Посмотрим на эту картинку сильно издалека, так, чтобы сами категории превратились в точки-объекты, а функторы — в стрелки между ними (морфизмы). Получим категорию малых категорий, которая называется Cat (название периодически порождает сложные мемы с кошками).
Вернёмся к категории типов языка Haskell и будем работать с эндофункторами в этой категории. Они преобразуют типы в другие типы и, кроме того, каким-то образом преобразуют функции, работающие с этими типами.
Конструктор типа Maybe является примером такого функтора, он преобразует тип a в тип Maybe a (сам по себе Maybe не является типом!):
Монады
Все функции, которые были рассмотрены до этого, были чистыми, т.е. предполагалось, что у них нет побочных эффектов. Это функции в математическом смысле: результат чистой функции зависит только от значения её аргумента, он не меняется из-за места или времени вызова.
Поставим перед собой задачу логгировать вызовы функций. На императивном языке проще всего было бы хранить лог как глобальное состояние, которое изменяется в теле каждой функции. Программирование на функциональных языках не располагает к использованию глобального состояния, поэтому будем решать поставленную задачу, оперируя имеющимися у нас чистыми функциями — морфизмами в категории типов языка Haskell.
Типы функций позволяют составить их композицию:
Чтобы не отвлекаться на сложности реализации, в качестве представления лога возьмём просто строку. Мы хотим, чтобы после применения функции processString в логе содержалась запись «upCase toWords».
Запись в лог — побочное действие функций, мало относящееся к их основному функционалу. Хотелось бы во-первых, добавить информацию на уровне типов о том, что будет выполняться логгирование, и во-вторых, минимизировать дополнительные действия, которые придётся проделать сторонним разработчикам для работы с этими функциями.
Создадим новый тип данных, который будет помимо самих значений типа a хранить ещё и строку, в которую каждая вызванная функция будет добавлять своё имя.
Заметим, что Writer — это функтор, мы легко можем описать для него функцию fmap :
Преобразуем функции upCase и toWords и сделаем так, чтобы они возвращали значение, «завёрнутое» в тип Writer :
Теперь мы больше не можем записать композицию этих функций так же, как раньше, из-за несоответствия типов. Определим специальную функцию для композиции, которая сначала получает значение типа b и первую строку, передаёт это значение второй функции, получает значение типа c и вторую строку и в качестве финального результата возвращает значение типа c и конкатенацию строк, полученных при вычислении:
Реализация функции processString принимает вид:
Для того, чтобы получить настоящую категорию с такими морфизмами, необходимо определить ассоциативную композицию морфизмов и тождественный морфизм для каждого объекта таким образом, чтобы соблюдались аксиомы теории категорий. Тогда полученная категория называется категорией Клейсли, а функтор m — монадой. На Haskell это определение выглядит так (везде далее используются типы из категории Hask):
Например, для типа Writer реализация будет следующей:
Мы пришли к третьему определению класса Monad :
Здесь присутствует явное требование на то, чтобы m был функтором. Это ограничение не было нужно для предыдущих определений, поскольку функция fmap реализуется через >>= :
Практическое применение монад
Приведём примеры практического применения монад для решения задач, которые традиционно решаются с использованием «нечистых» функций и побочных эффектов.
Недетерминированные вычисления
Абстракция недетерминированных вычислений (т.е. таких, у которых может быть несколько возможных результатов) реализуется с помощью списков.
Тогда оператор >>= можно записать так:
Резюмируем эти реализации в классическом определении класса Monad :
Конечно, список как результат функции не обязательно обозначает недетерминированность вычислений. Хорошим примером, когда это действительно так, является реализация искусственного интеллекта для игр. Список может представлять возможные результаты хода игрока, ответных ходов может быть тоже несколько — всё время приходится работать со списками, списками списков и т.д.
Исключения
Простейшая реализация обработки исключений в чистых функциях состоит в добавлении в тип возвращаемого значения специального варианта, обозначающего, что что-то пошло не так.
Определение методов класса Monad для Maybe :
Для классификации ошибок можно использовать перечислимый тип или любую другую структуру данных, подходящую для конкретной задачи. Мы в примерах продолжим использовать просто строку. Введём синоним типа для работы с исключениями:
Композиция функций описывается аналогично случаю с использованием Maybe :
Определение экземпляра класса Monad уже не должно вызывать трудностей:
Состояния
Объявим синоним типа для работы с состоянием:
Фиксируем тип состояния s и покажем, что State s является функтором. Нам понадобится вспомогательная функция runState :
Реализация класса Functor :
Конечно, в реализации Unit можно опустить. Здесь он добавлен для того, чтобы показать эту операцию с точки зрения теории категорий.
Тип IO — один из первых, о котором узнаёт начинающий пользователь Haskell, и наверняка сразу встречает пугающее слово «монада». Такой упрощённый взгляд на этот тип как на состояние для работы с внешним миром может помочь понять, почему это так. Кончено, это описание очень поверхностно, но полноценный рассказ о том, как на самом деле реализован ввод-вывод, зависит от компилятора и выходит далеко за рамки статьи.
Монады с точки зрения программистов (и немного теории категорий)
Как узнать, что человек понял, что такое монады? Он сам вам об этом расскажет в первые 5 минут общения и обязательно попробует объяснить. А ещё напишет об этом текст и по возможности где-нибудь его опубликует, чтобы все остальные тоже поняли, что такое монады.
Среди функциональных программистов, особенно на Haskell, монады стали чем-то вроде локального мема. Их часто пытаются объяснить, отталкиваясь от частных случаев и сразу приводя примеры использования. Из-за этого слушатель может не уловить основную суть понятия, а монады так и останутся чёрной магией, ну или просто средством костылизации побочных эффектов в чисто функциональных языках.
Я сначала расскажу про базовые понятия теории категорий, а затем мы с практической точки зрения подойдём к определению монады и увидим, что на самом деле очень многие программисты пользуются этой мощной абстракцией в одном из её проявлений.
Моё изложение во многом основывается на книге Бартоша Милевски «Теория категорий для программистов», которая создавалась как серия блогпостов, доступна в PDF, а недавно вышла в бумаге.
Примеры приводятся на Haskell, предполагается, что читатель знаком с синтаксисом и основными понятиями языка. В упомянутой книге есть примеры и на С++, можете сравнить чистоту и понятность кода.
Категории
Определение
Категории сами по себе — очень простые конструкции. Категория — это набор объектов и морфизмов между ними. Морфизмы можно рассматривать как однонаправленные стрелки, соединяющие объекты. В общем случае про сущность самих объектов ничего не известно. Теория категорий работает не с объектами, а с морфизмами, точнее — с их композицией.
Используется следующая нотация:
В определении категории на морфизмы накладываются дополнительные ограничения:
Существуют два важных свойства, которым должна удовлетворять любая категория (аксиомы теории категорий):
Категории очень легко и естественно визуализируются как ориентированные графы. В принципе, любой ориентированный граф можно достроить до категории, добавив композиции морфизмов и тождественные морфизмы, если необходимо.
Объекты и морфизмы не обязательно образуют множества (в классическом смысле из теории множеств), поэтому в общем случае используется словосочетание «класс объектов». Категории, в которых классы объектов и морфизмов всё-таки являются множествами, называются малыми категориями. Далее мы будем работать только с ними.
Типы и функции
Композиция морфизмов — это композиция функций, причём синтаксис этой операции на Haskell почти идентичен математической нотации:
Рассмотрим несколько примеров типов с точки зрения теории категорий.
Множество из двух элементов — логический тип Bool :
Добавив тождественные морфизмы, получим следующую категорию:
В дальнейшем изложении будем использовать Haskell-подобную нотацию сигнатуры типов для обозначения морфизмов.
Функторы
Кроме того, должны выполняться «законы сохранения» композиции и тождественного морфизма:
Таким образом, функтор не «ломает» структуру категории: то, что было связано морфизмом в исходной категории, будет связано и в результирующей. Это верно и для крайних случаев, например, когда результирующая категория состоит из одного объекта и одного (тождественного) морфизма. Тогда все морфизмы исходной категории отобразятся в тождественный морфизм для этого объекта, но упомянутые выше законы нарушены не будут.
Посмотрим на эту картинку сильно издалека, так, чтобы сами категории превратились в точки-объекты, а функторы — в стрелки между ними (морфизмы). Получим категорию малых категорий, которая называется Cat (название периодически порождает сложные мемы с кошками).
Вернёмся к категории типов языка Haskell и будем работать с эндофункторами в этой категории. Они преобразуют типы в другие типы и, кроме того, каким-то образом преобразуют функции, работающие с этими типами.
Конструктор типа Maybe является примером такого функтора, он преобразует тип a в тип Maybe a (сам по себе Maybe не является типом!):
Монады
Все функции, которые были рассмотрены до этого, были чистыми, т.е. предполагалось, что у них нет побочных эффектов. Это функции в математическом смысле: результат чистой функции зависит только от значения её аргумента, он не меняется из-за места или времени вызова.
Поставим перед собой задачу логгировать вызовы функций. На императивном языке проще всего было бы хранить лог как глобальное состояние, которое изменяется в теле каждой функции. Программирование на функциональных языках не располагает к использованию глобального состояния, поэтому будем решать поставленную задачу, оперируя имеющимися у нас чистыми функциями — морфизмами в категории типов языка Haskell.
Типы функций позволяют составить их композицию:
Чтобы не отвлекаться на сложности реализации, в качестве представления лога возьмём просто строку. Мы хотим, чтобы после применения функции processString в логе содержалась запись «upCase toWords».
Запись в лог — побочное действие функций, мало относящееся к их основному функционалу. Хотелось бы во-первых, добавить информацию на уровне типов о том, что будет выполняться логгирование, и во-вторых, минимизировать дополнительные действия, которые придётся проделать сторонним разработчикам для работы с этими функциями.
Создадим новый тип данных, который будет помимо самих значений типа a хранить ещё и строку, в которую каждая вызванная функция будет добавлять своё имя.
Заметим, что Writer — это функтор, мы легко можем описать для него функцию fmap :
Преобразуем функции upCase и toWords и сделаем так, чтобы они возвращали значение, «завёрнутое» в тип Writer :
Теперь мы больше не можем записать композицию этих функций так же, как раньше, из-за несоответствия типов. Определим специальную функцию для композиции, которая сначала получает значение типа b и первую строку, передаёт это значение второй функции, получает значение типа c и вторую строку и в качестве финального результата возвращает значение типа c и конкатенацию строк, полученных при вычислении:
Реализация функции processString принимает вид:
Для того, чтобы получить настоящую категорию с такими морфизмами, необходимо определить ассоциативную композицию морфизмов и тождественный морфизм для каждого объекта таким образом, чтобы соблюдались аксиомы теории категорий. Тогда полученная категория называется категорией Клейсли, а функтор m — монадой. На Haskell это определение выглядит так (везде далее используются типы из категории Hask):
Например, для типа Writer реализация будет следующей:
Мы пришли к третьему определению класса Monad :
Здесь присутствует явное требование на то, чтобы m был функтором. Это ограничение не было нужно для предыдущих определений, поскольку функция fmap реализуется через >>= :
Практическое применение монад
Приведём примеры практического применения монад для решения задач, которые традиционно решаются с использованием «нечистых» функций и побочных эффектов.
Недетерминированные вычисления
Абстракция недетерминированных вычислений (т.е. таких, у которых может быть несколько возможных результатов) реализуется с помощью списков.
Тогда оператор >>= можно записать так:
Резюмируем эти реализации в классическом определении класса Monad :
Конечно, список как результат функции не обязательно обозначает недетерминированность вычислений. Хорошим примером, когда это действительно так, является реализация искусственного интеллекта для игр. Список может представлять возможные результаты хода игрока, ответных ходов может быть тоже несколько — всё время приходится работать со списками, списками списков и т.д.
Исключения
Простейшая реализация обработки исключений в чистых функциях состоит в добавлении в тип возвращаемого значения специального варианта, обозначающего, что что-то пошло не так.
Определение методов класса Monad для Maybe :
Для классификации ошибок можно использовать перечислимый тип или любую другую структуру данных, подходящую для конкретной задачи. Мы в примерах продолжим использовать просто строку. Введём синоним типа для работы с исключениями:
Композиция функций описывается аналогично случаю с использованием Maybe :
Определение экземпляра класса Monad уже не должно вызывать трудностей:
Состояния
Объявим синоним типа для работы с состоянием:
Фиксируем тип состояния s и покажем, что State s является функтором. Нам понадобится вспомогательная функция runState :
Реализация класса Functor :
Конечно, в реализации Unit можно опустить. Здесь он добавлен для того, чтобы показать эту операцию с точки зрения теории категорий.
Тип IO — один из первых, о котором узнаёт начинающий пользователь Haskell, и наверняка сразу встречает пугающее слово «монада». Такой упрощённый взгляд на этот тип как на состояние для работы с внешним миром может помочь понять, почему это так. Кончено, это описание очень поверхностно, но полноценный рассказ о том, как на самом деле реализован ввод-вывод, зависит от компилятора и выходит далеко за рамки статьи.
Монады как паттерн переиспользования кода
В предыдущей статье мы обсуждали, почему функциональное программирование это совсем не то, что распиарено, и что оно совершенно не противоречит ООП, так, что даже сам «Дядя Боб» пишет про хороший ФП дизайн порождающий хороший ООП дизайн программы (и наоборот).
Сейчас же я хочу рассказать, что такое монады на самом деле, чем они полезны для обычного практикующего разработчика, и приведу примеры, почему недостаточная поддержка их в распространенных языках приводит к копипасте и ненадежным решениям.
Но ведь в интернете буквально сотни статей про ФП и монады, зачем писать еще одну?
Дело в том, что все их (по крайней мере те что я читал) можно поделить условно на две категории: с одной стороны это статьи где вам объяснят что монада это моноид в категории эндофункторов, и что если монада T над неким топосом имеет правый сопряжённый, то категория T-алгебр над этой монадой — топос. На другой стороне располагаются статьи, где вам рассказывают, что монады — это коробки, в которых живут собачки, кошечки, и вот они из одних коробок перепрыгивают в другие, размножаются, исчезают… В итоге за горой аналогий понять что-то содержательное решительно невозможно.
Получается, что первые обычно полезны тем, кто и так знает обсуждаемую тему, а вторые даже не знаю на кого рассчитаны: сколько я их не прочитал, ничего полезного понять из них мне не удалось.
Я же хотел бы занять промежуточную позицию, и рассказать про монады без заумных терминов, но и без котиков, используя понятные ООП разработчикам термины: интерфейсы, паттерны, копипаста, инкапсуляция сложности, бойлерплейт, и так далее. В процессе работы над статьёй ни один термин теории категории использован не был.
Вступление
Итак, с чего бы начать? В нашем случае имеет место проблема курицы и яйца: чтобы мотивировать узнать про монады, я должен привести примеры их использования, но чтобы привести примеры использования, вы должны их уже знать. Поэтому я попрошу вас набраться немного терпения, и сначала узнать, что же это такое, а потом уже я обещаю показать, почему это знание полезное, и как его можно применить на практике.
Я долго думал на каком языке писать примеры, перебрал все варианты, которые знал. В итоге остановился на модифицированном C#. Scala оказалась слишком вербозной, Rust хотя и имеет концепцию трейтов, не может выразить самый простой из требуемых тайпклассов, ну а Haskell знают не все.
Но обычный сишарп не обладает нужными фичами, поэтому в статье я буду использовать синтаксис C# 10 (который еще не вышел), в частности расширение Shapes и расширение HKT. Первый из них добавляет в язык шейпы (aka тайпклассы, aka трейты). Если привести пример зачем они нужны, то вот так мы могли бы объявить тайпкласс для того, чтобы помечать классы как сериализуемые
Такой тайпкласс превратил бы рантайм эксепшн JsonSerializationException: Could not create an instance в ошибку времени компиляции. Лично я с этой ошибкой часто встречаюсь на проектах с десериализацией нетривиальных типов в кастомных форматах, поэтому и пример про него.
Второе расширение нам поможет работать с открытыми генерик-аргументами как типами. Например, это может выглядеть так:
Возможно, выглядит страшновато, но просто посмотрите на пример использования, и всё станет понятно:
Ко всему этому в статье будут ссылки на плейграунд с реализацией на актуальном C# 8. Они явно выигрывают в том, что их можно запускать, однако пользы в таком виде от них не очень много. Они приложены только для лучшего понимания написанного, потому что их можно позапускать и потыкать в дебаггере.
Что ж, прелюдия довольно ощутимо затянулась, приступим.
Functor
И первое с чего мы начнем — с функтора. «Как же так, ты же про монады рассказать обещал!» — скажете вы. Да, но функтор — базовый строительный блок многих ФП понятий, в том числе и монады, поэтому без него не обойтись.
Итак, что такое функтор? Можно долго рассуждать в терминах объектов категорий и морфизмов между ними, а можно взять наш понятийный аппарат ООП разработчиков и сказать, что Функтор — это любой объект, реализизующий тайпкласс Functor следующего вида:
Давайте подумаем какие типы из стандартной библиотеки удовлетворяют этому правилу?
Ну, самое простое, это итераторы:
Раз этот код компилируется и тест проходит, то мы доказали, что итератор в дотнете является функтором! Хотя в дотнете нет тайпклассов, тем не менее IEnumerable — это функтор, раз закон выполняется
Какой еще тип может вести себя подобным образом? Подумайте немного, вы с ним работаете каждый день по 100 раз на дню.
И конечно же это Nullable. Давайте реализуем для него тайпкласс функтора:
Таким образом мы доказали, что Nullable — это тоже функтор.
В учебниках по ФП часто упоминают про еще один закон для функторов, но тут есть один нюанс: если вы соблюдаете первый закон, то второй соблюдается автоматически. Это математический факт, так называемая «бесплатная теорема». Так что для того, чтобы проверить является ли наш класс функтором, достаточно проверить только одно простое правило, которое мы обсудили.

Map позволяет абстрагироваться от структуры контейнера, давая способ менять содержимое контейнера, ничего про эту структуру не зная
Вот мы и познакомились с одним из страшнейших зверей мира ФП — целым функтором! А дальше нас ждет ещё более сложный тайпкласс и зовут его.
Applicative
Аппликативный функтор! Который определяет не один метод, а целых два:
Что мы тут видим? Аппликативный функтор, это любой тип, который умеет:
Непонятно? Давайте разбираться. Самый простой способ разобраться в чем-то – сделать это что-то своими руками. Класс называется аппликативный функтор, в предыдущем разделе мы как раз пару функторов разобрали, возможно, они как-то связаны?
«Talk is cheap, show me the code», поэтому в качестве доказательства что наш класс является аппликативом мы, как и раньше, постараемся просто реализовать соответствующий интерфейс. Если компилятор нас не остановит — то значит мы успешно доказали то, что хотели, если же у нас в какой-то момент возникнут трудности — значит мы не правы. Давайте начнем с итератора:
Что же насчёт Nullable? Тоже никаких проблем:
Оказывается, ZipList давно существует в стандартной поставке, просто очень хорошо скрывается. Но без общего зонтичного типа Applicative он не особо полезен, поэтому дотнет обходится просто одинокой функцией Zip.
С одной стороны, функция простая, можно даже сказать скучная. А с другой — посмотрите, мы написали очень абстрактную функцию Combine, которая совершенно ничего не знает о переданных значениях, но при этом умеет производить очень сильно различающиеся действия. Для двух списков она считает комбинаторику всех пар, для нуллейблов оно возвращает либо пару элементов, если оба переданных параметра имели значение, либо null. Для ZipList мы сцепили соответствующие элементы двух списков, причем результирующий список был усечен до самого короткого из двух. Таким образом, аппликатив позволяет нам разделить действие над элементами контейнера (это наша функция (a, b) => (a, b) ) и форму контейнера (это T<> ). То есть, с одной стороны, мы можем описывать вычисления, не заботясь о форме контейнера (опциональное значение/список/промис/что угодно), а с другой мы, наоборот, можем реализовать некий контейнер, а варианты работы с этим контейнером оставить на откуп клиентскому коду.
Остаётся добавить, что еще есть всякие законы, которые должны выполняться, но они достаточно очевидны, вроде ассоциативности операций и так далее. Чтобы не раздувать текст статьи я их доказывать не буду, потому что, по сути, эти законы просто проверяют соблюдение «Принципа наименьшего удивления». Можно почитать про них по ссылке и удостовериться, что они накладывают достаточно ожидаемые ограничения.

pure позволяет нам создать контейнер, содержащее единственное значение

liftA2 позволяет нам использовать функцию от двух аргументов, имея на руках
два контейнера с соответствующими типами, упакованными внутри
Прежде, чем мы приступим к герою сегодняшнего дня, хочу обратить внимание, что тайпкласс который мы только что обсудили называется «Аппликативный функтор». Почему именно так? «Аппликативный» означает что с ним мы можем применять упакованные функции к упакованным значениям. Например, у нас может быть список функций, и список значений. Применив к ним LiftA2 мы получим список результатов каждой функции примененной к каждому значению. Ну, это нужно бывает не часто, а вот из двух опциональных значений сделать третье, если в обоих не null — буквально каждый день. Или выполнить две асинхронные операции и вычислить на их основании какой-то ответ.
А почему функтор? Имея функции LiftA2 и Pure легко реализовать Map :
Ссылка на плейграунд. Можно убедиться, что поведение такое же, какое было изначально.
Также легко реализовать тайплкасс аппликатива для Task :
Monad
И вот он. Тайпкласс, одним своим названием повергающий в ужас. И который состоит
из целых двух функций, одну из которых мы уже знаем:
Если говорить по-русски, то:
Таким образом монада — это простейший интерфейс, который тривиально реализовать для того же итератора, что мы в очередной раз и сделаем:

Монады позволяют имея на руках контейнер с элементами типа А и функцией из А в такой же контейнер типа В получить контейнер типа В
Кроме того, что монады чрезвычайно просты, они еще и настолько полезны, что захардкожены в большинстве языков. Думаю, многим хабровчанам известно, что в хаскелле и скале есть так называемая do-нотация. Она рассахаривает такой хаскель код:
в последовательность вызовов функции Bind которую мы только что разобрали:
Как видите, это одна простая конструкция, которая работает по одному паттерну.
А что у нас в сишарпе? А в нём есть аж целых три его захардкоженных вариации. Например, что это за код?
Это ни что иное, как do-нотация для монады итератора (в хаскелле итератор называется списком):
Давайте теперь посмотрим на такой код:
А это do-нотация для монады Maybe (она же Option, она же с некоторой натяжкой — Nullable):
Что насчет вот такого кода?
А это do-нотация для монады IO (про которую мы не говорили, но, по сути, это просто аналог Task из сишарпа):
На этой ноте предлагаю перейти к первому пункту обещанного параграфа под названием.
Зачем нам монады
Упрощение синтаксиса языка
Первым пунктом, следующим из предыдущего абзаца, стоит выделить упрощение языка. Посмотрите, сколько мусора натащил сишарп, чтобы выразить простую идею «Сделай что-нибудь, а затем сделай что-нибудь еще». И асинк-авейт, и LINQ, и null propagation являются частными случаями общей идеи. Причем которые очень часто ломаются на ровном месте. Захотел вызвать статический метод на nullable-параметре? Всё, элвис-оператор использовать не получится, пиши, как в старые-добрые времена проверку на нулл. Захотел заавейтиться внутри лямбды? Тебе компилятор скажет всё, что он думает об этой затее. Ну, хоть в случае списка, ломаться особо нечему, за исключением уродливых скобочек если нужно сделать хоть что-то выходящее за рамки LINQ-синтаксиса (например, вызвать First в конце запроса).
А в другом углу ринга у нас do-нотация, которая выглядит абсолютно одинаково во всех случаях, которая позволяет всё, что позволяет родная монада, и которая состоит всего из одного ключевого слова, вместо россыпи операторов и кейвордов в случаях других языков.
И главное: при этом она базируется на интерфейсах, а не на захардкоженных в компиляторе эвристиках преобразования кода в стейт-машины. На интерфейсах, которые позволяет разработчику не ждать годами, пока команда языка соблаговолит наконец реализовать комбинатор пары монад, и которые не требуют костылить в язык кучу хаков. Что насчёт асинк энумерейбла, который автоматически параллелит получение данных по сети (мы не обсуждали, но в хаскелле для параллелизации есть монада Par )? Ну, пока ничего, ждем C# 15, в котором, возможно, это появится. А может и не появится.
Упрощение стандартной библиотеки языка
А по факту что мы имеем? Абсолютно ужасную копи-пасту в стандартной библиотеке. Вот в версии 1.29 появляется flatten для итератора, а вот спустя более чем год он же, но для опшна. Для футур он живет в стороннем крейте, который надо подключать.
Вот год назад появился transpose для Option/Result друг в друга, при том, что transpose из итератора для них появился аж в версии 0.8 в 2013 году. transpose для футур (которые как мы помним реализация IO монады для раста) до сих пор нет, еще 7 лет подождем, и они появятся.
Продолжать можно ещё долго, но суть остается прежней: можно было реализовать Monad трейт один раз, и дальше эти transpose/flatten/. появлялись бы во всех совместимых типах автоматически. Да, для конкретных классов реализация по-умолчанию может быть не оптимальной, но ведь всегда можно выполнить специализацию, особенно в стандартной библиотеке. В итоге имеется огромная проблема, которой в языке от 2015 года вообще не должно было быть изначально. Но, монад нет, и починить это в текущей версии языка невозможно, остается только копипастить однотипные реализации из типа в тип.
Однако, не стандартной библиотекой единой живы, и наш следующий пункт
Сторонние библиотеки
Благодаря тому, что тайпкласс Monad (да и в целом тайпклассы) чрезвычайно абстрактный, можно создавать совершенно потрясающие удобные библиотеки. Например, возможно, вы помните мою статью, где я попробовал написать простенькое приложение на хаскелле и на го. В комментариях мне справделиво указали на то, что сравнение было «нечестным» — в го я старательно писал всё с нуля, в процессе чего я собственно несколько раз и ошибся, а в хаскелле я взял пару библиотек (для работы с деревьями и последовательностями), и написал только пару строчек, которая их склеивает вместе, где ошибиться было просто негде, ну оно и заработало как надо.
Но в тех же комментариях один из хабровчан дал замечательный ответ, который объясняет, что вовсе не случайно в хаскеле такие библиотеки есть, а в Go нет. Именно возможность спрятать конкретные реализации за тайпклассами Functor/Applicative/Monad/… и позволяет таким библиотекам существовать. Нет тайпклассов и HKT — не будет крутых библиотек, зато нужны будут разработчики, которые на зарплате будут копипастить реализации для новых конкретных монад, буде условному майкрософту или мозилле вздумается добавить их в язык. И, в отличие от общего решения, они будут это делать для тех кейсов, которые сочтут достойными. Если ваша монада не такая популярная, как список или опциональное значение, то останетесь без удобного способа смоделировать предметную область.
Для опытных шарпистов, кстати, это вовсе не новость. Например, есть куча полезных библиотек, на базе IEnumerable. Не будь такого интерфейса — не было бы и их. Куча удобных ORM в сишарпе основанна на IQueryable, который является такой специализированной монадой списка для БД, и без которого я думаю ситуация с ORM в сишарпе была бы куда печальнее. Именно подобные абстракции дают возможность творить по-настоящему мощные библитеки, и если даже на единственной монаде списка мы можем делать такое, то чего мы можем достичь с их совокупной мощью? А если мы еще и комбинировать их будем?
Хотел заметить, что абстрактный — не значит сложный, а скорее наоборот. Как известно — любую проблему в программировании можно решить еще одним уровнем абстракции, кроме слишком большого количества уровней абстракции. Поэтому, когда я говорю «смотрите какая абстрактная мощь», я говорю про то, что эта мощь позволяет просто рассуждать о сложных процессах, а не просто никому не нужная акробатика на типах. Абстракции — упрощают программирование, а не усложняют.
Да, нужно изучить, какие бывают тайпклассы и что они умеют, хотя не так уж это и страшно: мы в статье рассмотрели где-то треть основных. Но потом этим знанием можно пользоваться до конца жизни. Посмотрите на объем документации Akka, там её действительно очень много. Но теперь спросите у людей, которые на ней пишут — хотели бы они сами с нуля реализовывать весь функционал, который в ней есть? Да, верю, что многие разработчики пожурят что они-то дескать лучше бы сами все сделали, и было бы их решение простое, красивое, да еще и производительное как у гугла. Но вот только велика вероятность что они лукавят, и если у них на проекте используется и персистентность, и автобалансировка акторов, и гарантированная доставка, и какие-нибудь другие нетривиальны фичи, то куда проще разобраться один раз в документации и настроить всю машинерию, чем сделать что-то подобное с нуля. Потому что умные люди написали удобную абстракцию, и работать с ней куда проще, чем делать такое самому. Это правда, что чем сложнее система типов, тем более инопланетную фигню можно навертеть, но так же верно и то, что некоторые вещи просто невозможно сделать удобно в более слабых системах типов.
Поэтому я считаю, что будущее именно за мощными языками, позволяющими делать удобные библиотеки, а не за кодом, который быстро написал — быстро выбросил и сделал новый. Такой подход работает, да, но по-моему опыту на проектах не больше пары сотен строк кода, как только их стало больше — лучше с библиотеками, которые кто-то написал, и хорошо бы, чтобы они были достаточно абстрактными и удобными, чтобы их можно было взять и использовать. Плюс монады — вещь стандартизованная, с простым интерфейсом, и что немаловажно — предсказуемыми свойствами, а гениальные архитектурные решения в каждой компании — свои уникальные, и последствия от их использования бывают самые разные.
Выразительность
Тайпкласс монады позволяет очень четко выражать намерения в коде. К слову, пример того, как хорошо дружит ООП с ФП: монады позволяют удобно и красиво следовать четвертому принципу SOLID. Каким образом? А таким, что код, написанный с использованием монад, выглядит подобным образом:
Причем, таким образом с монадами мы одновременно следуем и последней букве SOLID, решая одну из самых больших головных болей в ООП разработке — инверсию зависимостей. Нам не нужны гигантские Autofac/Windsor/Ninject/… которые падают в рантайме «нишмагла найти зависимость», вы просто описываете в обычных where условиях нужный функционал, и если вы забыли передать зависимость, то компилятор вам об этом напомнит. Вам не нужна магия, внешняя по отношению к языку, вы просто пишете на сишарпе, а компилятор вам поможет.
Тестируемость
Частично связанное с предыдущим пунктом, абстрагированность от некоторых особенностей логики вроде того, является ли функция асинхронной, позволяет избавиться от моков.
Один из примеров, как ФП помогает избавиться от моков, я демонстрировал в предыдущей статье, на примере заказа кофе в кофейне. Другой пример можно привести такой: допустим, мы написали типичный код, который по сети достает какие-то данные и как-то их преобразует.
Теперь мы хотим этот код протестировать. Что мы обычно делаем в C# в таком случае?
Ну, хорошим стилем в сишарпе считается делать тестируемые типы, поэтому наш MyService принимает remoteClient в виде аргумента конструктора, который мы и будем мокать.
А что нам даёт механизм с монадами? Предлагаю вашему внимание простейшую, и бесполезную (но только на первый взгляд) монаду Id, которая просто оборачивает своё значение и больше ничего не делает:
Теперь вместо функции:
С do-нотацией было бы вообще 1к1, но и так сойдет. Соответственно в нашем бизнесовом коде будет:
А в коде с тестами:
И никаких моков асинхронного взаимодействия! Потому что мы сделали ту самую инверсию контроля, про которую говорит SOLID (и снова нам в этом помогли практики ФП). Раньше вызываемый код решал сам, что он хочет запустить асинхронную операцию, что приводило к головной боли у вызывающего, которому приходилось давать фейковое асинхронное взаимодействие. Но оказалось, что это знание лишнее. Наша функция всего лишь хотела сделать операцию, а когда получит её результат сделать что-то еще. И в очередной раз мы сталкиваемся с тем, что нам для этого нужен просто монадический интерфейс. То есть функция ошибочно накладывает слишком много ограничений на вызывающего. Изолировав это знание в бизнесовом коде мы получили возможность на своей стороне решать, в каком виде мы хотим иметь результат.
Как следствие — у нас очень сильно упрощается код. Не нужно писать моки, не нужно лепить бесконечные Task.FromResult из-за того что интерфейс асинхронный. Можно просто писать бизнесовую логику, и на месте решать, какой эффект мы хотим. Причем это работает не только для тестов: мы можем написать общий интерфейс с двумя реалзиациями: синхронной и асинхронной, и использовать подходящий. Прощай вопросы вроде «должен ли я делать асинхронные врапперы над синхронными функциями», или может наоборот. Просто пишите в контексте монады, а дальше вызывающий код решит, как вас использовать.
Заключение
Если честно, я даже не думал, что получится так много текста. Первоначально я планировал рассказать и про Traversable, и Foldable, и как они помогли решить ту задачу с деревьями, но сейчас я понимаю, что уже полностью исчерпал лимит внимательности у вас, как читателей.
Давайте подытожим, какие в итоге существуют основные тайпклассы и что они умеют:
Функтор (ооп. Mappable)
Что такое: это любой класс, реализующий функцию Map определенной сигнатуры, для которой выполняется одно простое правило.
Пример: преобразование итератора одних значений в итератор других значений;
преобразование результата асинхронной операции
Аппликативный функтор (Аппликатив, ооп. PairMappable)
Монада (ооп. NestedJoinMappable):
Что такое: это любой класс, реализующий пару функций Pure и Bind (и опять правила).
Реализация этих методов гарантирует автоматическую реализацию тайпкласса «Аппликатив».
Пример: выполнение нескольких асинхронных операций, зависящих друг от друга; парсинг языка с контекстно-зависимой грамматикой
Надеюсь, я смог показать, что монады (и остальные упомянутые в статье тайпклассы) это не какие-то страшные монстрозвери, которые не дают спать, а
К сожалению, одну статью физически невозможно невозможно уместить все возможные применения, поэтому я предлагаю просто потыкать их самостоятельно, и убедиться самому, что эта концепция действительно выручает во многих случаях.