Что такое момент силы трения
Общие сведения
Во время перекатывания тел возникает их взаимодействие. Описывается оно силой трения качения. Её существование возможно только при контакте поверхностей. При этом наряду с качением возникают силы покоя и скольжения. Объект, катящийся по другому телу, испытывает только трение, вызванное качением. По сравнению с другими силами оно небольшое, но при этом помогает осуществлять перемещение.
С физической точки зрения, трение представляет собой вектор, направление которого совпадает с линией, проходящей вдоль касательной трущихся поверхностей. Сила, измеряемая относительно перемещения соприкасающихся тел, называется внешней, а возникающая в области одного объекта, например, газа — внутренней.
Трение зависит от поверхности тел. Оно может быть сухим или вязким. В единицах СИ сила измеряется в ньютонах: [P]=H. Существует такое понятие, как адгезия, то есть способность тел «прилипать» друг к другу. Зависит она от шероховатости. Чем этот параметр больше, тем больше нужно затратить энергии для смещения поверхностей, но в то же время её затраты будут меньше для полного торможения.
Таким образом, трение может приносить как пользу, так и вред. С одной стороны, при работе за счёт силы происходит износ поверхностей, а с другой — выполняется торможение. Для уменьшения эффекта существуют несколько способов изменить трение: сгладить поверхности, сменить смазку, заменить скольжение качением.
Вычисление силы выполняют по формуле: F = k * N. Здесь:
Приложенное сопротивление направлено в противоположную сторону движения, при этом реакция силы опоры происходит перпендикулярно площади соприкосновения. Коэффициент является безразмерной величиной и не зависит от размера контакта. Если энергия движения совпадает по величине с трением, тело движется равномерно по прямой. Если же движущая сила будет меньше, объект остановится.
Основная формула силы трения учитывает различные моменты, оказывающие влияние на перемещение. Но при этом, если при соприкосновении с вращением не будет проскальзывания, формула изменится. В ней главную роль будет играть прижимающее давление.
Качение тела
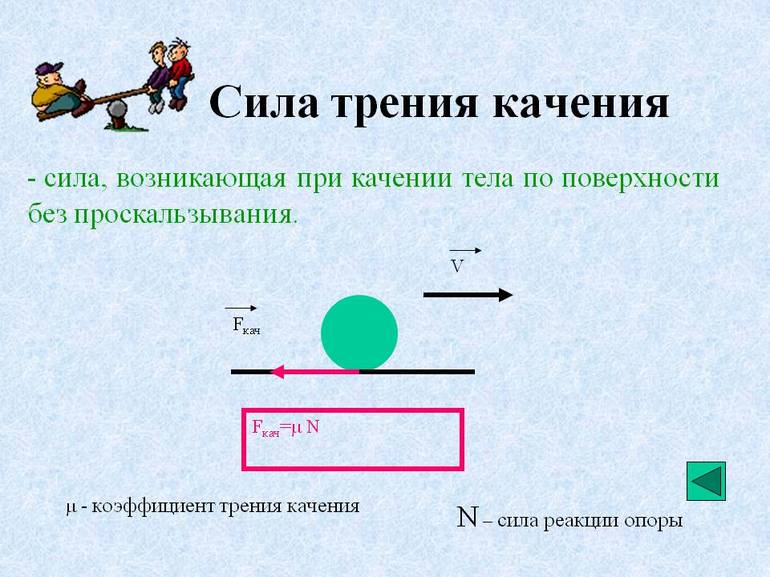
Из названия силы можно сделать вывод, что сила качения возникает, когда одно тело перекатывается по поверхности другого. Например, езда с использованием колеса, работа подшипника. По сути, это явление, происходящее из-за деформации катка и опорной поверхности. При этом полагается, что тяговых и тормозных процессов нет.
Из-за того, что трение качения в несколько раз меньше скольжения, оно является довольно распространённым видом перемещения. Например, груз катить легче, чем тянуть. Это происходит из-за меньшего количества контактов с поверхностью. При этом отталкиваться от твёрдого тела проще, чем от мягкого.
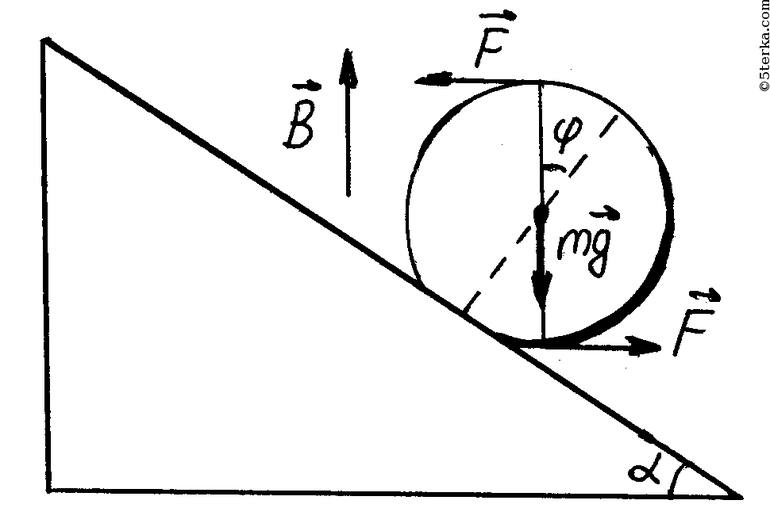
Для определения процесса физики используют следующее объяснение: пусть имеется тело, которое располагается на опоре. Относительно неё происходит вращение. В любой выбранный момент времени на вращающийся объект будет действовать момент сил. При этом векторная сумма их будет равняться нулю: N + P +Ro = 0. Действующий момент состоит из внешней силы (P), прижимной (N) и реакции опоры (Ro).
Если сумма векторов равняется нулю, ось симметрии находится в равномерном и прямолинейном движении или остаётся в одном положении (неподвижная). Другими словами, вектор силы трения качения противодействует перемещению. Следовательно, прижимной момент уравновешивается реакцией опоры, а, точнее, её вертикальной составляющей. Внешняя же сила находится в равновесии с горизонтальной составляющей.
Равномерность обозначает, что воздействующие моменты компенсируют друг друга. А значит, формула для описания процесса будет выглядеть как Ft * R = N * f, где Ft — сила трения качения. Из этой формулы можно найти силу: Ft = f * N /R. Рассматриваемое воздействие прямо пропорционально произведению коэффициента трения и прижимной силы, обратно пропорционально радиусу катящегося тела. Фактически это и есть определение трения качения.
Правильность формулы подтверждают различные экспериментальные измерения. Действительно, при малой скорости качения процесс не зависит от неё. Когда же скорость возрастает до величин сопоставимых с деформацией в опоре, сопротивление движению становится пропорциональным её росту и влияние оказывает уже скольжение.
Момент и коэффициент
Пусть имеется цилиндр, расположенный на идеальной гладкой жёсткой поверхности. Какую бы силу Q ни приложили, уравновесить её можно только противодействующей энергией. Если же такой энергии нет, под действием Q цилиндр должен катиться. Но опыты показывают совершенно другое. Например, если подойти к многотонному грузовику и попробовать его толкнуть, он не покатится. Хотя теория утверждает обратное.
Но здесь дело в том, что поверхность считается идеальной. В момент времени на тело, кроме Q, действует равное ей сцепление. Эти силы будут уравновешенными. В вертикальной же плоскости на тело действует нормаль (N) и противодействующая ей сила равновесия (P).
На самом деле при прикосновении тело деформируется. Образуется впадина, при этом колесо всей своей тяжестью будет опираться на крайнюю правую точку деформированной поверхности. Момент сил здесь будет следующим:
Перемещению препятствует равновесие пары PN. При этом плечо пары будет половиной размера, то есть возникает момент сил трения. Определяют его как эн делённое на дельту и называют моментом трения: Mтр = N * d. Эта формула совпадает по форме записи с законом Амонтона — Кулона. И там, и тут фигурирует величина опоры.
Становится очевидным, что R * Q = Mтр = P * d. Используя эту запись, можно обнаружить предельный импульс, который необходимо приложить к колесу, чтобы заставить его двигаться: Q = p d /R. При этом если колесо будет скользить, а не катиться, Q будет уже зависеть от трения: Q = P * f.
При сравнении двух формул видно, что d / r будет намного меньше f, поэтому качение произойдёт раньше. Это свойство как раз и используется в подшипниках. Нахождение коэффициента трения можно выполнить через момент трения качения и давление прижима: f = Mтр / N.
Он определяется следующими физическими интерпретациями:
Для мягкого дерева, катящегося по стали, коэффициент составляет 0,8 мм, стали по асфальту — 6 мм, железа по граниту — 2,1 мм. Это справочная величина, установленная экспериментально, которую не нужно вычислять самостоятельно.
Решение задач
При решении задач нужно помнить, что трение кручения зависит не только от свойств материалов, участвующих в движении, но и от радиуса. При этом часто областью деформации пренебрегают, так как величина смятия ничтожно мала, поэтому нахождение по формуле силы трения через массу при качении не выполняют.
Алгоритм решения примеров:
Например, имеются 2 цилиндра с одинаковыми радиусами: R = 50 см. Их вес составляет соответственно 20 и 30 ньютон. Они соединены стержнем массой 40 ньютон. Первый цилиндр катится без сопротивления, а второй испытывает трение d = 2 мм. К первому кольцу приложена пара моментов, а к оси второго — нагрузка в 10 ньютон. Определить пределы изменения момента в условиях равновесия.
Для решения задачи нужно воспользоваться формулой: Мтр = N2 * d. Систему можно разбить на 3 тела. Связи заменить реакциями Fc1, N1, Fc2, N2. Внутренние связи обозначить x1, y1, x2, y2. При составлении системы нужно избегать уравнений с реакциями F. Равновесие для первого цилиндра можно определить из системы:
Для второго колеса:
Для стержня:
Из решения системы можно определить, что М = (√3R FR √2 — d (G3 + 2G2 + FV2)) / (R (√3+d)). Все вычисления нужно делать в метрах. Подставив значения, заданные условием, можно вычислить, что М = 3,414. Нормальные реакции будут равны: N = 36,058 Н, N2 = 61,013 Н. Аналогичные вычисления выполняют и при изменении направления возможного перемещения. В ответе должно получиться, что M = 3, 66 Нм, N1 = 35.8 Н, Т2 = 61,3 Н. Таким образом, предел будет лежать в области от 3,414 Нм до 3, 66 Нм.
Как определить момент сил трения?
Когда решают любые задачи по физике, в которых имеются движущиеся объекты, то всегда говорят о силах трения. Их либо учитывают, либо ими пренебрегают, но факт их присутствия ни у кого не вызывает сомнения. В данной статье рассмотрим, что такое момент сил трения, а также приведем проблемы, для устранения которых воспользуемся полученными знаниями.
Сила трения и ее природа
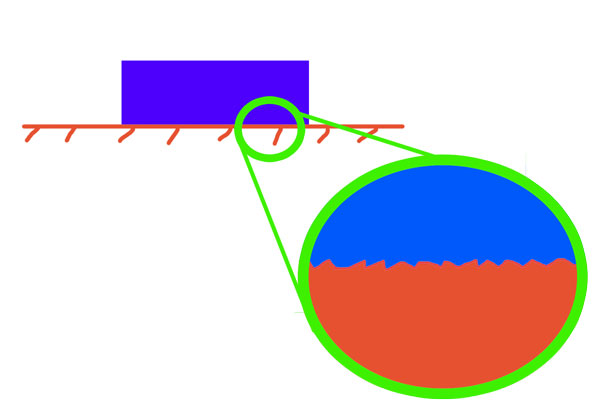
Каждый понимает, что если одно тело движется по поверхности другого совершенно любым способом (скользит, катится), то всегда существует некоторая сила, которая препятствует этому перемещению. Она называется динамической силой трения. Причина ее возникновения связана с тем фактом, что любые тела имеют микроскопические шероховатости на своих поверхностях. Когда соприкасаются два объекта, то их шероховатости начинают взаимодействовать друг с другом. Это взаимодействие носит как механический характер (пик попадает во впадину), так и происходит на уровне атомов (дипольные притяжения, ван-дер-ваальсовые и другие).

Когда соприкасаемые тела находятся в покое, то, чтобы привести их в движение относительно друг друга, необходимо приложить усилие, которое больше такового для поддержания скольжения этих тел друг по другу с постоянной скоростью. Поэтому помимо динамической также рассматривают статическую силу трения.
Свойства силы трения и формулы для ее вычисления

В школьном курсе физики говорится, что впервые законы трения изложил французский физик Гийом Амонтон в XVII веке. На самом деле это явление стал изучать еще в конце XV века Леонардо да Винчи, рассматривая движущийся предмет по гладкой поверхности.
Свойства трения могут быть кратко изложены следующим образом:
Эти особенности рассматриваемого явления позволяют ввести следующую математическую формулу для силы трения:
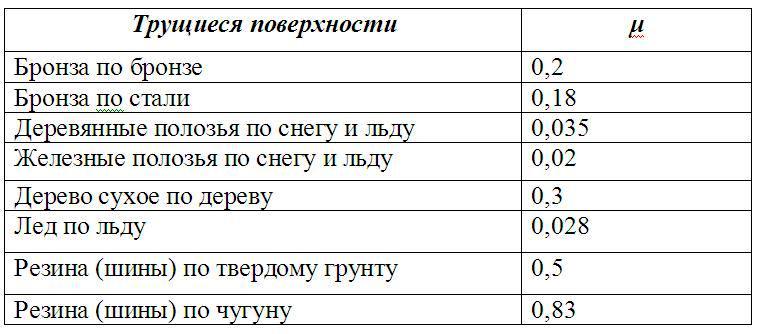
Значение коэффициента μ зависит исключительно от свойств поверхностей, которые трутся друг о друга. Таблица значений для некоторых поверхностей приведена ниже.
Для трения покоя формула используется та же самая, что приведена выше, однако значения коэффициентов μ для тех же поверхностей будут совершенно иные (они больше по величине, чем для скольжения).
Особый случай представляет трение качения, когда одно тело катится (не скользит) по поверхности другого. Для силы в этом случае применяют формулу:
Момент силы
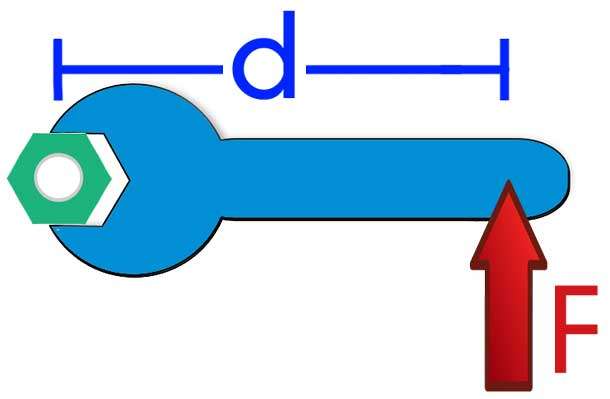
Перед тем как отвечать на вопрос, как определить момент сил трения, необходимо рассмотреть само физическое понятие. Под моментом силы M понимают физическую величину, которая определяется как произведение плеча на значение силы F, приложенной к нему. Ниже приведен рисунок.
Здесь мы видим, что приложение F к плечу d, которое равно длине гаечного ключа, создает крутящий момент, приводящий к откручиванию зеленой гайки.
Таким образом, для момента силы справедлива формула:
Заметим, что природа силы F не имеет никакого значения: она может быть электрической, гравитационной или вызванной трением. То есть определение момента силы трения будет тем же самым, что приведено в начале пункта, и записанная формула для M остается справедливой.
Когда появляется момент сил, вызванный трением?
Эта ситуация возникает, когда выполняются три главных условия:
Как найти момент силы трения?
Чтобы решить эту задачу, необходимо сначала определить, на какие вращающиеся элементы действует сила трения. Затем следует найти расстояние от этих элементов до оси вращения и определить, чему равна сила трения, действующая на каждый элемент. После этого необходимо выполнить умножение расстояний ri на соответствующие величины Fi и сложить полученные результаты. В итоге суммарный момент сил трения вращения вычисляется по формуле:
Далее решим две задачи, где используем рассмотренные формулы.
Вращение диска болгарки
Известно, что когда диск болгарки радиусом 5 см режет металл, то он вращается с постоянной скоростью. Необходимо определить, какой момент сил создает электромотор прибора, если сила трения о металл диска равна 0,5 кН.
Поскольку диск вращается с постоянной скоростью, то сумма всех моментов сил, которые на него действуют, равна нулю. В данном случае мы имеем всего 2 момента: от электромотора и от силы трения. Поскольку они действуют в разных направлениях, то можно записать формулу:
Поскольку трение действует только в точке соприкосновения диска болгарки с металлом, то есть на расстоянии r от оси вращения, то ее момент силы равен:
M2 = r*F=5*10-2*500 = 25 Н*м.
Поскольку электромотор создает такой же по модулю момент, получаем ответ: 25 Н*м.
Качение деревянного диска
Имеется диск из дерева, его радиус r равен 0,5 метра. Этот диск начинают катить по деревянной поверхности. Необходимо рассчитать, какое расстояние способен он преодолеть, если начальная скорость вращения его ω составляла 5 рад/с.
Кинетическая энергия вращающегося тела равна:
Момент инерции диска I равен m*r2/2. Чтобы вычислить момент M силы трения F, следует заметить, что она действует вдоль края диска в точке его соприкосновения с деревянной поверхностью, то есть M = r*F. В свою очередь F = f*mg/r (сила реакции опоры N равна весу диска mg). Подставляя все эти формулы в последнее равенство, получим:
m*r2*ω2/4 = r*f*mg/r*θ => θ=r2*ω2/(4*f*g).
Поскольку пройденное диском расстояние L связано с углом θ выражением L=r*θ, то получаем конечное равенство:
Значение f можно посмотреть в таблице для коэффициентов трения качения. Для пары дерево-дерево он равен 1,5*10-3 м. Подставляем все величины, получаем:
L=0,53*52/(4*1,5*10-3*9,81) ≈ 53,1 м.
Для подтверждения правильности полученной конечной формулы можно проверить, что получаются единицы измерения длины.
ОПРЕДЕЛЕНИЕ МОМЕНТА СИЛ ТРЕНИЯ И МОМЕНТА ИНЕРЦИИ МАХОВОГО КОЛЕСА.



ОПРЕДЕЛЕНИЕ МОМЕНТА СИЛ ТРЕНИЯ И МОМЕНТА ИНЕРЦИИ МАХОВОГО КОЛЕСА.
Методические указания к лабораторной работе №13 по физике
Составители: Т.П. Жданова, В.В. Илясов, А.П. Кудря, В.С. Кунаков
Указания содержат краткое описание рабочей установки и методики определения момента инерции махового колеса.
Методические указания предназначены для студентов инженерных специальностей всех форм обучения при выполнении лабораторного практикума по физике (раздел «Механика и молекулярная физика»).
Печатается по решению методической комиссии факультета
«Нанотехнологии и композиционные материалы»
Научный редактор проф., д.т.н. В.С. Кунаков
© Издательский центр ДГТУ, 2009
Лабораторная работа №13
ОПРЕДЕЛЕНИЕ МОМЕНТА СИЛ ТРЕНИЯ И МОМЕНТА ИНЕРЦИИ МАХОВОГО КОЛЕСА.
Цель работы: Определение момента сил трения, момента инерции махового колеса и сравнение его с теоретическим расчётом.
Оборудование: экспериментальная установка, секундомер,
1. Теоретическая часть.
При изучении вращательного движения твердого тела используют понятие момента инерции. Моментом инерции твердого тела (либо системы тел) относительно некоторой оси называется физическая величина, равная сумме произведения масс материальных точек системы на квадрат их расстояний до оси вращения: 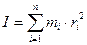
где 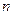
В случае непрерывного распределения масс момент инерции может быть определен интегралом: 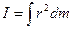
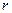
Момент инерции зависит от массы тела и формы распределения массы относительно оси вращения.
Момент сил – физическая величина, определяемая векторным произведением радиуса-вектора 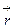
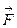
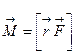
где 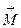
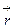
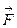
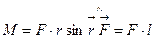
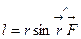
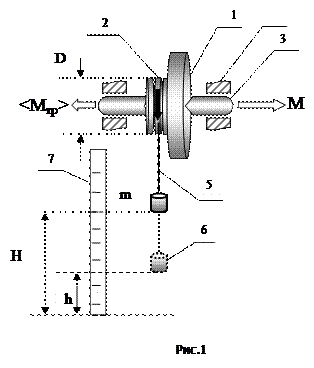
2. Описание экспериментальной установки. Вывод формул для определения момента сил трения и момента инерции махового колеса
Измерительная установка состоит из махового колеса (диска) 1 со шкивом 2, насаженного на вал 3, установленный на шарикоподшипниках 4. На шкив наматывается эластичная нить 5, к концу которой крепится груз 6, масса которого заданна. Положение груза фиксируют по отсчетной линейке 7.
1) Если груз массы 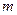
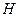
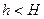
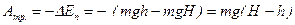
Средний момент сил трения обусловлен трением оси в подшипниках, махового колеса о воздух. Потерей энергии на деформацию нити и трение груза о воздух пренебрегаем.
Работа среднего момента сил трения можно выразить через угловое перемещение колеса 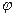
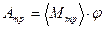
Угловое перемещение 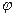
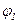
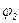
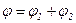
Угловое перемещение колеса 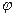
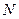
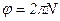
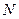
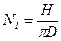
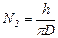
С учетом (4) 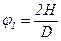
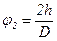
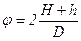
Подставим (5) в (2) получим
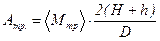
Из (1) и (6) получаем выражение для вычисления момента сил трения:
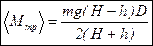
2) Если груз из верхней точки опускается в нижнюю, то потенциальная энергия груза ( 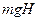
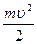
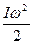
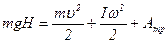
Работа среднего момента сил трения:
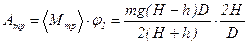
С учетом (9), уравнение (8) примет вид:
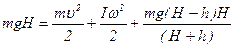
Учитывая, что линейная скорость движения груза 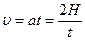
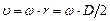
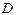
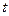
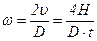
Совместное решение (10) и (11) позволяет определить момент инерции махового колеса:
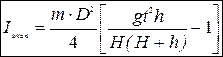
3. Порядок выполнения лабораторной работы:
ЗАДАНИЕ 1. Определение среднего момента сил трения и момента инерции махового колеса.
1. Занести в таблицу 1 все известные величины и их абсолютные погрешности, указанные на установке: 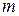
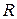
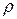
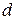
2. С помощью штангенциркуля измерить диаметр шкива 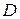
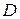
3. Включить в сеть шнур питания секундомера. Нажать на кнопку «сеть», расположенную на лицевой панели секундомера.
4. Вращая маховое колесо, зафиксировать груз в верхнем положении на высоте 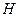
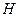
5. Нажать кнопку «сброс» и убедиться, что на табло установлены нули.
6. Груз отпустить и одновременно нажать кнопку «пуск» на секундомере, секундомер начинает отсчёт времени, а в момент пересечения грузом нижнего положения нажать кнопку «стоп».
7. Произвести отсчёт времени хода груза 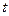
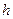
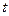
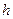
8. Вычислить по формуле (7) средний момент сил трения (для среднего значения 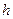
9. Вычислить по формуле (12) момент инерции махового колеса 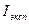
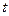
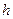
10. Результаты вычислений по формулам (7) и (12) занести в таблицу 3.
11. Произвести статистическую обработку результатов измерения времени 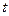
12. Вычислить относительные и абсолютные погрешности по формулам (13) – (16) и занести в таблицу 3:
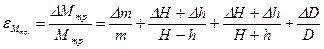
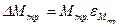
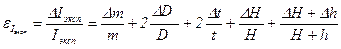
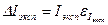
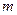 | 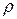 | 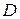 | 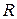 | 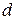 | 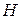 | |
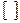 | 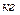 | 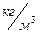 | 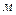 | 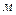 | 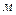 | 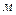 |
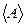 | ||||||
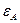 | ||||||
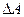 |
| № п/п | 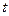 | 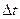 | 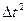 | 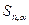 | 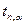 | 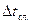 | 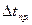 | 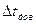 | 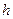 | 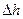 |
| с | с | с 2 | с | — | с | с | с | 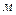 | 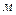 | |
| Ср. |
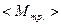 | 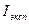 | 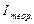 | 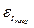 | |
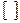 | 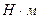 | 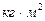 | 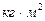 | 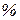 |
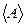 | ||||
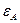 | ||||
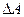 |
ЗАДАНИЕ 2. Теоретический расчёт момента инерции махового колеса.
1. Момент инерции махового колеса 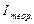
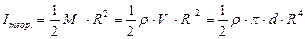
Моменты инерции шкива и вала не учитываем.
Рассчитать относительную погрешность по формуле 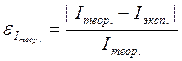
Результат занести в таблицу 3.
2. Сравнить теоретическое и экспериментальное значения момента инерции и объяснить результат. Сделать вывод.
Контрольные вопросы
1. Что называется моментом инерции материальной точки?
2. Что называется моментом инерции твёрдого тела? От чего он зависит?
4. Момент инерции тел простейшей формы относительно оси, проходящей через центр инерции. Физический смысл момента инерции.
5. Вывести формулу для определения среднего момента сил трения.
6. Вывести формулу для определения момента инерции махового колеса.
7. Записать основной закон динамики вращательного движения.
8. Теорема Штейнера.
9. Чем обусловлен момент сил трения в данной работе?
Рекомендуемая литература
1. Савельев И.В. Курс общей физики (т.1). М.: Наука, СПб.: Лань, 2006.
2. Трофимова Т.И. Курс физики. М.: Высш. Шк., 2004.
Составители: Т.П. Жданова, В.В. Илясов, А.П. Кудря, В.С. Кунаков