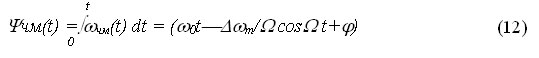Что такое модуляция радиосигнала

Урок 2.2 Радиосигналы, передача информации, модуляция

В Уроке 2.1 была рассмотрена тема о радиоволнах и распределении частот в эфире. В этом уроке попытаемся выяснить в простой и доступной форме как это реализуется практически.

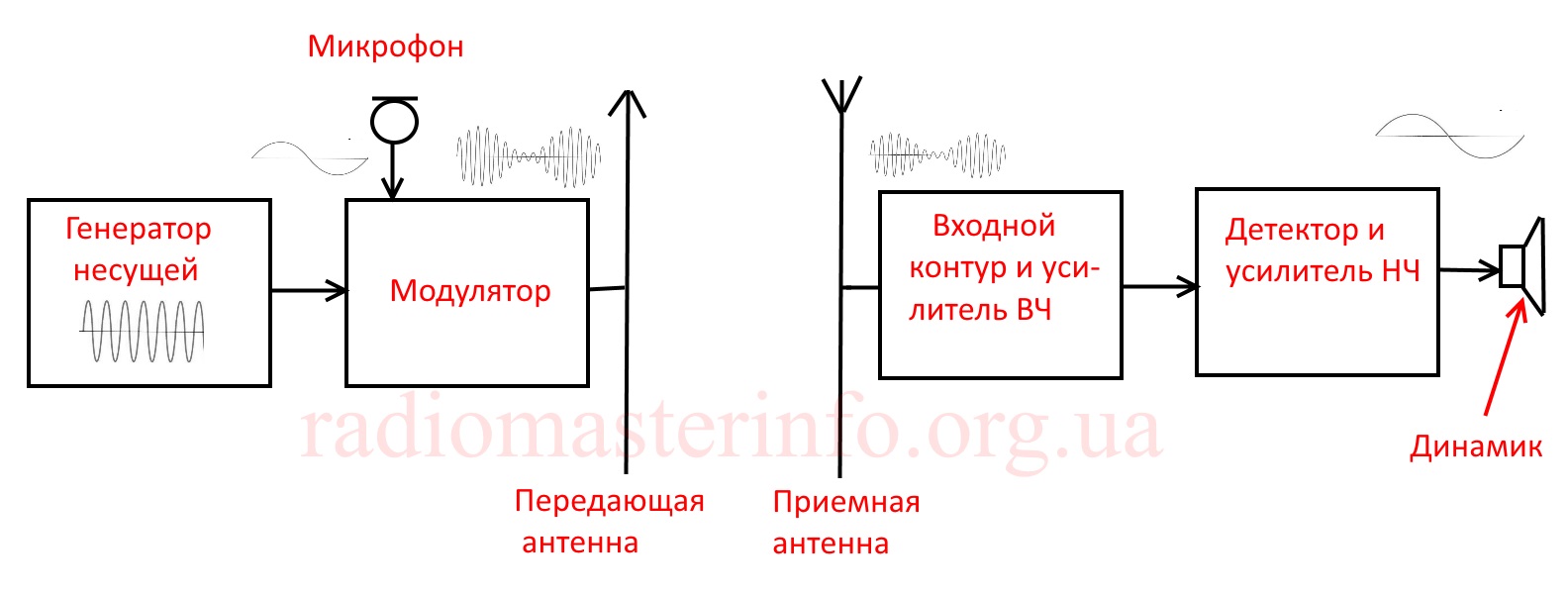
Радиоволны, это высокочастотные колебания электромагнитного поля, способные распространяться в свободном пространстве на значительные расстояния.

Самое привлекательное в этом то, что с помощью радиоволн можно передавать информацию.

Основными параметрами колебаний являются частота, амплитуда, фаза.

Если на передающей стороне изменять один из параметров колебаний, а на приемной стороне выделять это изменение, то таким способом можно передавать информацию на расстояние.

Процесс изменения одного из параметров колебаний в соответствии с передаваемой информацией на передающей стороне называется модуляцией.

Процесс выделения полезной информации из колебаний на приемной стороне, называется детектированием.

Высокочастотные колебания, параметр которых изменяется при передаче называется несущей.

Полезная информация, которая изменяет параметр несущей, называется модулирующим сигналом.

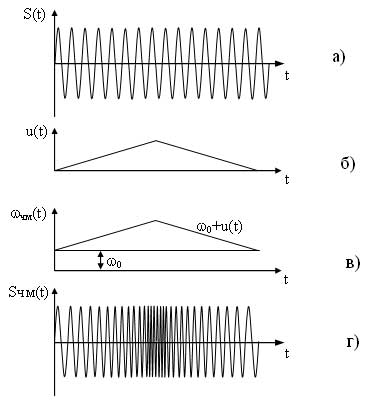
Если, модулирующий сигнал изменяет частоту несущей – то такая модуляция называется частотной. Модуляция частоты однотонным синусоидальным сигналом представлена на рисунке ниже.

Если модулирующий сигнал изменяет амплитуду несущей – то такая модуляция называется амплитудной. Модуляция амплитуды однотонным синусоидальным сигналом представлена на рисунке ниже.

Если модулирующий сигнал изменяет фазу несущей, то такая модуляция называется фазовой.

Простейший вид фазовой модуляции – фазовая манипуляция, когда фаза меняется скачкообразно.

Существует много видов модуляции. Все они имеют преимущества и недостатки.

Вы уже поняли, что частота несущей во много раз превышает частоту модулирующего сигнала. Модулирующий сигнал, например, речь, занимает область частот до 20 кГц, это при высоком качестве звука, в телефонии, где качество звука низкое — до 3 кГц. Сигналы этой частоты самостоятельно не способны распространяться в эфире на большие расстояния, но если мы ними промодулируем высокочастотный сигнал, например, 90 мГц, то сможем передать на большие расстояния.

Примеры наиболее распространенного использования модуляций:

Амплитудная модуляция – радиовещание на длинных, средних и коротких волнах. Передача видеосигнала в наземном телевизионном вещании.

Частотная модуляция – радиовещание на УКВ (и ФМ) диапазонах, передача звука в наземном телевизионном вещании, передача цветоразностных сигналов в наземном телевизионном вещании системы цветности СЕКАМ (была основной в СССР) и т.д.

Фазовая модуляция — передача цветоразностных сигналов в наземном телевизионном вещании системы цветности ПАЛ (основная в Европе).

При передаче информации с помощью радиосигналов основными задачами, с которыми приходится сталкиваться являются:

Чем выше частоты, тем больше каналов связи можно организовать. Но с ростом частот растет сложность и стоимость оборудования. Сейчас мы видим все более интенсивное освоение частот в диапазоне гигагерц (ГГц) и выше.

Структурная схема простого канала передачи звука на расстояние приведена ниже:

С развитием технического прогресса удается более рационально использовать частоты эфира, в котором так тесно. Хорошим тому примером является внедрение цифрового эфирного телевидения стандарта DVB T2. Если раньше, при простом аналоговом способе телевизионного вещания, на одной частоте дециметрового диапазона, например 430 МГц, располагался один телевизионный канал, то в стандарте DVB T2, на этой одной частоте можно расположить пакет из 8 телевизионных каналов с цифровым качеством. Это преимущество настолько явное, что уже идет повсеместное внедрение стандарта DVB T2 и отключение аналогового телевизионного вещания.

Источник

Множество типов радиочастотной модуляции

Радиосвязь построена на простой концепции: постоянно изменяя характеристики синусоиды, мы можем использовать ее для передачи информации.

На этом этапе мы рассмотрели множество важных концепций, которые служат основой для успешного проектирования и анализа реальных радиочастотных схем и систем. Теперь мы готовы исследовать фундаментальный аспект радиотехники: модуляцию.

Что такое модуляция?

Общий смысл глагола «модулировать» означает «модифицировать, регулировать, изменять», и это определяет суть модуляции даже в специализированном контексте беспроводной связи. Модулировать сигнал – это просто преднамеренно изменять его, но, конечно, эта модификация выполняется строго определенным образом, поскольку целью модуляции является передача данных.

Мы хотим передавать информацию – единицы и нули, если мы имеем дело с цифровыми данными, или последовательность постоянно изменяющихся значений, если мы работаем в аналоге. Но ограничения, налагаемые беспроводной связью, не позволяют нам выражать эту информацию обычным способом; вместо этого мы должны разработать новый «язык», или можно сказать «код», который позволит нам передавать ту же информацию, но в рамках ограничений системы на основе электромагнитного излучения. В частности, нам нужен язык, который совместим с высокочастотными синусоидальными сигналами, поскольку такие сигналы являются единственным практическим средством «переноса» информации в типовой радиочастотной системе.

Эта высокочастотная синусоида, которая используется для передачи информации, называется несущей частотой (или просто несущая). Это название полезно, потому что оно напоминает нам о том, что цель радиочастотной системы заключается не в создании и передаче высокочастотной синусоиды. Скорее, целью является передача (низкочастотной) информации, и несущая – это просто средство, которое мы должны использовать для перемещения этой информации от радиочастотного передатчика к радиочастотному приемнику.

Схемы модуляции

В вербальном общении человеческое тело генерирует звуковые волны и модифицирует или модулирует их так, чтобы создавать большое количество гласных и согласных звуков. Разумное использование этих гласных и согласных приводит к передаче информации от говорящего к слушателю. Система, в соответствии с которой модулируются звуковые волны, называется языком.

В радиочастотной связи ситуация очень похожа. Устройство модулирует электрические волны в соответствии с предопределенной системой, называемой схемой модуляции (или способом модуляции). Так же, как существует много человеческих языков, существует множество способов, которыми можно модулировать несущую.

Сложные схемы модуляции помогают современным радиочастотным системам достичь большого расстояния и улучшить устойчивость к помехам

Возможно, что некоторые человеческие языки особенно эффективны в передаче определенных видов информации; если взять пример из древнего мира, возможно, греческий язык был лучше для философов, а латынь лучше приводила в систему законы. Однако нет никаких сомнений в том, что надежная связь возможна с любым надлежащим образом развитым языком, если только оратор и слушатель знают об этом. То же самое верно для радиочастотных систем. Каждая схема модуляции имеет свои преимущества и недостатки, но все они могут обеспечить отличную беспроводную связь, если выполнено основное требование, то есть приемник должен быть способен понять, что говорит передатчик.

Амплитуда, частота, фаза

Базовая синусоида – вещь простая. Если мы игнорируем смещение по постоянному напряжению, ее можно полностью охарактеризовать только двумя параметрами: амплитудой и частотой. У нас также есть фаза, которая вступает в игру, когда мы рассматриваем начальное состояние синусоиды, или когда изменения в волновом поведении позволяют нам отличать одну часть синусоиды от предыдущей. Фаза также имеет значение при сравнении двух синусоид; этот аспект фазы синусоиды стал очень важным из-за широкого использования в радиочастотных системах квадратурных (или «IQ») сигналов. Мы рассмотрим концепции IQ в этом учебнике позже.

Как обсуждалось выше, модуляция – это модификация, и можем изменить только то, что уже присутствует. У синусоид есть амплитуда, частота и фаза, и поэтому неудивительно, что способы модуляции классифицируются как амплитудная модуляция, частотная модуляция или фазовая модуляция. (На самом деле можно объединять эти категории, комбинируя амплитудную модуляцию с частотной или фазовой модуляцией.) В каждой из этих категорий есть две подкатегории: аналоговая модуляция и цифровая модуляция.

Амплитудная модуляция (АМ, англ. AM)

Аналоговая амплитудная модуляция состоит из умножения непрерывно изменяющейся синусоидальной несущей на смещенную версию непрерывно изменяющегося информационного (низкочастотного) сигнала. Под «смещенной версией» я подразумеваю, что мгновенная амплитуда низкочастотного сигнала всегда выше или равна нулю.

Предположим, что у нас есть несущая 10 МГц и низкочастотный сигнал 1 МГц:

Низкочастотный сигнал Несущая частота

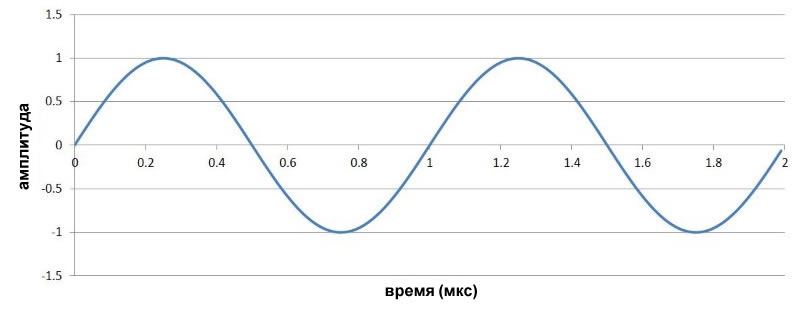
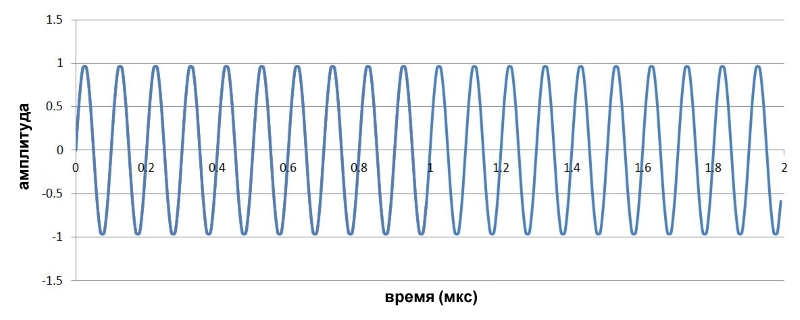
Если мы перемножим эти два сигнала, то получим сигнал следующей (неправильной) формы:

Несущая, умноженная на низкочастотный сигнал

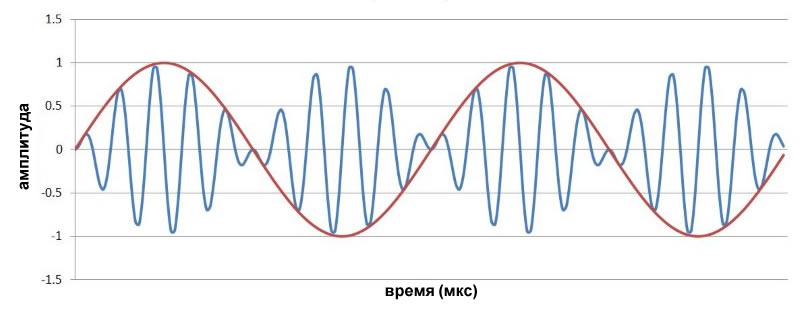
Вы можете четко видеть взаимосвязь между низкочастотным сигналом (красный) и амплитудой несущей (синий).

Но у нас есть проблема: если вы посмотрите только на амплитуду несущей, то как сможете определить, находится ли значение низкочастотного сигнала в положительной или отрицательной полуволне? Это невозможно – и, следовательно, амплитудная демодуляция не будет правильно извлекать низкочастотный сигнал из модулированной несущей.

Смещенный низкочастотный сигнал

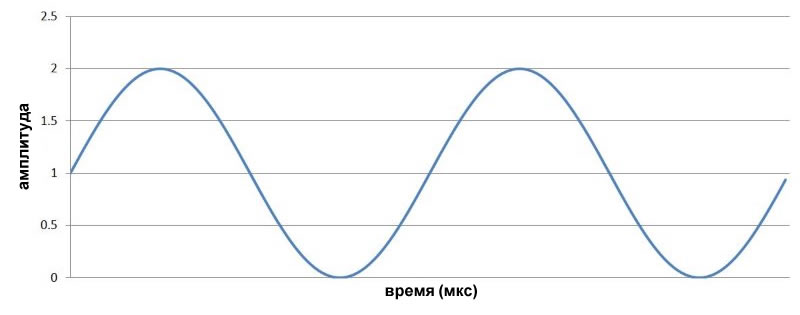
Если мы умножим смещенный низкочастотный сигнал на сигнал несущей, то получим следующее:

Несущая, умноженная на смещенный низкочастотный сигнал

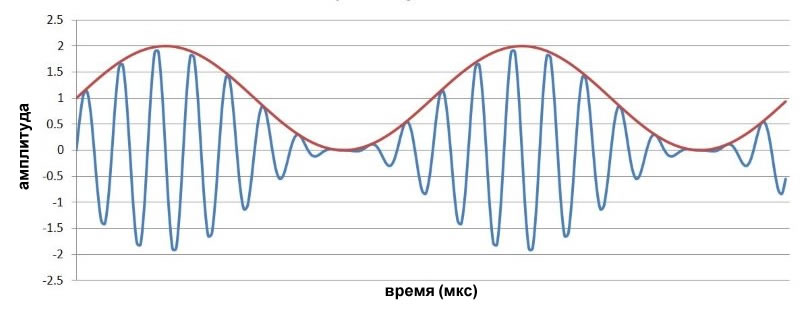
Теперь амплитуда несущей может быть непосредственно соотнесена с поведением низкочастотного сигнала.

Самая простая форма цифровой амплитудной модуляции применяет ту же математическую связь с низкочастотным сигналом, чья амплитуда равна 0 или 1. Результат называется «амплитудная манипуляция» («on-off keying», OOK, или «манипуляция включено-выключено»): когда информационный сигнал равен логическому нулю, амплитуда несущей равна нулю («выключено»); когда информационный сигнал равен логической единице, амплитуда несущей равна максимальному значению («включено»).

Частотная модуляция (ЧМ, англ. FM) и фазовая модуляция (ФМ, англ. PM)

Частотная и фазовая модуляции тесно связаны, потому что частота и фаза тесно связаны между собой. Это не так очевидно, если вы считаете, что частота равна числу полных циклов в секунду – как число циклов в секунду связано с положением синусоиды в заданный момент во времени цикла? Но это имеет смысл, если вы считаете мгновенную частоту, т.е. частоту сигнала в заданный момент (несомненно, парадоксально описывать частоту как мгновенную, но в контексте практической обработки сигналов мы можем смело игнорировать сложные теоретические детали, связанные с этой концепцией).

В базовой синусоиде значение мгновенной частоты совпадает со значением «нормальной» частоты. Аналитическое значение мгновенной частоты появляется, когда мы имеем дело с сигналами, у которых частота изменяется во времени, т.е. частота является не постоянным значением, а скорее функцией времени, записанной как ω(t). В любом случае, важным моментом нашего текущего обсуждения относительно тесной взаимосвязи между частотой и фазой является следующее: мгновенная угловая частота является производной фазы по времени. Поэтому, если у вас есть выражение φ(t), которое описывает изменяющееся во времени поведение фазы сигнала, то скорость изменения φ(t) (по времени), дает вам выражение для мгновенной угловой частоты.

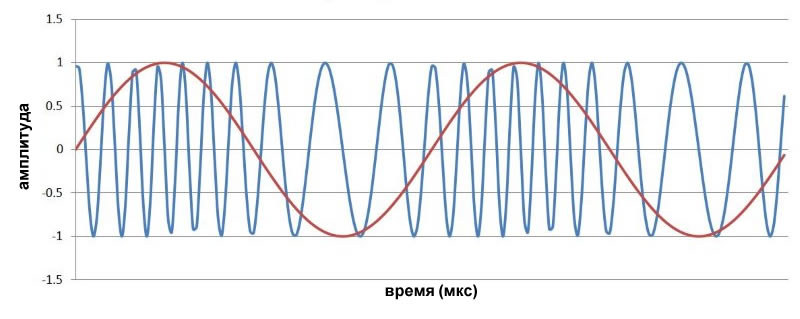
Позже в этой главе мы рассмотрим частотную и фазовую модуляции. А пока давайте закончим следующим графиком, который показывает математическую взаимосвязь в частотной модуляции между низкочастотным сигналом и сигналом несущей частоты, используемых ранее:

Частотная модуляция

Источник

Что такое модуляция и разновидности модулированных сигналов?

Общие сведения о модуляции

Модуляция — это процесс преобразования одного или нескольких информационных параметров несущего сигнала в соответствии с мгновенными значениями информационного сигнала.

В результате модуляции сигналы переносятся в область более высоких частот.

Использование модуляции позволяет:

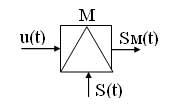
Модуляция осуществляется в устройствах модуляторах. Условное графическое обозначение модулятора имеет вид:

При модуляции на вход модулятора подаются сигналы:

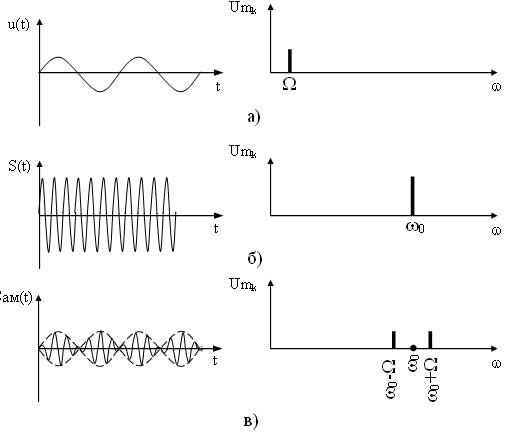
u(t) — модулирующий, данный сигнал является информационным и низкочастотным (его частоту обозначают W или F);

S(t) — модулируемый (несущий), данный сигнал является неинформационным и высокочастотным (его частота обозначается w₀ или f₀);

Sм(t) — модулированный сигнал, данный сигнал является информационным и высокочастотным.

В качестве несущего сигнала может использоваться:

Так как в процессе модуляции изменяются информационные параметры несущего колебания, то название вида модуляции зависит от изменяемого параметра этого колебания.

1. Виды аналоговой модуляции:

2. Виды импульсной модуляции:

Амплитудная модуляция

Амплитудная модуляция — процесс изменения амплитуды несущего сигнала в соответствии с мгновенными значениями модулирующего сигнала.

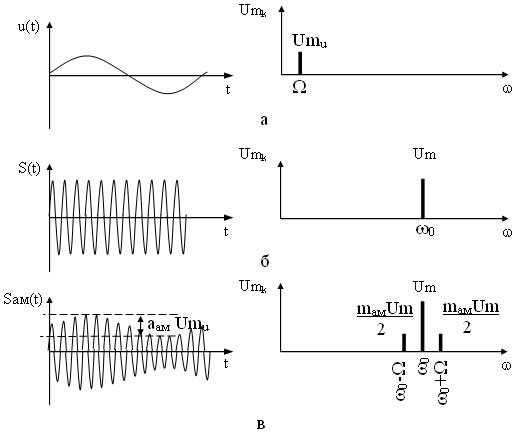
Рассмотрим математическую модель амплитудно-модулированного (АМ) сигнала при гармоническом модулирующем сигнале. При воздействии модулирующего сигнала

на несущее колебание

происходит изменение амплитуды несущего сигнала по закону:

где а_ам — коэффициент пропорциональности амплитудной модуляции.

Подставив (3) в математическую модель (2) получим:

Вынесем Um за скобки:

Отношение а_ам Um_u/Um = m_ам называется коэффициентом амплитудной модуляции. Данный коэффициент не должен превышать единицу, т. к. в этом случае появляются искажения огибающей модулированного сигнала называемые перемодуляцией. С учетом m_ам математическая модель АМ сигнала при гармоническом модулирующем сигнале будет иметь вид:

Если модулирующий сигнал u(t) является негармоническим, то математическая модель АМ сигнала в этом случае будет иметь вид:

Рассмотрим спектр АМ сигнала для гармонического модулирующего сигнала. Для этого раскроем скобки математической модели модулированного сигнала, т. е. представим его в виде суммы гармонических составляющих.

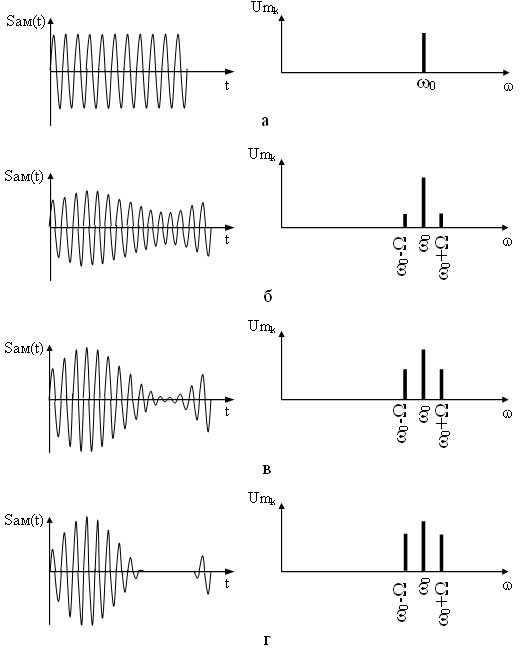
Как видно из выражения в спектре АМ сигнала присутствует три составляющих: составляющая несущего сигнала и две составляющих на комбинационных частотах. Причем составляющая на частоте ?₀—? называется нижней боковой составляющей, а на частоте ?₀ + ? — верхней боковой составляющей. Спектральные и временные диаграммы модулирующего, несущего и амплитудно-модулированного сигналов имеют вид (рисунок 2).

Ширина спектра для данного сигнала будет определятся

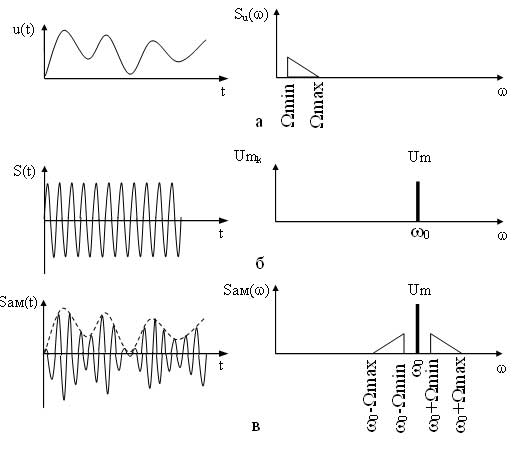
Если же модулирующий сигнал является случайным, то в этом случае в спектре составляющие модулирующего сигнала обозначают символически треугольниками (рисунок 3).

Ширина спектра для данного сигнала будет определятся

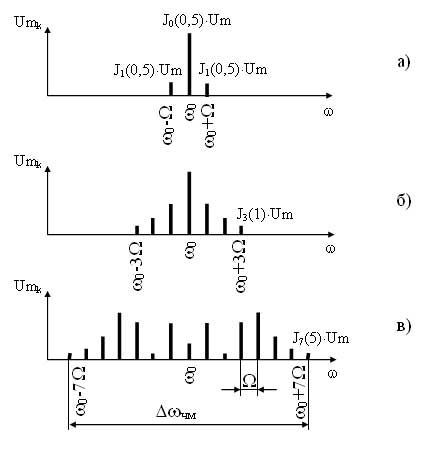
На рисунке 4 приведены временные и спектральные диаграммы АМ сигналов при различных индексах m_ам. Как видно при m_ам=0 модуляция отсутствует, сигнал представляет собой немодулированную несущую, соответственно и спектр этого сигнала имеет только составляющую несущего сигнала (рисунок 4,

а), при индексе модуляции m_ам=1 происходит глубокая модуляция, в спектре АМ сигнала амплитуды боковых составляющих равны половине амплитуды составляющей несущего сигнала (рисунок 4в), данный вариант является оптимальным, т. к. энергия в большей степени приходится на информационные составляющие. На практике добиться коэффициента равного едините тяжело, поэтому добиваются соотношения 0 1 происходит перемодуляция, что, как отмечалось выше, приводит к искажению огибающей АМ сигнала, в спектре такого сигнала амплитуды боковых составляющих превышают половину амплитуды составляющей несущего сигнала (рисунок 4г).

Основными достоинствами амплитудной модуляции являются:

Недостатками этой модуляции являются:

Амплитудная модуляция нашла широкое применение:

Балансная и однополосная модуляция

Как отмечалось выше, одним из недостатков амплитудной модуляции является наличие составляющей несущего сигнала в спектре модулированного сигнала. Для устранения этого недостатка применяют балансную модуляцию. При балансной модуляциипроисходит формирование модулированного сигнала без составляющей несущего сигнала. В основном это осуществляется путем использования специальных модуляторов: балансного или кольцевого. Временная диаграмма и спектр балансно-модулированного (БМ) сигнала представлен на рисунке 5.

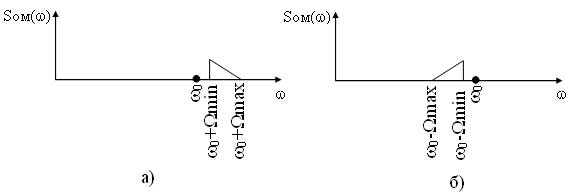
Также особенностью модулированного сигнала является наличие в спектре двух боковых полос несущих одинаковую информацию. Подавление одной из полос позволяет уменьшить спектр модулированного сигнала и, соответственно, увеличить число каналов в линии связи. Модуляция при которой формируется модулированный сигнал с одной боковой полосой (верхней или нижней) называется однополосной. Формирование однополосно-модулированного (ОМ) сигнала осуществляется из БМ сигнала специальными методами, которые рассматриваются ниже. Спектры ОМ сигнала представлены на рисунке 6.

Частотная модуляция

Частотная модуляция — процесс изменения частоты несущего сигнала в соответствии с мгновенными значениями модулирующего сигнала.

Рассмотрим математическую модель частотно-модулированного (ЧМ) сигнала при гармоническом модулирующем сигнале. При воздействии модулирующего сигнала

на несущее колебание

происходит изменение частоты несущего сигнала по закону:

где а_чм — коэффициент пропорциональности частотной модуляции.

Величина Dw_m называется девиацией частоты. Следовательно, девиация частоты показывает наибольшее отклонение частоты модулированного сигнала от частоты несущего сигнала.

называется индексом частотной модуляции.

Учитывая (12) и (13) математическая модель ЧМ сигнала при гармоническом модулирующем сигнале будет иметь вид:

Временные диаграммы, поясняющие процесс формирования частотно-модулированного сигнала приведены на рисунке 7. На первых диаграммах а) и б) представлены соответственно несущий и модулирующий сигналы, на рисунке в) представлена диаграмма показывающая закон изменения частоты ЧМ сигнала. На диаграмме г) представлен частогтно-модулированный сигнал соответствующий заданному модулирующему сигналу, как видно из диаграммы любое изменение амплитуды модулирующего сигнала вызывает пропорциональное изменение частоты несущего сигнала.

Для построения спектра ЧМ сигнала необходимо разложить его математическую модель на гармонические составляющие. В результате разложения получим

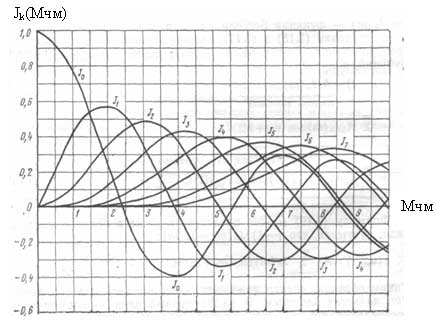
где J_k(Mчм) — коэффициенты пропорциональности.

J_k(Mчм) определяются по функциям Бесселя и зависят от индекса частотной модуляции. На рисунке 8 представлен график содержащий восемь функций Бесселя. Для определения амплитуд составляющих спектра ЧМ сигнала необходимо определить значение функций Бесселя для заданного индекса. Причем как

видно из рисунка различные функции имеют начало в различных значениях Мчм, а следовательно, количество составляющих в спектре будет определятся Мчм (с увеличивается индекса увеличивается и количество составляющих спектра). Например необходимо определить коэффициенты J_k(Мчм) при Мчм=2. По графику видно, что при заданном индексе можно определить коэффициенты для пяти функций (J₀, J₁, J₂, J₃, J₄) Их значение при заданном индексе будет равно: J₀=0,21; J₁=0,58; J₂=0,36; J₃=0,12; J₄=0,02. Все остальные функции начинаются после значения Мчм=2 и равны, соответственно, нулю. Для приведенного примера количество составляющих в спектре ЧМ сигнала будет равно 9: одна составляющая несущего сигнала (Um J₀) и по четыре составляющих в каждой боковой полосе (Um J₁; Um J₂; Um J₃; Um J₄).

Еще одной важной особенностью спектра ЧМ сигнала является то, что можно добиться отсутствия составляющей несущего сигнала или сделать ее амплитуду значительно меньше амплитуд информационных составляющих без дополнительных технических усложнений модулятора. Для этого необходимо подобрать такой индекс модуляции Мчм, при котором J₀(Мчм) будет равно нулю (в месте пересечения функции J₀ с осью Мчм), например Мчм=2,4.

Достоинством частотной модуляции являются:

Основным недостатком данной модуляции является большая ширина спектра модулированного сигнала.

Частотная модуляция используется:

Фазовая модуляция

Фазовая модуляция — процесс изменения фазы несущего сигнала в соответствии с мгновенными значениями модулирующего сигнала.

Рассмотрим математическую модель фазо-модулированного (ФМ) сигнала при гармоническом модулирующем сигнале. При воздействии модулирующего сигнала

на несущее колебание

происходит изменение мгновенной фазы несущего сигнала по закону:

где а_фм — коэффициент пропорциональности частотной модуляции.

Подставляя ?фм(t) в S(t) получаем математическую модель ФМ сигнала при гармоническом модулирующем сигнале:

Произведение а_фм Um_u=Dj_m называется индексом фазовой модуляции или девиацией фазы.

Поскольку изменение фазы вызывает изменение частоты, то используя (11) определяем закон изменения частоты ФМ сигнала:

Произведение а_фмUm_u?=??_m является девиацией частоты фазовой модуляции. Сравнивая девиацию частоты при частотной и фазовой модуляциях можно сделать вывод, что и при ЧМ и при ФМ девиация частоты зависит от коэффициента пропорциональности и амплитуды модулирующего сигнала, но при ФМ девиация частоты также зависит и от частоты модулирующего сигнала.

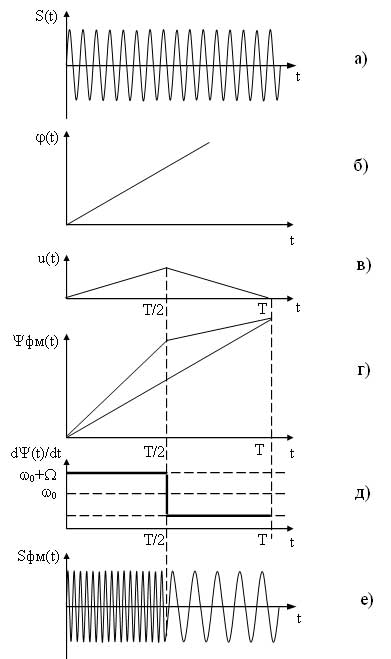
Временные диаграммы поясняющие процесс формирования ФМ сигнала приведены на рисунке 10.

Ширина спектра ФМ сигнала определяется выражением:

Достоинствами фазовой модуляции являются:

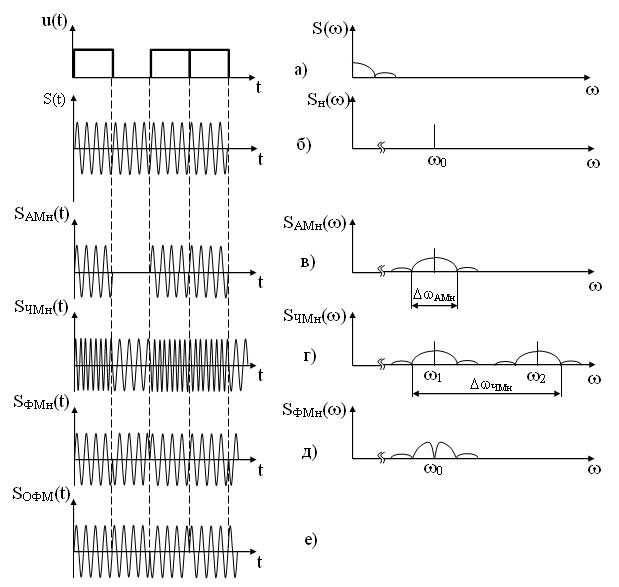
Дискретная двоичная модуляция (манипуляция гармонической несущей)

Дискретная двоичная модуляция (манипуляция) — частный случай аналоговой модуляции, при которой в качестве несущего сигнала используется гармоническая несущая, а в качестве модулирующего сигнала используется дискретный, двоичный сигнал.

Различают четыре вида манипуляции:

Временные и спектральные диаграммы модулированных сигналов при различных видах манипуляции представлены на рисунке 11.

При амплитудной манипуляции, также как и при любом другом модулирующем сигнале огибающая S_АМн(t) повторяет форму модулирующего сигнала (рисунок 11, в).

При фазовой манипуляции фаза несущего сигнала изменяется на 180° в момент изменения амплитуды модулирующего сигнала. Если следует серия из нескольких импульсов, то фаза несущего сигнала на этом интервале не изменяется (рисунок 11, д).

При относительно-фазовой манипуляции фаза несущего сигнала изменяется на 180° лишь в момент подачи импульса, т. е. при переходе от активной паузы к посылке (0?1) или от посылке к посылке (1?1). При уменьшении амплитуды модулирующего сигнала фаза несущего сигнала не изменяется (рисунок 11, е). Спектры сигналов при ФМн и ОФМн имеют одинаковый вид (рисунок 9, е).

Сравнивая спектры всех модулированных сигналов можно отметить, что наибольшую ширину имеет спектр ЧМн сигнала, наименьшую — АМн, ФМн, ОФМн, но в спектрах ФМн и ОФМн сигналов отсутствует составляющая несущего сигнала.

В виду большей помехоустойчивости наибольшее распространение получили частотная, фазовая и относительно-фазовая манипуляции. Различные их виды используются в телеграфии, при передаче данных, в системах подвижной радиосвязи (телефонной, транкинговой, пейджинговой).

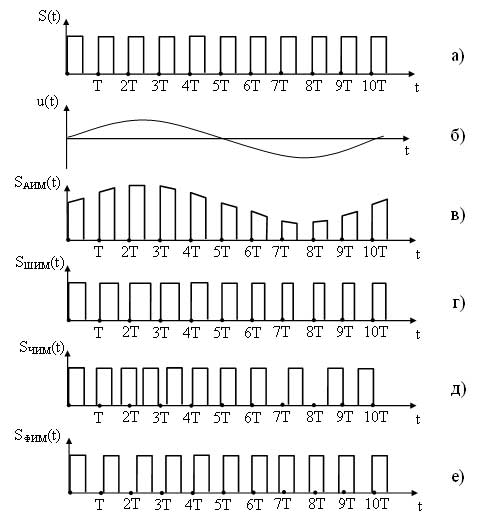
Импульсная модуляция

Импульсная модуляция — это модуляция, при которой в качестве несущего сигнала используется периодическая последовательность импульсов, а в качестве модулирующего может использоваться аналоговый или дискретный сигнал.

Поскольку периодическая последовательность характеризуется четырьмя информационными параметрами (амплитудой, частотой, фазой и длительностью импульса), то различают четыре основных вида импульсной модуляции:

Временные диаграммы импульсно-модулированных сигналов представлены на рисунке 12.

При АИМ происходит изменение амплитуды несущего сигнала S(t) в соответствии с мгновенными значениями модулирующего сигнала u(t), т. е. огибающая импульсов повторяет форму модулирующего сигнала (рисунок 12, в).

При ШИМ происходит изменение длительности импульсов S(t) в соответствии с мгновенными значениями u(t) (рисунок 12, г).

При ЧИМ происходит изменение периода, а соответственно и частоты, несущего сигнала S(t) в соответствии с мгновенными значениями u(t) (рисунок 12, д).

При ФИМ происходит смещение импульсов несущего сигнала относительно их тактового (временного) положения в немодулированной несущей (тактовые моменты обозначены на диаграммах точками Т, 2Т, 3Т и т. д.). ФИМ сигнал представлен на рисунке 12, е.

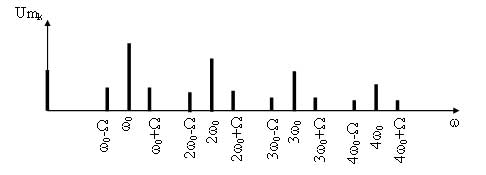
Поскольку при импульсной модуляции переносчиком сообщения является периодическая последовательность импульсов, то спектр импульсно-модулированных сигналов является дискретным и содержит множество спектральных составляющих. Этот спектр представляет собой спектр периодической последовательности импульсов в котором возле каждой гармонической составляющей несущего сигнала находятся составляющие модулирующего сигнала (рисунок 13). Структура боковых полос возле каждой составляющей несущего сигнала зависит от вида модуляции.

Также важной особенностью спектра импульсно-модулированных сигналов является то, что ширина спектра модулированного сигнала, кроме ШИМ, не зависит от модулирующего сигнала. Она полностью определяется длительностью импульса несущего сигнала. Поскольку при ШИМ длительность импульса изменяется и зависит от модулирующего сигнала, то при этом виде модуляции и ширина спектра также зависти от модулирующего сигнала.

Частоту следования импульсов несущего сигнала может быть определена по теореме В. А. Котельникова как f₀ =2Fmax. При этом Fmax это верхняя частота спектра модулирующего сигнала.

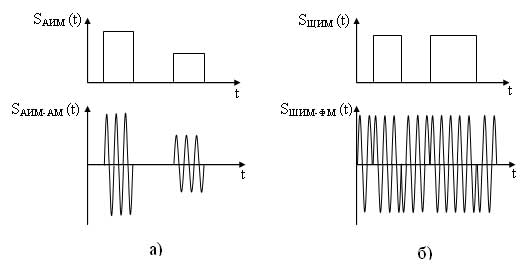
Передача импульсно модулированных сигналов по высокочастотным линиям связи невозможна, т. к. спектр этих сигналов содержит низкочастотные составляющий. Поэтому для передачи осуществляют повторную модуляцию. Это модуляция, при которой в качестве модулирующего сигнала используют импульсно-модулированный сигнал, а в качестве несущего гармоническое колебание. При повторной модуляции спектр импульсно-модулированного сигнала переносится в область несущей частоты. Для повторной модуляции может использоваться любой из видов аналоговой модуляции: АМ, ЧС, ФМ. Полученная модуляция обозначается двумя аббревиатурами: первая указывает на вид импульсной модуляции а вторая — на вид аналоговой модуляции, например АИМ-АМ (рисунок 14, а) или ШИМ-ФМ (рисунок 14, б) и т. д.

Источник