Что такое модель каковы основные свойства моделей

Модель

Построение и исследование моделей, то есть моделирование, облегчает изучение имеющихся в реальном устройстве (процессе, …) свойств и закономерностей. Применяют для нужд познания (созерцания, анализа и синтеза).

Моделирование является обязательной частью исследований и разработок, неотъемлемой частью нашей жизни, поскольку сложность любого материального объекта и окружающего его мира бесконечна вследствие неисчерпаемости материи и форм её взаимодействия внутри себя и с внешней средой.

Одни и те же устройства, процессы, явления и т. д. (далее — «системы») могут иметь много разных видов моделей. Как следствие, существует много названий моделей, большинство из которых отражает решение некоторой конкретной задачи. Ниже приведена классификация и дана характеристика наиболее общих видов моделей.

Содержание

Требования к моделям

Моделирование всегда предполагает принятие допущений той или иной степени важности. При этом должны удовлетворяться следующие требования к моделям:

Выбор модели и обеспечение точности моделирования считается одной из самых важных задач моделирования.

Точность моделей

Погрешности моделирования вызываются как объективными причинами, связанными с упрощением реальных систем, так и субъективными, обусловленными недостатком знаний и навыков, особенностями характера того или иного человека. Погрешности можно предотвратить, компенсировать или учесть. И всегда обязательна оценка правильности получаемых результатов. В технике быструю оценку точности модели часто проводят следующими способами:

Известно, что посредством грубых измерений, использования контрольно-измерительных приборов с низкой точностью или приближенных исходных данных невозможно получить точные результаты. С другой стороны, бессмысленно вести, например, расчет с точностью до грамма, если результат потом нужно округлять (скажем, указывать в формуляре) с точностью до ста грамм, или же определять среднюю величину точнее составляющих её значений, и т. д. Поэтому важно помнить о следующем:

Основные виды моделей

По способу отображения действительности различают три основных вида моделей — эвристические, натурные и математические.

Эвристические модели

Эвристические модели, как правило, представляют собой образы, рисуемые в воображении человека. Их описание ведется словами естественного языка (например, вербальная информационная модель) и, обычно, неоднозначно и субъективно. Эти модели неформализуемы, то есть не описываются формально-логическими и математическими выражениями, хотя и рождаются на основе представления реальных процессов и явлений.

Эвристическое моделирование — основное средство вырваться за рамки обыденного и устоявшегося. Но способность к такому моделированию зависит, прежде всего, от богатства фантазии человека, его опыта и эрудиции. Эвристические модели используют на начальных этапах проектирования или других видов деятельности, когда сведения о разрабатываемой системе ещё скудны. На последующих этапах проектирования эти модели заменяют на более конкретные и точные.

Натурные модели

Отличительной чертой этих моделей является их подобие реальным системам (они материальны), а отличие состоит в размерах, числе и материале элементов и т. п. По принадлежности к предметной области модели подразделяют на следующие:

Физическое моделирование — основа наших знаний и средство проверки наших гипотез и результатов расчетов. Физическая модель позволяет охватить явление или процесс во всём их многообразии, наиболее адекватна и точна, но достаточно дорога, трудоемка и менее универсальна. В том или ином виде с физическими моделями работают на всех этапах проектирования;

Математические модели

Математические модели — формализуемые, то есть представляют собой совокупность взаимосвязанных математических и формально-логических выражений, как правило, отображающих реальные процессы и явления (физические, психические, социальные и т. д.). По форме представления бывают:

Построение математических моделей возможно следующими способами (более подробно — см. Математическая модель):

Математические модели более универсальны и дешевы, позволяют поставить «чистый» эксперимент (то есть в пределах точности модели исследовать влияние какого-то отдельного параметра при постоянстве других), прогнозировать развитие явления или процесса, отыскать способы управления ими. Математические модели — основа построения компьютерных моделей и применения вычислительной техники.

Результаты математического моделирования нуждаются в обязательном сопоставлении с данными физического моделирования — с целью проверки получаемых данных и для уточнения самой модели. С другой стороны, любая формула — это разновидность модели и, следовательно, не является абсолютной истиной, а всего лишь этап на пути её познания.

Промежуточные виды моделей

К промежуточным видам моделей можно отнести:

Существует и другие виды «пограничных» моделей, например, экономико-математическая и т. д.

Выбор типа модели зависит от объема и характера исходной информации о рассматриваемом устройстве и возможностей инженера, исследователя. По возрастанию степени соответствия реальности модели можно расположить в следующий ряд: эвристические (образные) — математические — натурные (экспериментальные).

Уровни моделей

Количество параметров, характеризующих поведение не только реальной системы, но и её модели, очень велико. Для упрощения процесса изучения реальных систем выделяют четыре уровня их моделей, различающиеся количеством и степенью важности учитываемых свойств и параметров. Это — функциональная, принципиальная, структурная и параметрическая модели.

Функциональная модель

Функциональная модель предназначена для изучения особенностей работы (функционирования) системы и её назначения во взаимосвязи с внутренними и внешними элементами.

Функция — самая существенная характеристика любой системы, отражает её предназначение, то, ради чего она была создана. Подобные модели оперируют, прежде всего, с функциональными параметрами. Графическим представлением этих моделей служат блок-схемы. Они отображают порядок действий, направленных на достижение заданных целей (т. н. ‘функциональная схема’). Функциональной моделью является абстрактная модель.

Модель принципа действия

Модель принципа действия (принципиальная модель, концептуальная модель) характеризует самые существенные (принципиальные) связи и свойства реальной системы. Это — основополагающие физические, биологические, химические, социальные и т. п. явления, обеспечивающие функционирование системы, или любые другие принципиальные положения, на которых базируется планируемая деятельность или исследуемый процесс. Стремятся к тому, чтобы количество учитываемых свойств и характеризующих их параметров было небольшим (оставляют наиболее важные), а обозримость модели — максимальной, так чтобы трудоемкость работы с моделью не отвлекала внимание от сущности исследуемых явлений. Как правило, описывающие подобные модели параметры — функциональные, а также физические характеристики процессов и явлений. Принципиальные исходные положения (методы, способы, направления и т. д.) лежат в основе любой деятельности или работы.

Так, принцип действия технической системы — это последовательность выполнения определенных действий, базирующихся на определенных физических явлениях (эффектах), которые обеспечивают требуемое функционирование этой системы. Примеры моделей принципа действия: фундаментальные и прикладные науки (например, принцип построения модели, исходные принципы решения задачи), общественная жизнь (например, принципы отбора кандидатов, оказания помощи), экономика (например, принципы налогообложения, исчисления прибыли), культура (например, художественные принципы).

Работа с моделями принципа действия позволяет определить перспективные направления разработки (например, механика или электротехника) и требования к возможным материалам (твердые или жидкие, металлические или неметаллические, магнитные или немагнитные и т. д.).

Правильный выбор принципиальных основ функционирования предопределяет жизнеспособность и эффективность разрабатываемого решения. Так, сколько бы ни совершенствовали конструкцию самолета с винтомоторным двигателем, он никогда не разовьет сверхзвуковую скорость, не говоря уже о полетах на больших высотах. Только использование другого физического принципа, например, реактивного движения и созданного на его основе реактивного двигателя, позволит преодолеть звуковой барьер.

Например, для технических моделей эти схемы отражают процесс преобразования вещества, как материальной основы устройства, посредством определенных энергетических воздействий с целью реализации потребных функций (функционально-физическая схема). На схеме виды и направления воздействия, например, изображаются стрелками, а объекты воздействия — прямоугольниками.

Структурная модель

Четкого определения структурной модели не существует. Так, под структурной моделью устройства могут подразумевать:

Под структурной моделью процесса обычно подразумевают характеризующую его последовательность и состав стадий и этапов работы, совокупность процедур и привлекаемых технических средств, взаимодействие участников процесса.

Например, — это могут быть упрощенное изображение звеньев механизма в виде стержней, плоских фигур (механика), прямоугольники с линиями со стрелками (теория автоматического управления, блок-схемы алгоритмов), план литературного произведения или законопроекта и т. д. Степень упрощения зависит от полноты исходных данных об исследуемом устройстве и потребной точности результатов. На практике виды структурных схем могут варьироваться от несложных небольших схем (минимальное число частей, простота форм их поверхностей) до близких к чертежу изображений (высокая степень подробности описания, сложность используемых форм поверхностей).

Возможно изображение структурной схемы в масштабе. Такую модель относят к структурно-параметрической. Её примером служит кинематическая схема механизма, на которой размеры упрощенно изображенных звеньев (длины линий-стержней, радиусы колес-окружностей и т. д.) нанесены в масштабе, что позволяет дать численную оценку некоторым исследуемым характеристикам.

Для повышения полноты восприятия на структурных схемах в символьном (буквенном, условными знаками) виде могут указывать параметры, характеризующие свойства отображаемых систем. Исследование таких схем позволяет установить соотношения (функциональные, геометрические и т. п.) между этими параметрами, то есть представить их взаимосвязь в виде равенств f (x₁, х₂, …) = 0, неравенств f (x₁, х₂, …) > 0 и в иных выражениях.

Параметрическая модель

Под параметрической моделью понимается математическая модель, позволяющая установить количественную связь между функциональными и вспомогательными параметрами системы. Графической интерпретацией такой модели в технике служит чертеж устройства или его частей с указанием численных значений параметров.

Классификация моделей

По целям исследований

В зависимости от целей исследования выделяют следующие модели:

По особенностям представления

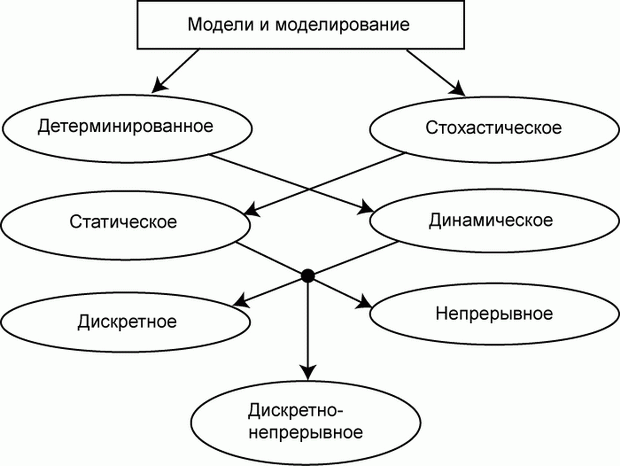
С целью подчеркнуть отличительную особенность модели их подразделяют на простые и сложные, однородные и неоднородные, открытые и закрытые, статические и динамические, вероятностные и детерминированные и т. д. Стоит отметить, что когда говорят, например, о техническом устройстве как простом или сложном, закрытом или открытом и т. п., в действительности подразумевают не само устройство, а возможный вид его модели, таким образом подчеркивая особенность состава или условий работы.

Знание этих особенностей облегчает процесс моделирования, так как позволяет выбрать вид модели, наилучшим образом соответствующей заданным условиям. Этот выбор основывается на выделении в системе существенных и отбрасывании второстепенных факторов и должен подтверждаться исследованиями или предшествующим опытом. Наиболее часто в процессе моделирования ориентируются на создание простой модели, что позволяет сэкономить время и средства на её разработку. Однако повышение точности модели, как правило, связано с ростом её сложности, так как необходимо учитывать большое число факторов и связей. Разумное сочетание простоты и потребной точности и указывает на предпочтительный вид модели.

Источник

Информатика Очень надо помогите ответить на вопросы

Задание 1
Что такое модель? Каковы основные свойства моделей?
Решение
Модель — это объект, который используется в качестве «заместителя», представителя другого объекта (оригинала) с определённой целью. Модель не является точной копией объекта-оригинала: она отражает только часть его свойств, отношений и особенностей поведения. Можно создавать и использовать разные модели одного и того же объекта.

Задание 2
Что такое моделирование?
Решение
Процесс создания и использования модели называют моделированием.

Задание 3
Как можно назвать отношение между объектом-оригиналом и его моделью?
Решение
Отношение между объектом-оригиналом и его моделью называют масштабом (уменьшенная копия).

Задание 4
Какие модели называют натурными? Приведите 2-3 примера натурных моделей.
Решение
Натурные модели — реальные предметы, в уменьшенном или увеличенном виде воспроизводящие внешний вид, структуру или поведение объекта моделирования.
Например: глобус, модель корабля.

Задание 6
Для каждой из перечисленных моделей назовите действия, которые человек может выполнить и с ней, и с объектом-оригиналом:
а) радиоуправляемая модель самолёта;
б) словесное описание куртки;
в) план квартиры;
г) чайник из пластилина в натуральную величину;
д) мысленное представление о будущей поездке.
Какие действия могут быть выполнены только с оригиналом?
Решение
а) С моделью: управлять через пульт управления.
С оригиналом: управлять, сидя в кабине пилота.
б) С моделью: обсуждать.
С оригиналом: одеть.
в) С моделью: изменять что-то в плане, чертить.
С оригиналом: жить в квартире.
г) С моделью: любоваться им, изменить форму.
С оригиналом: кипятить в нём воду.
д) С моделью: думать о ней, изменить представление.
С оригиналом: быть уже в пути и ждать её завершения.
Только с оригиналом можно ощутить размер, потрогать.

Задание 7
В какой ситуации искусственные цветы и муляжи фруктов могут использоваться в качестве моделей-«заместителей» настоящих цветов и фруктов? Какие свойства и отношения объектов отражают эти модели, а какие — нет?
Решение
Муляжи цветов и фруктов можно использовать в общественных местах, там где муляжи должны долго находиться в суровых условиях.
Задание 8
Назовите объекты, модели которых приведены на рис. 28-30.
Назовите образные и знаковые элементы каждой модели. Для каждой модели поясните, смысл каких знаков нужно знать, чтобы получить информацию с помощью этой модели.
Решение
На рисунке 28 представлена модель музыкального произведения, она записывается с помощью нот.
На рисунке 29 представлена модель зависимости пути от времени, записывается с помощью графика и формулы.
На рисунке 30 представлена модель местности, записывается с помощью плана.

Источник

Понятие модели и моделирования

1.2.3. Классификация моделей и моделирования по признаку «способ реализации модели»

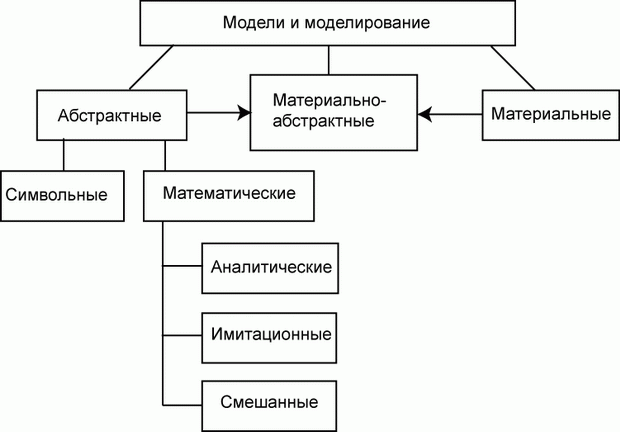
Согласно этому признаку модели делятся на два обширных класса:

Нередко в практике моделирования присутствуют смешанные, абстрактно-материальные модели.

Абстрактные модели представляют собой определенные конструкции из общепринятых знаков на бумаге или другом материальном носителе или в виде компьютерной программы.

Абстрактные модели, не вдаваясь в излишнюю детализацию, можно разделить на:

Символическая модель может иметь самостоятельное значение, но, как правило, ее построение является начальным этапом любого другого моделирования.

Математические модели могут быть:

Преобразование математических моделей по известным законам и правилам можно рассматривать как эксперименты. Решение на основе аналитических моделей может быть получено в результате однократного просчета безотносительно к конкретным значениям характеристик («в общем виде»). Это наглядно и удобно для выявления закономерностей. Однако для сложных систем построить аналитическую модель, достаточно полно отражающую реальный процесс, удается не всегда. Тем не менее, есть процессы, например, марковские, актуальность моделирования которых аналитическими моделями доказана практикой.

В чем заключается отличие имитационных и аналитических моделей?

В случае аналитического моделирования ЭВМ является мощным калькулятором, арифмометром. Аналитическая модель решается на ЭВМ.

Имитационные модели достаточно просто учитывают влияние случайных факторов. Для аналитических моделей это серьезная проблема. При наличии случайных факторов необходимые характеристики моделируемых процессов получаются многократными прогонами (реализациями) имитационной модели и дальнейшей статистической обработкой накопленной информации. Поэтому часто имитационное моделирование процессов со случайными факторами называют статистическим моделированием.

Если исследование объекта затруднено использованием только аналитического или имитационного моделирования, то применяют смешанное (комбинированное), аналитико-имитационное моделирование. При построении таких моделей процессы функционирования объекта декомпозируются на составляющие подпроцессы, и для которых, возможно, используют аналитические модели, а для остальных подпроцессов строят имитационные модели.

1.3. Этапы моделирования

Первый этап: уяснение целей моделирования. Вообще-то это главный этап любой деятельности. Цель существенным образом определяет содержание остальных этапов моделирования. Заметим, что различие между простой системой и сложной порождается не столько их сущностью, но и целями, которые ставит исследователь.

Обычно целями моделирования являются:

Третий этап: выбор языка программирования или моделирования, разработка алгоритма и программы модели. Модель может быть аналитической или имитационной, или их сочетанием. В случае аналитической модели исследователь должен владеть методами решения.

В истории математики (а это, впрочем, и есть история математического моделирования) есть много примеров тому, когда необходимость моделирования разного рода процессов приводила к новым открытиям. Например, необходимость моделирования движения привела к открытию и разработке дифференциального исчисления (Лейбниц и Ньютон) и соответствующих методов решения. Проблемы аналитического моделирования остойчивости кораблей привели академика Крылова А. Н. к созданию теории приближенных вычислений и аналоговой вычислительной машины.

Четвертый этап: планирование эксперимента. Математическая модель является объектом эксперимента. Эксперимент должен быть в максимально возможной степени информативным, удовлетворять ограничениям, обеспечивать получение данных с необходимой точностью и достоверностью. Существует теория планирования эксперимента, нужные нам элементы этой теории мы изучим в соответствующем месте дисциплины.

Пятый этап: выполнение эксперимента с моделью. Если модель аналитическая, то эксперимент сводится к выполнению расчетов при варьируемых исходных данных. При имитационном моделировании модель реализуется на ЭВМ с фиксацией и последующей обработкой получаемых данных. Эксперименты проводятся в соответствии с планом, который может быть включен в алгоритм модели. В современных системах моделирования такая возможность есть.

На этом рассмотрение последовательности моделирования закончим, сделав весьма важный вывод о необходимости документирования результатов каждого этапа. Это необходимо в силу следующих причин.

Во-первых, моделирование процесс итеративный, то есть с каждого этапа может осуществляться возврат на любой из предыдущих этапов для уточнения информации, необходимой на этом этапе, а документация может сохранить результаты, полученные на предыдущей итерации.

Во-вторых, в случае исследования сложной системы в нем участвуют большие коллективы разработчиков, причем различные этапы выполняются различными коллективами. Поэтому результаты, полученные на каждом этапе, должны быть переносимы на последующие этапы, то есть иметь унифицированную форму представления и понятное другим заинтересованным специалистам содержание.

Источник

Что такое модель каковы основные свойства моделей

3. Понятия содержательной модели, математической модели. Постулаты. Параметры и характеристики моделей. Свойства моделей.

Понятие модели

Множество окружающих нас предметов и явлений обладают различными свойствами. Процесс познания этих свойств состоит в том, что мы создаем для себя некоторое представление об изучаемом объекте, помогающее лучше понять его внутреннее состояние, законы функционирования, основные характеристики. Такое представление, выраженное в той либо иной форме, называется моделью. Как отмечается в [3], под моделью следует понимать любую другую систему, обладающую той же формальной структурой, при условии, что между системными характеристиками модели и оригиналом существует соответствие, и она более проста и доступна для изучения и исследования основных свойств объекта-оригинала.

Любая модель есть объект-заменитель объекта-оригинала, обеспечивающий изучение некоторых свойств оригинала.

С точки зрения философии моделирование следует рассматривать как эффективное средство познания природы. При этом процесс моделирования предполагает наличие объекта исследования, исследователя-экспериментатора и модели.

В автоматизированных системах обработки информации и управления в качестве объекта моделирования могут выступать производственно-технологические процессы получения конечных продуктов; процессы движения документов, информационных потоков при реализации учрежденческой деятельности организации; процессы функционирования комплекса технических средств; процессы организации и функционирования информационного обеспечения АСУ; процессы функционирования программного обеспечения АСУ [2].

Преимущества моделирования состоят в том, что появляется возможность сравнительно простыми средствами изучать свойства системы, изменять ее параметры, вводить целевые и ресурсные характеристики внешней среды.

Как правило, моделирование используется на следующих этапах [2]:

· исследования системы до того, как она спроектирована, с целью определения ее основных характеристик и правил взаимодействия элементов между собой и с внешней средой;

· проектирования системы для анализа и синтеза различных видов структур и выбора наилучшего варианта реализации с учетом сформулированных критериев оптимальности и ограничений;

· эксплуатации системы для получения оптимальных режимов функционирования и прогнозируемых оценок ее развития.

При этом одну и ту же систему можно описать различными типами моделей. Например, транспортную сеть некоторого района можно промоделировать электрической схемой, гидравлической системой, математической моделью с использованием аппарата теории графов.

Для исследования систем широко используются следующие типы моделей: физические (геометрического подобия, электрические, механические и др.) и символические (содержательные и математические).

1. Когнетивная модель.

При наблюдении за объектом в голове у исследователя формируется некий мыслительный образ объекта, его идеализированная модель (Мыслительная модель, способствующая к познанию).

При формировании когнитивной модели исследователи стремятся найти ответы на конкретные вопросы, поэтому от сложного устройства или объекта отсекается все второстепенное с целью оконечного описания.

2. Содержательная модель.

Представление когнетивной модели на естественном языке называется содержательной моделью. Содержательная модель не равна когнетивной, так как не всегда исследователь может выразить в знаковой форме все элементы мысленного образа объекта.

В естественнонаучной дисциплине и в технике содержательную модель называют технической постановкой проблемы.

По функциональному признаку и цели содержательные модели подразделяют на описательные, объяснительные и прогнозирующие.

· Описательные – любое описание объекта.

· Объяснительные – отвечают на вопрос: почему что-либо происходит?

· Прогнозирующие – описывают будущее поведение объекта.

3. Концептуальная модель.

Это содержательная модель, при формулировке которой используется понятие и представление предметных областей знаний занимающихся изучением объекта моделирования.

4. Формальная модель.

Если для описания системы используется естественный язык (язык общения между людьми), то такое описание называется содержательной моделью. Примерами содержательных моделей являются словесные постановки задач, программы и планы развития систем, деревья целей организации и др. Содержательные модели имеют самостоятельную ценность при решении задач исследования и управления системами, а также используются в качестве предварительного шага при разработке математических моделей. Поэтому качество математической модели зависит от качества соответствующей математической модели [9].

В качестве языковых средств описания содержательных моделей используются естественный язык (язык общения между людьми), диаграммы, таблицы, блок-схемы, графы.

Математическая модель

Под математической моделью понимается совокупность математических выражений, описывающих поведение (структуру) системы и те условия (возмущения, ограничения), в которых она работает. В свою очередь, математические модели в зависимости от используемого математического аппарата подразделяются, например:

· на статические и динамические;

· детерминированные и вероятностные;

· дискретные и непрерывные;

· аналитические и численные.

Свойства моделей(из презентации):

n Открытость (модифицируемость)

Свойства модели:

При изучении реально существующей или гипотетической системы математические методы применяют к ее математической модели. Это применение будет эффективным, если свойства ММ удовлетворяют определенным требованиям. Рассмотрим эти свойства.

Полнота ММ позволяет отразить в достаточной мере именно те характеристики и особенности системы, которые интересуют нас с точки зрения поставленной цели проведения вычислительного эксперимента. Например,

модель может достаточно полно описывать протекающие в системе процессы, но не отражать его габаритные, массовые или стоимостные показатели.

Точность ММ дает возможность обеспечить приемлемое совпадение реальных и найденных при помощи ММ значений выходных параметров системы

Адекватность ММ — это способность ММ отражать свойства системы с относительной погрешностью не хуже заданной.

В общем смысле под адекватностью ММ понимают правильное качественное и достаточно точное количественное описание именно тех характеристик системы, которые важны в данном конкретном случае. Модель, адекватная при выборе одних характеристик, может быть неадекватной при выборе других характеристик системы. В ряде прикладных областей, еще недостаточно подготовленных к применению количественных математических методов, ММ имеют главным образом качественный характер. Эта ситуация типична, например, для биологической и социальной сфер, в которых количественные закономерности не всегда поддаются строгой математической формализации. В таких случаях под адекватностью ММ естественно понимать лишь правильное качественное описание поведения изучаемых систем.

Экономичность ММ оценивают затратами на вычислительные ресурсы (машинное время и память), необходимые для реализации ММ на ЭВМ. Эти затраты зависят от числа арифметических операций при использовании модели, от размерности пространства фазовых переменных, от особенностей применяемой ЭВМ и других факторов. Очевидно, что требования экономичности, высокой точности и достаточно широкой области адекватности ММ противоречивы и на практике могут быть удовлетворены лишь на основе разумного компромисса. Свойство экономичности ММ часто связывают с ее простотой. Более того, количественный анализ некоторых упрощенных вариантов ММ может быть осуществлен и без привлечения современной вычислительной техники. Однако его результаты могут иметь лишь ограниченную ценность на стадии отладки алгоритма или программы, если упрощение ММ не согласовано с концептуальной моделью системы.

Робастность ММ характеризует ее устойчивость по отношению к погрешностям исходных данных, способность нивелировать эти погрешности и не допускать их чрезмерного влияния на результат вычислительного эксперимента. Причинами низкой робастности ММ могут быть необходимость при ее количественном анализе вычитания близких друг к другу приближенных значений величин или деления на малую по модулю величину, а также использование в ММ функций, быстро изменяющихся в промежутке, где значение аргумента известно с невысокой точностью.

Продуктивность ММ связана с достоверностью исходных данных. Если они являются результатом измерений, то точность их измерения должна быть выше, чем для тех параметров, которые получаются при использовании ММ. В противном случае ММ будет непродуктивной и ее применение для анализа конкретной системы потеряет смысл. Ее можно будет использовать лишь для оценки и характеристик некоторого класса систем с гипотетическими исходными данными.

Наглядность ММ является желательным, но необязательным свойством. Однако использование ММ и ее модификация упрощаются, если ее составляющие (например, отдельные члены уравнений) имеют ясный содержательный смысл. Это позволяет предвидеть результаты вычислительного эксперимента и облегчить контроль их правильности.

Вариант 2 (свойства)

1. Конечность: модель отображает оригинал лишь в конечном числе его отношений и, кроме того, ресурсы моделирования конечны;

2. Упрощенность: модель отображает только существенные стороны объекта;

3. Приблизительность: действительность отображается моделью грубо или приблизительно;

4. Адекватность: насколько успешно модель описывает моделируемую систему;

6. Потенциальность: предсказуемость модели и её свойств;

7. Сложность: удобство её использования;

8. Полнота: учтены все необходимые свойства;

Параметризация моделей (вариант 2)

Теоретические исследования сложных систем базируются на использовании моделей, отображающих объект исследования в форме, необходимой и достаточной для получения результатов, составляющих цель исследований.

Количественно любая модель, как и соответствующая ей система, описывается совокупностью величин, которые могут быть разбиты на параметры и характеристики. Состав параметров и характеристик модели определяется составом параметров и характеристик исследуемой системы и может в идеальном случае совпадать с ним. В общем случае составы параметров и характеристик модели и системы различаются, т.к. в первом случае они формулируются в терминах того математического аппарата, который используется при построении модели, а параметры и характеристики системы формулируются в терминах соответствующей прикладной области, к которой принадлежит система. В связи с тем, что, в общем случае, параметры и характеристики системы и модели различаются, их принято называть соответственно системными и модельными.

В связи с тем, что состав и номенклатура системных и модельных параметров и характеристик, в общем случае, различается, возникает необходимость установления соответствия между значениями системных и модельных параметров и характеристик, которое выполняется на этапе параметризации модели.

1.1.6. Параметры и характеристики

Количественно любая система описывается совокупностью величин, которые могут быть разбиты на два класса:

· параметры, описывающие первичные свойства системы и являющиеся исходными данными при решении задач анализа;

· характеристики, описывающие вторичные свойства системы и определяемые в процессе решения задач анализа как функция параметров, то есть эти величины являются вторичными по отношению к параметрам.

Множество параметров технических систем можно разделить на:

· внутренние, описывающие структурно-функциональную организацию системы, к которым относятся:

q структурные параметры, описывающие состав и структуру системы;

q функциональные параметры, описывающие функциональную организацию (режим функционирования) системы.

· внешние, описывающие взаимодействие системы с внешней по отношению к ней средой, к которым относятся:

q нагрузочные параметры, описывающие входное воздействие на систему, например частоту и объем используемых ресурсов системы;

q параметры внешней (окружающей) среды, описывающие обычно неуправляемое воздействие внешней среды на систему, например помехи и т.п.

Параметры могут быть:

· детерминированными или случайными;

· управляемыми или неуправляемыми.

Характеристики системы делятся на:

· глобальные, описывающие эффективность системы в целом;

· локальные, описывающие качество функционирования отдельных элементов или частей (подсистем) системы.

К глобальным характеристикам технических систем относятся:

·мощностные (характеристики производительности), описывающие скоростные качества системы, измеряемые, например, количеством задач, выполняемых вычислительной системой за единицу времени;

· временные (характеристики оперативности), описывающие временные аспекты функционирования системы, например время решения задач в вычислительной системе;

· надежностные (характеристики надежности), описывающие надежность функционирования системы;

· экономические (стоимостные) в виде стоимостных показателей, например, стоимость технических и программных средств вычислительной системы, затраты на эксплуатацию системы и т.п.;

· прочие: масса-габаритные, энергопотребления, тепловые и т.п.

Таким образом, параметры системы можно интерпретировать как некоторые входные величины, а характеристики – выходные величины, зависящие от параметров и определяемые в процессе анализа системы

Тогда закон функционирования системы можно представить в следующем виде:

где fс – функция, функционал, логические условия, алгоритм, таблица или словесное описание, определяющее правило (закон) преобразования входных величин (параметров) в выходные величины (характеристики);

H(t) – вектор характеристик, зависящий от текущего момента времени t

Источник