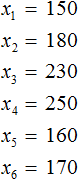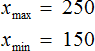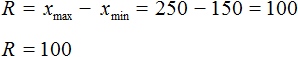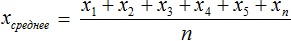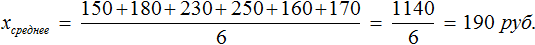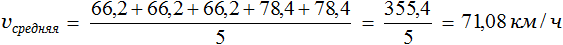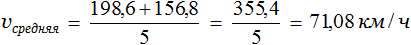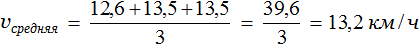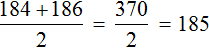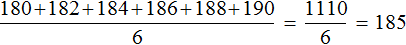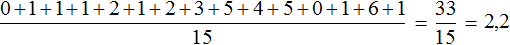Что такое мода в математике 6 класс

Мода (математика)

Мода — значение во множестве наблюдений, которое встречается наиболее часто. Иногда в совокупности встречается более чем одна мода (например: 2, 6, 6, 6, 8, 9, 9, 9, 10; мода = 6 и 9). В этом случае можно сказать, что совокупность мультимодальна. Из структурных средних величин только мода обладает таким уникальным свойством. Как правило мультимодальность указывает на то, что набор данных не подчиняется нормальному распределению.

Мода, как средняя величина, употребляется чаще для данных, имеющих нечисловую природу. Среди перечисленных цветов автомобилей — белый, черный, синий металлик, белый, синий металлик, белый — мода будет равна белому цвету. При экспертной оценке с её помощью определяют наиболее популярные типы продукта, что учитывается при прогнозе продаж или планировании их производства.

См.также

Смотреть что такое «Мода (математика)» в других словарях:

МАТЕМАТИКА — Математику обычно определяют, перечисляя названия некоторых из ее традиционных разделов. Прежде всего, это арифметика, которая занимается изучением чисел, отношений между ними и правил действий над числами. Факты арифметики допускают различные… … Энциклопедия Кольера

Портрет итальянского Ренессанса — Сандро Боттичелли. «Портрет юноши с медалью Козимо Медичи». 1470 1477. Уффици, Флоренция Портрет итальянского … Википедия

Среднее арифметическое — У этого термина существуют и другие значения, см. среднее значение. В математике и статистике среднее арифметическое одна из наиболее распространённых мер центральной тенденции, представляющая собой сумму всех наблюденных значений деленную на их… … Википедия

Друга Ріка — (рус. Вторая Река) украинская поп рок группа созданная в начале 1996 года в городе Житомире, Украина Друга Ріка Жанр Поп рок Годы с … Википедия

Миланский технический университет — Оригинальное название итал. Politecnico di Milano Прежние названия итал. … Википедия

Успенский, Яков Викторович — Яков Викторович Успенский Дата рождения: 29 апреля (11 мая) 1883(1883 05 11) Место рождения: Урга, Внешняя Монголия, Империя Цин Дата смерти: 27 января … Википедия

Флоренция* — (итал. Firenze, прежде Fiorenza, лат. Florentia цветущий город ) главный город провинции Ф., до 1859 г. главный город Тосканского великого герцогства, с 1865 до 1871 г. столица Итальянского королевства, под 43°46 с. ш. и 11°17 в. д. от Гринвича,… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

Флоренция, город — (итал. Firenze, прежде Fiorenza, лат. Florentia цветущий город ) гл. гор. провинции Ф., до 1859 г. гл. гор. Тосканского великого герцогства, с 1865 до 1871 г. столица Итальянского королевства, под 43° 46 с. ш. и 11° 17 в. д. от Грин., на высоте,… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

Сейлор Мун — Главная героиня аниме «Сейлор Мун», Усаги Цукино Sailor Moon (англ.) яп. 美少女戦士セーラームーン … Википедия

Египет — I (греч. Αϊγυπτος; лат. Aegyptus; фр. Egypte; англ. Egypt; нем. Aegypten; итал. Egytto; арабск. Masz). Положение, границы. Страна Е. (в узком, историческом смысле слова) лежит между 24°5 и 31°35 северной широты и 28°50 и 34°41 восточной долготы… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

Источник

Что такое мода в математике 6 класс

Калькулятор вычислит среднее арифметическое чисел, а также размах ряда чисел, моду ряда чисел, медиану ряда. Для вычисления укажите количество чисел, добавьте числа и нажмите рассчитать.

Среднее арифметическое, размах, мода и медиана

Средним арифметическим ряда чисел называется частное от деления суммы этих чисел на число слагаемых.

Для ряда a₁,a₁. a_n среднее арифметическое вычисляется по формуле:

Найдем среднее арифметическое для чисел 5,24, 6,97, 8,56, 7,32 и 6,23.

Размахом ряда чисел называется разность между наибольшим и наименьшим из этих чисел.

Размах ряда 5,24, 6,97, 8,56, 7,32, 6,23 равен 8,56-5,24=3.32

Модой ряда чисел называется число, которое встречается в данном ряду чаще других.

Ряд чисел может иметь более одной моды, а может не иметь моды совсем.

Модой ряда 32, 26, 18, 26, 15, 21, 26 является число 26, встречается 3 раза.

В ряду чисел 5,24, 6,97, 8,56, 7,32 и 6,23 моды нет.

Ряд 1, 1, 2, 2, 3 содержит 2 моды: 1 и 2.

Медианой упорядоченного ряда чисел с нечётным числом членов называется число, записанное посередине, а медианой упорядоченного ряда чисел с чётным числом членов называется среднее арифметическое двух чисел, записанных посередине.

Медианой произвольного ряда чисел называется медиана соответствующего упорядоченного ряда.

Медиана ряда 4, 1, 2, 3, 3, 1 равна 2.5.

Примеры

Рассмотрим примеры нахождения среднего арифметического чисел, а также размаха, медианы и моды ряда.

Источник

Среднее арифметическое чисел. Мода. Медиана. Размах ряда чисел

Среднее арифметическое нескольких величин – это отношение суммы величин к их количеству.

Правило. Чтобы вычислить среднее арифметическое нескольких чисел, нужно взять сумму этих чисел и разделить все на количество слагаемых. Частное и будет средним арифметическим этих чисел.

Например: найдем среднее арифметическое чисел 2; 6; 9; 15.

У нас четыре числа, значит надо их сумму разделить на четыре. Это и будет среднее арифметическое данных чисел: (2 + 6 + 9 + 15) : 4 = 8.

Размах ряда чисел – это разность между наибольшим и наименьшим из этих чисел.

Например: найдем размах чисел 2; 5; 8; 12; 33.

Наибольшее число здесь – 33, наименьшее – 2. Значит, размах составляет 31, т. е.: 33 – 2 = 31.

Мода ряда чисел – это число, которое встречается в данном ряду чаще других.

Например: найдем моду ряда чисел 1; 7; 3; 8; 7; 12; 22; 7; 11; 22; 8.

Чаще всего в этом ряде чисел встречается число 7 (3 раза). Оно и является модой данного ряда чисел.

Медианой упорядоченного ряда чисел с нечетным числом членов называется число, записанное посередине, а медианой упорядоченного ряда чисел с четным числом членов называется среднее арифметическое двух чисел, записанных посередине.

Медианой произвольного ряда чисел называется медиана соответствующего упорядоченного ряда.

Например: в ряде чисел 2; 5; 9; 15; 21 медианой является число 9, находящееся посередине.

Найдем медиану в ряде чисел 4; 5; 7; 11; 13; 19.

Здесь четное количество чисел (6). Поэтому ищем не одно, а два числа, записанных посередине. Это числа 7 и 11. Находим среднее арифметическое этих чисел: (7 + 11) : 2 = 9. Число 9 является медианой данного ряда чисел.

В институте сдавали зачет по высшей математике. В группе было 10 человек, и они получили соответствующие оценки: 3; 5; 5; 4; 4; 4; 3; 2; 4; 5.

Какую оценку получали чаще всего? Каков средний балл сдавшей зачет группы?

Дан ряд чисел: 175; 172; 179; 171; 174; 170; 172; 169.

Найдите медиану и размах ряда.

Дан ряд чисел: 175; 172; 179; 171; 174; 170; 172; 169.

Найдите моду ряда и среднее арифметическое ряда.

Имеются следующие данные о месячной заработной плате пяти рабочих (тг): 126000; 138000; 132000; 141000; 150000.

Найдите среднюю заработную плату.

Магазин продает 8 видов булочек по следующим ценам: 31; 22; 24; 27; 30; 36; 19; 27.

Найдите разность среднего арифметического и медианы этого набора.

Найдите объем и медиану числового ряда.

Товарные запасы хлопчатобумажных тканей в магазине за первое полугодие составили (тыс. тг) на начало каждого месяца:

Определите средний товарный запас хлопчатобумажных тканей за первое полугодие.

Провели несколько измерений случайной величины: 2,5; 2,2; 2; 2,4; 2,9; 1,8.

Найдите среднее арифметическое этого набора чисел.

Провели несколько измерений случайной величины: 6; 18; 17; 14; 4; 22.

Найдите медиану этого набора чисел.

Провели несколько измерений случайной величины:

800; 3200; 2000; 2600; 2900; 2000. Найдите моду этого набора чисел.

Магазин продает 8 видов хлеба по следующим ценам: 60, 75, 80, 85, 90, 100, 110, 120 тенге.

Найдите разность среднего арифметического и медианы этого набора.

Дан числовой ряд: 1; 7; 3; 8; 7; 12; 22; 7; 11; 22; 7,8.

Найдите среднее арифметическое, размах и моду.

Источник

Элементы статистики

Продолжаем изучать элементарные задачи по математике. Сегодня мы поговорим о статистике.

Статистика — это раздел математики в котором изучаются вопросы сбора, измерения и анализа информации, представленной в числовой форме. Происходит слово статистика от латинского слова status (состояние или положение дел).

Так, с помощью статистики мы можем узнать свое положение дел, касающихся финансов. С начала месяца можно вести дневник расходов и по окончании месяца, воспользовавшись статистикой, узнать сколько денег в среднем мы тратили каждый день или какая потраченная сумма была наибольшей в этом месяце либо узнать какую сумму мы тратили наиболее часто.

На основе этой информации можно провести анализ и сделать определенные выводы: следует ли в следующем месяце немного сбавить аппетит, чтобы тратить меньше денег, либо наоборот позволить себе не только хлеб с водой, но и колбасу.

Выборка. Объем. Размах

Что такое выборка? Если говорить простым языком, то это отобранная нами информация для исследования. Например, мы можем сформировать следующую выборку — суммы денег, потраченных в каждый из шести дней. Давайте нарисуем таблицу в которую занесем расходы за шесть дней

Выборка состоит из n-элементов. Вместо переменной n может стоять любое число. У нас имеется шесть элементов, поэтому переменная n равна 6

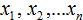
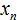
Элементы выборки обозначаются с помощью переменных с индексами . Последний элемент является шестым элементом выборки, поэтому вместо n будет стоять число 6.

Обозначим элементы нашей выборки через переменные

Количество элементов выборки называют объемом выборки. В нашем случае объем равен шести.

Размахом выборки называют разницу между самым большим и маленьким элементом выборки.

Среднее арифметическое

Понятие среднего значения часто используется в повседневной жизни.

Речь идет о среднем арифметическом — результате деления суммы элементов выборки на их количество.

Среднее арифметическое — это результат деления суммы элементов выборки на их количество.

Вернемся к нашему примеру

Узнаем сколько в среднем мы тратили в каждом из шести дней:

Средняя скорость движения

При изучении задач на движение мы определяли скорость движения следующим образом: делили пройденное расстояние на время. Но тогда подразумевалось, что тело движется с постоянной скоростью, которая не менялась на протяжении всего пути.

В реальности, это происходит довольно редко или не происходит совсем. Тело, как правило, движется с различной скоростью.

Когда мы ездим на автомобиле или велосипеде, наша скорость часто меняется. Когда впереди нас помехи, нам приходиться сбавлять скорость. Когда же трасса свободна, мы ускоряемся. При этом за время нашего ускорения скорость изменяется несколько раз.

Речь идет о средней скорости движения. Чтобы её определить нужно сложить скорости движения, которые были в каждом часе/минуте/секунде и результат разделить на время движения.

Задача 1. Автомобиль первые 3 часа двигался со скоростью 66,2 км/ч, а следующие 2 часа — со скоростью 78,4 км/ч. С какой средней скоростью он ехал?

Сложим скорости, которые были у автомобиля в каждом часе и разделим на время движения (5ч)

Значит автомобиль ехал со средней скоростью 71,08 км/ч.

Определять среднюю скорость можно и по другому — сначала найти расстояния, пройденные с одной скоростью, затем сложить эти расстояния и результат разделить на время. На рисунке видно, что первые три часа скорость у автомобиля не менялась. Тогда можно найти расстояние, пройденное за три часа:

Аналогично можно определить расстояние, которое было пройдено со скоростью 78,4 км/ч. В задаче сказано, что с такой скоростью автомобиль двигался 2 часа:

Сложим эти расстояния и результат разделим на 5

Задача 2. Велосипедист за первый час проехал 12,6 км, а в следующие 2 часа он ехал со скоростью 13,5 км/ч. Определить среднюю скорость велосипедиста.

Скорость велосипедиста в первый час составляла 12,6 км/ч. Во второй и третий час он ехал со скоростью 13,5. Определим среднюю скорость движения велосипедиста:

Мода и медиана

Модой называют элемент, который встречается в выборке чаще других.

Рассмотрим следующую выборку: шестеро спортсменов, а также время в секундах за которое они пробегают 100 метров

Элемент 14 встречается в выборке чаще других, поэтому элемент 14 назовем модой.

Рассмотрим еще одну выборку. Тех же спортсменов, а также смартфоны, которые им принадлежат

Элемент iphone встречается в выборке чаще других, значит элемент iphone является модой. Говоря простым языком, носить iphone модно.

Конечно элементы выборки в этот раз выражены не числами, а другими объектами (смартфонами), но для общего представления о моде этот пример вполне приемлем.

Рассмотрим следующую выборку: семеро спортсменов, а также их рост в сантиметрах:

Упорядочим данные в таблице так, чтобы рост спортсменов шел по возрастанию. Другими словами, построим спортсменов по росту:

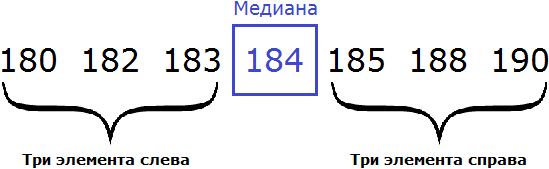
Выпишем рост спортсменов отдельно:

В получившейся выборке 7 элементов. Посередине этой выборки располагается элемент 184. Слева и справа от него по три элемента. Такой элемент как 184 называют медианой упорядоченной выборки.

Медианой упорядоченной выборки называют элемент, располагающийся посередине.

Отметим, что данное определение справедливо в случае, если количество элементов упорядоченной выборки является нечётным.

В рассмотренном выше примере, количество элементов упорядоченной выборки было нечётным. Это позволило нам быстро указать медиану

Но возможны случаи, когда количество элементов выборки чётно.

К примеру, рассмотрим выборку в которой не семеро спортсменов, а шестеро:

Построим этих шестерых спортсменов по росту:

Выпишем рост спортсменов отдельно:

180, 182, 184, 186, 188, 190

В данной выборке не получается указать элемент, который находился бы посередине. Если указать элемент 184 как медиану, то слева от этого элемента будут располагаться два элемента, а справа — три. Если как медиану указать элемент 186, то слева от этого элемента будут располагаться три элемента, а справа — два.

В таких случаях для определения медианы выборки, нужно взять два элемента выборки, находящихся посередине и найти их среднее арифметическое. Полученный результат будет являться медианой.

Вернемся к нашим спортсменам. В упорядоченной выборке 180, 182, 184, 186, 188, 190 посередине располагаются элементы 184 и 186

Найдем среднее арифметическое элементов 184 и 186

Элемент 185 является медианой выборки, несмотря на то, что этот элемент не является членом исходной и упорядоченной выборки. Спортсмена с ростом 185 нет среди остальных спортсменов. Рост в 185 см используется в данном случае для статистики, чтобы можно было сказать о том, что срединный рост спортсменов составляет 185 см.

Поэтому более точное определение медианы зависит от количества элементов в выборке.

Если количество элементов упорядоченной выборки нечётно, то медианой выборки называют элемент, располагающийся посередине.

Если количество элементов упорядоченной выборки чётно, то медианой выборки называют среднее арифметическое двух чисел, располагающихся посередине этой выборки.

Медиана и среднее арифметическое по сути являются «близкими родственниками», поскольку и то и другое используют для определения среднего значения. Например, для предыдущей упорядоченной выборки 180, 182, 184, 186, 188, 190 мы определили медиану, равную 185. Этот же результат можно получить путем определения среднего арифметического элементов 180, 182, 184, 186, 188, 190

Но медиана в некоторых случаях отражает более реальную ситуацию. Например, рассмотрим следующий пример:

Было подсчитано количество имеющихся очков у каждого спортсмена. В результате получилась следующая выборка:

0, 1, 1, 1, 2, 1, 2, 3, 5, 4, 5, 0, 1, 6, 1

Определим среднее арифметическое для данной выборки — получим значение 2,2

По данному значению можно сказать, что в среднем у спортсменов 2,2 очка

Теперь определим медиану для этой же выборки. Упорядочим элементы выборки и укажем элемент, находящийся посередине:

В данном примере медиана лучше отражает реальную ситуацию, поскольку половина спортсменов имеет не более одного очка.

Частота

Частота это число, которое показывает сколько раз в выборке встречается тот или иной элемент.

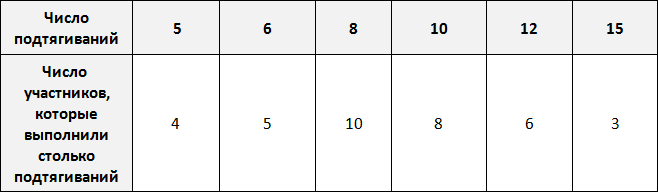
Предположим, что в школе проходят соревнования по подтягиваниям. В соревнованиях участвует 36 школьников. Составим таблицу в которую будем заносить число подтягиваний, а также число участников, которые выполнили столько подтягиваний.

По таблице можно узнать сколько человек выполнило 5, 10 или 15 подтягиваний. Так, 5 подтягиваний выполнили четыре человека, 10 подтягиваний выполнили восемь человек, 15 подтягиваний выполнили три человека.

Количество человек, повторяющих одно и то же число подтягиваний в данном случае являются частотой. Поэтому вторую строку таблицы переименуем в название «частота»:

Такие таблицы называют таблицами частот.

Частота обладает следующим свойством: сумма частот равна общему числу данных в выборке.

Это означает, что сумма частот равна общему числу школьников, участвующих в соревнованиях, то есть тридцати шести. Проверим так ли это. Сложим частоты, приведенные в таблице:

4 + 5 + 10 + 8 + 6 + 3 = 36

Относительная частота

Относительная частота это в принципе та же самая частота, которая была рассмотрена ранее, но только выраженная в процентах.

Относительная частота равна отношению частоты на общее число элементов выборки.

Вернемся к нашей таблице:

Пять подтягиваний выполнили 4 человека из 36. Шесть подтягиваний выполнили 5 человек из 36. Восемь подтягиваний выполнили 10 человек из 36 и так далее. Давайте заполним таблицу с помощью таких отношений:

Выполним деление в этих дробях:

Выразим эти частоты в процентах. Для этого умножим их на 100. Умножение на 100 удобно выполнить передвижением запятой на две цифры вправо:

Теперь можно сказать, что пять подтягиваний выполнили 11% участников, 6 подтягиваний выполнили 14% участников, 8 подтягиваний выполнили 28% участников и так далее.

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

42 thoughts on “Элементы статистики”

Спасибо, что вы вернулись.
Будут ли новые уроки?

Источник