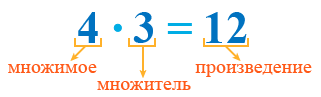Что такое множитель и произведение в математике
Что такое множитель
Под множителем в математике понимают любое число, на которое заданное делится без остатка. То есть это то число, которое показывает сколько именно раз повторить в качестве слагаемого другое число, которое называют множимым. Результат таких математических исчислений называют произведением. Если множителей в примере несколько, то они нумеруются и называются, соответственно, «первый множитель», «второй» и т.д.
Понятие «множитель» существует и в физике, где оно применяется в качестве составной части сложных формул. Так, Ланде множитель – это составная часть в формуле для расщепления уровней энергии в магнитном поле.
Высшая математика использует понятие «интегрирующий множитель», т.е. это величина, после умножения на которую часть дифференциального уравнения обращается в полный дифференциал некоторой функции.
В экономической теории есть понятие дисконтирующего множителя, введенное англичанами (discounting multiplier) в качестве расчетного показателя при оценке долгосрочных денежных операций. В частности, с его помощью определяется величина инвестируемой сегодня используют и страховые компании, и аудиторы в оценках перспективности проектов, анализе затрат и инвестиционных рисков.
Из математики «множитель» позаимствован и специалистами в области линейного программирования, которые используют множители Лагранжа (Lagrange multipliers) для проверки оптимальности допустимого решения целевой функции. Обозначается он греческой буквой «лямбда» и применяется при решении в основном теоретизированных задач на условный экстремум.
Умножение
В этом разделе познакомимся с умножением и узнаем, что сложение одинаковых слагаемых можно заменить умножением.
Например, 6 + 6 + 6 + 6 = 24 можно записать по-другому: 6 • 4 = 24
Смысл действия умножения состоит в том, что при умножении находится сумма одинаковых слагаемых.
Первое число при умножении показывает, какое слагаемое повторяют несколько раз.
Второе число при умножении показывает, сколько раз повторяют это слагаемое.
Результат умножения показывает, какое число получается.
6 • 4 значит, что число 6 повторяют 4 раза: 6 + 6 + 6 + 6 = 24
Числа при умножении
Результат умножения, или Произведение
Чтение числовых выражений
Этот пример можно прочитать по-разному.
Умножение на 1
4 • 1 = 4, потому что это значит, что число 4 повторяют только 1 раз.
23 • 1 = 23, потому что это значит, что число 23 повторяют только 1 раз.
Умножение на 0
8 • 0 = 0, потому что это значит, что число 8 повторяют 0 раз.
26 • 0 = 0, потому что это значит, что число 26 повторяют 0 раз.
Умножение на 10
8 • 10 = 80, потому что число 8 повторяют 10 раз.
15 • 10 = 150, потому что число 15 повторяют 10 раз.
Связь деления и умножения
8 • 3 = 24, потому что 8 повторяют 3 раза.
24 : 3 = 8, потому что в 24 по 3 содержится 8 раз.
24 : 8 = 3, потому что в 24 по 8 содержится 3 раза.
В несколько раз больше
Решим задачу:
В магазине было 2 лисички, а котят в 4 раза больше. Сколько было котят?
Это значит, что котят было 4 раза по 2.
Заменяем сложение умножением и получаем:
Во сколько раз больше? Во сколько раз меньше?
Например, решим задачу: В магазине было 8 котят и 2 лисички. Во сколько раз котят было больше, чем лисичек? Во сколько раз лисичек было меньше, чем котят?
Чтобы ответить на эти вопросы, нужно узнать, сколько раз по 2 содержится в 8?
Значит, котят в 4 раза больше, чем лисичек, а лисичек в 4 раза меньше, чем котят.
Поделись с друзьями в социальных сетях:
Числа. Произведение чисел. Свойства умножения.
Умножение — одно из четырёх основных арифметических действий, бинарная математическая операция, в которой один аргумент складывается столько раз, сколько показывает другой.
Произведение чисел m и n — это сумма n слагаемых, каждое из этих слагаемых = m.
Выражение типа m • n, и значение такого выражения называется произведение чисел m и n. Числа m и n называются множителями.
Если устное умножение чисел затруднительно используют умножение в столбик. В столбик можно умножать большие натуральные числа или десятичные дроби.
Свойства умножения чисел.
1. Коммутативность: 
При перестановке множителей местами, значение произведения остается без изменений. Это переместительное свойство умножения.
где, 3 и 4 — множители, а 12 — произведение.
2. Ассоциативность: 
В произведении 3-х и больше множителей при перестановке этих множителей либо изменения последовательности выполнения умножения результат остается одинаковым.
3. Дистрибутивность: 
4. Произведение всякого натурального числа и единицы, будет соответствовать этому числу.
Произведение всякого натурального числа и нуля, = 0.
Выражения с буквенными множителями записывают так:
Кроме того, не используют знак умножения и перед скобками,
2 • (a + b) записывают как 2(а + b),
Что такое множитель и разложение на простые множители
Дадим определение понятию «множитель» и разберемся что такое множитель. Какие множители бывают и почему некоторые из множителей — простые.
Определение множителя
В младших классах вы учили, что множители — это числа, которые мы умножаем, называя результат их умножения произведением.
Определения множителя как компонента умножения
Сейчас немного расширим понятие множителя.
Давайте рассмотрим определение множителя на примерах. Давайте определим где в представлении числа или выражения прячется множитель?
Пример 1
Пусть нам дано число 15. Это число можно представить в виде произведения 
. Значит, согласно определению 5 — это множитель, 3 — это тоже множитель.
Пример 2
Рассмотрим теперь выражение: 
. Это выражение можно представить в виде произведения 
. Получаем два множителя — первый множитель (2x-3) и второй множитель (2x+3).
Самое простое произведение имеет два множителя, но может быть и больше множителей.
Простые множители
Пример 1
Разложите число 65 на простые множители.
Решение: число 65 будем делить на простые числа, пока оно нацело не разделится. Так мы видим, что число 65 не делится на 2, 3 и 4, так как не соответствует признакам делимости на эти числа. Зато делится на 5, так как оканчивается на 5. При делении мы получаем 13. Число 13 — простое, так как делится только на себя и на единицу. Таким образом, число 
. И мы выполнили разложение числа на простые множители. Теперь вы знаете, как разложить число на простые множители.
Пример 2
Разложите число 270 на простые множители.
Решение: Разделим сначала число 270 на 2 (сначала берем самое маленькое простое число), получим 135. Посмотрим, делится ли это число на 3. Для этого сложим все числа, стоящие в разрядах данного числа — 
. Девять делится на 3, значит, и число 135 разделится на 3: 
. Получившееся число опять делится на 3: 
. И снова число 15 делится на 3: 
. Получили простое число 5. Делим 
.
Итак, запишем разложение числа 270 на простые множители в виде столбца, где справа от черты мы пишем на какое простое число мы делим, а слева — что получаем:
Разложение числа на простые множители в столбик.
Разложение числа на простые множители в строчку записывается так: 
.
Про разложение многочлена на множители поговорим в отдельной теме.
Умножение натуральных чисел
Умножение — это арифметическое действие, с помощью которого находят сумму одинаковых слагаемых.
Пример. Во дворе посадили 3 ряда ёлок, по 4 ёлки в каждом ряду. Сколько ёлок посадили во дворе?
Чтобы ответить на этот вопрос, надо найти сумму 3 слагаемых, каждое из которых равно 4.
Складывая 3 раза по 4 ёлки, мы получим общее количество ёлок во всех трёх рядах.
Умножить – значит повторить одно число слагаемым столько раз, сколько в другом содержится единиц.
Для записи умножения используется знак х (косой крест) или · (точка), который ставится между числами. Например:
Эта запись означает, что 4 надо умножить на 3. Справа от записи умножения ставится знак = (равно), после которого записывается полученный результат:
Умножение – это краткая запись сложения одинаковых слагаемых.
Пример. Умножить 6 на 5 — это значит найти сумму пяти слагаемых, каждое из которых равно шести:
Сократим запись, заменив сложение на умножение:
Оба выражения равны:
6 + 6 + 6 + 6 + 6 = 6 · 5 = 30,
но для краткости записей лучше всегда использовать умножение, когда число одинаковых слагаемых больше двух.
Множимое, множитель и произведение
Множимое — это число, которое умножают. Множитель — это число, на которое умножают. Например, в записи:
4 — это множимое, 3 — множитель. Множимое является числом, которое выступает в качестве слагаемого. Множитель — это число, которое указывает количество одинаковых слагаемых.
Произведение — это число, которое получается в результате умножения. Например, в записи:
12 — это произведение. При этом сама запись 4 · 3 тоже называется произведением.
Множимое и множитель иначе называются множителями или сомножителями.
Проверка умножения
Умножение двух чисел можно проверить делением, для этого произведение делят на один из сомножителей, если частное окажется равно другому сомножителю, то умножение выполнено верно.