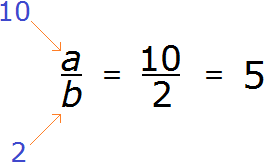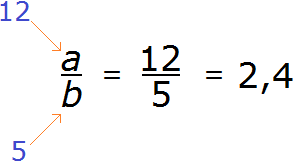Что такое множество целых чисел

Какие числа называются целыми

Определение целых чисел

Что важно знать о целых числах:

Целые числа на числовой оси выглядят так:

На координатной прямой начало отсчета всегда начинается с точки 0. Слева находятся все отрицательные целые числа, справа — положительные. Каждой точке соответствует единственное целое число.

В любую точку прямой, координатой которой является целое число, можно попасть, если отложить от начала координат данное количество единичных отрезков.

Натуральные числа — это целые, положительные числа, которые мы используем для подсчета. Вот они: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 + ∞.

Целые числа — это расширенное множество натуральных чисел, которое можно получить, если добавить к ним нуль и противоположные натуральным отрицательные числа. Множество целых чисел обозначают Z.

Выглядит эти ребята вот так:

Последовательность целых чисел можно записать так:

Свойства целых чисел

Таблица содержит основные свойства сложения и умножения для любых целых a, b и c:

Источник

Целые числа: общее представление

В данной статье определим множество целых чисел, рассмотрим, какие целые называются положительными, а какие отрицательными. Также покажем, как целые числа используются для описания изменения некоторых величин. Начнем с определения и примеров целых чисел.

Целые числа. Определение, примеры

Определение 1. Целые числа

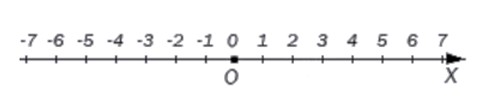
Целые числа и координатная прямая

Пусть координатная прямая проведена горизонтально и направлена вправо. Взглянем на нее, чтобы наглядно представить расположение целых чисел на прямой.

В любую точку прямой, координатой которой является целое число, можно попасть, отложив от начала координат некоторое количество единичных отрезков.

Положительные и отрицательные целые числа

Из всех целых чисел логично выделить положительные и отрицательные целые числа. Дадим их определения.

Определение 2. Положительные целые числа

Определение 3. Отрицательные целые числа

Число 0 разделяет положительные и отрицательные целые числа и само не является ни положительным, ни отрицательным.

Любое число, противоположное положительному целому числу, в силу определения, является отрицательным целым числом. Справедливо и обратное. Число, обратное любому отрицательному целому числу, есть положительное целое число.

Можно дать другие формулировки определений отрицательных и положительных целых чисел, используя их сравнение с нулем.

Определение 4. Положительные целые числа

Соответственно, положительные числа лежат правее начала отсчета на координатной прямой, а отрицательные целые числа находятся левее от нуля.

Неположительные и неотрицательные целые числа

Определение 6. Неотрицательные целые числа

Как видим, число нуль не является ни положительным, ни отрицательным.

Использование целых чисел при описании изменения величин

Для чего используются целые числа? В первую очередь, с их помощью удобно описывать и определять изменение количества каких-либо предметов. Приведем пример.

Пусть на складе хранится какое-то количество коленвалов. Если на склад привезут еще 500 коленвалов, то их количество увеличится. Число 500 как раз и выражает изменение (увеличение) количества деталей. Если потом со склада увезут 200 деталей, то это число также будет характеризовать изменение количества коленвалов. На этот раз, в сторону уменьшения.

Если же со склада ничего не будут забирать, и ничего не будут привозить, то число 0 укажет на неизменность количества деталей.

Очевидное удобство использования целых чисел в отличие от натуральных в том, что их знак явно указывает на направление изменения величины (увеличение или убывание).

Источник

Числа. Целые числа. Свойства целых чисел.

Целые числа – это натуральные числа, а также противоположные им числа и нуль.

Целые числа — расширение множества натуральных чисел N, которое получается путем добавления к N 0 и отрицательных чисел типа − n. Множество целых чисел обозначают Z.

Сумма, разность и произведение целых чисел дают снова целые числа, т.е. целые числа составляют кольцо относительно операций сложения и умножения.

Целые числа на числовой оси:

Сколько целых чисел? Какое количество целых чисел? Самого большого и самого маленького целого числа нет. Этот ряд бесконечен. Наибольшее и наименьшее целое число не существует.

Натуральные числа еще называются положительными целыми числами, т.е. фраза «натуральное число» и «положительное целое число» это одно и то же.

Ни обыкновенные, ни десятичные дроби не являются целыми числами. Но существуют дроби с целыми числами.

Операции над целыми числами.

1. Сумма целых чисел.

Для сложения двух целых чисел с одинаковыми знаками, необходимо сложить модули этих чисел и перед суммой поставить итоговый знак.

2. Вычитание целых чисел.

Для сложения двух целых чисел с разными знаками, необходимо из модуля числа, которое больше вычесть модуль числа, которое меньше и перед ответом поставить знак большего числа по модулю.

3. Умножение целых чисел.

Для умножения двух целых чисел, необходимо перемножить модули этих чисел и перед произведением поставить знак плюс (+), если исходные числа были одного знака, и минус (–) – если разного.

Когда умножаются несколько чисел, знак произведения будет положительным, если число неположительных сомножителей чётное, и отрицателен, если нечётное.

(–2) ∙ (+3) ∙ (–5) ∙ (–3) ∙ (+4) = –360 (3 неположительных сомножителя).

4. Деление целых чисел.

Для деления целых чисел, необходимо поделить модуль одного на модуль другого и поставить перед результатом знак «+», если знаки чисел одинаковые, и минус, – если разные.

Свойства целых чисел.

Z не замкнуто относительно деления 2-х целых чисел (например, 1/2). Ниже приведенная таблица показывает некоторые основные свойства сложения и умножения для любых целых a, b и c.

Источник

Что такое множество?

Множество — это набор каких-либо объектов. Объекты, из которых состоит множество, называются элементами этого множества.

В математике множество рассматривается намного шире. Мы не будем сильно углубляться в эту тему, поскольку она относится к высшей математике и на первых порах может создавать трудности для обучения. Мы рассмотрим только ту часть темы, с которой уже имели дело.

Обозначения

Множество чаще всего обозначают заглавными буквами латинского алфавита, а его элементы — строчными. При этом элементы заключаются в фигурные скобки.

Обозначим множество наших друзей через заглавную латинскую букву F ( friends ), затем поставим знак равенства и в фигурных скобках перечислим наших друзей:

Обозначим через любую заглавную латинскую букву данное множество, например, через букву D

затем поставим знак равенства и в фигурных скобках перечислим элементы данного множества, то есть перечислим делители числа 6

Читается как «2 принадлежит множеству делителей числа 6»

Читается как «5 не принадлежит множеству делителей числа 6»

Кроме того, множество можно записывать прямым перечислением элементов, без заглавных букв. Это может быть удобным, если множество состоит из небольшого количества элементов. Например, зададим множество из одного элемента. Пусть этим элементом будет наш друг Том:

Зададим множество, которое состоит из одного числа 2

Зададим множество, которое состоит из двух чисел: 2 и 5

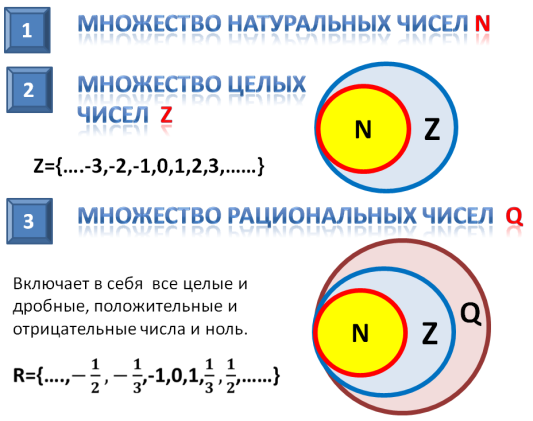
Множество натуральных чисел

Это первое множество с которым мы начали работать. Натуральными числами называют числа 1, 2, 3 и т.д.

Натуральные числа появились из-за потребности людей сосчитать те иные объекты. Например, посчитать количество кур, коров, лошадей. Натуральные числа возникают естественным образом при счёте.

В математике множество натуральных чисел обозначается заглавной латинской буквой N.

Например, укажем, что число 1 принадлежит множеству натуральных чисел. Для этого записываем число 1, затем с помощью знака принадлежности ∈ указываем, что единица принадлежит множеству N

Читается как: «единица принадлежит множеству натуральных чисел»

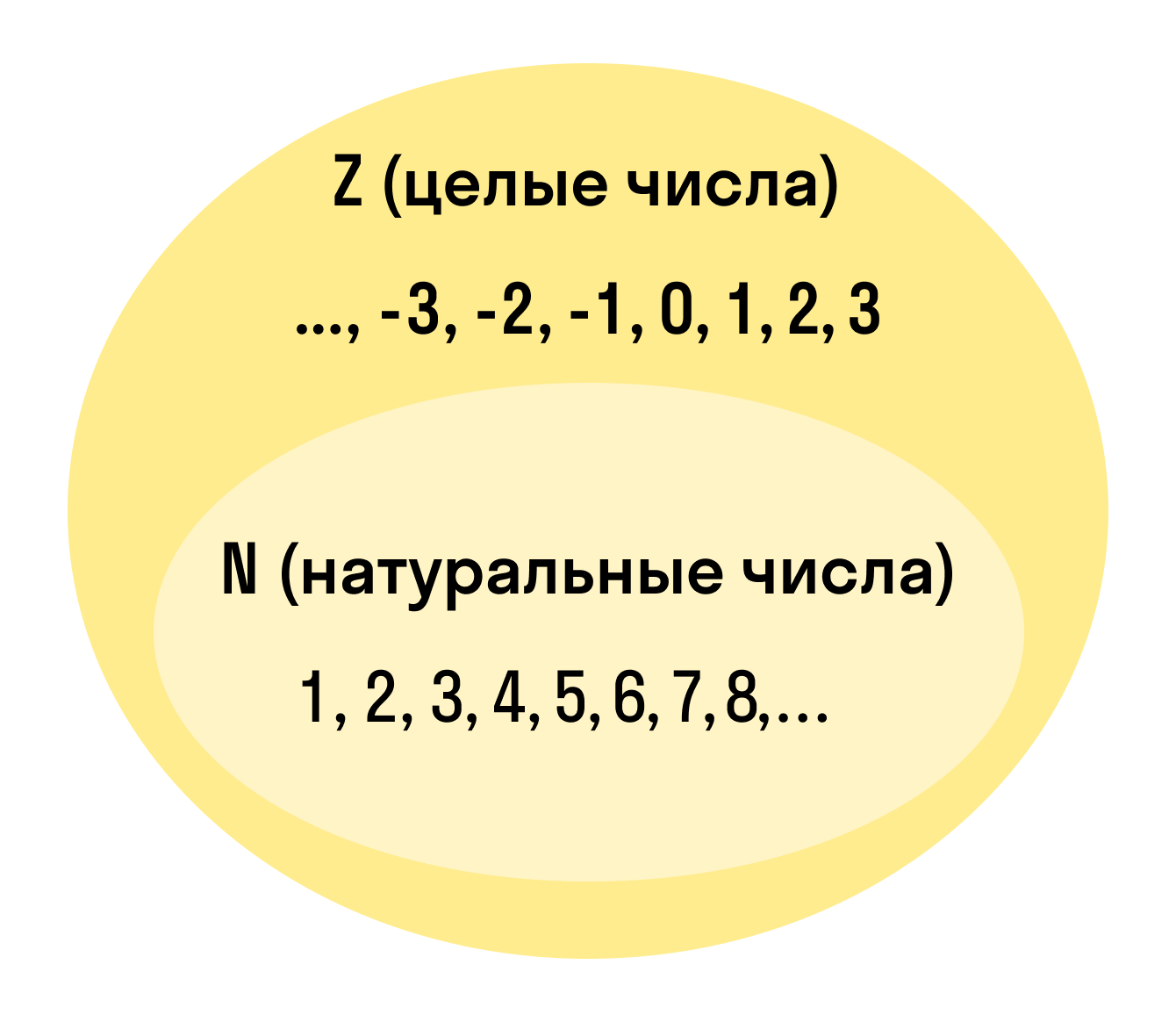
Множество целых чисел

Множество целых чисел включает в себя все положительные и отрицательные числа, а также число 0.

Укажем, к примеру, что число −5 принадлежит множеству целых чисел:

Укажем, что 10 принадлежит множеству целых чисел:

Укажем, что 0 принадлежит множеству целых чисел:

В будущем все положительные и отрицательные числа мы будем называть одним словосочетанием — целые числа.

Множество рациональных чисел

Рациональные числа, это те самые обыкновенные дроби, которые мы изучаем по сей день.

В роли числителя и знаменателя могут быть любые числа, в том числе и целые (за исключением нуля, поскольку на нуль делить нельзя).

Например, представим, что вместо a стоит число 10, а вместо b — число 2

10 разделить на 2 равно 5. Видим, что число 5 может быть представлено в виде дроби 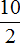, а значит число 5 входит во множество рациональных чисел.

Легко заметить, что число 5 также относится и ко множеству целых чисел. Стало быть множество целых чисел входит во множество рациональных чисел. А значит, во множество рациональных чисел входят не только обыкновенные дроби, но и целые числа вида −2, −1, 0, 1, 2.

Теперь представим, что вместо a стоит число 12, а вместо b — число 5.

12 разделить на 5 равно 2,4. Видим, что десятичная дробь 2,4 может быть представлена в виде дроби 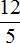, а значит она входит во множество рациональных чисел. Отсюда делаем вывод, что во множество рациональных чисел входят не только обыкновенные дроби и целые числа, но и десятичные дроби.

Мы вычислили дробь 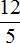и получили ответ 2,4. Но мы могли бы выделить в этой дроби целую часть:

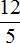
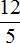
При выделении целой части в дроби , получается смешанное число . Видим, что смешанное число тоже может быть представлено в виде дроби . Значит во множество рациональных чисел входят и смешанные числа.

В итоге мы приходим к выводу, что множество рациональных чисел содержат в себе:

Множество рациональных чисел обозначается заглавной латинской буквой Q.

Например укажем, что дробь принадлежит множеству рациональных чисел. Для этого записываем саму дробь , затем с помощью знака принадлежности ∈ указываем, что дробь принадлежит множеству рациональных чисел:

∈ Q

Укажем, что десятичная дробь 4,5 принадлежит множеству рациональных чисел:

Укажем, что смешанное число 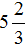принадлежит множеству рациональных чисел:

∈ Q

Вводный урок по множествам завершён. В будущем мы рассмотрим множества намного лучше, а пока рассмотренного в данном уроке будет достаточно.

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

12 thoughts on “Что такое множество?”

Источник

Что такое множество в математике и как оно обозначается

Множество – это количество предметов или чисел, обладающих общими свойствами.

Данное определение подходит к любой совокупности с одинаковыми признаками, независимо оттого, сколько предметов в нее входит: толпа людей, стог сена, звезды в небе.

В математике изучаемое понятие обозначается заглавными латинскими буквами, например: А, С, Z, N, Q, A₁, A₂ и т. д.

Объекты, составляющие группу, называются элементами множества и записываются строчными латинскими буквами: a, b, c, d, x, y, a₁, a₂ и т. д.

Границы совокупности обозначаются фигурными скобками < >.

А = <а, в, с, у>– А состоит из четырех элементов.

Записать совокупность Z согласных букв в слове «калькулятор»:

Z = <к, л, т, р>, повторяющиеся согласные записываются один раз. Z состоит из четырех элементов.

Принадлежность элементов множеству обозначается знаком – Є.

Пример: N = , а Є N – элемент «а» принадлежит N.

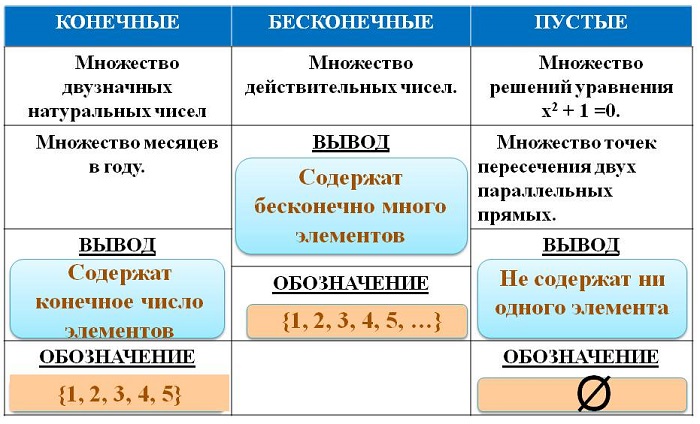
Выделяют три вида множеств:

пустые (обозначаются Ø) – не имеющие элементов.

Пример: А = <а, в, с, у>и В = <а, в, с, е, к>– все элементы А являются элементами совокупности В, следовательно А ⊆ В.

Если множества состоят из одинаковых элементов, их называют равными.

Пример: А = <23, 29, 48>и В = <23, 29, 48>, тогда А = В.

В математике выделяют несколько числовых совокупностей. Рассмотрим их подробнее.

Множество натуральных чисел

Относится ли ноль к натуральным числам? Это до сих пор открытый вопрос для математиков всего мира.

Множество целых чисел

Совокупность целых чисел (Z) включает в себя положительные натуральные и отрицательные числа, а также ноль:

Множество рациональных чисел

Совокупность рациональных чисел (Q) состоит из дробей (обыкновенных и десятичных), целых и смешанных чисел:

Любое рациональное число можно представить в виде дроби, у которой числителем служит любое целое число, а знаменателем – натуральное:

Следовательно, N и Z являются подмножествами Q.

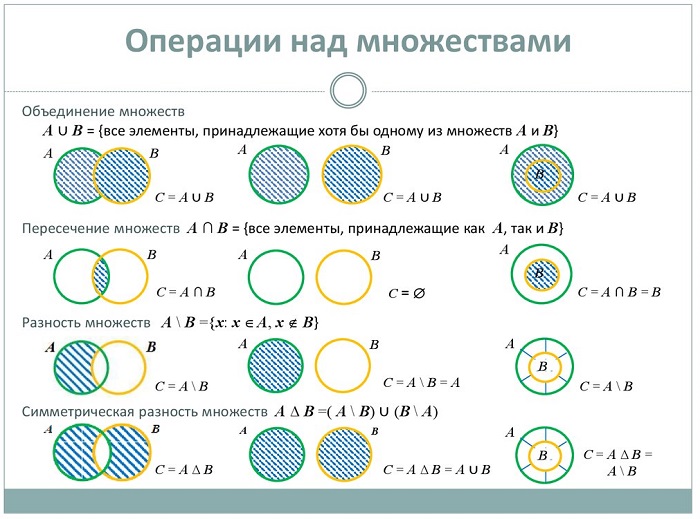
Операции над множествами

Точно так же, как и все математические объекты, множества можно складывать и вычитать, то есть совершать операции.

Если две группы образуют третью, содержащую элементы исходных совокупностей – это называется суммой (объединением) множеств и обозначается знаком ∪.

Если две группы совокупностей образуют третью, состоящую только из общих элементов заданных составляющих, это называется произведением (пересечением) множеств, обозначается значком ∩.

Если две совокупности образуют третью, включающую элементы одной из заданных групп и не содержащую элементы второй, получается разность (дополнение) совокупностей, обозначается значком /.

В случае, когда В / С = С / В, получается симметричная разность и обозначается значком Δ.

Для «чайников» или кому трудно даётся данная тема операции с совокупностями можно отобразить с помощью диаграмм Венна:

Объединение

Пересечение

Дополнение

С помощью данных диаграмм можно разобраться с законами де Моргана по поводу логической интерпретации операций над множествами.

Свойства операций над множествами

Операции над множествами обладают свойствами, аналогичными правилу свойств сложения, умножения и вычитания чисел:

Коммутативность – переместительные законы:

умножения S ∩ D = D ∩ S;

сложения S ∪ D = D ∪ S.

Ассоциативность – сочетательные законы:

умножения (S ∩ F) ∩ G = S ∩ (F ∩ G);

сложения (S ∪ F) ∪ G = S ∪ (F ∪ G).

Дистрибутивность – законы распределения:

умножения относительно вычитания S ∩ (F – G) = (S ∩ F) – (S ∩ G);

умножения относительно сложения G ∩ (S ∪ F) = (G ∩ S) ∪ (G ∩ F);

сложения относительно умножения G ∪ (S ∩ F) = (G ∪ S) ∩ (G ∪ F).

если S ⊆ Fи F ⊆ J, то S ⊆ J;

если S ⊆ F и F ⊆ S, то S = F.

Идемпотентность объединения и пересечения:

О других свойствах операций можно узнать из картинки:

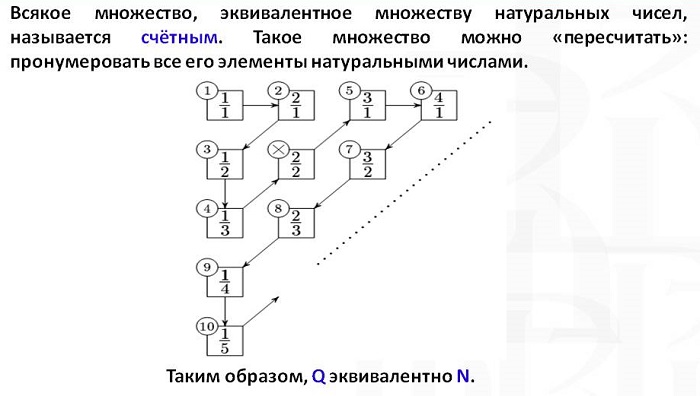
Счетные и несчетные множества

Если между элементами двух групп можно установить взаимное немногозначное соответствие, то эти группы чисел равномощны, при условии равного количества элементов.

Мощность данной математической единицы равна количеству элементов в ней. Например, множество всех нечетных положительных чисел равномощно группе всех четных чисел больше ста.

Но не все группы действительных чисел счетные. Примером несчетной группы предметов является бесконечная десятичная дробь.

Источник