Что такое многогранник в геометрии
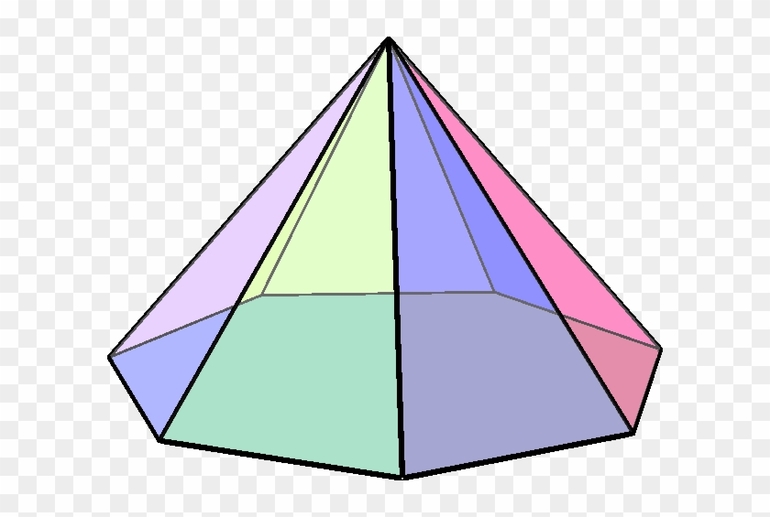
Что такое многогранник? Примеры
Примеры многогранников:
1) каждая сторона одного является одновременно стороной другого (но только одного), называемого смежным с первым (по этой стороне);
Многогранник называется выпуклым, если он лежит по одну сторону от плоскости любой его грани.
Из этого определения следует, что все грани выпуклого многогранника являются плоскими многоугольниками. Поверхность выпуклого многогранника состоит из граней, которые лежат в разных плоскостях. При этом ребрами многогранника являются стороны многоугольников, вершинами многогранника – вершины граней, плоскими углами многогранника – углы многоугольников – граней.
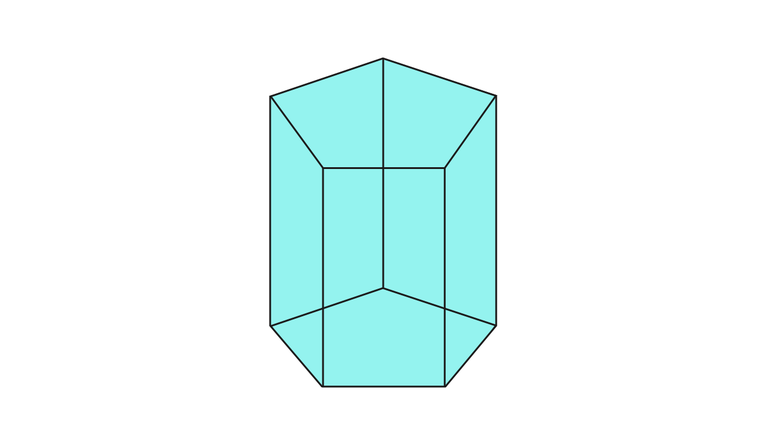
Выпуклый многогранник, все вершины которого лежат в двух параллельных плоскостях, называется призматоидом. Призма, пирамида и усеченная пирамида – частные случаи призматоида. Все боковые грани призматоида являются треугольниками или четырехугольниками, причем четырехугольные грани – это трапеции или параллелограммы.
Популярное
Нам нужны еще фонарики Джека в форме тыквы. Кто же нам поможет? Может быть Архимед?
Почтовые марки охватывают все значимые события в мире. Не обошли вниманием художники-филателисты и изображения многогранников. Почтовая марка, посвященная Леонарду Эйлеру с.
Когда мы готовили 36-ой выпуск «Волшебные грани», у наших коллег возник вопрос: «Почему мы опять собираемся говорить о правильных многогранниках.
Существует концепция, что вершина многогранника отдает энергию, а плоскость энергию принимает. В том случае, если в многограннике вершин больше чем плоскостей, то он обладает.
Лето – это время, которое хочется провести вне помещения. За парту дети сядут в сентябре, а сейчас – все на детскую площадку!
многогранник
Смотреть что такое «многогранник» в других словарях:
многогранник — многогранник … Орфографический словарь-справочник
МНОГОГРАННИК — геометрическое тело, ограниченное со всех сторон плоскими многоугольниками, называемыми гранями. Стороны граней называются ребрами многогранника, а концы ребер вершинами многогранника. По числу граней различают четырехгранники, пятигранники и т.… … Большой Энциклопедический словарь
многогранник — полиэдр, политоп; симплекс Словарь русских синонимов. многогранник сущ. • полиэдр Словарь русских синонимов. Контекст 5.0 Информатик. 2012 … Словарь синонимов
МНОГОГРАННИК — МНОГОГРАННИК, многогранника, муж. (мат.). Геометрическое тело, ограниченное со всех сторон плоскими прямолинейными гранями (треугольниками, четырехугольниками и т.д.). Правильный многогранник. || Такое же тело, ограниченное более, чем четырьмя… … Толковый словарь Ушакова
МНОГОГРАННИК — МНОГОГРАННИК, а, муж. Геометрическое тело, ограниченное со всех сторон плоскими многоугольниками. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова
Многогранник — [polihedron] выпуклое ограниченное множество точек, удовлетворяющих одновременно конечному числу неравенств типа: a11x1 + … + a1nxn ≤ b1 ……………….. am1x1 + … + amnxn ≤ bm или в матричной записи M =… … Экономико-математический словарь
МНОГОГРАННИК — (полиэдр) геометрическое тело, ограниченное плоскими (см.). Правильный М. геометрическая выпуклая поверхность, у которой все грани правильные многоугольники с одним и тем же числом сторон и в каждой вершине многогранника сходится одинаковое… … Большая политехническая энциклопедия
МНОГОГРАННИК — часть пространства, ограниченная совокупностью конечного числа плоских многоугольников (см. ГЕОМЕТРИЯ), соединенных таким образом, что каждая сторона любого многоугольника является стороной ровно одного другого многоугольника (называемого… … Энциклопедия Кольера
Многогранник — В Викисловаре есть статья «многогранник» … Википедия
Основные понятия
Определение многогранника включает в себя такое понятие, как геометрическое тело, созданное из плоских многоугольников. Их число конечное. От формы каждого из них напрямую зависят свойства итоговой фигуры. Их делят на 2 типа:
Поскольку многогранники рассматриваются в трехмерном евклидовом пространстве, они относятся к стереометрии. А их многоугольники лежат в двумерной плоскости, что относится к планиметрии. Поэтому основные свойства и понятия формируются, включая в себя обе эти науки.
Параметры фигуры
Правильные многогранники
Правильные многогранники — фигуры, грани которых представляют собой многоугольники с равными углами и сторонами. Также они называются Платоновыми телами. Всего существует 5 соответствующих тел, подробные характеристики которых представлены в таблице.
Правильные многогранники изучались древними греками. Однако первые модели в орнаменте и по отдельности появились намного раньше. Например, археологами были найдены вырезанные каменные шары в Шотландии, которые датируются поздним неолитом (соответственно, за 1000 лет до жизни и деятельности Платона).
Призма и ее особенности
Геометрическое тело называют прямым, если каждое ребро лежит перпендикулярно основанию. Также они становятся высотами. Когда грани идентичны, многоугольник считается правильным, и его диагональное сечение образует параллелограмм.
Характеристики параллелепипеда
Параллелепипед — многогранник, основанием и гранями которого является параллелограмм. Фигура характеризуется как неправильная. Основные характеристики:
Когда все грани параллелограмма являются прямоугольными, фигура характеризуется, как прямоугольная. Длина каждого ребра считается линейным размером. У такой фигуры есть три измерения. При этом справедлива формула d² = a² + b² + c². При расчетах руководствуются и другими. Для объема : V = abc, для площади многогранника: S=2·(ab+ bc +ac).
Пирамида и ее величины
Пирамида представляет собой многогранник и многоугольник. Особенности фигуры:
Если пирамиду разделяет плоскость, параллельная нижней, она делит ее на две части. Причем верхняя пропорционально равна главной фигуре. Когда основанием является квадрат, геометрическое тело называется правильным. Гранями ее считаются равнобедренные треугольники.
Геометрия. 10 класс
Конспект урока
Геометрия, 10 класс
Урок № 13. Многогранники
Перечень вопросов, рассматриваемых в теме:
Многогранник – геометрическое тело, ограниченное конечным числом плоских многоугольников.
Грани многогранника – многоугольники, ограничивающие многогранники.
Ребра многогранника – стороны граней многогранника.
Вершины многогранника – концы ребер многогранника (вершины граней многогранника).
Диагональ многогранника – отрезок, соединяющий две вершины, не принадлежащие одной грани.
Выпуклый многогранник – многогранник, расположенный по одну сторону от плоскости его любой грани.
Невыпуклый многогранник – многогранник, у которого найдется по крайней мере одна грань такая, что плоскость, проведенная через эту грань, делит данный многогранник на две или более частей.
Атанасян Л. С., В. Ф. Бутузов, С. Б. Кадомцев и др. Математика: алгебра и начала математического анализа, геометрия. Геометрия. 10–11 классы: учеб. Для общеобразоват. организаций: базовый и углубл. уровния. – М.: Просвещение, 2014. – 255 с. (стр. 58, стр. 60 – 61)
Долбилин Н. П. Жемчужины теории многогранников М. : – МЦНМО, 2000. – 40 с.: ил. (стр. 27 – 31)
Открытые электронные ресурсы:
Долбилин Н. П. Три теоремы о выпуклых многогранниках. Журнал Квант.
Теоретический материал для самостоятельного изучения
К определению понятия многогранника существует два подхода. Проведем аналогию с понятием многоугольника. Напомним, что в планиметрии под многоугольником мы понимали замкнутую линию без самопересечений, составленную из отрезков (рис. 1а). Также многоугольник можно рассматривать как часть плоскости, ограниченную этой линией, включая ее саму (рис. 1б). При изучении тел в пространстве мы будем пользоваться вторым толкованием понятия многоугольник. Так, любой многоугольник в пространстве есть плоская поверхность.
Б)
Рисунок 1 – разные подходы к определению многоугольника
Вторая трактовка понятия определяет многогранник как геометрическое тело, ограниченное конечным числом плоских многоугольников.
В дальнейшем, мы будем использовать вторую трактовку понятия многогранника.
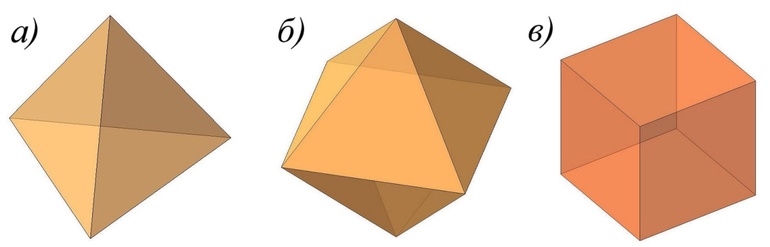
Уже известные вам тетраэдр и параллелепипед являются многогранниками. Потому что они являются геометрическими телами, ограниченные конечным числом плоских многоугольников. Еще один пример многогранника — октаэдр (рис. 2)
Рисунок 2 – изображение октаэдра
Многоугольники, ограничивающие многогранник, называются его гранями. Так, у тетраэдра и октаэдра гранями являются треугольники. У тетраэдра 4 грани, отсюда и его название от греч. τετρά-εδρον — четырёхгранник. У октаэдра 8 граней, а от греческого οκτάεδρον от οκτώ «восемь» + έδρα «основание».
Стороны граней называются ребрами, а концы ребер — вершинами многогранника. Отрезок, соединяющий две вершины, не принадлежащие одной грани, называется диагональю многогранника.
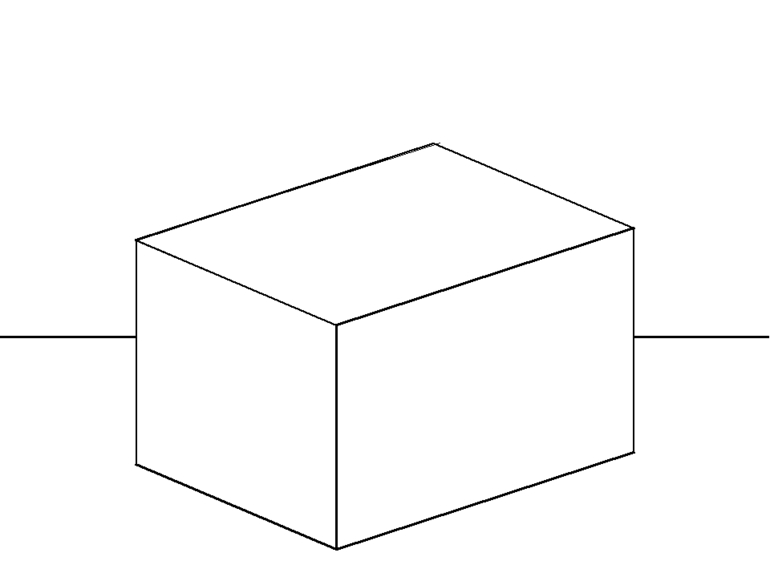
Многогранник называется выпуклым, если он расположен по одну сторону от плоскости каждой его грани. В остальных случаях многогранник называется невыпуклым (рис.3).
Рисунок 3 – Виды многогранников
Сумма плоских углов при вершине выпуклого многогранника
Рисунок 4 – сумма плоских углов пи вершине многогранника
Теорема Эйлера. Пусть В — число вершин выпуклого многогранника, Р — число его ребер, а Г — число его граней. Тогда верно равенство В – Р+Г= 2.
Теорема Эйлера играет огромную роль в математике. С ее помощью было доказано огромное количество теорем. Находясь в центре постоянного внимания со стороны математиков, теорема Эйлера получила далеко идущие обобщения. Более того, эта теорема открыла новую главу в математике, которая называется топологией.
Примеры и разбор решения заданий тренировочного модуля
Задание 1. Какие из перечисленных объектов НЕ могут быть элементами многогранника? Укажите номера в порядке возрастания.
Элементы многогранника, которые мы выделили: ребра, грани, вершины и диагонали. Ребро и диагональ многогранника – это отрезок. Грань многогранника – многоугольник, или иначе ограниченная часть плоскости. Вершины представляют собой точки. Таким образом, элементами многогранника не могут быть плоскость, луч, многогранник, прямая.
Задание 2. Сопоставьте геометрическим фигурам их вид
Б) пространственная фигура
Вспомним, что изобразить пространственную фигуру можно разными способами. Например, с помощью теней или изображением невидимых линий пунктиром. Так, среди всех изображений плоской фигурой является фигура под номером 1.
Многогранник – геометрическое тело, ограниченное конечным числом плоских многоугольников. Только на изображении 2 фигура ограничена многоугольниками. Таким образом, получаем следующий ответ: 1-А, 2-В, 3-Б
Многогранник
В трёхмерном пространстве, совокупность конечного числа плоских многоугольников, такая, что каждая сторона любого из многоугольников есть одновременно сторона другого (но только одного), называемого смежным с первым (по этой стороне); от любого из многоугольников, составляющих М., можно дойти до любого из них, переходя к смежному с ним, а от этого, в свою очередь, — к смежному с ним, и т. д. Эти многоугольники называются гранями, их стороны — рёбрами, а их вершины — вершинами М.
Приведённое определение М. получает различный смысл в зависимости от того, как определить Многоугольник. Если под многоугольником понимают плоские замкнутые ломаные (хотя бы и самопересекающиеся), то приходят к первому определению М. (вопросы, связанные с определяемыми таким образом М., будут рассмотрены в конце статьи). Основная часть статьи построена на основе второго определения М., при котором его грани являются многоугольниками, понимаемыми как части плоскости, ограниченные ломаными. С этой точки зрения М. есть поверхность, составленная из многоугольных кусков. Если эта поверхность сама себя не пересекает, то она есть полная поверхность некоторого геометрического тела, которое также называется М.; отсюда возникает третья точка зрения на М. как на геометрические тела, причём допускается также существование у этих тел «дырок», т. е. — что эти тела не односвязаны.
М. называется выпуклым, если он весь лежит по одну сторону от плоскости любой его грани; тогда грани его тоже выпуклы. Выпуклый М. разрезает пространство на две части — внешнюю и внутреннюю. Внутренняя его часть есть выпуклое тело. Обратно, если поверхность выпуклого тела многогранная, то соответствующий М. — выпуклый.
Важнейшие теоремы общей теории выпуклых М. (рассматриваемых как по верхности) следующие.
Теорема Эйлера (1758): число вершин минус число рёбер плюс число граней выпуклого М. — эйлерова характеристика М. — равно двум; символически: в — р + г = 2.
Теорема Коши (1812) (в современной форме): если два выпуклых М. изометричны друг другу (т. е. один М. может быть взаимно однозначно отображён на другой М. с сохранением длин лежащих на нём линий), то второй М. может быть получен из первого движением его как жёсткого целого (или движением и зеркальным отражением). Отсюда, в частности, следует, что если грани выпуклого М. жестки, то он сам жёсток, хотя бы его грани были скреплены друг с другом по ребрам шарнирно. Это предполагал верным ещё Евклид и знает всякий, клеивший картонные модели М., но доказал Коши только через 2000 лет после Евклида.
Теорема А. Д. Александрова (1939): если взять конечное число плоских выпуклых многоугольников (сделанных, например, из бумаги) и указать, какую сторону какого из них с какой стороной какого другого мы будем склеивать (склеиваемые стороны, конечно, должны быть одинаковой длины), т. е. если рассмотреть развёртку (выкройку) М., то для того, чтобы так склеенную замкнутую поверхность можно было, соответственно расправив (т. е. изогнув, если нужно, но не растягивая, не сжимая, не разрывая и больше не склеивая), превратить в поверхность выпуклого М., необходимо и достаточно, чтобы: а) удовлетворялось условие Эйлера в — р + г = 2 и б) чтобы сумма плоских углов, сходящихся при склеивании в одной вершине, для любой вершины была меньше 360°. Эта теорема есть теорема существования, т. е. она показывает, с какими развёртками существуют выпуклые М., а теорема Коши есть для неё теорема единственности, т. е. она показывает, что существует только один (с точностью до движения и отражения) выпуклый М. с такой развёрткой.
Теорема (существования) Минковского (1896): существует выпуклый М. с любыми площадями граней и любыми направлениями внешних нормалей к ним, лишь бы сумма векторов, имеющих направления нормалей и длины, равные площадям соответствующих граней, была равна нулю и эти векторы не лежали бы все в одной плоскости. Эти условия необходимы.
Теорема (единственности) Минковского (1896): выпуклый М. вполне определяется площадями своих граней и направлениями внешних нормалей к ним; и углубляющая её теорема (единственности) А. Д. Александрова: два выпуклых М. с попарно параллельными гранями не равны друг другу только в том случае, если для одной из пар параллельных граней с одинаково направленными внешними нормалями одна из этих граней может быть при помощи параллельного переноса вложена в другую.
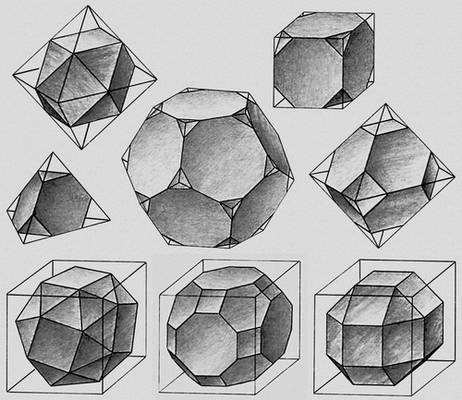
Наиболее важны следующие специальные выпуклые М.
Куб и октаэдр дуальны, т. е. получаются друг из друга, если центры тяжести граней одного принять за вершины другого или обратно. Аналогично дуальны додекаэдр и икосаэдр. Тетраэдр дуален сам себе. Правильный додекаэдр получается из куба построением «крыш» на его гранях (способ Евклида), вершинами тетраэдра являются любые четыре вершины куба, попарно не смежные по ребру. Так получаются из куба все остальные правильные М.
В приведённой ниже таблице указаны радиус описанной сферы, радиус вписанной сферы и объём всех правильных М. (а — длина ребра М.).
Изоэдры и изогоны. Изоэдром (изогоном) называется такой выпуклый М., что группа его поворотов (первого и второго, т. е. с отражениями, родов) вокруг центра тяжести переводит любую его грань (вершину) в любую другую его грань (вершину). Каждому изоэдру (изогону) соответствует дуальный изогон (изоэдр). Если М. одновременно и изогон и изоэдр, то он правильный М. Комбинаторно различных изоэдров (изогонов) имеется 13 специальных типов и две бесконечные серии (призмы и антипризмы). Оказывается, что каждый из этих изоэдров может быть реализован так, что все его грани суть правильные многоугольники. Полученные так М. называются полуправильными многогранниками (телами Архимеда).
| Радиус описанной сферы | Радиус вписанной сферы | Объём |
|---|---|---|
Тетраэдр 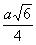 | 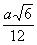 | 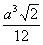 |
Куб 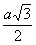 | 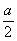 | 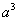 |
Октаэдр 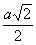 | 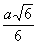 | 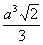 |
Додекаэдр 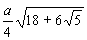 | 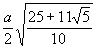 | 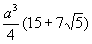 |
Икосаэдр 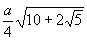 | 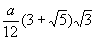 | 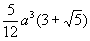 |
Параллелоэдры (выпуклые; найдены рус. учёным Е. С. Федоровым в 1881) — М., рассматриваемые как тела, параллельным перенесением которых можно заполнить всё бесконечное пространство так, чтобы они не входили друг в друга и не оставляли пустот между собой, т. е. образовать разбиение пространства. Таковы, например, куб или правильная 6-угольная призма. Топологически различных сеток рёбер параллелоэдров пять. Число их граней — 6, 8, 12, 12, 14. Для того чтобы М. был параллелоэдром, необходимо и достаточно, чтобы он был выпуклым М. одного из пяти указанных топологических типов и чтобы все грани его имели центры симметрии.
Если параллелоэдры разбиения смежны целыми гранями, разбиение называется нормальным. Центры параллелоэдров такого разбиения образуют решётку, т. е. совокупность всех точек с целыми координатами относительно какой-то, вообще говоря, не прямоугольной декартовой системы координат. Множество точек пространства, из которых каждая отстоит от некоторой данной точки О рассматриваемой решётки Λ не дальше, чем от всякой другой точки этой решётки, называется областью Дирихле (или областью Вороного) DoΛ точки О в решётке Λ. Область DoΛ является выпуклым М. с центром в точке О. Совокупность областей Дирихле всех точек произвольной решётки образует нормальное разбиение пространства. Существует замечательная теорема: произвольное (даже n-мерное) нормальное разбиение на параллелоэдры, в каждой из вершин которого сходится n + 1 параллелоэдр, может быть аффинным преобразованием превращено в разбиение Дирихле для некоторой решётки.
Всякое движение, переводящее в себя решётку Λ и оставляющее на месте её точку О, преобразует в себя область DoΛ и обратно. Группу всех таких движений называют голоэдрией решётки. Их всего семь: кубическая, ромбоэдрическая, квадратная (или тетрагональная), ортогональная (или ромбическая), моноклинная, триклинная и гексагональная.
Кристаллографические многогранники. Каждая из семи рассмотренных групп имеет подгруппы, всех различных таких групп и их подгрупп 32; их называют кристаллографическими классами. Пусть какой-нибудь кристаллографический класс есть подгруппа некоторой голоэдрии, тогда говорят, что он принадлежит этой голоэдрии (или входит в состав её сингонии), если этот класс не является подгруппой никакой голоэдрии, содержащейся в данной. Если взять плоскость, не проходящую через точку О, и подвергнуть её всем поворотам какого-нибудь кристаллографического класса, то полученные плоскости ограничивают либо некоторый изоэдр с центром в точке, либо бесконечное выпуклое призматическое тело, либо многогранный угол. Полученные тела называются простыми формами кристаллов, в первом случае замкнутыми, во втором и третьем — открытыми. Две простые формы считают одинаковыми, если они имеют один и тот же комбинаторный тип, порождены одним и тем же кристаллографическим классом и повороты этого класса одинаковым образом связаны с формой. Существует 30 различных в этом смысле замкнутых форм и 17 открытых, каждая из них имеет вполне определённое название (см. Кристаллы).
Основываясь на первом (указанном в начале статьи) определении М., можно указать ещё четыре правильных невыпуклых многогранника (т. н. тела Пуансо), впервые найденных французским математиком Л. Пуансо в 1809. Доказательство несуществования других невыпуклых правильных М. дал французский математик О. Коши в 1811. В этих М. либо грани пересекают друг друга, либо сами грани — самопересекающиеся многоугольники. Для изучения вопросов, связанных с площадями поверхностей и объёмами таких М., удобно пользоваться именно первым определением М.
Если у М. можно так ориентировать грани, чтобы каждое ребро в тех двух гранях, которые смежны по этому ребру, имело бы обратные направления, то его называют ориентируемым, в противном случае — неориентируемым. Для ориентируемого М. (даже если он самопересекающийся и его грани — самопересекающиеся многоугольники) можно ввести понятия площади поверхности и величины объёма. Площадью ориентируемого М. называют просто сумму площадей его граней (об определении площади самопересекающегося многоугольника см. Многоугольник). Для определения объёма надо заметить, что совокупность внутренних кусков граней М. разрезает пространство на определённое число связных кусков, из которых один по отношению к М. бесконечный (внешний), а остальные конечные (внутренние). Если из внешней по отношению к М. точки провести отрезок в какую-либо внутреннюю точку внутреннего куска, то сумму «коэффициентов» тех внутренних кусков граней М., которые пересечёт этот отрезок, называют коэффициентом рассматриваемого внутреннего куска М. (она не зависит от выбора внешней точки О); такой коэффициент есть целое положительное, отрицательное число или нуль. Сумму обычных объёмов всех внутренних кусков М., умноженных на эти их коэффициенты, называют объёмом М.
Можно рассматривать и n-мерные М. Некоторые из указанных определений и теорем имеют n-мерное обобщение. В частности, найдены все выпуклые правильные М.; при n = 4 их оказалось 6, а при всех больших n всего три: обобщение тетраэдра, куба и октаэдра. В то же время, например, неизвестны все четырёхмерные изоэдры и изогоны.
Примеры нерешенных задач теории многогранников.
1) Немецкий математик Э. Штейниц дал примеры того, что не для всякого топологического типа сетки рёбер выпуклого М. существует М., который можно описать вокруг шара; в общем виде задача не решена.
2) Параллелоэдры суть выпуклые основные области групп параллельных переносов, но до сих пор не определены основные типы стереоэдров, т. е. выпуклых основных областей произвольных (федоровских) дискретных групп движений. 3) Определение всех типов четырёхмерных изоэдров.
Лит.: Фёдоров Е. С., Начала учения о фигурах, СПБ, 1885; Александров А. Д., Выпуклые многогранники, М. — Л., 1950; Вороной Г. Ф., Собр. соч., т. 2, К., 1952; Brückner М., Vielecke und Vielflache. Theorie und Geschichte, Lpz., 1900; Steinitz E., Vorlesungen liber die Theorie der Polyeder unter Einschiuss der Elemente der Topologie. B., 1934; Coxeter H. S. М., Regular polytopes, 2 ed., L. — N. Y., 1963.
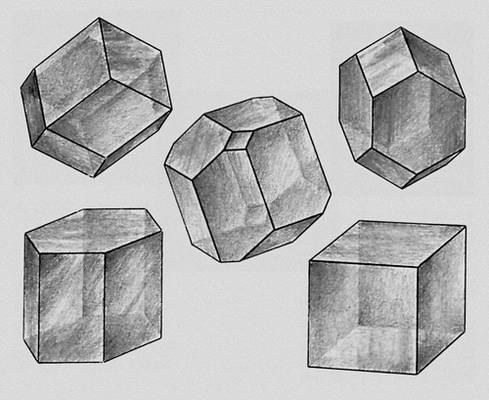
Выпуклые параллелоэдры (тела Фёдорова).
Правильные невыпуклые многогранники (тела Пуансо).
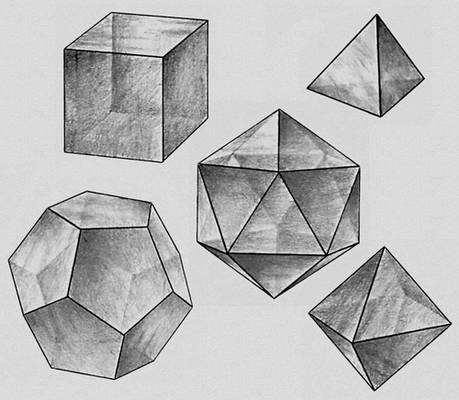
Правильные выпуклые многогранники (тела Платона).
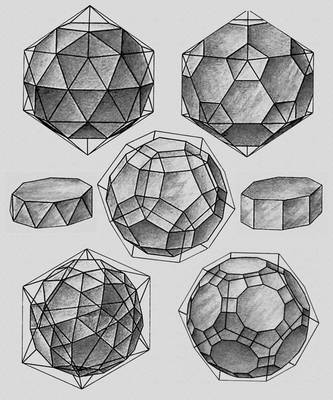
Полуправильные многогранники (тела Архимеда).
Полуправильные многогранники (тела Архимеда).