Что такое метод площадей
Что такое метод площадей
§2. Площадь треугольника. Метод площадей
В школьном курсе геометрии доказано несколько формул площади треугольника. Напомним их.
При вычислении площади из этих формул следует выбрать ту, которая в условиях конкретной задачи приводит к более простому решению.
Для примера, рассмотрим два треугольника:
`DeltaABC:` `AB=13`, `BC=14`, `AC=15`;
`DeltaKML:` `KL=sqrt(13)`, `LM=sqrt(14)`, `KM=sqrt(15)`;
Надо найти площадь и радиус описанной окружности.
Для треугольника `ABC` удобен ход решения такой:
`p=1/2(AB+BC+AC)=21`, по формуле Герона
`S_(ABC)=sqrt(21*6*7*8)= ul(84)` и по формуле (5)
тогда `sinM=sqrt(1-64/(210))=(sqrt(146))/(sqrt(14)*sqrt(15))` и по формуле (2):
тогда `R=(KL)/(2sinM)=ul((sqrt(13)*sqrt(14)*sqrt(15))/(2*sqrt(146)))=(sqrt(13)*sqrt7*sqrt(15))/(2*sqrt(73))` (точно также по формуле 5).
Сравнение площадей треугольников обычно опирается на одно из следующих утверждений:
$$ 2.<1>^<○>$$. Площади треугольников с одинаковой высотой относятся как длины соответствующих оснований. В частности, если точка `D` лежит на основании `AC` (рис. 6а), то
$$ 2.<2>^<○>$$. Площади треугольников с общим углом относятся как произведения сторон, заключающих этот угол (см. рис. 6б):
$$ 2.<3>^<○>$$. Площади подобных треугольников относятся как квадраты их
сходственных сторон, т. е. если `Delta ABC
DeltaA_1B_1C_1`, то `(S_(A_1B_1C_1))/(S_(ABC))=((A_1B_1)/(AB))^2`.
Все эти утверждения легко доказываются с использованием соответственно формул площади (1) и (2).
Обратим внимание на важное свойство медиан треугольника.
Три медианы треугольника разбивают его на `6` треугольников с общей вершиной и равными площадями.
Докажем, например, для треугольника `BOM`, что `S_(BOM)=1/6S_(ABC)`.
Дан треугольник `ABC`. Точка `D` лежит на стороне `AB`, `AD:DB=1:2`, точка `K` лежит на стороне `BC`, `BK:KC=3:2` (рис. 8а). Отрезки `AK` и `CD` пересекаются в точке `O`. Найти отношение площади четырёхугольника `DBKO` к площади треугольника `ABC`.
2. Через точку `D` проведём прямую `DL«|\|«AK`. По теореме о пересечении сторон угла параллельными прямыми (`/_ABC`, `DL«|\|«AK`) имеем `(BL)/(LK)=(BD)/(AD)`, откуда `LK=y`.
По той же теореме (`/_DCB`, `OK«|\|«DL`) получим `(DO)/(DC)=(LK)/(LC)`, `DO=1/3DC`.
3. Теперь находим `S_(ADO):S_(ADC)=DO:DC`, `a=1/3(1/3S)=1/9S`.
(Можно по теореме Менелая для треугольника `BCD` и секущей `CD:`
`(BK)/(KC)*(CO)/(OD)*(DA)/(AB)=1 iff 3/2*(CO)/(OD)*1/3=1 iff CO=2OD=>OD=1/3DC`).
Находим площадь: `sigma=3/5S-a=(3/5-1/9)S=22/45S`.
Найти площадь треугольника, две стороны которого равны `3` и `7`, а медиана к третьей стороне равна `4` (рис. 9).
Пусть `AB=3`, `BC=7`, `AM=MC` и `BM=4`. Достроим треугольник `ABC` до параллелограмма, для этого на прямой `BM` отложим отрезок `MD=BM` и соединим точки: `A` с `D` и `C` с `D`. Противоположные стороны параллелограмма равны: `(DC=AB)` и равны площади треугольников `ABC` и `DBC` (общее основание `BC` и равные высоты из вершин `A` и `D`).
В треугольнике `DBC` известны все три стороны: `BC=7`, `DC=3`, `BD=2BM=8`.
Находим его площадь по формуле Герона: `p=9`, `S_(BCD)=6sqrt3`.
Значит и `S_(ABC)=6sqrt3`.
В решении этой задачи дополнительным построением получен треугольник, площадь которого равна площади заданного и легко вычисляется по данным задачи. Приведём ещё одну задачу, где сначала вычисляется площадь дополнительно построенной фигуры, а затем легко находится искомая площадь.
Найти площадь треугольника, если его медианы равны `3`, `4` и `5`.
По свойству медиан `AO=2/3m_a`, `CO=2/3m_c` и `ON=1/3m_b`. В треугольнике `AOC` известны две стороны `AO` и `CO` и медиана третьей стороны `ON`. Площадь этого треугольника найдём как в предыдущей задаче.
Достроим треугольник `AOC` до параллелограмма `AOCD`, `S_(AOC)=S_(DOC)`, в треугольнике `DOC` известны три стороны:
`DO=2ON=2/3m_b`, `OC=2/3m_c`, `DC=AO=2/3m_a`.
Площадь треугольника `DOC` вычисляем по формуле Герона `S_1=S_(AOC)=S_(DOC)=8/3`. Сравним теперь площадь треугольника `ABC` (обозначим её `S`) с площадью треугольника `AOC`. Из теоремы 2 о медианах и площадях следует `S_(AOC)=S_(AON)+S_(NOC)=2*1/6S=1/3S`.
В следующей задаче докажем лемму об отношении площади треугольника к площади другого треугольника, построенного из медиан первого.
Найти отношение площади `S` треугольника к площади `S_0` треугольника, составленного из медиан первого.
Рассмотрим рис. 10. В построенном треугольнике `OCD` стороны таковы: `OC=2/3m_c`, `OD=2/3m_b`, `CD=2/3m_a`. Очевидно, что треугольник со сторонами `m_a`, `m_b`, `m_c` подобен (по третьему признаку) треугольнику со сторонами `2/3m_a`, `2/3m_b`, `2/3m_c`.
| `S_(m_am_bm_c)=3/4S_(abc)`. |
Около окружности радиуса `sqrt3` описан треугольник. Найти его площадь, если одна из его сторон точкой касания делится на отрезки `9` и `5`.
Пусть `AP=9`, `PC=5` (рис. 11) и пусть `BM=x`. По свойству касательных `AM=AP`, `CN=CP` и `BN=BM`, поэтому стороны треугольника таковы: `AC=14`, `AB=9+x`, `BC=5+x`, тогда `p=14+x`. (Заметим, что `p=AC+BM`!). По формулам площади (3) и (4) имеем: `S=pr=(14+x)sqrt3` и `S=sqrt((14+x)x*5*9)`. Приравниваем правые части, возводим в квадрат, приводим подобные члены, получаем `x=1`. Вычисляем площадь треугольника:
Приём, применённый в решении этой задачи, когда площадь фигуры выражается двумя различными способами, часто используется в задачах на доказательство.
Проведём два примера, в каждом выведем полезную формулу.
В треугольнике `ABC` угол `C` равен `varphi`, `AC=b`, `BC=a` (рис. 12). Доказать, что биссектриса `CD` равна `(2ab)/(a+b) cos varphi/2`.
Обозначим `CD=x`. Очевидно, что `S_(ABC)=S_(ACD)+S_(DCB)`. По формуле (2) `S_(ABC)=1/2 ab sin varphi`, `S_(ACD)=1/2 bx sin varphi/2`, `S_(BDC)=1/2 ax sin varphi/2`. Таким образом, имеем: `1/2 ab sin varphi=1/2(a+b)x sin varphi/2`. Используем формулу синуса двойного угла `sin varphi=2sin varphi/2 cos varphi/2`, получим:
называется окружность, касающаяся одной из сторон треугольника и продолжений двух других сторон. Таких окружностей, очевидно, три (рис. 13). Их радиусы обычно обозначаются `r_a`, `r_b`, `r_c` в зависимости от того, какой стороны окружность касается.
Вневписанная окружность касается стороны `a=BC` треугольника `ABC` (рис. 14). Доказать, что `S_(ABC)=r_a(p-a)`, где `2p=a+b+c`.
Считаем площадь `S_0` четырёхугольника `ABI_aC`:
`S_0=S_(ABC)+S_(BCI_a)` и `S_0=S_(ABI_a)+S_(ACI_a)`, откуда
Метод площадей для решения задач
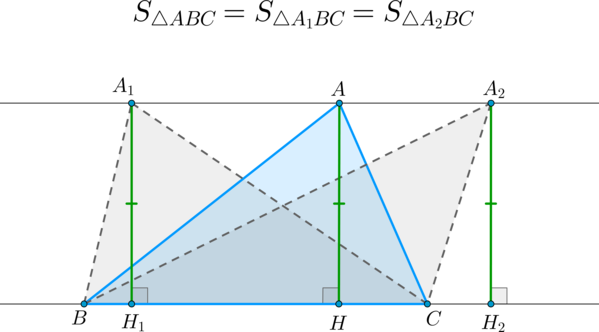
\(\blacktriangleright\) Теорема 1. Если вершину треугольника перемещать по прямой, параллельной противолежащей стороне, то площадь при этом останется прежней.
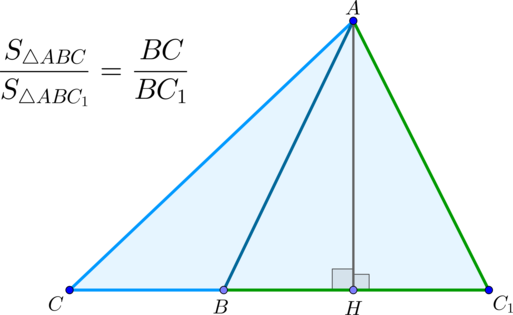
\(\blacktriangleright\) Теорема 2. Если два треугольника имеют равные высоты (общую высоту), то их площади относятся как основания, к которым эти высоты проведены.
\(\blacktriangleright\) Теорема 3. Если два треугольника имеют одинаковые стороны (общую сторону), то их площади относятся как высоты, которые к этим сторонам проведены.
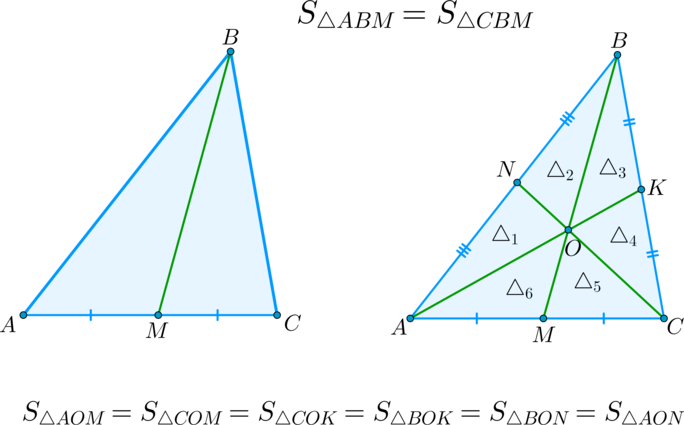
\(\blacktriangleright\) Следствие: Медиана треугольника делит его на два треугольника, равных по площади.
\(\blacktriangleright\) Следствие: Все три медианы треугольника делят его на шесть треугольников, равных по площади.
\(\blacktriangleright\) Теорема 4. Если два треугольника имеют по равному углу (общему углу), то их площади относятся как произведения сторон, образующих эти углы.
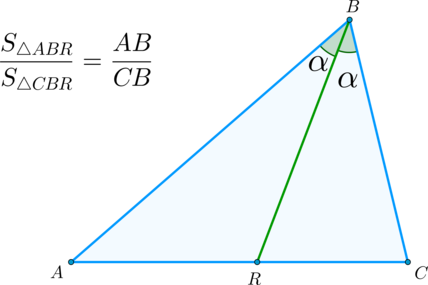
\(\blacktriangleright\) Следствие: Биссектриса угла треугольника делит его на два треугольника, площади которых относятся как стороны, образующие этот угол.
\(\blacktriangleright\) Теорема 5. Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Доказательство: т.к. треугольники подобны, то все стороны одного треугольника в \(k\) раз больше всех сторон другого, а углы между сходственными сторонами равны. Значит, \[\dfrac
\(\blacktriangleright\) Следствие: Все три средние линии треугольника делят его на четыре равных треугольника, и, как следствие, равных по площади.
Задачи на применение методов измерения площадей в ЕГЭ по математике встречаются ежегодно, поэтому при подготовке к прохождению аттестационного испытания учащимся непременно стоит повторить теорию по данной теме. Уметь справляться с такими заданиями обязательно должны выпускники, сдающие как базовый, так и профильный уровень экзамена. Разобравшись с основной теорией и практическими упражнениями на вычисление площадей плоских фигур, старшеклассники смогут решать задачи с любым количеством действий и рассчитывать на получение достойных баллов по итогам сдачи ЕГЭ.
Как подготовиться к экзамену?
Зачастую найти источник, в котором представлен весь базовый теоретический материал, оказывается не так легко, как может показаться на первый взгляд. В нужный момент школьного учебника может просто не быть под рукой. А найти необходимые формулы иногда оказывается достаточно сложно даже в Интернете.
Образовательный портал «Школково» поможет вам подготовиться к сдаче аттестационного испытания. Все основы теории по теме «Измерение площадей плоских фигур» систематизированы и изложены нашими специалистами с учетом их богатого опыта в максимально доступной форме. Ознакомившись с представленной информацией, выпускники смогут восполнить пробелы в знаниях.
Чтобы качественно подготовиться к ЕГЭ, школьникам из Москвы и других городов необходимо не только повторить теорию по теме «Вычисление площадей плоских фигур», но и попрактиковаться в выполнении соответствующих упражнений. Найти задачи вы можете в разделе «Каталог». Для каждого задания наши специалисты прописали подробный алгоритм решения и указали правильный ответ. Последовательно выполняя простые и более сложные упражнения по данной теме, учащиеся смогут отработать навык решения подобных задач. Перечень заданий в соответствующем разделе постоянно дополняется и обновляется.
Ознакомиться с теорией и попрактиковаться в решении задач на вычисление площади треугольника и других фигур, подобных тем, которые включены в ЕГЭ, можно в режиме онлайн. При необходимости любое упражнение можно сохранить в «Избранное». Еще раз повторив базовую теорию, выпускник может в дальнейшем вернуться к задаче на вычисление площади фигуры с целью обсуждения алгоритма ее решения со своим преподавателем.
Решении задач по геометрии при подготовке к ГИА
Научно-практическая конференция учащихся и педагогов Татищевского муниципального района 2013г.
МОУ « Средняя общеобразовательная школа №1 р. п. Татищево»
Решении задач по геометрии при подготовке к ГИА.
,
учитель математики
МОУ « СОШ №1 р. п. Татищево»
первой квалификационной категории
ТАТИЩЕВО 2013
Оглавление
Подготовка к государственной итоговой аттестации (ГИА) – неотъемлемая часть современного курса математики. Задачи по геометрии занимают примерно третью часть всех заданий КИМов. Геометрия является очень мощным средством развития личности в самом широком диапазоне. Среди дисциплин математического цикла геометрия выделяется своим вольнодумством, неким особым свободолюбивым характером, нежелающим подчиняться стандартам, нормам, алгоритмам.
Целью изучения геометрии, конечно, является знание. Но нужно всегда помнить, что геометрия есть феномен общечеловеческой культуры. Человек не может развиваться культурно и духовно, если он не изучал в школе геометрию. Геометрия возникла не только из практических, но и из духовных потребностей человека.
Научной и нравственной основой курса геометрии является принцип доказательности всех утверждений. И это единственный школьный предмет, включая даже предметы математического цикла, полностью основанный на последовательном выводе всех утверждений.
Геометрия, впрочем, как и алгебра, является носителем собственного познания мира. Овладение этим методом – важнейшая цель образования. Процесс изучения геометрии должен включать самые разнообразные виды деятельности. В том числе и даже в первую очередь – решение задач. Задача – это не только умения, это и элемент знания. Ученик должен ознакомиться с определенным набором достаточно трудных геометрических задач, научиться решать задачи, следуя известным образцам. В геометрии в отличие от алгебры алгоритмов очень мало, почти нет. Поэтому при обучении возрастает значение опорных задач, обобщающих полезный факт, либо иллюстрирующий метод или прием.
Метод площадей
Основные свойства площадей
В элементарной математике, самыми трудными считаются геометрические задачи. Как научиться решать геометрические задачи, особенно сложные, конкурсные? При решении геометрических задач, как правило, алгоритмов нет, и выбирать наиболее подходящую к данному случаю теорему не просто. Поэтому, желательно в каждой теме выработать какие-то общие положения, которые полезно знать всякому решающему геометрические задачи.
Предлагаем один из алгоритмов решения многих геометрических задач – метод площадей, т. е. решение задач с использованием свойств площадей
Если вершину треугольника передвигать по прямой, параллельной основанию, то площадь при этом не изменится
Если два треугольника имеют одинаковые высоты, то отношение их площадей равно отношению длин оснований (сторон, на которые опущены эти высоты).
Если два треугольника имеют общий угол, то их площади относятся как произведение сторон, заключающих этот угол.
Отношение площадей подобных треугольников равны квадрату коэффициента подобия.
Медиана треугольника делит его на две равновеликие части.
Медианы треугольника делят его на три равновеликие части
Средние линии треугольника площади S отсекают от него треугольники площади, которых равны одной четвертой части площади ▲ABC
Медианы треугольника делят его на 6 равновеликих частей.
Система математических задач, решаемых методом площадей
В современных учебниках, пособиях и различного рода задачниках, к сожалению, уделяется мало внимания психологическим факторам, влияющим на успешность обучения математике. А именно, воспитание у учащихся уверенности в своих силах, развитие умения пользоваться прошлым опытом.
Берутся два общеизвестных утверждения, которые являются базовыми. На основе этих утверждений выстраиваются две «цепочки» задач по нарастающему уровню сложности. Решения задач в этих «цепочках» основаны на базовых утверждениях и на решении предыдущих задач.
Утверждение 1. Два треугольника являются равновеликими, если равны их высоты и основания.
Задача 1. Докажите, что диагональ параллелограмма делит его на два равновеликих треугольника.
Решение. Высоты треугольников ABD и BCD равны. AD = BC (по свойству параллелограмма). Тогда в силу утверждения 1 S▲ABD = S▲BCD
Решение. Проведем отрезок КЕ. Тогда в силу задачи 2 S▲KME = S▲KMB + S▲MEC, а S▲KNE = S▲AKN + S▲EDN
Отсюда S▲KMEN = S▲KMB + S▲MEC + S▲KNE + S▲EDN
Введем следующие обозначения:
Задача 5. Каждая диагональ четырехугольника делит его на треугольники одинаковой площади. Докажите, что это параллелограмм.
Утверждение 2. Медиана треугольника делит его на два равновеликих треугольника.
Решение. Проведем диагональ ВD. Тогда, исходя из утверждения 2, получим, что SABCD = 2 S .
Решение. Проведя диагональ ВD и рассуждая аналогично задаче 6, получим, что SABCD = 2SEBFD
Задача 9. Докажите, что диагонали параллелограмма делят его на четыре равновеликих треугольника.
Решение. В силу задачи 1 и утверждения 2 будем иметь
S▲AOB = S▲BOC = S▲COD =S▲DOA
Задача 10. Середины двух параллельных сторон параллелограмма соединены с противолежащими вершинами. Какая часть площади параллелограмма ограничена проведенными отрезками?
Решение. Проведем отрезок МК. Тогда в силу задачи 9 SMFKE = 1/4SABCD.
Задача 11. Дан выпуклый четырехугольник ABCD. Середины сторон АВ и CD обозначены соответственно через К и М, точку пересечения отрезков ВМ и СК – через Р, точку пересечения отрезков АМ и DК – через О. Докажите, SMOKP = S▲BPC + S▲AOD
Решение. Проведем диагональ ВD. Так как DК и ВМ медианы вновь полученных треугольников, то SAKD=1/2SABD, SBMC=1/2SBCD. Отсюда S▲AKD + S▲BMC = 1/2 S АВС D (1) Проведя диагональ АС и учитывая, что АМ и СК медианы уже вновь полученных треугольников, получим SKBC=1/2SABC, SAMD=1/2SACD.
Тогда S▲KBC + S▲AMD = 1/2 SABCD (2).
В этой сумме дважды учтены площади треугольников ВРС и АОD, но не учтена площадь четырехугольника МОКР. Поэтому SMOKP = S▲BPC + S▲AOD.
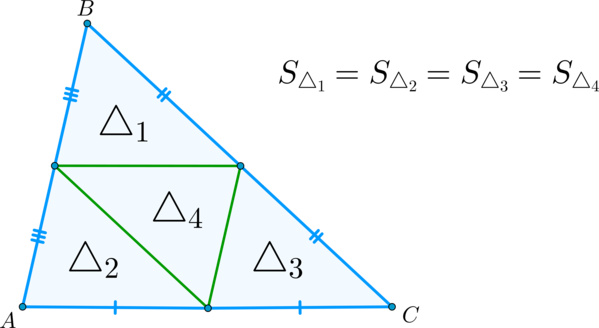
Решение. Медиана делит площадь треугольника пополам, поэтому площади треугольников ABC, BB1C и CC1B1 равны между собой. Площадь треугольника ACD равна площади треугольника ADD1, площадь треугольника ADD1 равна площади треугольника AA1D1 и т. д. Тогда S▲BB1C1 = 2S▲ABC, S▲CC1D1 = 2S▲BCD, S▲AA1B1 = 2S▲DBA, S▲DD1A1 = 2S▲CAD. Суммируя эти равенства, получим S▲BB1C1 + S▲CC1D1 + S▲AA1B1 + S▲DD1A1.Обозначим площадь четырехугольника АВСD через S, тогда площадь четырех построенных треугольников равна 4S, а площадь четырехугольника А1В1С1D1 равна 5S.
Задача 13. Вершина А квадрата АВСD соединена с точкой О – серединой ВС, вершина В – с точкой Е – серединой СD, вершина С – с точкой N – серединой АD, а вершина D – с точкой К – серединой АВ. Точки пересечения проведенных прямых L, M, R, и Р служат вершинами четырехугольника LMRP.
Докажите, что SLMRP=51SABCD.

Продолжим «цепочку» задач, исходной фигурой в которых будет выступать уже треугольник.
Задача 14. На продолжении стороны АВ треугольника АВС взята точка К так, что АВ = ВК. Точка L – середина ВС. Зная, что S▲BKL = S, найдите S▲ABC.
Решение. Произведя дополнительные построения, приняв во внимание обозначения на чертеже и опираясь на утверждение 2, видим, что решение следует непосредственно из чертежа.
Задача 16. На продолжении стороны треугольника АВС взята точка D так, что АС = СD. Пусть М – середина стороны АВ, а К – точка пересечения отрезков ВС и МD. Докажите, что площадь треугольника ВКD равна площади четырехугольника АМКС.
Опорные задачи, решаемые методом площадей
Метод площадей имеет много разновидностей. Его применяют, например, при замене отношения отрезков, расположенных на одной прямой, отношением площадей треугольников с общей вершиной, основаниями которых являются рассматриваемые отрезки.
При решении задач методом площадей часто применяют основные формулы, выражающие площадь треугольника.
Обозначим, через А, В и С величины соответствующих углов треугольника АВС, а через а, b и с, как обычно, длины противолежащих им сторон, 2р – периметр треугольника, r и R – соответственно радиус вписанной и описанной окружности.
В этих обозначениях для площади треугольника справедливы следующие формулы:





Формулы (1), (4) и (5) хорошо известны, формулы (2), (3) получаются из формулы (1), используя теорему синусов. Формула (4) справедлива для любого описанного многоугольника.
Используя формулу (1) для площади треугольника, можно доказать теорему о биссектрисе внутреннего угла треугольника.
Теорема. Если 







Используя формулу (2.1) имеем

Рассмотрим опорные задачи, решаемые методом площадей.
Пример 1. Пусть две прямые пересекаются в точке А. В и В1 – любые две точки на одной прямой, а С и С1 – на другой. Докажите, что 


Пример 2. На сторонах АВ и АС треугольника АВС взяты точки В1 и С1 так, что 


Решение следует непосредственно из предыдущего примера.
Пример 3. Докажите, что длину биссектрисы 











Рассмотрим еще одну полезную задачу.
Используя результаты предыдущих задач, рассмотрим еще один важный пример, который в учебнике «Геометрия. 7-9 классы» назван типичной задачей.

Решение. Пусть ВР и КМ пересекаются в точке О (рис. 14) и 











При решении задач методом площадей следует помнить, что
1) Диагонали трапеции делят ее на четыре треугольника. Треугольники, прилежащие к боковым сторонам, равновелики.
2) Диагонали выпуклого четырехугольника делят его на четыре треугольника. Произведение площадей треугольников прилегающих к противоположным сторонам равны.
Заключение
Решение задач методом площадей необходимо учащимся в наше время, как при подготовке к ГИА. Владение приемами решения задач методом площадей можно считать критерием знаний основных разделов школьной геометрии.
В данной работе показано, что тема «Метод площадей» обладает множеством разнообразных задач, направленных на повышение интереса к изучению геометрии, на развитие мышления школьников, на развитие нравственных качеств. Метод площадей это использование формул и свойств площадей при решении задач, в которых может не упоминаться о площадях.
Подобранные задачи и методические рекомендации могут быть использованы учителями математики в их практической деятельности, при организации внеклассной работы, при подготовке к ГИА, что позволяет повысить эффективность обучения геометрии.
Именно такие задачи играют большую роль в формировании логического мышления и математической культуры у школьников, Поэтому учащиеся, владеющие данным методом решения задач, успешно справляются с другими задачами.
Литература
6) Барчунова познавательного интереса к геометрии у учащихся 6-7 классов// «Математика в школе», 1974. №6.