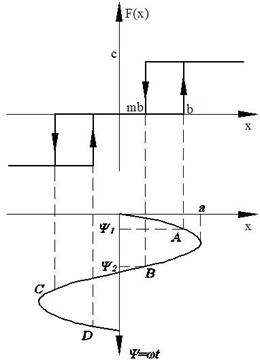
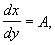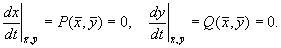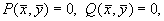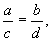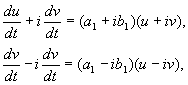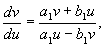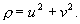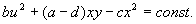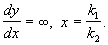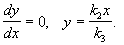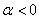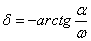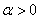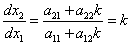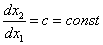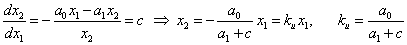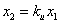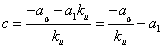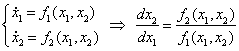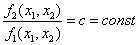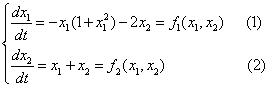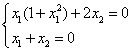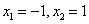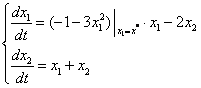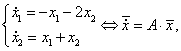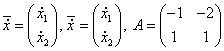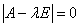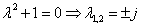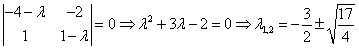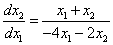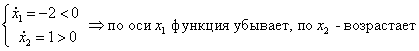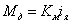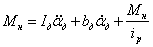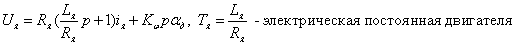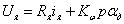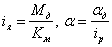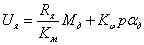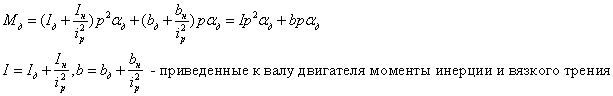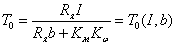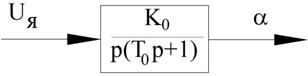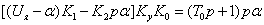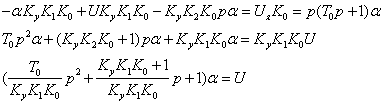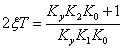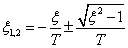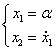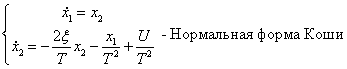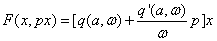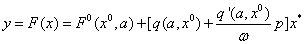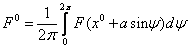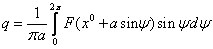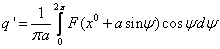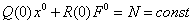Что такое метод изоклин в фазовом пространстве нелинейной системы

Метод изоклин для дифференциальных уравнений 1-го порядка

Дифференциальное уравнение первого порядка

Если в каждой точке области задано значение некоторой величины, то говорят, что в области задано поле этой величины. Таким образом, дифференциальное уравнение (1) определяет поле направлений.

Задача интегрирования дифференциального уравнения (1) может быть теперь истолкована так: найти такую кривую, чтобы касательная к ней в каждой точке имела направление, совпадающее с направлением поля в этой точке.

где — параметр. Придавая параметру близкие числовые значения, получаем достаточно густую сеть изоклин, с помощью которых можно приближенно построить интегральные кривые дифференциального yравнения (1).

Замечание 1. Нулевая изоклина дает уравнение линий, на которых могут находиться точки максимума и минимума интегральных кривых.

Для большей точности построения интегральных кривых находят также геометрическое место точек перегиба. Для этого находят в силу уравнения (1):

и приравнивают ее нулю. Линия, определяемая уравнением

и есть возможное геометрическое место точек перегиба.

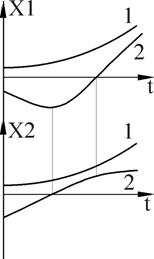
Проведенное исследование позволяет нам приближенно построить семейство интегральных кривых уравнения (рис.6).

Интегральные кривые в точках пересечения с этими изоклинами имеют горизонтальные касательные.

Определим, имеют ли интегральные кривые на изоклинах экстремум. Для этого найдем вторую производную:

Для исследования направления вогнутости интегральных кривых найдем вторую производную:

Правая часть исходного уравнения во всех точках плоскости удовлетворяет условиям теоремы существования и единственности, поэтому через каждую точку плоскости проходит единственная интегральная кривая уравнения.

Используя полученные сведения, строим приближенно семейство интегральных кривых данного уравнения (рис. 8).

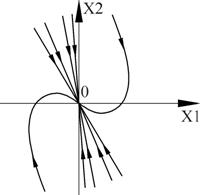
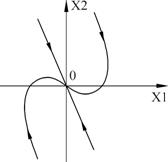
Замечание 2. Точки пересечения двух или нескольких изоклин могут быть особыми точками дифференциального уравнения (1), т.е. такими точками, в которых правая часть уравнения (1) не определена.

В точке пересекаются все изоклины данного уравнения (особая точка уравнения). С помощью полученных изоклин строим интегральные кривые (рис. 10).

Источник

ЛЕКЦИЯ 4

Модели, описываемые системами двух автономных дифференциальных уравнений.

Фазовая плоскость. Фазовый портрет. Метод изоклин. Главные изоклины. Устойчивость стационарного состояния. Линейные системы. Типы особых точек: узел, седло, фокус, центр. Пример: химические реакции первого порядка.

Наиболее интересные результаты по качественному моделированию свойств биологических систем получены на моделях из двух дифференциальных уравнений, которые допускают качественное исследование с помощью метода фазовой плоскости. Рассмотрим систему двух автономных обыкновенных дифференциальных уравнений общего вида

(4.1)

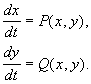
Область G может быть как неограниченной, так и ограниченной. Если переменные x, y имеют конкретный биологический смысл (концентрации веществ, численности видов) чаще всего область G представляет собой положительный квадрант правой полуплоскости:

Концентрации веществ или численности видов также могут быть ограничены сверху объемом сосуда или площадью ареала обитания. Тогда область значений переменных имеет вид:

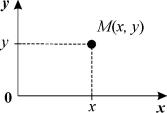
Изображающая точка на фазовой плоскости

Обратно, каждой паре переменных ( x, y) соответствует определенное состояние системы.

Рассмотрим плоскость с осями координат, на которых отложены значения переменных x,y. Каждая точка М этой плоскости соответствует определенному состоянию системы. Такая плоскость носит название фазовой плоскости и изображает совокупность всех состояний системы. Точка М(x,y) называется изображающей или представляющей точкой.

Совокупность фазовых траекторий при различных начальных значениях переменных дает легко обозримый «портрет» системы. Построение фазового портрета позволяет сделать выводы о характере изменений переменных x, y без знания аналитических решений исходной системы уравнений (4.1).

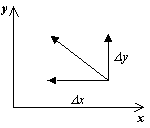
Для изображения фазового портрета необходимо построить векторное поле направлений траекторий системы в каждой точке фазовой плоскости. Задавая приращение D t>0, получим соответствующие приращения D x и D y из выражений:

Направление вектора dy/dx в точке ( x, y) зависит от знака функций P(x, y), Q(x, y) и может быть задано таблицей:

Задача построения векторного поля упрощается, если получить выражение для фазовых траекторий в аналитическом виде. Для этого разделим второе из уравнений системы (4.1) на первое:

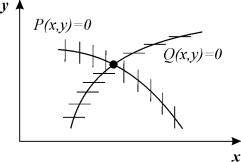
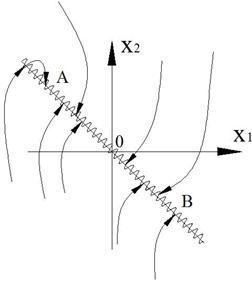
Для построения фазового портрета пользуются методом изоклин – на фазовой плоскости наносят линии, которые пересекают интегральные кривые под одним определенным углом. Уравнение изоклин легко получить из (4.2). Положим

Уравнение (4.3) определяет в каждой точке плоскости единственную касательную к соответствующей интегральной кривой за исключением точки, где P (x,y) = 0, Q ( x,y) = 0, в которой направление касательной становится неопределенным, так как при этом становится неопределенным значение производной:

Эта точка является точкой пересечения всех изоклин – особой точкой. В ней одновременно обращаются в нуль производные по времени переменных x и y.

Таким образом, в особой точке скорости изменения переменных равны нулю. Следовательно, особая точка дифференциальных уравнений фазовых траекторий (4.2) соответствует стационарному состоянию системы (4.1), а ее координаты – суть стационарные значения переменных x, y.

Особый интерес представляют главные изоклины:

dy/dx=0, P ( x,y) =0 – изоклина горизонтальных касательных и

Построив главные изоклины и найдя точку их пересечения (x,y), координаты которой удовлетворяют условиям:

мы найдем тем самым точку пересечения всех изоклин фазовой плоскости, в которой направление касательных к фазовым траекториям неопределенно. Это – особая точка, которая соответствует стационарному состоянию системы (рис. 4.2).

Система (4.1) обладает столькими стационарными состояниями, сколько точек пересечения главных изоклин имеется на фазовой плоскости.

Каждая фазовая траектория соответствует совокупности движений динамической системы, проходящих через одни и те же состояния и отличающихся друг от друга только началом отсчета времени.

Рис. 4.2. Пересечение главных изоклин на фазовой плоскости.

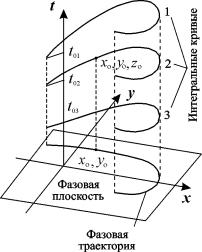
Таким образом, фазовые траектории системы – это проекции интегральных кривых в пространстве всех трех измерений x, y, t на плоскость x, y (рис.4.3).

Рис. 4.3. Траектории системы в пространстве ( x, y, t).

Если условия теоремы Коши выполнены, то через каждую точку пространства x, y, t проходит единственная интегральная кривая. То же справедливо, благодаря автономности, для фазовых траекторий: через каждую точку фазовой плоскости проходит единственная фазовая траектория.

Устойчивость стационарного состояния

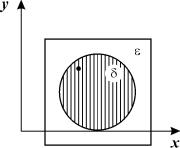
Пусть система находится в состоянии равновесия.

Тогда изображающая точка находится в одной из особых точек системы, в которых по определению:

Иллюстрация к определению устойчивости области e и d на плоскости ( x,y)

Для большого класса систем – грубых систем – характер поведения которых не меняется при малом изменении вида уравнений, информацию о типе поведения в окрестности стационарного состояния можно получить, исследуя не исходную, а упрощенную линеаризованную систему.

Рассмотрим систему двух линейных уравнений:

Здесь a, b, c, d — константы, x, y ‑ декартовы координаты на фазовой плоскости.

Общее решение будем искать в виде:

Подставим эти выражения в (4.4) и сократим на e l t :

(4.6)

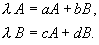
Алгебраическая система уравнений (4.6) с неизвестными A, B имеет ненулевое решение лишь в том случае, если ее определитель, составленный из коэффициентов при неизвестных, равен нулю:

Раскрывая этот определитель, получим характеристическое уравнение системы:

_(4.9)

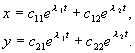
Для анализа характера возможных траекторий системы на фазовой плоскости используем линейное однородное преобразование координат, которое позволит привести систему к каноническому виду:

(4.1)

В этом случае коэффициенты преобразования действительны, мы переходим от действительной плоскости x,y к действительной плоскости ξ, η. Разделив второе из уравнений (4.10) на первое, получим :

Интегрируя это уравнение, находим :

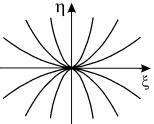
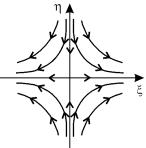
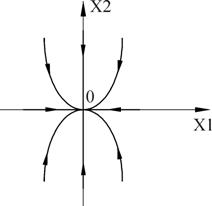
Все интегральные кривые (кроме оси η, которой соответствует ) касаются в начале координат оси ξ, которая также является интегральной кривой уравнения (4.11). Начало координат является особой точкой.

Такая особая точка, через которую проходят интегральные кривые, подобно тому, как семейство парабол проходит через начало координат, носит название узла (рис. 4.5)

Рис. 4.5. Особая точка типа узел на плоскости канонических координат ξ, η

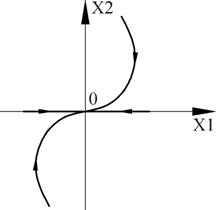
Интегрируя (4.14), находим

(4.15)

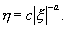
и система имеет своими состояниями равновесия все точки прямой :

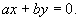
Рис. 4.7. Фазовый портрет системы, один из характеристических корней которой равен нулю, а второй отрицателен.

(4.16)

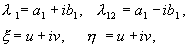
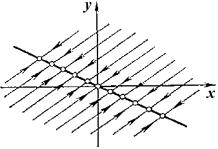
где a,b, и u,v – действительные величины. Можно показать, что преобразование от x,y к u,v является при наших предположениях действительным, линейным, однородным с детерминантом, отличным от нуля. В силу уравнений (4.10, 4.16) имеем :

(4.17)

где

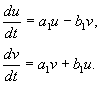
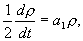
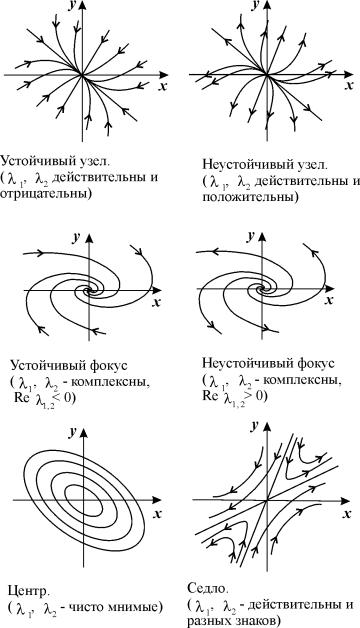
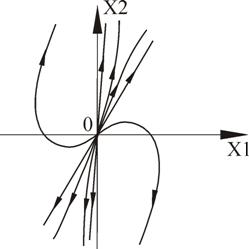
Таким образом, возможны шесть типов состояния равновесия в зависимости от характера корней характеристического уравнения (4.7). Вид фазовых траекторий на плоскости x, y для этих шести случаев изображен на рис. 4.9.

Рис. 4.9. Типы фазовых портретов в окрестности стационарного состояния для системы линейных уравнений (4.4).

Пять типов состояния равновесия грубые, их характер не изменяется при достаточно малых изменениях правых частей уравнений (4.4). При этом малыми должны быть изменения не только правых частей, но и их производных первого порядка. Шестое состояние равновесия – центр – негрубое. При малых изменениях параметров правой части уравнений он переходит в устойчивый или неустойчивый фокус.

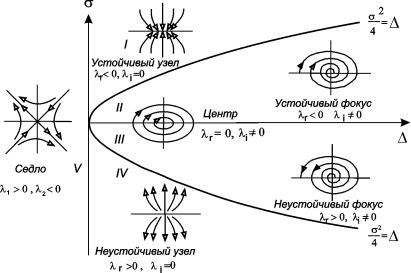
Бифуркационная диаграмма

Тогда характеристическое уравнение запишется в виде:

Рис. 4.10. Бифуркационная диаграмма

для системы линейных уравнений 4.4

На диаграмме видно, как могут проходить такие изменения. Если исключить особые случаи – начало координат, – то легко видеть, что седло может переходить в узел, устойчивый или неустойчивый при пересечении оси ординат. Устойчивый узел может перейти либо в седло, либо в устойчивый фокус, и т.д. Отметим, что переходы устойчивый узел – устойчивый фокус и неустойчивый узел – неустойчивый фокус не являются бифуркационными, так как топология фазового пространства при этом не меняется. Более подробно мы поговорим о топологии фазового пространства и бифуркационных переходах в лекции 6.

При бифуркационных переходах меняется характер устойчивости особой точки. Например, устойчивый фокус через центр может переходить в неустойчивый фокус. Эта бифуркация называется бифуркацией Андронова-Хопфа по именам исследовавших ее ученых. При этой бифуркации в нелинейных системах происходит рождение предельного цикла, и система становится автоколебательной (см. лекцию 8).

Пример. Система линейных химических реакций

Вещество Х притекает извне с постоянной скоростью, превращается в вещество Y и со скоростью, пропорциональной концентрации вещества Y, выводится из сферы реакции. Все реакции имеют первый порядок, за исключением притока вещества извне, имеющего нулевой порядок. Схема реакций имеет вид:

(4.14)

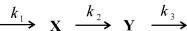
и описывается системой уравнений:

(4.15)

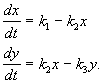
Стационарные концентрации получим, приравняв правые части нулю:

Рассмотрим фазовый портрет системы. Разделим второе уравнение системы (4.16) на первое. Получим:

Уравнение (4.17) определяет поведение переменных на фазовой плоскости. Построим фазовый портрет этой системы. Сначала нарисуем главные изоклины на фазовой плоскости. Уравнение изоклины вертикальных касательных:

Уравнение изоклины горизонтальных касательных:

Особая точка (стационарное состояние) лежит на пересечении главных изоклин.

Теперь определим, под каким углом пересекаются координатные оси интегральными кривыми.

Таким образом, тангенс угла наклона касательной к интегральным кривым y=y(x), пересекающим ось ординат x=0, отрицателен в верхней полуплоскости (вспомним, что переменные x, y имеют значения концентраций, и поэтому нас интересует только правый верхний квадрант фазовой плоскости). При этом величина тангенса угла наклона касательной увеличивается с удалением от начала координат.

При 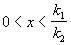тангенс угла наклона интегральных кривых, пересекающих ось абсцисс, положителен и увеличивается от нуля до бесконечности с увеличением x.

Рис. 4.12. Фазовый портрет системы линейных химических реакций (4.15)

Источник

2. ,

, , ,

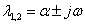
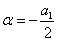
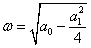
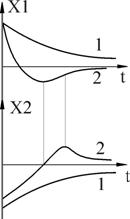
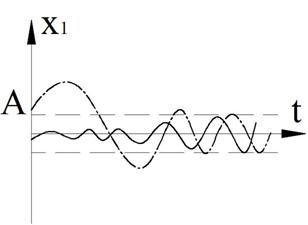
Рисунок 19 – Фазовый портрет и переходный процесс

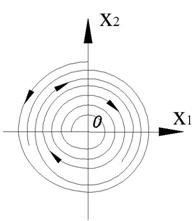
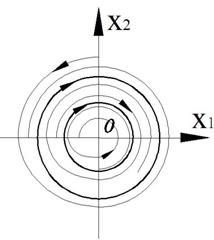
Фазовый портрет представляет собой логарифмическую спираль, сходящуюся к нулю.

Точка (0,0) – особая точка типа «устойчивый фокус».

3. ,

, , ,

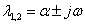
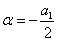
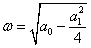
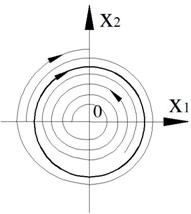
Фазовый портрет представляет собой логарифмическую спираль, рассходящуюся от нулю.

Точка (0,0) – особая точка типа «неустойчивый фокус».

4. ,

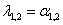
Рисунок 21 – Фазовый портрет

Рисунок 22 – Переходные процессы

Асимптоты: ,

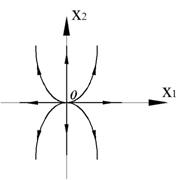
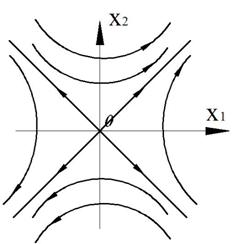
Точка (0,0) – особая точка типа «устойчивый узел».

Вырожденный случай получаем, когда корни одинаковы.

Если матрица в уравнении Коши имеет диагональный вид, то фазовый портрет имеет вид

Рисунок 24 – Частный случай фазового портрета системы

Если матрица имеет диагональный вид и корни равны, то имеем случай

5. ,

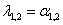
Рисунок 26 – Фазовый портрет

Рисунок 27 – Переходный процесс

Вырожденный случай получаем, когда корни одинаковы.

Рисунок 28 – Вырожденный неустойчивый узел

Если матрица в уравнении Коши имеет диагональный вид, то фазовый портрет имеет следующий вид

Если матрица имеет диагональный вид и корни равны, то имеем случай на рис. 35

6. ,

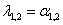
Рисунок 31 – Фазовый портрет

Рисунок 32 – Переходный процесс

Если матрица А имеет диагональный вид, то фазовый портрет изменится следующим образом.

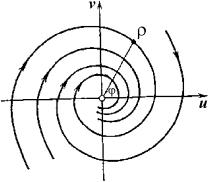
Для уточнения фазовых траекторий используется метод изоклин.

Изоклина – это линия, соединяющая точки фазовых траекторий с одинаковым наклоном касательных. Для линейных систем изоклины представляют собой прямые и проходят через точку (0;0).

Изоклина определяется следующим образом:

Рисунок 34 – Уточнение фазового портрета методом изоклин

Фазовые портреты нелинейных систем.

Неопределенность:

В отличие от линейных систем, в нелинейных системах могут быть и особые линии.

Особые точки те же: центр, узел, фокус, седло и т.д.

Особые линии: устойчивый предельный цикл (фазовая траектория замкнута), неустойчивый предельный цикл, линия устойчивого положения, сепаратрисса (линия, разделяющая области с разным видом фазовых траекторий) и т.д.

Для выявления вида особых точек уравнение системы линеаризуется в их окрестности, определяются корни характеристического уравнения линеаризованной системы.

Уравнение изоклин:

Типовые случаи фазовых портретов нелинейных систем.

1. Устойчивый предельный цикл (автоколебания).

Фазовая траектория стремится к предельному циклу, следовательно, цикл устойчив.

Рисунок 35 – Фазовый портрет

Рисунок 36 – Переходный процесс

В данном случае система неустойчива в малом (точка (0;0) – неустойчивый фокус), но устойчива – в большом. Т.е. в малых значениях она будет расходиться, а при больших начальных условиях

2. Неустойчивый предельный цикл.

Рисунок 37 – Фазовый портрет

Рисунок 38 – Переходный процесс

Система в малом становится устойчивой (точка (0;0) – неустойчивый фокус), а в большом – неустойчивой.

Практически, неустойчивый предельный цикл ограничивает область начальных условий, в пределах которой система устойчива.

3. Несколько предельных циклов.

Рисунок 39 – Фазовый портрет

Рисунок 40 – Переходный процесс

Внешний предельный цикл устойчив, внутренний – неустойчив.

Рисунок 41 – Особая линия типа «сепаратриса»

Сепаратрисcа – особая линия, разделяющая области с различным видом фазовых траекторий.

Три особых точки: «центр» и две типа «седло». Всего на фазовой плоскости образовано 5 областей.

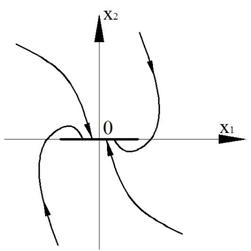
5. Отрезок установившихся состояний (отрезок покоя).

Фазовая траектория только входит в отрезок покоя. На отрезке скорость равна нулю (покой).

Рисунок 42 – Особая линия типа «отрезок покоя»

6. Скользящий процесс.

Рисунок 43 – Скользящий процесс

Если траектория приходит не на отрезок AB, то она преломляется на линии скользящего процесса и затем возвращается на отрезок.

При попадании на отрезок скользящего процесса, система начинает двигаться по линии скользящего процесса в направлении точки (0,0)

Практическое значение: в данном случае мы получаем желаемый переходный процесс с заданным законом движения. Это достижимо, если организовать соответствующее управление (нелинейный закон управления), что возможно далеко не всегда.

Рисунок 44 – Движение по линии скользящего процесса

В результате получаем процесс движения по отрезку скользящего процесса в виде колебаний относительно отрезка с амплитудой, стремящейся к нулю, и частотой, стремящейся к бесконечности.

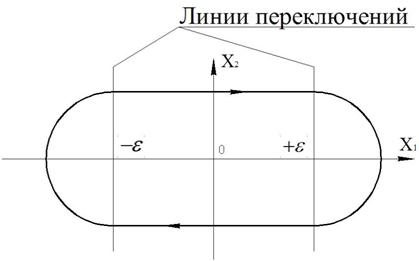
7. Линия переключений (нелинейный закон управления).

Рисунок 45 – Фазовый портрет системы

Пример. Построить фазовый портрет для системы, описываемой следующими уравнениями:

Условие 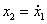не выполняется, следовательно направление фазовых траекторий может быть произвольным.

Разделим уравнение (2) на уравнение (1), получим дифференциальное уравнение фазовой траектории:

Особые точки и линии:

Решение дает 3 особые точки:

1) 2) 3)

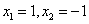
Для определения типа особых точек необходимо линеаризовать уравнение нелинейной системы в окрестности этих особых точек:

Далее символподразумевается, но не пишется.

1)

Для определения типа особой точки решаем характеристическое уравнение:

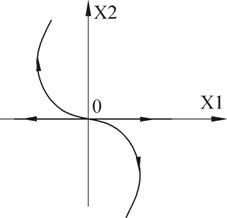
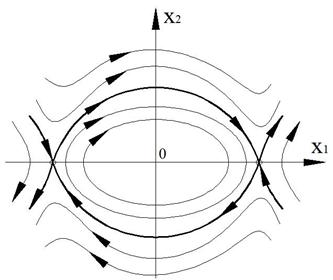
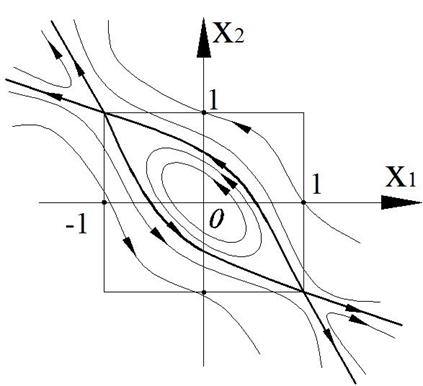
В итоге получаем чисто мнимые корни. Особая точка типа «центр» (фазовая траектория – эллипсы).

2)

Корни вещественные, разного знака. Особая точка типа «седло».

, k – коэффициент наклона асимптоты

Асимптоты действительны только в малой окрестности точки (1;-1)

3)

Далее аналогично пункту 2)

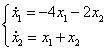
Определим направление фазовых траекторий: возьмем точку 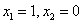и подставим в исходное нелинейное уравнение системы:

при с =1 (наклон касательной 45 о ): 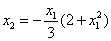, изоклина пройдет через все особые точки.

Таким образом, получаем фазовый портрет

Рисунок 46 – Фазовый портрет

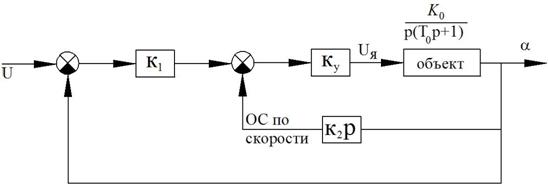
Изображение переходных процессов на фазовой плоскости на примере электромеханического следящего привода.

ДПТ – двигатель постоянного тока

ДС – датчик скорости

— механическая связь

— электрическая связь

— угол поворота выходного вала редуктора

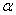
Рисунок 47 – Структурная схема электромеханического следящего привода

Будем считать, что характеристики ДС и ДП линейные.

Пример 1. Следящий привод. Нагрузка: инерционная и вязкое трение.

Рисунок 48 – Структурная схема механической части объекта

— момент инерции двигателя

— момент инерции нагрузки

— передаточное отношение редуктора

— вязкое трение нагрузки

— коэффициент противоЭДС

— коэффициент усиления по моменту

— уравнение ДПТ

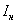
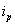
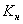
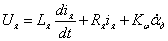
Введем допущение: в рабочем режиме ДПТ(в реальной жизни – гистерезис)

Введем допущение: пренебрегаем электрической постоянной двигателя (на два порядка меньше, чем электромеханическая постоянная).

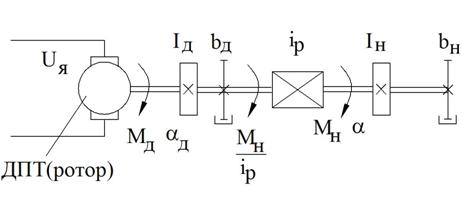
Уравнение моментов, приведенных к валу двигателя:

, где

Рисунок 49 – Объект управления

— описание объекта управления (интегрирующее звено с запаздыванием)

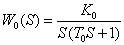
Необходимо найти уравнение регулятора:

Рисунок 50 – Пропорциональный интегральный регулятор

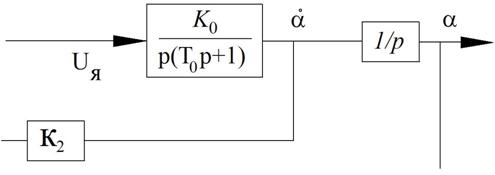
Обратная связь по скорости математически представлена верно, но на практике так делать нельзя из-за шумов (при дифференцировании не будет асимптоты).

При моделировании для исключения шумов необходимо изменить схему следующим образом:

Рисунок 51 – Изменения в схеме для моделирования

Уравнение регулятора с усилителем:

,

— колебательное звено.

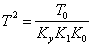
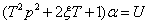
Обозначим:

Фазовые портреты при U=0

В соответствии уравнение линеаризованной системы принимает следующий вид:

2) Вычисления коэффициентов гармонической линеаризации для несимметричных колебаний

Причины несимметричных колебаний:

1) Несимметричные входные колебания;

Решения будем искать в виде: x = x 0 + asin(ωt) = x 0 +x*, где x*= asin(ωt)

Уравнение системы можно разбить на 2 уравнения: для постоянной составляющей и для гармонического сигнала

3) Вычисление коэффициентов гармонической линеризации для симметричных колебаний

Упрощения: для однозначной нечётной симметричной функции F(x) коэффициент q`=0

Рисунок 96. Случай а)

Рисунок 97. Случай б)

Рисунок 98. Случай в)

Рисунок 99. Случай г)

Рисунок 100. Случай д)

Чтобы распечатать файл, скачайте его (в формате Word).

Источник