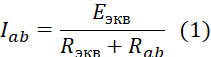Что такое метод эквивалентного генератора

23.09.202328.09.2023 admin 0 Comments

Метод эквивалентного генератора

Метод эквивалентного генератора применяется для определения тока одной из ветвей электрической цепи в том случае, когда расчет всей схемы не требуется. В основу метода положена теорема об активном двухполюснике (теорема Гельмгольца-Тевенена). Основная идея метода заключается в том, что часть цепи, параметры которой определять нет необходимости, заменяется эквивалентным генератором с известной эдс и сопротивлением. Метод часто применяется для расчета режима электрической цепи.

Алгоритм состоит из следующих шагов:

Метод эквивалентного генератора: примеры решения

Рассмотрим пример расчета электрической схемы методом эквивалентного генератора (рисунок 1).

Рис. 1. Метод эквивалентного генератора

Допустим, что необходимо рассчитать ток I_ab через резистор R4. Тогда преобразования схема будет иметь вид, представленный на рисунке 2.

Рис. 2. Эквивалентная электрическая схема

После преобразования ток через резистор R_ab (R4) определяется по формуле

Для того, чтобы рассчитать значения Еэкв и Rэкв необходимо рассмотреть режим холостого хода генератора. Для этого необходимо обеспечить его работу без нагрузки, то есть условно отсоединить от цепи исследуемую ветвь ab (рисунок 3).

Рис. 3. Режим холостого хода генератора

Для представленной схемы напряжение Еэкв будет равно

Далее требуется определить эквивалентное сопротивление. Для этого воспользуемся методом пассивного двухполюсника. В этом случае необходимо исключить из схемы источник эдс и найти общее сопротивление цепи (рисунок 4).

Рис. 4. Схема без источника эдс

Эквивалентное сопротивление полученной схемы определяется по формуле

Теперь можно определить ток, проходящий через резистор ab согласно выражению (1).

Источник

Что такое метод эквивалентного генератора

Метод эквивалентного генератора, основанный на теореме об активном двухполюснике (называемой также теоремой Гельмгольца-Тевенена), позволяет достаточно просто определить ток в одной (представляющей интерес при анализе) ветви сложной линейной схемы, не находя токи в остальных ветвях. Применение данного метода особенно эффективно, когда требуется определить значения тока в некоторой ветви для различных значений сопротивления в этой ветви в то время, как в остальной схеме сопротивления, а также ЭДС и токи источников постоянны.

Теорема об активном двухполюснике формулируется следующим образом: если активную цепь, к которой присоединена некоторая ветвь, заменить источником с ЭДС, равной напряжению на зажимах разомкнутой ветви, и сопротивлением, равным входному сопротивлению активной цепи, то ток в этой ветви не изменится.

Ход доказательства теоремы иллюстрируют схемы на рис. 1.

Указанные в теореме ЭДС и сопротивление можно интерпретировать как соответствующие параметры некоторого эквивалентного исходному активному двухполюснику генератора, откуда и произошло название этого метода.

Таким образом, в соответствии с данной теоремой схему на рис. 2,а, где относительно ветви, ток в которой требуется определить, выделен активный двухполюсник А со структурой любой степени сложности, можно трансформировать в схему на рис. 2,б.

Отсюда ток находится, как:

Что такое метод эквивалентного генератора. Смотреть фото Что такое метод эквивалентного генератора. Смотреть картинку Что такое метод эквивалентного генератора. Картинка про Что такое метод эквивалентного генератора. Фото Что такое метод эквивалентного генератора

(1)

где — напряжение на разомкнутых зажимах a-b.

Уравнение (1) представляет собой аналитическое выражение метода эквивалентного генератора.

Параметры эквивалентного генератора (активного двухполюсника) могут быть определены экспериментальным или теоретическим путями.

В первом случае, в частности на постоянном токе, в режиме холостого хода активного двухполюсника замеряют напряжение на его зажимах с помощью вольтметра, которое и равно . Затем закорачивают зажимы a и b активного двухполюсника с помощью амперметра, который показывает ток (см. рис. 2,б). Тогда на основании результатов измерений .

В принципе аналогично находятся параметры активного двухполюсника и при синусоидальном токе; только в этом случае необходимо определить комплексные значения и .

При теоретическом определении параметров эквивалентного генератора их расчет осуществляется в два этапа:

1. Любым из известных методов расчета линейных электрических цепей определяют напряжение на зажимах a-b активного двухполюсника при разомкнутой исследуемой ветви.

2. При разомкнутой исследуемой ветви определяется входное сопротивление активного двухполюсника, заменяемого при этом пассивным. Данная замена осуществляется путем устранения из структуры активного двухполюсника всех источников энергии, но при сохранении на их месте их собственных (внутренних) сопротивлений. В случае идеальных источников это соответствует закорачиванию всех источников ЭДС и размыканию всех ветвей с источниками тока.

Сказанное иллюстрируют схемы на рис. 3, где для расчета входного (эквивалентного) сопротивления активного двухполюсника на рис. 3,а последний преобразован в пассивный двухполюсник со структурой на рис. 3,б. Тогда согласно схеме на рис. 3,б

В качестве примера использования метода эквивалентного генератора для анализа определим зависимость показаний амперметра в схеме на рис. 4 при изменении сопротивления R переменного резистора в диагонали моста в пределах . Параметры цепи Е=100 В; R1=R4=40 Ом; R2=R3=60 Ом.

В соответствии с изложенной выше методикой определения параметров активного двухполюсника для нахождения значения перейдем к схеме на рис. 5, где напряжение на разомкнутых зажимах 1 и 2 определяет искомую ЭДС . В данной цепи

Для определения входного сопротивления активного двухполюсника трансформируем его в схему на рис. 6.

Со стороны зажимов 1-2 данного пассивного двухполюсника его сопротивление равно:

Таким образом, для показания амперметра в схеме на рис. 4 в соответствии с (1) можно записать

(2)

Задаваясь значениями R в пределах его изменения, на основании (2) получаем кривую на рис.7.

В качестве примера использования метода эквивалентного генератора для анализа цепи при синусоидальном питании определим, при каком значении нагрузочного сопротивления в цепи на рис. 8 в нем будет выделяться максимальная мощность, и чему она будет равна.

Параметры цепи: ; .

В соответствии с теоремой об активном двухполюснике обведенная пунктиром на рис. 8 часть схемы заменяется эквивалентным генератором с параметрами

В соответствии с (1) для тока через можно записать

откуда для модуля этого тока имеем

(3)

Анализ полученного выражения (3) показывает, что ток I, а следовательно, и мощность будут максимальны, если ; откуда , причем знак “-” показывает, что нагрузка имеет емкостный характер.

и .

Данные соотношения аналогичны соответствующим выражениям в цепи постоянного тока, для которой, как известно, максимальная мощность на нагрузке выделяется в режиме согласованной нагрузки, условие которого .

Таким образом, искомые значения и максимальной мощности: .

Теорема вариаций применяется в тех случаях, когда требуется рассчитать, насколько изменятся токи или напряжения в ветвях схемы, если в одной из ветвей этой схемы изменилось сопротивление.

Выделим на рис. 9,а некоторые ветви с токами и , а остальную часть схемы обозначим активным четырехполюсником А. При этом, полагаем что проводимости и известны.

Пусть сопротивление n-й ветви изменилось на . В результате этого токи в ветвях схемы будут соответственно равны и (рис. 9,б). На основании принципа компенсации заменим источником с ЭДС . Тогда в соответствии с принципом наложения можно считать, что приращения токов и вызваны в схеме на рис. 9,в, в которой активный четырехполюсник А заменен на пассивный П.

Для этой цепи можно записать

и .

Полученные соотношения позволяют определить изменения токов в m-й и n-й ветвях, вызванные изменением сопротивления в n-й ветви.

Контрольные вопросы и задачи

Ответ: .

Источник

Суть метода эквивалентного генератора

Метод эквивалентного генератора (МЭГ) применяется, когда есть некая нагрузка, подключённая к сложной активной цепи. При этом активная цепь сама по себе интереса не представляет, но необходимо учесть её влияние на нагрузку, на которую направлен фокус. С помощью данного метода активная цепь преобразуется в очень простой вид – в одну ветвь с эквивалентной ЭДС E_экв и с эквивалентным сопротивлением Z_экв.

Воспользуйтесь программой онлайн-расчёта электрических цепей. Программа позволяет рассчитывать электрические цепи по закону Ома, по законам Кирхгофа, по методам контурных токов, узловых потенциалов и эквивалентного генератора, а также рассчитывать эквивалентное сопротивление цепи относительно источника питания.

Суть метода эквивалентного генератора [1]

Пример того, как это делается, приведён на рис. 1. Самое важное здесь то, что ток в нагрузке что в исходной цепи, что в преобразованной, одинаковый. Именно в этом смысле эквивалентный генератор и эквивалентен исходной активной цепи.

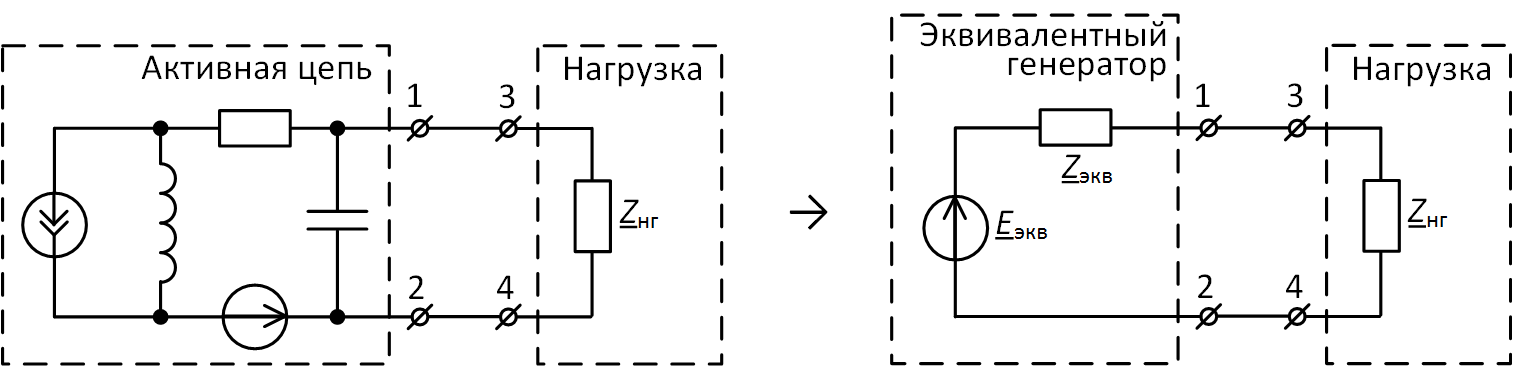
Рис. 1. Преобразование активной цепи в эквивалентный генератор

МЭГ применяется для решения самых разнообразных задач. Например, он используется в электроэнергетике, когда нужно рассчитать различные режимы сети. Конкретно используется для того, чтобы эквивалентировать всю внешнюю сеть по отношению к рассчитываемой, и тем самым упростить расчёт. Также часто бывает, что о внешней сети вообще мало что известно, и в этих условиях расчётчики просто вынуждены довольствоваться одним только эквивалентным генератором.

Эквивалентная ЭДС E_экв и с эквивалентное сопротивление Z_экв в зависимости от решаемой задачи могут быть определены двумя способами:

Первым способом можно воспользоваться только тогда, когда вся активная цепь перед глазами и известны все её параметры. А когда эквивалентируемая цепь – это «чёрный ящик», на котором можно проводить опыты, работает второй способ. В чём заключаются оба эти способа – очень важная информация для усвоения каждого изучающего ТОЭ, но намного важней знания о том, почему они работают. Поэтому далее подробно рассмотрим из чего именно вытекает МЭГ.

Возьмём пример по рис. 1 и для начала изолируем эквивалентируемую активную цепь от нагрузки (рис. 2). Это будет режим холостого хода, когда тока в нагрузке нет. В этом режиме нас интересует напряжение U_хх между выводами 1 и 2. Такое же напряжение будет между выводами 1 и 3, если соединить между собой выводы 2 и 4 (см. рис. 3), поскольку ток в нагрузке при этом останется равным нулю и падение напряжения между выводами 3 и 4 также будет нулевым.

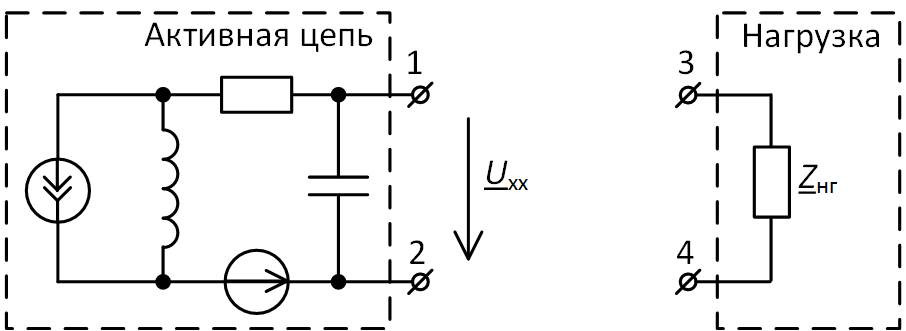
Рис. 2. Холостой ход эквивалентируемой цепи

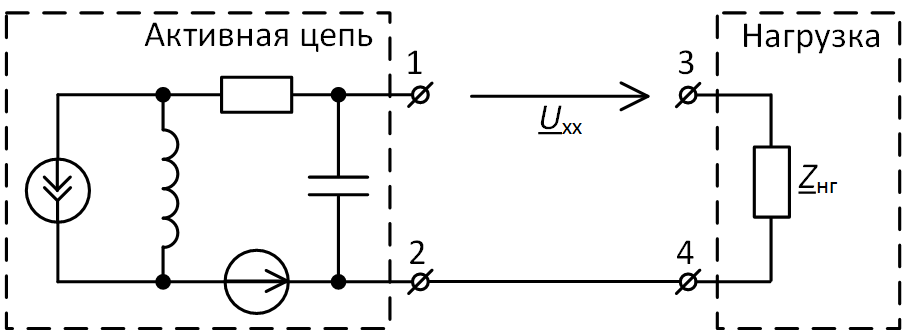
Рис. 3. Соединение выводов 2 и 4

Теперь очень важная мысль: если между выводами 1 и 3 включить ЭДС, равную U_хх, как это показано на рис. 4, то в результате ничего не изменится. Это очевидно, ведь такая ЭДС пытается поддержать между выводами 1 и 3 напряжение U_хх, а это было так и до её включения.

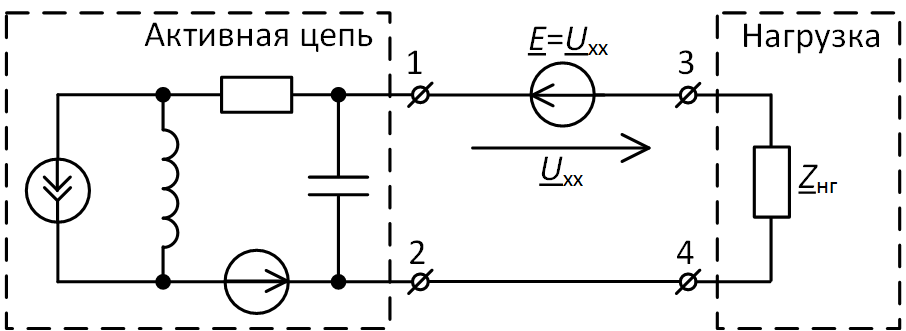
Рис. 4. Включение между выводами 1 и 3 ЭДС, равной U_хх

Далее, если рядом включить ещё такую же ЭДС, но с противоположным направлением, то в итоге получится исходная активная цепь с подключённой к ней нагрузке, как на рис. 1. Всё это проиллюстрировано на рис. 5.

Рис. 5. Включение между выводами 1 и 3 ещё одной такой же ЭДС с противоположным направлением

Применим принцип наложения и разложим получившуюся цепь с двумя ЭДС между выводами 1 и 3 на две части. Распределим между этими двумя частями все имеющиеся источники тока и ЭДС так, как это показано на рис. 6 (вспомним, что по принципу наложения исключаемые из одной из частей источники тока должны разрываться, а источники ЭДС – закорачиваться).

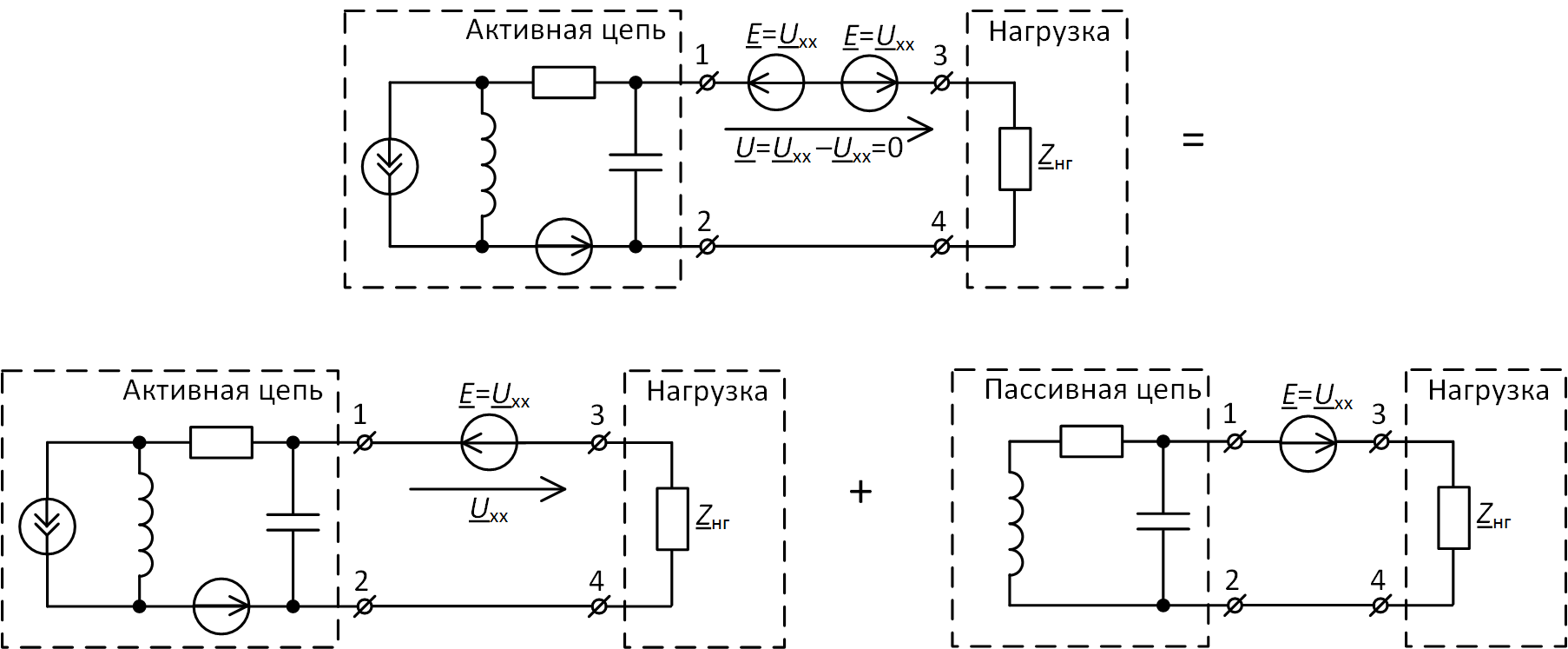
Рис. 6. Разделение активной цепи с нагрузкой на две части

Что имеем в итоге? Одну из частей мы уже видели на рис. 4, с точки зрения нагрузки это то же самое, что и на рис. 2, т.е. холостой ход. Для этой части ток в нагрузке получается нулевым, поэтому далее её можно исключить из рассмотрения. И выходит, что весь ток в нагрузке создаётся второй частью разделившейся цепи, она оказывается ей эквивалентной.

Далее дело техники преобразовать получившуюся пассивную цепь в эквивалентное сопротивление, затем объединить её с единственной в этой цепи ЭДС и получить таким образом то, что называется эквивалентным генератором (рис. 7).

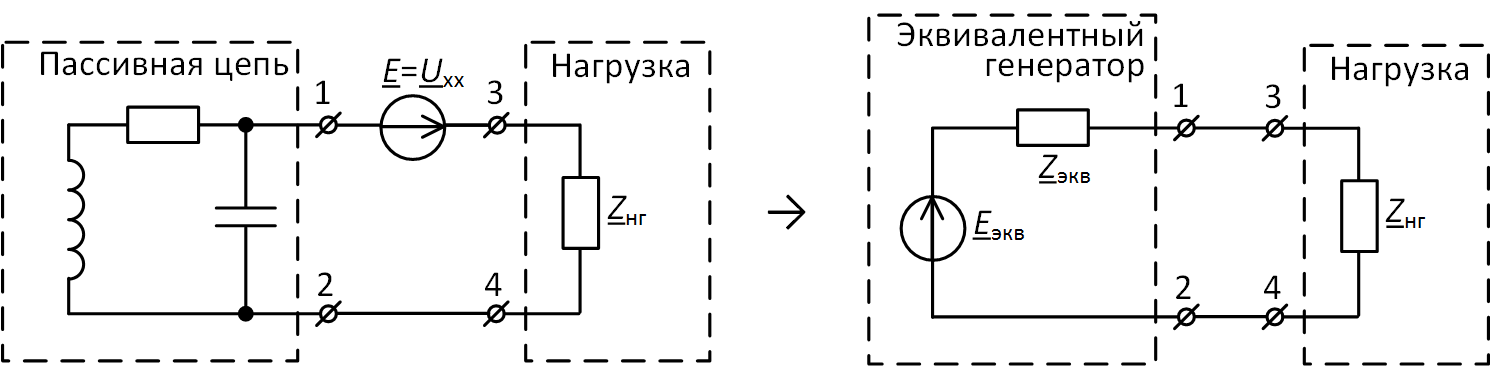
Рис. 7. Готовый эквивалентный генератор