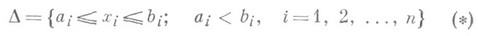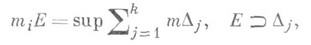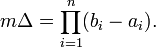Что такое мера жордана

Мера Жордана

Мера Жордана — один из способов формализации понятия длины, площади и -мерного объёма в -мерном евклидовом пространстве.

Содержание

Построение

Мера Жордана параллелепипеда в определяется как произведение

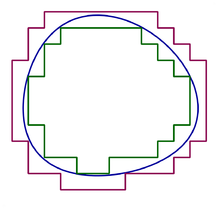
Для ограниченного множества определяются:

здесь — параллелепипеды описанного выше вида.

Множество называется измеримым по Жордану (квадрируемым при , кубируемым при ), если . В этом случае мера Жордана равна .

Свойства

История

Приведённое понятие меры ввели Пеано (1887) и Жордан (1892). Впоследствии понятие было обобщено Лебегом на более широкий класс множеств.

Пример множества, неизмеримого по Жордану

Рассмотрим меру Жордана , определённую на и пусть — множество точек единичного квадрата. Пусть — множество, состоящее из всех точек множества с рациональными координатами, тогда — неизмеримое по Жордану множество, так как , то есть верхняя и нижняя мера Жордана не совпадают.

Литература

См. также

Полезное

Смотреть что такое «Мера Жордана» в других словарях:

МЕРА — множества, обобщение понятия длины отрезка, площади фигуры, объема тела, интуитивно соответствующее массе множества при нек ром распределении массы по пространству. Понятие М. множества возникло в теории функций действительного переменного в… … Математическая энциклопедия

Мера — в Викисловаре? … Википедия

Мера вероятности — Мера качественная и/или количественная пропорция соотношения истин. Во многом пропорция устанавливается произвольно. Термины Мера (в метрологии) синоним единицы измерения. Мера внесистемная русская единица объёма. Мера (философия) философский… … Википедия

Мера Лебега — на мера, являющаяся продолжением меры Жордана на более широкий класс множеств, была введена Лебегом в 1902 году. Содержание 1 Построение меры на прямой 1.1 … Википедия

ЖОРДАНА МЕРА — параллелепипеда в Rn объем этого параллелепипеда. Для ограниченного множества определяются: внешняя мера Жордана и внутренняя мера Жордана где Dj попарно не пересекаются (здесь Dj параллелепипеды вида (*J). Множество Еназ. измеримым по Жордану… … Математическая энциклопедия

Мера множества — У этого термина существуют и другие значения, см. Мера. Мера множества неотрицательная величина, интуитивно интерпретируемая как размер (объем) множества. Собственно, мера это некоторая числовая функция, ставящая в соответствие каждому… … Википедия

Жорданова мера — Мера Жордана один из способов формализации понятия длины, площади и n мерного обьёма в n мерном евклидовом пространстве. Содержание 1 Построение 2 Свойства 3 История … Википедия

Конечно-аддитивная мера — Мера общее название различных типов обобщений понятий евклидовой длины, площади и n мерного объёма для более общих пространств. Если обратное не указано явно, то обычно подразумевается счётно аддитивная мера. Содержание 1 Определения 1.1 Конечно … Википедия

Конечно аддитивная мера — Мера общее название различных типов обобщений понятий евклидовой длины, площади и n мерного объёма для более общих пространств. Если обратное не указано явно, то обычно подразумевается счётно аддитивная мера. Содержание 1 Определения 1.1 Конечно … Википедия

Разложение Хана-Жордана — Заряд вещественнозначная конечно аддитивная функция множества, определённая на некоторой σ алгебре, (например, борелевских подмножеств). В отличие от обычной меры под которой, обычно понимают положительную σ аддитивную функцию множества, заряд… … Википедия

Источник

ЖОРДАНА МЕРА

в R n объем этого параллелепипеда.

Для ограниченного множества определяются: внешняя мера Жордана

и внутренняя мера Жордана

где В этом случае Ж. м. равна mE=m_eE=m_iE.

Ограниченное множество измеримо по Жордану тогда и только тогда, когда его граница имеет Ж. м. нуль (или, что равносильно, когда его граница имеет Лебега меру нуль).

Приведенное понятие меры ввели Дж. Пеано [1] и К. Жордан [2]. Внешняя Ж. м. одна и та же для Еи Е( замыкания множества Е )и равна Бореля мере Е. Измеримые по Жордану множества образуют кольцо множеств, на к-ром Ж. м. конечно аддитивная функция. См. также Квадрируемость.

Лит.:[1] Реanо G., Applicazioni geometriche del calcolo infinitesimale, Torino, 1887; [2] Jordan C, «J. math, pures et appl.», 1892, t. 8, p. 69-99; [3] Никольский С. М., Курс математического анализа, т. 2, М., 1973; [4] Колмогоров А. Н., Фомин С. В., Элементы теории функций и функционального анализа, 4 изд., М., 1976.

Полезное

Смотреть что такое «ЖОРДАНА МЕРА» в других словарях:

Мера Жордана — Мера Жордана один из способов формализации понятия длины, площади и мерного объёма в мерном евклидовом пространстве. Содержание 1 Построение 2 Свойства … Википедия

МЕРА — множества, обобщение понятия длины отрезка, площади фигуры, объема тела, интуитивно соответствующее массе множества при нек ром распределении массы по пространству. Понятие М. множества возникло в теории функций действительного переменного в… … Математическая энциклопедия

Мера Лебега — на мера, являющаяся продолжением меры Жордана на более широкий класс множеств, была введена Лебегом в 1902 году. Содержание 1 Построение меры на прямой 1.1 … Википедия

Мера — в Викисловаре? … Википедия

Мера вероятности — Мера качественная и/или количественная пропорция соотношения истин. Во многом пропорция устанавливается произвольно. Термины Мера (в метрологии) синоним единицы измерения. Мера внесистемная русская единица объёма. Мера (философия) философский… … Википедия

Мера множества — У этого термина существуют и другие значения, см. Мера. Мера множества неотрицательная величина, интуитивно интерпретируемая как размер (объем) множества. Собственно, мера это некоторая числовая функция, ставящая в соответствие каждому… … Википедия

Жорданова мера — Мера Жордана один из способов формализации понятия длины, площади и n мерного обьёма в n мерном евклидовом пространстве. Содержание 1 Построение 2 Свойства 3 История … Википедия

Конечно-аддитивная мера — Мера общее название различных типов обобщений понятий евклидовой длины, площади и n мерного объёма для более общих пространств. Если обратное не указано явно, то обычно подразумевается счётно аддитивная мера. Содержание 1 Определения 1.1 Конечно … Википедия

Конечно аддитивная мера — Мера общее название различных типов обобщений понятий евклидовой длины, площади и n мерного объёма для более общих пространств. Если обратное не указано явно, то обычно подразумевается счётно аддитивная мера. Содержание 1 Определения 1.1 Конечно … Википедия

Разложение Хана-Жордана — Заряд вещественнозначная конечно аддитивная функция множества, определённая на некоторой σ алгебре, (например, борелевских подмножеств). В отличие от обычной меры под которой, обычно понимают положительную σ аддитивную функцию множества, заряд… … Википедия

Источник

Жорданова мера

Содержание

Построение

Мера Жордана mΔ параллелепипеда 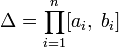в определяется как произведение

Для ограниченного множества 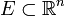определяются:

здесь 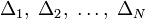— параллелепипеды описанного выше вида.

Свойства

История

Приведённое понятие меры ввели Пеано (1887) и Жордан (1892). Впоследствии понятие было обобщено Лебегом на более широкий класс множеств.

Литература

См. также

Полезное

Смотреть что такое «Жорданова мера» в других словарях:

СПЕКТРАЛЬНАЯ МЕРА — унитальный гомоморфизм нек рой булевой алгебры множеств в булеву алгебру проекторов в банаховом пространстве. Всякий оператор Тв банаховом пространстве Xопределяет С. м. на совокупности открыто замкнутых подмножеств его спектра по формуле где Г… … Математическая энциклопедия

Жордан, Мари Энмон Камиль — Мари Энмон Камиль (Камилл) Жордан Marie Ennemond Camille Jordan Дата рождения … Википедия

ДВУХ КОНСТАНТ ТЕОРЕМА — пусть D конечносвязная жорданова область на плоскости комплексного переменного z, w(z) регулярная аналитич. функция в D, удовлетворяющая неравенству причем на нек рой дуге a. границы дD выполняется соотношение тогда в каждой точке z множества где … Математическая энциклопедия

КВАДРИРУЕМОСТЬ — измеримость по Жордану множества на плоскости (см. Жордана мера). Не всякая область (т. е. открытое связное множество) и даже но всякая жорданова область (т. е. область, имеющая своей границей простую замкнутую кривую) квадрируема. С другой… … Математическая энциклопедия

ПЛАТО ЗАДАЧА — задача нахождения минимальной поверхности (м. п.) с заранее заданной границей Г. Впервые такая задача была поставлена Ж. Лагранжем (J. Lagrange, 1760), к рый свел ее в классе поверхностей вида z=z( х, у).к решению уравнения Эйлера Лагранжа м. п.… … Математическая энциклопедия

Жордан Мари Энмон Камиль — Камиль Жордан Мари Энмон Камиль (Камилл) Жордан (фр. Marie Ennemond Camille Jordan, 5 января 1838 22 января 1922) французский математик, известный благодаря своим фундаментальным работам в теории групп и «Курсу анализа». Он родился в Лионе и… … Википедия

Камилл Жордан — Камиль Жордан Мари Энмон Камиль (Камилл) Жордан (фр. Marie Ennemond Camille Jordan, 5 января 1838 22 января 1922) французский математик, известный благодаря своим фундаментальным работам в теории групп и «Курсу анализа». Он родился в Лионе и… … Википедия

Мари Энмон Камиль Жордан — Камиль Жордан Мари Энмон Камиль (Камилл) Жордан (фр. Marie Ennemond Camille Jordan, 5 января 1838 22 января 1922) французский математик, известный благодаря своим фундаментальным работам в теории групп и «Курсу анализа». Он родился в Лионе и… … Википедия

Источник

Понятие объема в n-мерном пространстве (мера Жордана). Измеримые множества

Понятие объема в n-мерном пространстве (мера Жордана). Измеримые множества

Понятие объема в n-мерном пространстве (мера Жордана). Измеримые множества. кратко напомним основные понятия, связанные с определением n-мерного объема (площади в случае n = 2), и дадим новое определение. Разделение понятия на заданный объем (меру).Это отличается от того, что было введено ранее (см. раздел 31.1). HN в N-мерном евклидовом пространстве (n = 1, 2,3,…И чтобы. Эта точка, как обычно, x-(x1,…хп).Где XI, 1 = 1,2,…n-это Координата точки x в фиксированной системе координат. Неотрицательное целое число k(k = 0, 1,…Исправить это.)Первая координатная ось ((=1, 2,…, n), то есть координаты X!= …х ^ р-x1n = … Рассмотрим множество точек x с = X / r =0. х,= 1 () РМ, М-0、±1、±2、…Через эту точку с координатами в виде Гиперплоскость размерности η-1, ортогональная этой оси.

Кроме того, множество лежит находится в многограннике»строго внутри», то есть оно не пересекается. Людмила Фирмаль

Объем его Р-размерности определяется уравнением 11 (44.2)） В Очевидно, что p5-неотрицательное число или+ oo. Здесь пусть это произвольное множество% N. 5 * = 5k(E) представляет собой множество точек всех X-мерных кубов ранга k, которые все находятся в E, а 3k = 3k (E) представляет собой множество точек всех X-мерных кубов ранга k, которые пересекают множество E, соответственно…） 8К(Е)= Г Эл、 ？л = я 8К (Е)= Г 2А, рН Людмила Фирмаль

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник

Математическая энциклопедия

Смотреть значение Жордана Мера в других словарях

Мера — меры, ж. 1. Единица измерения протяжения или емкости. длины. веса. Меры сыпучих тел. Кубические меры. 2. Предел, граница, размер. Чудится, будто. голубая зеркальная дорога.
Толковый словарь Ушакова

Мера — Действие, направленное для достижения чего-либо; наказание (обычно во мн. числе).
Активная, безотлагательная, благоразумная, вынужденная, высшая, действенная, демократическая.
Словарь эпитетов

Мера Ж. — 1. Единица измерения. 2. Старинная русская единица емкости для сыпучих тел, равная приблизительно одному пуду зерна. // Сосуд для измерения сыпучих тел, вмещающий такое.
Толковый словарь Ефремовой

Мера Наказания — наказание, назначаемое судом подсудимому на основании нормы уголовного права.
Экономический словарь

Мера Потребления — мера, доля национального дохода, которую должен получить каждый работающий член общества, в соответствии с затраченным трудом.
Экономический словарь

Мера Предосторожности — действие, предпринимаемое для ограждения интересов страхователя или предотвращения нежелательных рисков.
Экономический словарь

Мера Пресечения — метод пресечения попыток подозреваемого уклониться от явки в
органы дознания, в суд, помешать установлению истины или продолжить преступную деятельность. В качестве.
Экономический словарь

Мера Рентабельности (profit Margin) — Соотношение прибыли и выручки.
Прибыль может как включать, так и не включать экстраординарные события и показываться в
размере как до, так и после уплаты налогов.
Экономический словарь

Мера Торговая — установленное биржей минимальное количество ценных бумаг, образующих одну партию.
Экономический словарь

Мера Труда — мера участия каждого работника в совокупном общественном труде.
Экономический словарь

Часть, Доля, Мера, Единица — В общем значении: единица измерения. Любая часть Количества, принимаемая в качестве стандарта измерений или обмена. Например, на рынке товарно-сырьевой продукции единицей.
Экономический словарь

Мера — Общеславянское слово, образованное от индоевропейской основы те. В древнеиндийском находим mati – «мерит», в латинском – metior («мерю, измеряю»). Родственные слова: метр, английское measure («мера»).
Этимологический словарь Крылова

Мера — в России емкость для измерения жидких и сыпучих тел. Обычно равначетверику (26,24 л).
Большой энциклопедический словарь

Мера Пресечения — в уголовном процессе способ пресечения попытокобвиняемого уклониться от явки в следственные органы и в суд, помешатьустановлению истины или продолжить преступную.
Большой энциклопедический словарь

Мера — — в России емкость для измерения жидких и сыпучих тел, обычно равна четверику — 26,24 п.
Исторический словарь

Мера — Русская мера вместимости жидкостей и сыпучих тел, равная четверику = 26,24 л.
Словарь мер и весов

Мера Различий — основных тенденций социальных групп отражает различия степени или уровня влияния, оказываемого независимой переменной.
Социологический словарь

Источник