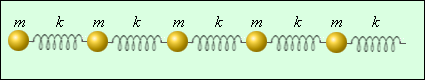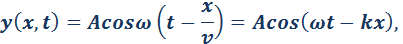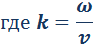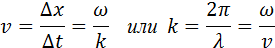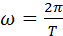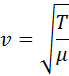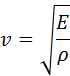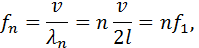Что такое механические волны

Механические волны

Когда в каком-нибудь месте твердой, жидкой или газообразной среды происходит возбуждение колебаний частиц, результатом взаимодействия атомов и молекул среды становится передача колебаний от одной точки к другой с конечной скоростью.

Волна – это процесс распространения колебаний в среде.

Виды механических волн

Различают следующие виды механических волн:

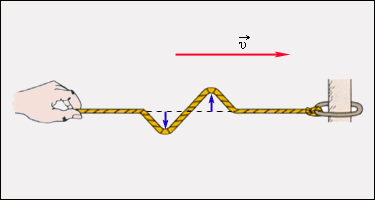
Поперечная волна: частицы среды смещаются в направлении, перпендикулярном направлению распространения механической волны.

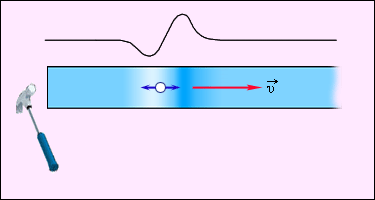
Продольная волна: частицы среды смещаются в направлении распространения механической волны.

Интересно, что волны на поверхности жидкости включают в себя и поперечную, и продольную компоненты.

Укажем важное уточнение: когда механические волны распространяются, они переносят энергию, форму, но не переносят массу, т.е. в обоих видах волн переноса вещества в направлении распространения волны не происходит. Распространяясь, частицы среды совершают колебания около положений равновесия. При этом, как мы уже сказали, волны переносят энергию, а именно энергию колебаний от одной точки среды к другой.

Модель твердого тела

Отличительная особенность продольных волн заключается в том, что они способны распространяться в любых средах: твердых, жидких и газообразных.

Если в указанной модели твердого тела один или несколько шариков получают смещение перпендикулярно всей цепочке, можно говорить о возникновении деформации сдвига. Пружины, получившие деформацию в результате смещения, будут стремиться вернуть смещенные частицы в положение равновесия, а на ближайшие несмещенные частицы начнет оказываться влияние упругих сил, стремящихся отклонить эти частицы от положения равновесия. Итогом станет возникновение поперечной волны в направлении вдоль цепочки.

В жидкой или газообразной среде упругая деформация сдвига не возникает. Смещение одного слоя жидкости или газа на некоторое расстояние относительно соседнего слоя не приведет к появлению касательных сил на границе между слоями. Силы, которые оказывают воздействие на границе жидкости и твердого тела, а также силы между соседними слоями жидкости всегда направлены по нормали к границе – это силы давления. Аналогично можно сказать и о газообразной среде.

Таким образом, появление поперечных волн невозможно в жидкой или газообразной средах.

В приведенном выражении k = ω υ – так называемое волновое число, а ω = 2 π f является круговой частотой.

Бегущая волна

Из указанного выражения следует:

Из вышесказанного можно сделать вывод, что, когда бегущая волна получает распространение, появляется поток энергии, пропорциональный скорости волны и квадрату ее амплитуды.

Скорость распространения волны

Бегущие волны движутся в среде с определенными скоростями, находящимися в зависимости от типа волны, инертных и упругих свойств среды.

Скорость, с которой поперечные волны распространяются в натянутой струне или резиновом жгуте, имеет зависимость от погонной массы μ (или массы единицы длины) и силы натяжения T :

Таким образом, скорость распространения продольных волн в безграничной среде, определяется по формуле:

Если речь идет о продольных волнах, получающих распространение в упругих стержнях, запись формулы для скорости волны содержит не модуль всестороннего сжатия, а модуль Юнга:

Для стали отличие E от B незначительно, а вот для прочих материалов оно может составлять 20 – 30 % и больше.

Стоячая волна

Предположим, что механическая волна, получившая распространение в некоторой среде, встретила на пути некое препятствие: в этом случае характер ее поведения резко изменится. К примеру, на границе раздела двух сред с различающимися механическими свойствами волна частично отразится, а частично проникнет во вторую среду. Волна, пробегающая по резиновому жгуту или струне, отразится от зафиксированного конца, и возникнет встречная волна. Если у струны зафиксированы оба конца, появятся сложные колебания, являющиеся итогом наложения (суперпозиции) двух волн, получающих распространение в противоположных направлениях и испытывающих отражения и переотражения на концах. Так «работают» струны всех струнных музыкальных инструментов, зафиксированные с обоих концов. Схожий процесс возникает при звучании духовых инструментов, в частности, органных труб.

Если волны, распространяющиеся по струне во встречных направлениях, обладают синусоидальной формой, то при определенных условиях они образуют стоячую волну.

По струне одновременно пробегают в противоположных направлениях две волны с одинаковой частотой:

Приведенное выражение является описанием стоячей волны. Введем некоторые понятия, применимые к такому явлению как стоячая волна.

Узлы – точки неподвижности в стоячей волне.

Пучности – точки, расположенные между узлами и колеблющиеся с максимальной амплитудой.

Набору значений λ n длин волн соответствует набор возможных частот f

В этой записи υ = T μ есть скорость, с которой распространяются поперечные волны по струне.

Согласно принципу суперпозиции стоячие волны различных видов (с разными значениями n ) способны одновременно присутствовать в колебаниях струны.

Источник

Физика. 11 класс

Конспект урока

Урок 02. Механические волны.

Перечень вопросов, рассматриваемых на уроке:

1) Механическая волна; поперечная волна; продольная волна;

2) скорость волны; длина волны;

3) звуковая волна; громкость звука; высота тона; тембр;

4) отражение; преломление; поглощение; интерференция; дифракция;

5) поляризация механических волн; когерентные источники.

Механическая волна – возмущение, распространяющееся в пространстве с течением времени.

Волновая поверхность — волна, фронт которой имеет форму плоскости.

Фронт волны — это поверхность, до которой дошли колебания к данному моменту времени.

Дифракция — явление огибания волнами препятствий.

Когерентные источники – такие источники, которые обеспечивают постоянную во времени разность фаз слагаемых волн в различных точках.

Основная и дополнительная литература по теме урока:

Мякишев Г.Я., Буховцев Б.Б., Чаругин В.М. Физика.11 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2014.С.53-66

Основное содержание урока

Механическая волна переносит энергию, но не переносит вещество.

Волны, в которых частицы среды во время колебаний сдвигаются в направлении, перпендикулярном направлению распространения волны, называются поперечными.

Волны, в которых частицы среды во время колебаний сдвигаются вдоль направления распространения волны, называются продольными.

Продольные волны могут распространяться в любой среде.

Частоту колебаний каждой точки среды называют частотой волны .

Величину, обратную частоте, называют периодом волны:

Длина волны это расстояние между двумя ближайшими точками, которые колеблются в одной фазе.

Расстояние, на которое распространяются колебания за время одного периода, называется длиной волны.

скорость волны для определенной среды

Эту формулу называют формулой волны.

Механические колебания с частотой от17 до 20 000 Гц называются звуковыми.

Разбор тренировочных заданий

1. Какой из признаков колебательного движения назван ошибочно?

1) возникает благодаря действию на тело, выведенного из положения равновесия, возвращающей силы;

2) тело движется около положения равновесия;

3) энергия в пространстве не переносится, происходит переход кинетической энергии в потенциальную и наоборот;

4) распространяется в пространстве с течением времени

Так как колебательное движение – это движение, повторяющееся через определенный промежуток времени, и тело движется около положения равновесия, и распространяется в пространстве с течением времени, то неправильным является третье утверждение: энергия в пространстве не переносится, происходит переход кинетической энергии в потенциальную и наоборот.

Правильный ответ: 3) энергия в пространстве не переносится, происходит переход кинетической энергии в потенциальную и наоборот.

2. Ультразвуковой сигнал с частотой 60кГц возвратился после отражения от дна моря на глубине 150 м через 0,2с. Длина ультразвуковой волны ________ м.

Решение: Длина волны рассчитывается по формуле:

Источник

Упругие волны (механические волны).

Возмущения, распространяющиеся в пространстве, удаляясь от места их возникновения, называют волнами.

Упругие волны — это возмущения, распространяющиеся в твердой, жидкой и газообразной средах благодаря действию в них сил упругости.

Сами эти среды называют упругими. Возмущение упругой среды — это любое отклонение частиц этой среды от своего положения равновесия.

Возьмем, например, длинную веревку (или резиновую трубку) и прикрепим один из ее концов к стене. Туго натянув веревку, резким боковым движением руки создадим на ее незакрепленном конце кратковременное возмущение. Мы увидим, что это возмущение побежит вдоль веревки и, дойдя до стены, отразится назад.

Начальное возмущение среды, приводящее к появлению в ней волны, вызывается действием в ней какого-нибудь инородного тела, которое называют источником волны. Это может быть рука человека, ударившего по веревке, камешек, упавший в воду, и т. д. Если действие источника носит кратковременный характер, то в среде возникает так называемая одиночная волна. Если же источник волны совершает длительное колебательное движение, то волны в среде начинают идти одна за другой. Подобную картину можно увидеть, поместив над ванной с водой вибрирующую пластину, имеющую наконечник, опущенный в воду.

Необходимым условием возникновения упругой волны является появление в момент возникновения возмущения сил упругости, препятствующих этому возмущению. Эти силы стремятся сблизить соседние частицы среды, если они расходятся, и отдалить их, когда они сближаются. Действуя на все более удаленные от источника частицы среды, силы упругости начинают выводить их из положения равновесия. Постепенно все частицы среды одна за другой вовлекаются в колебательное движение. Распространение этих колебаний и проявляется в виде волны.

В любой упругой среде одновременно существуют два вида движения: колебания частиц среды и распространение возмущения. Волна, в которой частицы среды колеблются вдоль направления ее распространения, называется продольной, а волна, в которой частицы среды колеблются поперек направления ее распространения, называется поперечной.

Продольная волна.

Волна, в которой колебания происходят вдоль направления распространения волны, называется продольной.

В упругой продольной волне возмущения представляют собой сжатия и разрежения среды. Деформация сжатия сопровождается возникновением сил упругости в любой среде. Поэтому продольные волны могут распространяться во всех средах (и в жидких, и в твердых, и в газообразных).

Пример распространения продольной упругой волны изображен на рисунке а и б выше. По левому концу длинной пружины, подвешенной на нитях, ударяют рукой. От удара несколько витков сближа­ются, возникает сила упругости, под действием которой эти витки начинают расходиться. Про­должая движение по инерции, они будут продолжать расходиться, минуя положение равновесия и образуя в этом месте разрежение (рисунок б). При ритмичном воздействии витки на конце пружины будут то сближаться, то отходить друг от друга, т. е. колебаться возле своего положе­ния равновесия. Эти колебания постепенно передадутся от витка к витку вдоль всей пружины. По пружине распространятся сгущения и разрежения витков, или упругая волна.

Волны, в которых колебания происходят перпендикулярно направлению их распространения, называются поперечными. В поперечной упругой волне возмущения представляют собой смещения (сдвиги) одних слоев среды относительно других.

Деформация сдвига приводит к появлению сил упругости только в твердых телах: сдвиг слоев в газах и жидкостях возникновением сил упругости не сопровождается. Поэтому поперечные волны могут распространяться только в твердых телах.

Плоская волна — это волна, у которой направление распространения одинаково во всех точках пространства.

В такой волне амплитуда не меняется со временем (по мере удаления от источника). Получить такую волну можно, если большую пластину, находящуюся в сплошной однородной упругой среде, заставить колебаться перпендикулярно плоскости. Тогда все точки среды, примыкающей к пластине, будут колебаться с одинаковыми амплитудами и одинаковыми фазами. Распространяться эти колебания будут в виде воли в направлении нормали к пластине, причем все частицы среды, лежащие в плоскостях, параллельных пластине, будут колебаться с одина­ковыми фазами.

Геометрическое место точек, в которых фаза колебаний имеет одно и то же значение, называ­ется волновой поверхностью, или фронтом волны.

С этой точки зрения плоской волне можно дать и следующее определение:

Волна называется плоской, если ее волновые поверхности представляют совокупность плоскостей, параллельных друг другу.

Линия, нормальная к волновой поверхности, называется лучом. Вдоль лучей происходит перенос энергии волны. Для плоских волн лучи — это параллельные прямые.

Уравнение плоской синусоидальной волны имеет вид:

где s — смещение колеблющейся точки, s_m — амплитуда колебаний, ω — циклическая частота, t — время, х — текущая координата, v — скорость распространения колебаний или скорость волны, φ₀ — начальная фаза колебаний.

Сферической называется волна, волновые поверхности которой имеют вид концентрических сфер. Центр этих сфер называется центром волны.

Лучи в такой волне направлены вдоль радиусов, расходящихся от центра волны. На рисунке источником волны является пульсирующая сфера.

Амплитуда колебаний частиц в сферической волне обязательно убывает по мере удаления от источника. Энергия, излучаемая источником, равномерно распределяется по поверхности сферы, радиус которой непрерывно увеличивается по мере распространения волны. Уравнение сферической волны имеет вид:

.

Источник

Механические волны.

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: механические волны, длина волны, звук.

Наличие у среды упругих свойств является необходимым условием распространения волн: деформация, возникающая в каком-либо месте, благодаря взаимодействию соседних частиц последовательно передаётся от одной точки среды к другой. Различным типам деформаций будут соответствовать разные типы волн.

Продольные и поперечные волны.

Волна называется продольной, если частицы среды колеблются параллельно направлению распространения волны. Продольная волна состоит из чередующихся деформаций растяжения и сжатия. На рис. 1 показана продольная волна, представляющая собой колебания плоских слоёв среды; направление, вдоль которого колеблются слои, совпадает с направлением распространения волны (т. е. перпендикулярно слоям).

Рис. 1. Продольная волна

Волна называется поперечной, если частицы среды колеблются перпендикулярно направлению распространения волны. Поперечная волна вызывается деформациями сдвига одного слоя среды относительно другого. На рис. 2 каждый слой колеблется вдоль самого себя, а волна идёт перпендикулярно слоям.

Рис. 2. Поперечная волна

Продольные волны могут распространяться в твёрдых телах, жидкостях и газах: во всех этих средах возникает упругая реакция на сжатие, в результате которой появятся бегущие друг за другом сжатия и разрежения среды.

Однако жидкости и газы, в отличие от твёрдых тел, не обладают упругостью по отношению к сдвигу слоёв. Поэтому поперечные волны могут распространяться в твёрдых телах, но не внутри жидкостей и газов*.

Важно отметить, что частицы среды при прохождении волны совершают колебания вблизи неизменных положений равновесия, т. е. в среднем остаются на своих местах. Волна, таким образом, осуществляет
перенос энергии, не сопровождающийся переносом вещества.

Наиболее просты для изучения гармонические волны. Они вызываются внешним воздействием на среду, меняющимся по гармоническому закону. При распространении гармонической волны частицы среды совершают гармонические колебания с частотой, равной частоте внешнего воздействия. Гармоническими волнами мы в дальнейшем и ограничимся.

Скоростью распространения волны называется отношение длины волны к периоду колебаний частиц среды:

Частотой волны называется частота колебаний частиц:

Отсюда получаем связь скорости волны, длины волны и частоты:

Тон — это звук, который издаёт тело, совершающее гармонические колебания (например, камертон или струна). Высота тона определяется частотой этих колебаний: чем выше частота, тем выше нам кажется звук. Так, натягивая струну, мы увеличиваем частоту её колебаний и, соответственно, высоту звука.

Источник

Механические волны

Если в каком-нибудь месте твердой, жидкой или газообразной среды возбуждены колебания частиц, то вследствие взаимодействия атомов и молекул среды колебания начинают передаваться от одной точки к другой с конечной скоростью. Процесс распространения колебаний в среде называется волной.

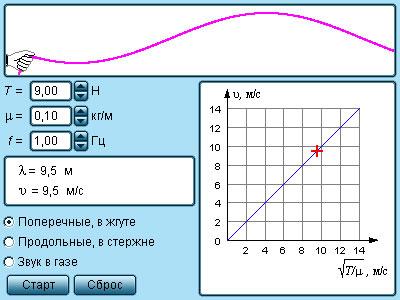
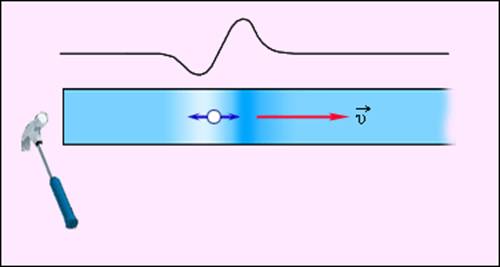
Механические волны бывают разных видов. Если в волне частицы среды испытывают смещение в направлении, перпендикулярном направлению распространения, то волна называется поперечной. Примером волны такого рода могут служить волны, бегущие по натянутому резиновому жгуту (рис. 2.6.1) или по струне.

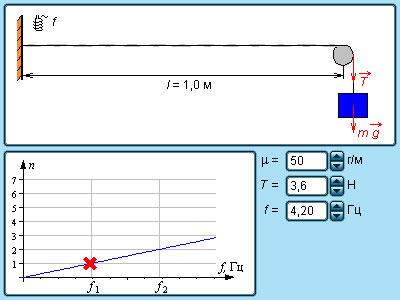
Если смещение частиц среды происходит в направлении распространения волны, то волна называется продольной. Волны в упругом стержне (рис. 2.6.2) или звуковые волны в газе являются примерами таких волн.

Волны на поверхности жидкости имеют как поперечную, так и продольную компоненты.

Как в поперечных, так и в продольных волнах переноса вещества в направлении распространения волны не происходит. В процессе распространения частицы среды лишь совершают колебания около положений равновесия. Однако волны переносят энергию колебаний от одной точки среды к другой.

Распространение поперечного волнового импульса по натянутому резиновому жгуту

Распространение продольного волнового импульса по упругому стержню

Характерной особенностью механических волн является то, что они распространяются в материальных средах (твердых, жидких или газообразных). Существуют волны, которые способны распространяться и в пустоте (например, световые волны). Для механических волн обязательно нужна среда, обладающая способностью запасать кинетическую и потенциальную энергию. Следовательно, среда должна обладать инертными и упругими свойствами. В реальных средах эти свойства распределены по всему объему. Так, например, любой малый элемент твердого тела обладает массой и упругостью. В простейшей одномерной модели твердое тело можно представить как совокупность шариков и пружинок (рис. 2.6.3).

Простейшая одномерная модель твердого тела

В этой модели инертные и упругие свойства разделены. Шарики обладают массой m, а пружинки – жесткостью k. С помощью такой простой модели можно описать распространение продольных и поперечных волн в твердом теле. В продольных волнах шарики испытывают смещения вдоль цепочки, а пружинки растягиваются или сжимаются. Такая деформация называется деформацией растяжения или сжатия. В жидкостях или газах деформация такого рода сопровождается уплотнением или разрежением.

Продольные механические волны могут распространяться в любых средах – твердых, жидких и газообразных.

Продольные волны – это периодические сгущения и разрежения среды. Поэтому такие волны могут существовать в любых телах – твердых, жидких, газообразных. Поперечные волны могут существовать лишь в твердых телах. Это объясняется тем, что для распространения такой волны необходимо «жесткое» расположение частиц среды, чтобы между ними могли возникать силы упругости.

Если в одномерной модели твердого тела один или несколько шариков сместить в направлении, перпендикулярном цепочке, то возникнет деформация сдвига. Деформированные при таком смещении пружины будут стремиться возвратить смещенные частицы в положение равновесия. При этом на ближайшие несмещенные частицы будут действовать упругие силы, стремящиеся отклонить их от положения равновесия. В результате вдоль цепочки побежит поперечная волна.

В жидкостях и газах упругая деформация сдвига не возникает. Если один слой жидкости или газа сместить на некоторое расстояние относительно соседнего слоя, то никаких касательных сил на границе между слоями не появится. Силы, действующие на границе жидкости и твердого тела, а также силы между соседними слоями жидкости всегда направлены по нормали к границе – это силы давления. То же относится к газообразной среде. Следовательно, поперечные волны не могут существовать в жидкой или газообразной средах.

Значительный интерес для практики представляют простые гармонические или синусоидальные волны. Они характеризуются амплитудой A колебания частиц, частотой f и длиной волны λ. Синусоидальные волны распространяются в однородных средах с некоторой постоянной скоростью υ.

Смещение y (x, t) частиц среды из положения равновесия в синусоидальной волне зависит от координаты x на оси OX, вдоль которой распространяется волна, и от времени t по закону:

– так называемое волновое число, ω = 2πf – круговая частота.

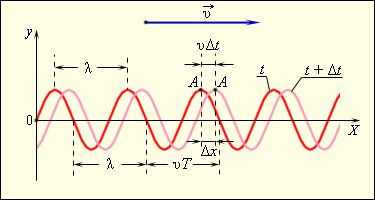
На рис. 2.6.4 изображены «моментальные фотографии» поперечной волны в два момента времени: t и t + Δt. За время Δt волна переместилась вдоль оси OX на расстояние υΔt. Такие волны принято называть бегущими (в отличие от стоячих волн, см. далее).

«Моментальные фотографии» бегущей синусоидальной волны в момент времени t и t + Δt

Длиной волны λ называют расстояние между двумя соседними точками на оси OX, колеблющимися в одинаковых фазах. Расстояние, равное длине волны λ, волна пробегает за период Т, следовательно, λ = υT, где υ – скорость распространения волны.

Для любой выбранной точки на графике волнового процесса (например, для точки A на рис. 2.6.4) с течением времени t изменяется координата x этой точки, а значение выражения ωt – kx не изменяется. Через промежуток времени Δt точка A переместится по оси OX на некоторое расстояние Δx = υΔt. Следовательно:

Таким образом, бегущая синусоидальная волна обладает двойной периодичностью – во времени и пространстве. Временной период равен периоду колебаний T частиц среды, пространственный период равен длине волны λ. Волновое число является пространственным аналогом круговой частоты

Обратим внимание на то, что уравнение

описывает синусоидальную волну, распространяющуюся в направлении, противоположном направлению оси OX, со скоростью .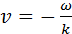

В бегущей синусоидальной волне каждая частица среды совершает гармонические колебания с некоторой частотой ω. Поэтому, как и в случае простого колебательного процесса, средняя потенциальная энергия, запасенная в некотором объеме среды, равна средней кинетической энергии в том же объеме и пропорциональна квадрату амплитуды колебаний.

Отсюда следует, что при распространении бегущей волны возникает поток энергии, пропорциональный скорости волны и квадрату ее амплитуды.

Бегущие волны распространяются в средах с определенными скоростями, зависящими от типа волны, а также от инертных и упругих свойств среды.

Скорость поперечных волн в натянутой струне или резиновом жгуте зависит от погонной массы μ (т. е. массы единицы длины) и силы натяжения T:

Скорость распространения продольных волн в безграничной среде определяется плотностью среды ρ (т. е. массой единицы объема) и модулем всестороннего сжатия B, который равен коэффициенту пропорциональности между изменением давления Δp и относительным изменением объема ΔV / V, взятому с обратным знаком:

Выражение для скорости распространения продольных волн в безграничных средах имеет вид

Например, при температуре 20 °С скорость распространения продольных волн в воде υ ≈ 1480 м/с, в различных сортах стали υ ≈ 5–6 км/с.

При распространении продольных волн в упругих стержнях в формулу для скорости волн вместо модуля всестороннего сжатия B входит модуль Юнга E :

Для стали отличие E от B невелико, для других материалов оно может составлять 20–30 % и даже больше.

Если механическая волна, распространяющаяся в среде, встречает на своем пути какое-либо препятствие, то она может резко изменить характер своего поведения. Например, на границе раздела двух сред с разными механическими свойствами волна частично отражается, а частично проникает во вторую среду. Волна, бегущая по резиновому жгуту или струне отражается от неподвижно закрепленного конца; при этом появляется волна, бегущая во встречном направлении. В струне, закрепленной на обоих концах, возникают сложные колебания, которые можно рассматривать как результат наложения (суперпозиции) двух волн, распространяющихся в противоположных направлениях и испытывающих отражения и переотражения на концах. Колебания струн, закрепленных на обоих концах, создают звуки всех струнных музыкальных инструментов. Очень похожее явление возникает при звучании духовых инструментов, в том числе органных труб.

Если волны, бегущие по струне во встречных направлениях, имеют синусоидальную форму, то при определенных условиях они могут образовать стоячую волну.

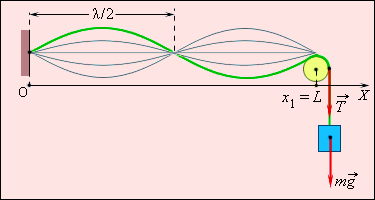
Пусть струна длины l закреплена так, что один из ее концов находится в точке x = 0, а другой – в точке x₁ = L (рис. 2.6.5). В струне создано натяжение T.

Образование стоячей волны в струне, закрепленной на обоих концах

По струне одновременно распространяются в противоположных направлениях две волны одной и той же частоты:

В точке x = 0 (один из закрепленных концов струны) падающая волна y₁ в результате отражения порождает волну y₂. При отражении от неподвижно закрепленного конца отраженная волна оказывается в противофазе с падающей. Согласно принципу суперпозиции, который является экспериментальным фактом, колебания, вызванные встречными волнами в каждой точке струны, складываются. Таким образом, результирующее колебание в каждой точке равно сумме колебаний, вызванных волнами y₁ и y₂ в отдельности. Следовательно,

Это и есть стоячая волна. В стоячей волне существуют неподвижные точки, которые называются узлами. Посередине между узлами находятся точки, которые колеблются с максимальной амплитудой. Эти точки называются пучностями.

Оба неподвижных конца струны должны быть узлами. Приведенная выше формула удовлетворяет этому условию на левом конце (x = 0). Для выполнения этого условия и на правом конце (x = L), необходимо чтобы kL = nπ, где n – любое целое число. Это означает, что стоячая волна в струне возникает не всегда, а только в том случае, если длина L струны равняется целому числу длин полуволн:

Набору значений λn длин волн соответствует набор возможных частот fn:

где – скорость распространения поперечных волн по струне. Каждая из частот и связанный с ней тип колебания струны называется нормальной модой. Наименьшая частота f₁ называется основной частотой, все остальные (f₂, f₃, …) называются гармониками. На рис. 2.6.5 изображена нормальная мода для n = 2.

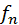
В стоячей волне нет потока энергии. Колебательная энергия, заключенная в отрезке струны между двумя соседними узлами, не транспортируется в другие части струны. В каждом таком отрезке происходит периодическое (дважды за период T) превращение кинетической энергии в потенциальную и обратно как в обычной колебательной системе. Но в отличие от груза на пружине или маятника, у которых имеется единственная собственная частота

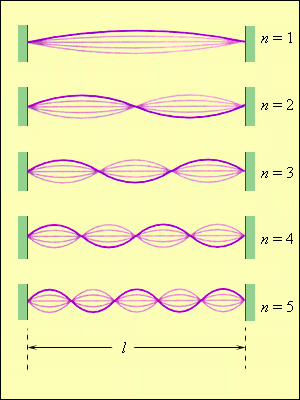
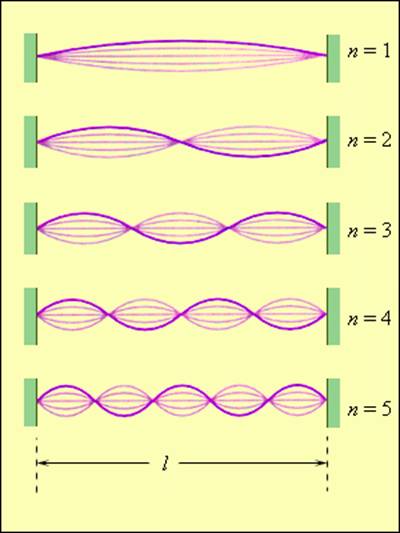
струна обладает бесконечным числом собственных (резонансных) частот fn. На рис. 2.6.6 изображены несколько типов стоячих волн в струне, закрепленной на обоих концах.

Первые пять нормальных мод колебаний струны, закрепленной на обоих концах

В соответствии с принципом суперпозиции стоячие волны различных типов (т. е. с разными значениями n) могут одновременно присутствовать в колебаниях струны.

Источник