Что такое медиана четырехугольника

Параллелограмм: свойства и признаки

Определение параллелограмма

Параллелограмм — это четырехугольник, у которого противоположные стороны попарно параллельны и равны. Как выглядит параллелограмм:

Частные случаи параллелограмма: ромб, прямоугольник, квадрат.

Диагонали — отрезки, которые соединяют противоположные вершины.

Свойства диагоналей параллелограмма:

Биссектриса угла параллелограмма — это отрезок, который соединяет вершину с точкой на одной из двух противоположных сторон и делит угол при вершине пополам.

Свойства биссектрисы параллелограмма:

Как найти площадь параллелограмма:

Периметр параллелограмма — сумма длины и ширины, умноженная на два.

P = 2 × (a + b), где a — ширина, b — высота.

У нас есть отличные дополнительные курсы по математике для учеников с 1 по 11 классы!

Свойства параллелограмма

Геометрическая фигура — это любое множество точек. У каждой фигуры есть свои свойства, которые отличают их между собой и помогают решать задачи по геометрии в 8 классе.

Рассмотрим основные свойства диагоналей и углов параллелограмма, узнаем чему равна сумма углов параллелограмма и другие особенности этой фигуры. Вот они:

А сейчас докажем теорему, которая основана на первых двух свойствах.

Теорема 1. В параллелограмме противоположные стороны и противоположные углы равны.

В любом выпуклом четырехугольнике диагонали пересекаются. Все, что мы знаем о точке их пересечения — это то, что она лежит внутри четырехугольника.

Если мы проведем обе диагонали в параллелограмме, точка пересечения разделит их пополам. Убедимся, так ли это:

Теорема доказана. Наше предположение верно.

Признаки параллелограмма

Признаки параллелограмма помогают распознать эту фигуру среди других четырехугольников. Сформулируем три основных признака.

Первый признак параллелограмма. Если в четырехугольнике две противолежащие стороны равны и параллельны, то этот четырехугольник — параллелограмм.

Докажем 1 признак параллелограмма:

Шаг 1. Пусть в четырехугольнике ABCD:

Чтобы назвать этот четырехугольник параллелограммом, нужно внимательно рассмотреть его стороны.

Сейчас мы видим одну пару параллельных сторон. Нужно доказать, что вторая пара сторон тоже параллельна.

Шаг 2. Проведем диагональ. Получились два треугольника ABC и CDA, которые равны по первому признаку равенства, то есть по по двум сторонам и углу между ними:

Шаг 3. Из равенства треугольников также следует:

Эти углы тоже являются внутренними накрест лежащими для прямых CB и AD. А это как раз и есть признак параллельности прямых. Значит, CB || AD и ABCD — параллелограмм.

Вот так быстро мы доказали первый признак.

Второй признак параллелограмма. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник — параллелограмм.

Докажем 2 признак параллелограмма:

Шаг 1. Пусть в четырехугольнике ABCD:

Шаг 2. Проведем диагональ AC и рассмотрим треугольники ABC и CDA:

Из этого следует, что треугольники ABC и CDA равны по третьему признаку, а именно по трем сторонам.

Шаг 3. Из равенства треугольников следует:

А так как эти углы — накрест лежащие при сторонах BC и AD и диагонали AC, значит, стороны BC и AD параллельны.

Эти углы — накрест лежащие при сторонах AB и CD и секущей AC. Поэтому стороны AB и CD тоже параллельны. Значит, четырехугольник ABCD — параллелограмм, ЧТД.

Доказали второй признак.

Третий признак параллелограмма. Если в четырехугольнике диагонали точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм.

Докажем 3 признак параллелограмма:

Шаг 1. Если диагонали четырехугольника ABCD делятся пополам точкой O, то треугольник AOB равен треугольнику COD по двум сторонам и углу между ними:

Шаг 2. Из равенства треугольников следует, что CD = AB.

Эти стороны параллельны CD || AB, по равенству накрест лежащих углов: ∠1 = ∠2 (следует из равенства треугольников AOB и COD).

Значит, ABCD является параллелограммом по первому признаку, который мы доказали ранее. Что и требовалось доказать.

Теперь мы знаем свойства параллелограмма и то, что выделяет его среди других четырехугольников — признаки. Так как они совпадают, эти формулировки можно использовать для определения параллелограмма. Но самое распространенное определение все-таки связано с параллельностью противоположных сторон.

Источник

Медиана (геометрия)

Медиана треугольника ― отрезок внутри треугольника, соединяющий вершину треугольника с серединой противоположной стороны, а также прямая, содержащая этот отрезок.

Содержание

Свойства

Формулы

Мнемоническое правило

Медиана — это обезьяна, лазает по сторонам, делит их напополам.

См. также

Ссылки

Полезное

Смотреть что такое «Медиана (геометрия)» в других словарях:

Медиана треугольника — У этого термина существуют и другие значения, см. Медиана. Треугольник и его медианы. Медиана треугольника (лат. … Википедия

Треугольник — У этого термина существуют и другие значения, см. Треугольник (значения). Треугольник (в евклидовом пространстве) это геометрическая фигура, образованная тремя отрезками, которые соединяют три не лежащие на одной прямой точки. Три точки,… … Википедия

Клейн, Феликс — Феликс Клейн Дата рождения: 25 апреля 1849(1849 04 25 … Википедия

Клейн Ф. — Феликс Клейн Дата рождения: 25 апреля, 1849 Место рождения: Дюссельдорф, Германия Дата смерти: 22 июня, 1925 Место смерти: Гёттинген Гражданство … Википедия

Клейн Феликс — Феликс Клейн Дата рождения: 25 апреля, 1849 Место рождения: Дюссельдорф, Германия Дата смерти: 22 июня, 1925 Место смерти: Гёттинген Гражданство … Википедия

Феликс Клейн — Дата рождения: 25 апреля, 1849 Место рождения: Дюссельдорф, Германия Дата смерти: 22 июня, 1925 Место смерти: Гёттинген Гражданство … Википедия

Эрлангенская программа — Феликс Клейн Эрлангенская программа выступление 23 летнего немецкого математика Феликса Клейна в Эрлангенском университете (октябр … Википедия

Математическая статистика — Математическая статистика наука, разрабатывающая математические методы систематизации и использования статистических данных для научных и практических выводов. Во многих своих разделах математическая статистика опирается на … Википедия

Прямоугольный треугольник — Прямоугольный треугольник это треугольник, в котором один угол прямой (то есть составляет 90 градусов). Соотношения между сторонами и … Википедия

Теорема Аполлония — Зелёное + Голубое = Красное В планиметрии теорема Аполлония является формулой, выражающей длину медианы треугольника через … Википедия

Источник

Медиана треугольника. Теоремы связанные с медианами треугольника. Формулы для нахождения медиан

Медиана треугольника — это отрезок, соединяющий верщину треугольника с серединой противолежащей стороны этого треугольника.

Свойства медиан треугольника

1. Медиана разбивает треугольник на два треугольника одинаковой площади.

2. Медианы треугольника пересекаются в одной точке, которая делит каждую из них в отношении 2:1, считая от вершины. Эта точка называется центром тяжести треугольника (центроидом).

3. Весь треугольник разделяется своими медианами на шесть равновеликих треугольников.

Длина медианы проведенной к стороне: (док-во достроением до параллелограмма и использованием равенства в параллелограмме удвоенной суммы квадратов сторон и суммы квадратов диагоналей )

Т1. Три медианы треугольника пересекаются в одной точке М, которая делит каждую из них в отношении 2:1, считая от вершин треугольника. Дано: ∆ABC, СС₁, АА₁, ВВ₁ — медианы
∆ABC. Доказать: и

. Д-во: Пусть М — точка пересечения медиан СС₁, АА₁ треугольника ABC. Отметим A₂ — середину отрезка AM и С₂ — середину отрезка СМ. Тогда A₂C₂ — средняя линия треугольника АМС. Значит,А₂ С₂ || АС

На медиане АА₁ такой точкой является точка М, следовательно, точка М и есть точка пересечения медиан АА₁ иBB_1.

Таким образом, n

Доказать:S_AMB =S_BMC =S_AMC. Доказательство. и высота, проведенная из вершины В, у них общая. т.к. равны их основания и высота, проведенная из вершины М, у них общая. Тогда

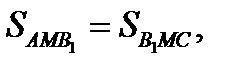
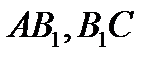
Биссектриса треугольника.Теоремы связанные с биссектрисами треугольника. Формулы для нахождения биссектрис

Биссектриса угла — луч с началом в вершине угла, делящий угол на два равных угла.

Биссектриса угла есть геометрическое место точек внутри угла, равноудалённых от сторон угла.

1. Теорема о биссектрисе: Биссектриса внутреннего угла треугольника делит противоположную сторону в отношении, равном отношению двух прилежащих сторон

2. Биссектрисы внутренних углов треугольника пересекаются в одной точке — инцентре — центре вписанной в этот треугольник окружности.

3. Если в треугольнике две биссектрисы равны, то треугольник — равнобедренный (теорема Штейнера — Лемуса).

Вычисление длины биссектрисы

l_c — длина биссектрисы, проведённой к стороне c,

a,b,c — стороны треугольника против вершин A,B,C соответственно,

p — полупериметр треугольника,

a_l,b_l — длины отрезков, на которые биссектриса l_c делит сторону c,

α,β,γ — внутренние углы треугольника при вершинах A,B,C соответственно,

h_c — высота треугольника, опущенная на сторону c.

Метод площадей.

Характеристика метода. Из названия следует, что главным объектом данного метода является площадь. Для ряда фигур, например для треугольника, площадь довольно просто выражается через разнообразные комбинации элементов фигуры (треугольника). Поэтому весьма эффективным оказывается прием, когда сравниваются различные выражения для площади данной фигуры. В этом случае возникает уравнение, содержащее известные и искомые элементы фигуры, разрешая которое мы определяем неизвестное. Здесь и проявляется основная особенность метода площадей – из геометрической задачи он «делает» алгебраическую, сводя все к решению уравнения (а иногда системы уравнений).

Можно выделить 2 направления этого метода:

1) Метод сравнения: связан с большим кол-вом формул S одних и тех же фигур

2) Метод отношения S: основан на след опорных задачах:

Теорема Чевы

Доказательство.

Обозначим через точку пересечения отрезков и . Опустим из точек С и А перпендикуляры на прямую ВВ₁ до пересечения с ней в точках Kи L соответственно (см. рисунок).

Поскольку треугольники и имеют общую сторону , то их площади относятся как высоты, проведенные на эту сторону, т.е. AL иCK :

Последнее равенство справедливо, так как прямоугольные треугольники 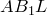и подобны по острому углу.

Аналогично получаем и

Перемножим эти три равенства:

что и требовалось доказать.

Замечание. Отрезок (или продолжение отрезка), соединяющий вершину треугольника с точкой, лежащей на противоположной стороне или ее продолжении, называется чевианой.

Теорема (обратная теорема Чевы). Пусть точки A’,B’,C’ лежат на сторонах BC,CA и AB треугольника ABC соответственно. Пусть выполняется соотношение

Тогда отрезки AA’,BB’,CC’ и пересекаются в одной точке.

Теорема Менелая

Теорема Менелая. Пусть прямая пересекает треугольник ABC, причем C₁ – точка ее пересечения со стороной AB, A₁ – точка ее пересечения со стороной BC, и B₁ – точка ее пересечения с продолжением стороны AC. Тогда

Доказательство. Проведем через точку C прямую, параллельную AB. Обозначим через K ее точку пересечения с прямой B₁C₁.

ТреугольникиAC₁B₁иCKB₁подобны (∟C₁AB₁= ∟KCB₁, ∟AC₁B₁= ∟CKB₁). Следовательно,

Из каждого равенства выразим CK:

Откуда что и требовалось доказать.

Теорема (обратная теорема Менелая). Пусть дан треугольник ABC. Пусть точка C₁ лежит на стороне AB, точка A₁ – на стороне BC, а точка B₁ – на продолжении стороны AC, причем выполняется соотношение

Тогда точки A₁,B₁ и C₁ лежат на одной прямой.

Дата добавления: 2018-05-13 ; просмотров: 6931 ; Мы поможем в написании вашей работы!

Источник

Определение и свойства медианы в равнобедренном треугольнике

В данной статье мы рассмотрим определение и свойства медиан, проведенных к основанию и боковым сторонам равнобедренного треугольника, а также разберем пример решения задачи для закрепления теоретического материала.

Определение медианы

Медианой называется отрезок в треугольнике, который соединяет вершину и середину противоположной стороны.

Треугольник является равнобедренным, если две его стороны равны (боковые), а третья сторона – это основание фигуры.

Свойства медианы в равнобедренном треугольнике

Свойство 1

Медиана в равнобедренном треугольнике, проведенная к основанию, одновременно является высотой, опущенной на основание, и биссектрисой угла, из которого она проведена.

Свойство 2

В равнобедренном треугольнике медианы пресекаются в одной точке (центр тяжести) и делятся в этой точке в отношении 2:1.

Свойство 3

Медиана делит равнобедренный треугольник на 2 равных по площади (равновеликих) треугольника. Следовательно, S₁ = S₂.

Свойство 4

Если провести три медианы в равнобедренном треугольнике, образуются 6 равновеликих треугольников (S₁ = S₂ = S₃ = S₄ = S₅ = S₆).

Свойство 5

Длину медианы в равнобедренном треугольнике, проведенную к основанию, можно найти по следующей формуле:

Свойство 6

Данной свойство, в отличие от перечисленных выше, не относится к медиане, опущенной на основание фигуры. Оно гласит:

Медианы, проведенные к боковым сторонам равнобедренного треугольника, равны между собой.

AF = CE, следовательно, AE = EB = BF = FC.

Пример задачи

Основание равнобедренного треугольника равняется 7 см, а боковая сторона – 12 см. Найдите длину медианы, проведенной к основанию фигуры.

Решение
Воспользуемся формулой, представленной в Свойстве 5, подставив в нее известные нам по условиям задачи значения:

Источник

Свойства медианы треугольника. Итоговое повторение курса геометрии 7 – 9 класса

Свойства медианы треугольника

Итоговое повторение курса геометрии 7 – 9 класса

При изучении какой-либо темы школьного курса можно отобрать определенный минимум задач, овладев методами решения которых, учащиеся будут в состоянии решить любую задачу на уровне программных требований по изучаемой теме. Предлагаю рассмотреть задачи, которые позволят увидеть взаимосвязи отдельных тем школьного курса математики. Поэтому составленная система задач является эффективным средством повторения, обобщения и систематизации учебного материала в ходе подготовки учащихся к экзамену.

Для сдачи экзамена не лишними будут дополнительные сведения о некоторых элементах треугольника. Рассмотрим свойства медианы треугольника и задачи, при решении которых этими свойствами можно воспользоваться. В предложенных задачах реализуется принцип уровневой дифференциации. Все задачи условно поделены на уровни (уровень указан в скобках после каждого задания).

Вспомним некоторые свойства медианы треугольника

Свойство 1. Докажите, что медиана треугольника ABC, проведённая из вершины A, меньше полусуммы сторон AB и AC.

Отложим на продолжении медианы AM за точку M отрезок MK, равный AM. Тогда в четырёхугольнике ABKC диагонали пересекаются и точкой пересечения делятся пополам. Значит, ABKC — параллелограмм. Применяя неравенство треугольника к треугольнику ABK, получим, что

то, сложив почленно эти три неравенства, получим, что

2AM + BN + CK > AB + BC + AC.

Отсюда следует, что AM + BN + CK > (AB + BC + AC).

Отложим на продолжении медианы AM за точку M отрезок MA1, равный AM. Тогда ABA1C — параллелограмм. Поэтому

так расположить точки нельзя.

№32 Темы: Удвоение медианы. Ортоцентр и ортотреугольник Сложность:5 + Три точки, лежащие на одной прямой Подобные треугольники Классы: 9,10

Решение

Пусть A’B’C’ – треугольник, образованный

проведенными прямыми и G – точка пересечения его

сторонам треугольника A’B’C’ соответственно, поэтому эти треугольники подобны, причем соответствующие прямые BC и

Источник: Всероссийская олимпиада по математике, 2008 г, 9 класс

Отрабатываем умение: самостоятельно решать задачи.

Свойства медианы. Площадь треугольника

1. В треугольнике АВС медиана АМ перпендикулярна медиане BN. Найдите площадь треугольника АВС, если длина АМ равна 3, а длина BN равна 4.

2. Основание равнобедренного треугольника равно 2. Медианы, проведенные к боковым сторонам, взаимно перпендикулярны. Найдите площадь треугольника.

3. Две медианы равнобедренного треугольника взаимно перпендикулярны. Боковая сторона равна . Найдите площадь треугольника.

4. В треугольнике АВС медианы АD и ВE перпендикулярны, , . Чему равен квадрат третьей стороны?

5. Сторона треугольника равна 20, а медианы, проведенные к двум другим сторонам – 24 и 18. Найдите площадь треугольника.

6. Стороны треугольника равны 13, 14 и 15. Найти площади треугольников, на которые разбивается данный треугольник его медианами.

7. Площадь треугольника АВС равна 12. Из вершины тупого угла В проведена медиана BD, длина которой равна 3. Найдите длину стороны АС, если угол ABD – прямой.

8. Найдите площадь треугольника, если две его стороны равны 1 и , а медиана третьей стороны равна 2. (Указание – достроить до параллелограмма).

О т в е т: .

1. Одна сторона треугольника равна а, другая – b. Найдите третью сторону, если известно, что она равна медиане, проведенной к ней.

О т в е т: .

2. Основание равнобедренного треугольника , медиана боковой стороны 5. Найдите длины боковых сторон.

3. В равнобедренном треугольнике основание равно , а угол при основании равен 300. Найдите длину медианы, проведенной к боковой стороне.

4. Медианы треугольника равны 5, и . Докажите, что треугольник прямоугольный.

5. Числа , и выражают длины медиан некоторого треугольника. Докажите, что если выполняется равенство , то треугольник является прямоугольным.

Медиана, проведенная к гипотенузе

1. Медиана, проведенная к гипотенузе прямоугольного треугольника, равна 3 см и делит прямой угол в отношении 2:1. Найдите меньший катет.

2. АА1, ВВ1, СС1 – медианы треугольника АВС. . Найдите .

3. Медианы треугольника АВС АА1, ВВ1 и СС1 пересекаются в точке О. .см. см. Найдите ВО.

4. Гипотенуза прямоугольного треугольника в 4 раза больше проведенной к ней высоты. Найдите острые углы треугольника.

5. В трапеции ABCD углы при основании AD равны 200 и 700, длина отрезка, соединяющего середины оснований, равна 3. Найдите длину отрезка, соединяющего середины диагоналей трапеции.

· интернет сайт http://zadachi. ***** Задачи по геометрии

· Всероссийская олимпиада по математике, 2008 год,

· Турнир им. Ломоносова, 2001 год

· Московская математическая регата, 2012/13 г, 8 класс

Источник