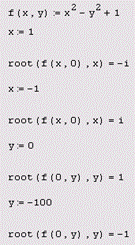Что такое маткад и для чего он нужен

Обзор Mathcad. Лучший помощник в вычислениях.

Дорогие друзья. Мы уже вели с вами беседу об опасностях, подстерегающих начинающего математика, физика и инженера. Как бы ни была интересна сама суть науки, для того, чтобы описать эту самую суть, применяется математический аппарат. И вот этот самый аппарат, со своими громоздкими выкладками, приближениями, углами тета фи и кси зачастую уничтожает в студентах всякий интерес к описываемому вопросу. В этой статье мы не будем говорить о том, как подогреть этот интерес, нет. Поговорим о том, как избежать громоздких математических выкладок.

Сразу оговоримся, мы не агитируем за то, чтобы не учиться считать вручную, как раз наоборот. Еще Михаил Васильевич Ломоносов говорил: математику уже затем учить надо, что она ум в порядок приводит. И он был совершенно прав. Кто сомневается – попробуйте!

Тем не менее, современные объемы информации таковы, что зачастую считать вручную бывает просто физически невозможно. Как быть?

Известно как! Ведь мы уже проводили обзор МАTLAB, скажете Вы. Да, все верно, но помимо матлаба, существуют и другие средства. Для общего развития, их полезно знать. Пакеты Mathcad, Maple, Mathematica, Maxima и еще множество других.

Одно из них – пакет Mathсad. Настолько простая и удобная программа, что мы просто не можем обойти ее стороной.

Изначально Mathсad создавался для решения задач не теоретической, а прикладной математики. Т.е. задач, не требующих глубокого внедрения в математическую суть проблемы, а использующих математику лишь как средство решения. Начиная с 14-й версии, в Mathсad используется символьное ядро MuPAD. При этом, в отличие от более мощной программы Maple, символьное ядро Mathсad искусственно ограничено. Тем не менее, 300 доступных функций обеспечивают возможность для решения большого количества задач инженерного характера. В помощь статья как сделать презентацию в powerpoint.

Еще одно выгодное отличие Mathсad – это интерфейс. Ввод данных является графическим, а не текстовым. Что это значит? Это значит, что Вы не набираете формулы каким-то замудренным методом, а записываете их в рабочее поле в совершенно обычном, привычном книжном виде. Используя для этого или клавиатуру, или перетаскивая значки с панелей инструментов Mathсad.

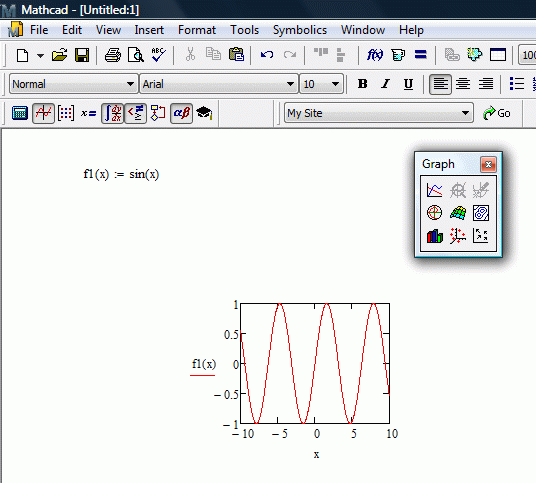
Для примера, расскажем ниже, как задать функцию в маткаде, а затем построить график функции. Пусть это будет простая функция – с простыми функциями все всегда понятнее. Скажем, f(x)=sinx

затем открываем панель Graph, нажимаем X-Y Plot, и выбираем нужный нам вид графика. Оси для удобства можно подписывать самостоятельно, также график можно растягивать и сжимать.

Рассмотрим ниже некоторые возможности маткада на примерах, в контексте самых популярных и часто используемых его функций. Надеемся, данная информация будет полезна начинающим пользователям.
Например, есть общая задача: нужно решить уравнение. Какие способы и встроенные функции предлагает для этого Mathcad? Идем по порядку.

1) Функция root (англ. Root – корень). Данная функция используется для нахождения корней уравнения с одним неизвестным. Запись в Mathcad выглядит следующим образом:

Здесь x – переменная, варьируя значение которой программа будет искать точки пересечения графика y=f(x) с осью абсцисс.

2) Функция find (англ. Find – искать, найти). Известно, что с помощью Mathcad можно решать не только уравнения, но также и уравнения с несколькими переменными, а также системы уравнений, число которых может достигать аж 50-ти. Именно в таких случаях помогает данная функция. При решении системы перед самими уравнениями слудует написать слово given, указывающее программе, что далее соедует система уравнений. Связка given-find возвращает значения переменных, обращающих уравнение в верное тождество. Для случая систем уравнений возвращается в виде вектора. Записывается в виде

А теперь, как это выглядит в рабочем поле маткада, с произвольными значениями

3) Функция minerr. Если функция find позволяет найти только точные значения, то при помощи оператора minerr Вы сможете найти приближенные значения корней уравнения и системы уравнений с равным количеством уравнений и неизвестных. Записывается так:

Minerr(x1, x2, …)

4) На случай решения систем линейных алгебраических уравнений (СЛАУ), когда необходимы операции над матрицами, Mathcad имеет встроенную функцию

Например, представим, что нам нужно решить линейную систему уравнений вида

В матричном виде данная система запишется следующим образом

B- столбец свободных членов.
Именно матрица коэффициентов и столбец свободных членов являются аргументами функции lsolve(A, B), возвращающей вектор-столбец решений СЛАУ.

Надеемся, что данная статья будет полезна начинающим пользователям Mathcad, а также тем, кто только собирается взяться за его освоение. Можно с уверенностью сказать одно: из всех подобных программ, Mathcad обладает явными преимуществами. Простота интерфейса в сочетании с широким набором возможностей делают эту программу популярной как среди зеленых студентов, так и среди состоявшихся ученых мужей мирового масштаба.

Напоследок, несколько слов о системных требованиях. Как уже говорилось, программа многофункциональна, но по мощности уступает своим аналогам. А значит, маткад будет уверенно чувствовать себя на потрепанном стареньком лэптопе. Для успешной установки Вам понадобится:

— 32-х или 64-х битный процессор с тактовой частотой 400 МГц (рекомендовано 700 МГц)

— 256 МБ ОЗУ (рекомендовано 512 Мб)

— 1,75 Гб свободного пространства на диске

— Видеокарта SVGA или выше, монитор, поддерживающий разрешение 1024×768 и выше

Удачи в учебе! И помните, ничего сверхсложного в решении, казалось бы, громоздких задач, нет. Немного усердия, немного практики, и дело пойдет на лад. В принципе, не бывает нерешаемых задач, нужен только верный подход. А если Вам нужна консультация, по любому вопросу смело обращайтесь к нашим специалистам.

Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.

Источник

Назначение и основные возможности программного пакета MathCAD.

Назначение и основные возможности программного пакета MathCAD.

Основные возможности

Mathcad содержит сотни операторов и встроенных функций операторов для решения различных технических задач. Программа позволяет выполнять численные и символьные вычисления, производить операции с скалярными величинами, векторами и матрицами, автоматически переводить одни единицы измерения в другие.

Среди возможностей Mathcad можно выделить:

— Решение дифференциальных уравнений, в том числе и численными методами

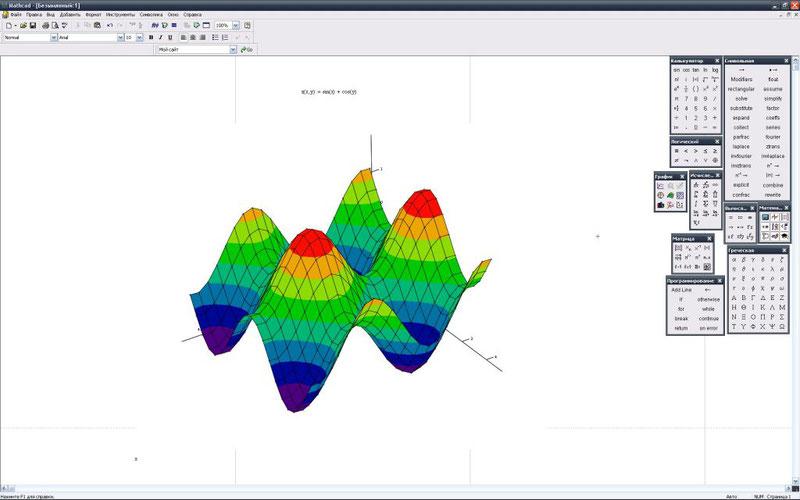
— Построение двумерных и трёхмерных графиков функций (в разных системах координат, контурные, векторные и т. д.)

— Использование греческого алфавита как в уравнениях, так и в тексте

— Выполнение вычислений в символьном режиме

— Выполнение операций с векторами и матрицами

— Символьное решение систем уравнений

— Поиск корней многочленов и функций

— Проведение статистических расчётов и работа с распределением вероятностей

— Поиск собственных чисел и векторов

— Вычисления с единицами измерения

— Интеграция с САПР системами, использование результатов вычислений в качестве управляющих параметров

— С помощью Mathcad инженеры могут документировать все вычисления в процессе их проведения.

Из чего состоит библиотека встроенных функций.

Мощная библиотека встроенных функций позволяет решать широкий круг инженерных и математических задач:

Типы данных.

Массивы в Mathcad

Действия с матрицами.

Построение графика функции.

16. Решение уравнения с одним неизвестным: root(f(х),х); root(f(х),х,а,b).

Для решения уравнения с одним неизвестным в Mathcad, помимо вычислительного блока Given/Find, предусмотрена встроенная функция root, которая, в зависимости от типа задачи, может включать либо два, либо четыре аргумента и, соответственно, использует разные алгоритмы поиска корней.

· f(x) — скалярная функция, определяющая уравнение f(x)=0;

· х — имя скалярной переменной, относительно которой решается уравнение;

· а, b — границы интервала, внутри которого происходит поиск корня.

Первый тип функции root, аналогично встроенной функции Find, требует дополнительного задания начального значения переменной х, для чего нужно просто перед применением функции root присвоить х некоторое число. Таким образом, присвоение начального значения требует априорной информации о примерной локализации корня, т. к. поиск корня будет производиться вблизи этого числа. Пример работы функции root объясняется листингом 5.13.

Листинг 5.13. Два варианта уравнения методом секущих

В чем же отличие встроенной функции Find от функции root? Оно состоит в том, что для решения одних и тех же задач используются различные численные алгоритмы (градиентные и метод секущих соответственно). В примерах уравнений с одним неизвестным, которые мы рассматривали до сего момента, выбор метода не влиял на окончательный результат, поскольку фигурировавшие в них функции были «хорошими», т. е. достаточно гладкими для поиска корня одним из градиентных методов, требующих, как известно, вычисления производных. Между тем бывают ситуации, когда применение того или иного метода имеет решающее значение.

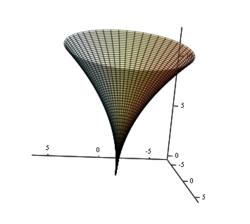
Приведем пример простой функции f(x), корни которой удается отыскать только при помощи функции root (листинг 5.14). Она определена в первой строке этого листинга, а ее корень вычислен во второй строке. Из графика, представленного на рис. 5.5, видно, что f (х) имеет особенность в окрестности своего корня, являясь в ней разрывной. В завершающей части листинга 5.14 предпринимается попытка отыскать нулевое значение f (х) посредством вычислительного блока Given/Find, которая оказывается неудачной.

Листинг 5.14. Пример уравнения, которое удается решить только методом секущих

Рис. 5.5. Модельная функция f (х) (продолжение листинга 5.14)

Таким образом, в обоих случаях один из аргументов функции f (х) воспринимается как неизвестное, а другой — как параметр. Не забывайте при численном решении уравнений относительно одной из переменных предварительно определить значения остальных переменных. Иначе попытка вычислить уравнения приведет к появлению ошибки «This variable or function is not defined above», в данном случае говорящей о том, что другая переменная ранее не определена.

ПРИМЕЧАНИЕ
Для того чтобы отыскать зависимость корней уравнения, вычисленных по одной переменной, от других переменных, разработаны специальные эффективные алгоритмы. Об одной из возможностей читайте в разд. 5.3.3.

Листинг 5.15. Поиск корней уравнения, зависящего от двух переменных

Наложение связей.

Наложение связей в опорных узлах

Для выполнения этой операции во вкладке Назначение инструментальной панели с помощью кнопки Установка связей в узлах вызываем диалоговое окно Связи. В режиме Полная замена активизируем кнопки X, Z, UY(рис. 3.21) и нажимаем кнопку OK. Выделяем курсором на схеме узлы: 1, 2 и нажимаем кнопку Подтверждение инструментальной панели, которая обеспечивает жесткое защемление опорных узлов 1 и 2 рамы в плоскости XоZ. Подобную операцию повторяем для шарнирно-неподвижного узла 3 (активизацией кнопок X, Z). Визуальный контроль правильности постановки опорных связей выполняем нажатием кнопки Связи на панели Фильтры отображения.

Задание нагрузок.

Функции задания нагрузок содержатся в разделе Загружения инструментальной панели.

Режим задания нагрузок включает функции, обеспечивающие автоматическое формирование собственного веса конструкции, задание динамических и статических нагрузок различного вида на узлы и элементы схемы, сохранение назначенных нагрузок в виде схем загружений или групп нагрузок. Зададим нагрузки на учебную расчетную схему в виде двух загружений:

Загружение 1 – описывает постоянную нагрузку на перекрытиях и покрытиях и собственный вес колонн, которые задаются как равномерно распределенная нагрузка на ригели – 4.36 т/м, и равномерно распределенная нагрузка на колонны – 0.66 т/м. Нагрузки задаются по направлению оси Z общей системы координат;

Для задания этих нагрузок воспользуемся следующими кнопками инструментальной панели:

Для ввода нагрузок необходимо выполнить следующие операции:

Для записи загружения надо нажать кнопку в инструментальной панели. В диалоговом окне Сохранить загружение ввести имя загружения и нажать кнопку ОК. Ввод имени не является обязательным, но эта информация позволяет лучше ориентироваться при анализе исходных данных и результатов расчета. Номер загружению будет присваивается автоматически (с согласия пользователя), о чем сообщается в специальном окне.

Перед тем, как ввести следующее загружение, воспользуйтесь операцией – очистка текущего загружения. При ее выполнении происходит очистка схемы от нагрузок текущего загружения. После этого можно готовить новое загружение. Если при записи загружения ему присвоить номер ранее созданного, то оно будет записано вместо него.

Раздел Деформации.

В этом режиме предусмотрено выполнение следующих функций отображения результатов:

– вывод деформированной схемы на фоне исходной;

– вывод деформированной схемы;

– вывод значений перемещений по заданному направлению в узлах расчетной схемы;

– цветовое отображение значений перемещений по заданному направлению в узлах расчетной схемы;

– отображение исходного состояния схемы;

– отображение на проекциях деформированной схемы на фоне исходной;

– вывод изополей перемещений для пластинчатых элементов;

– вывод изополей и изолиний перемещений для пластинчатых элементов;

– вывод изолиний перемещений для пластинчатых элементов;

– установка параметров цветовой шкалы;

– отображение приведенных узловых масс;

– формирование видеоклипов перемещений для статических и динамических загружений;

– анимация перемещений для статических и

После линейного расчета открываем в дереве проекта раздел Результаты, а в нем подраздел «Графический анализ». В открывшемся окне открываем инструментальную панель Деформации и нажимаем кнопку «Совместное отображение исходной и деформированной схемы». Рядом с исходной схемой появится картина деформированной схемы (без указания численных значений перемещений узлов).

Кнопки Параметры вывода.

Для назначения правил формирования и оформления результатов используется кнопка Параметры вывода, после нажатия которой появляется диалоговое окно Состав выходных таблиц.

Из этого окна осуществляется доступ к следующим функциям назначения параметров:

• список узлов или элементов, для которых выводятся результаты;

• параметры настройки генератора таблиц;

• выходные единицы измерения. Параметры настройки задаются в диалоговых окнах, вызов которых выполняется нажатием соответствующих кнопок.

В окне Параметры вывода, которое вызывается после нажатия одноименной кнопки, можно назначить количество строк на странице и ширину таблиц, точность вывода перемещений и усилий, выбрать тип таблицы, определить формат выходного файла, ориентацию страниц, размер шрифта и др.

Используя соответствующую маску вывода, можно настроить программу на печать только определенных видов силовых факторов или перемещений.

Назначение и основные возможности программного пакета MathCAD.

Основные возможности

Mathcad содержит сотни операторов и встроенных функций операторов для решения различных технических задач. Программа позволяет выполнять численные и символьные вычисления, производить операции с скалярными величинами, векторами и матрицами, автоматически переводить одни единицы измерения в другие.

Среди возможностей Mathcad можно выделить:

— Решение дифференциальных уравнений, в том числе и численными методами

— Построение двумерных и трёхмерных графиков функций (в разных системах координат, контурные, векторные и т. д.)

— Использование греческого алфавита как в уравнениях, так и в тексте

— Выполнение вычислений в символьном режиме

— Выполнение операций с векторами и матрицами

— Символьное решение систем уравнений

— Поиск корней многочленов и функций

— Проведение статистических расчётов и работа с распределением вероятностей

— Поиск собственных чисел и векторов

— Вычисления с единицами измерения

— Интеграция с САПР системами, использование результатов вычислений в качестве управляющих параметров

— С помощью Mathcad инженеры могут документировать все вычисления в процессе их проведения.

Источник

Mathcad

Mathcad — система компьютерной алгебры из класса систем автоматизированного проектирования, ориентированная на подготовку интерактивных документов с вычислениями и визуальным сопровождением, отличается легкостью использования и применения для коллективной работы.

Mathcad был задуман и первоначально написан Алленом Раздовом [3] из Массачусетского технологического института (MIT), соучредителем компании Mathsoft, которая с 2006 года является частью корпорации PTC (Parametric Technology Corporation).

Mathcad имеет интуитивный и простой для использования интерфейс пользователя. Для ввода формул и данных можно использовать как клавиатуру, так и специальные панели инструментов.

Некоторые из математических возможностей Mathcad (версии до 13.1 включительно) основаны на подмножестве системы компьютерной алгебры Maple (MKM, Maple Kernel Mathsoft). Начиная с 14 версии — использует символьное ядро MuPAD.

Работа осуществляется в пределах рабочего листа, на котором уравнения и выражения отображаются графически, в противовес текстовой записи в языках программирования. При создании документов-приложений используется принцип WYSIWYG (What You See Is What You Get — «что видишь, то и получаешь»).

Несмотря на то, что эта программа в основном ориентирована на пользователей-непрограммистов, Mathcad также используется в сложных проектах, чтобы визуализировать результаты математического моделирования, путем использования распределённых вычислений и традиционных языков программирования. Также Mathcad часто используется в крупных инженерных проектах, где большое значение имеет трассируемость и соответствие стандартам.

Количество пользователей в мире — около 1.8 млн.

Содержание

Основные возможности

Mathcad содержит сотни операторов и встроенных функций для решения различных технических задач. Программа позволяет выполнять численные и символьные вычисления, производить операции с скалярными величинами, векторами и матрицами, автоматически переводить одни единицы измерения в другие.

Среди возможностей Mathcad можно выделить:

С помощью Mathcad инженеры могут документировать все вычисления в процессе их проведения.

Сравнительная характеристика

Назначение

Mathcad относится к системам компьютерной алгебры, то есть средств автоматизации математических расчетов. В этом классе программного обеспечения существует много аналогов различной направленности и принципа построения. Наиболее часто Mathcad сравнивают с такими программными комплексами, как Maple, Mathematica, MATLAB, а также с их аналогами MuPAD, Scilab, Maxima и др. Впрочем, объективное сравнение осложняется в связи с разным назначением программ и идеологией их использования.

Система Maple, например, предназначена главным образом для выполнения аналитических (символьных) вычислений и имеет для этого один из самых мощных в своем классе арсенал специализированных процедур и функций (более 3000). Такая комплектация для большинства пользователей, которые сталкиваются с необходимостью выполнения математических расчетов среднего уровня сложности, является избыточным. Возможности Maple ориентированы на пользователей — профессиональных математиков; решения задач в среде Maple требует не только умения оперировать какой-либо функции, но и знания методов решения, в неё заложенных: во многих встроенных функциях Maple фигурирует аргумент, задающий метод решения.

Тоже самое можно сказать и о Mathematica. Это одна из самых мощных систем, имеет чрезвычайно большую функциональную наполненность (есть даже синтезирование звука). Mathematica обладает высокой скоростью вычислений, но требует изучения довольно необычного языка программирования.

Разработчики Mathcad сделали ставку на расширение системы в соответствии с потребностями пользователя. Для этого назначены дополнительные библиотеки и пакеты расширения, которые можно приобрести отдельно и которые имеют дополнительные функции, встраиваемые в систему при установке, а также электронные книги с описанием методов решения специфических задач, с примерами действующих алгоритмов и документов, которые можно использовать непосредственно в собственных расчетах. Кроме того, в случае необходимости и при условии наличия навыков программирования в C, есть возможность создания собственных функций и их прикрепления к ядру системы через механизм DLL.

Mathcad, в отличие от Maple, изначально создавался для численного решения математических задач, он ориентирован на решение задач именно прикладной, а не теоретической математики, когда нужно получить результат без углубления в математическую суть задачи. Впрочем, для тех, кому нужны символьные вычисления и предназначено интегрированное ядро Maple (с версии 14 — MuPAD). Особенно это полезно, когда речь идет о создании документов образовательного назначения, когда необходимо продемонстрировать построение математической модели, исходя из физической картины процесса или явления. Символьное ядро Mathcad, в отличие от оригинального Maple (MuPAD), искусственно ограничено (доступно около 300 функций), но этого в большинстве случаев вполне достаточно для решения задач инженерного характера.

Интерфейс

Основное отличие Mathcad от аналогичных программ — это графический, а не текстовый режим ввода выражений. Для набора команд, функций, формул можно использовать как клавиатуру, так и кнопки на многочисленных специальных панелях инструментов. В любом случае — формулы будут иметь привычный, аналогичный книжному, вид. То есть особой подготовки для набора формул не нужно. Вычисления с введенными формулами осуществляются по желанию пользователя или мгновенно, одновременно с набором, либо по команде. Обычные формулы вычисляются слева направо и сверху вниз (подобно чтению текста). Любые переменные, формулы, параметры можно изменять, наблюдая воочию соответствующие изменения результата. Это дает возможность организации действительности интерактивных вычислительных документов.

В других программах (Maple, MuPAD, Mathematica) вычисления осуществляются в режиме программного интерпретатора, который трансформирует в формулы введенные в виде текста команды. Maple своим интерфейсом ориентирован на тех пользователей, кто уже имеет навыки программирования в среде традиционных языков с введением сложных формул в текстовом режиме. Для пользования Mathcad можно вообще не быть знакомым с программированием в том или ином виде.

Mathcad задумывался как средство программирования без программирования, но, если возникает такая потребность — Mathcad имеет довольно простые для усвоения инструменты программирования, позволяющие, впрочем, строить весьма сложные алгоритмы, к чему прибегают, когда встроенных средств решения задачи не хватает, а также когда необходимо выполнять серийные расчеты. [6]

Отдельно следует отметить возможность использования в расчетах Mathcad величин с размерностями, причем можно выбрать систему единиц: СИ, СГС, МКС, английскую, или построить собственную. Результаты вычислений, разумеется, также получают соответствующую размерность. Пользу от такой возможности трудно переоценить, поскольку значительно упрощается отслеживание ошибок в расчетах, особенно в физических и инженерных.

Графика

В среде Mathcad фактически нет графиков функций в математическом понимании термина, а есть визуализация данных, находящихся в векторах и матрицах (то есть осуществляется построение как линий так и поверхностей по точкам с интерполяцией), хотя пользователь может об этом и не знать, поскольку у него есть возможность использования непосредственно функций одной или двух переменных для построения графиков или поверхностей соответственно. Так или иначе, механизм визуализации Mathcad значительно уступает таковому у Maple, где достаточно иметь только вид функции, чтобы построить график или поверхность любого уровня сложности. По сравнению с Maple, графика Mathcad имеет ещё такие недостатки, как: невозможность построения поверхностей, заданных параметрически, с непрямоугольной областью определения двух параметров; создание и форматирование графиков только через меню, что ограничивает возможности программного управления параметрами графики. [6]

Однако следует помнить об основной области применения Mathcad — для задач инженерного характера и создание учебных интерактивных документов, возможностей визуализации вполне достаточно. Опытные пользователи Mathcad демонстрируют возможность визуализации сложнейших математических конструкций, но объективно это уже выходит за рамки назначения пакета.

Расширение функциональности

Возможно дополнение Mathcad новыми возможностями с помощью специализированных пакетов расширений и библиотек, которые пополняют систему дополнительными функциями и константами для решения специализированных задач:

Взаимодействие с другими программами

Mathcad интегрируется с программами SmartSketch, VisSim/ Comm PE, Pro/ENGINEER.

Приложение SmartSketch позволяет инженерам, дизайнерам, архитекторам, чертежникам, системным и сетевым администраторам работать с точными чертежами и графиками.

VisSim/Comm PE — это Windows-приложение для моделирования аналоговых, цифровых или смешанных систем сообщения на сигнальном или физическом уровне.

Использование компонентов

В документах-программах Mathcad есть возможность вставки модулей (component) других приложений для расширения возможностей визуализации, анализа данных, выполнение специфических вычислений.

Для расширенной визуализации данных предназначен компонент Axum Graph. Для работы с табличными данными — Microsoft Excel.

Компоненты Data Acquisition, ODBC Input позволяют пользоваться внешними базами данных.

Предлагаются также бесплатные модули (add-in) для интеграции Mathcad с программами Excel, AutoCAD.

Для статистического анализа предназначен компонент Axum S-PLUS Script.

Значительное расширение возможностей пакета достигается при интеграции со сверхмощным приложением MATLAB.

История версий

Mathcad 1.0-5.xx

3D-графика появилась в версиях 2.5х и выше, возможности которой, впрочем, существенно сдерживались незначительными вычислительными возможностями ЭВМ того времени.

Объединив усилия с фирмой Waterloo Maple Software и введя в свои системы ядро мощной системы символьной математики Maple V, MathSoft Inc. научила свою систему (начиная уже с версии 3.0) основам компьютерной алгебры (символьной математики). Однако, из многочисленных функций ядра Maple V и его расширений (их было около 2500 в Maple V R3 для Windows) привлечено лишь мизерную часть распространенных функций символьной математики. Между тем, появилась возможность использовать функции ядра Maple V с вызовом их из системы Mathcad.

Возможности программирования ограничивались функциями if и until, позволявшие реализовывать лишь две основные алгоритмические конструкции — выбор и повторение. Но эти функции не могут иметь в качестве аргументов блоки составных операторов. Поэтому для реализации даже несложного алгоритма нужно было подключать механизм вложенных функций, существенно осложняющего программирование.

Версии с 5-й и выше уже работали на платформе Windows. Начиная с пятой версии Mathcad пользователям была представлена возможность объявления в среде Mathcad новых встроенных функций. Их нужно было написать на языке С, откомпилировать 32-разрядным транслятором и прикрепить к Mathcad через механизм DLL.

В пятой версии также появились инструменты решения обыкновенных дифференциальных уравнений (ОДУ) и их систем.

Mathcad 6

Версии Mathcad 6.0 и PLUS 6.0 были рассчитаны на работу с ОС Windows 95 и были полноценными 32-разрядными приложениями, которые могли полностью использовать новые возможности микропроцессоров серий 486/Pentium. Интерфейс системы был улучшен, повышена скорость выполнения операций, введены многочисленные новые графические возможности, новые функции и новые возможности программирования.

Вариант системы 6.0 Standard Edition рассчитана на обычных пользователей, к которым относятся ученые, инженеры, преподаватели и студенты вузов, уважающие математику, но не считающие всё же её главным своим занятием. Система ориентирована на ПК класса 386DX и выше с емкостью RAM не менее 4 Мб и свободным пространством на диске не менее 12 Мб для файла подкачки и ещё 20 Мб для установки самой системы.

Второй вариант системы — PLUS 6.0 — ориентирован на пользователей-профессионалов, которым требуется более мощный математический помощник. Для реализации расширенных возможностей становится необходимым RAM с емкостью не менее 8 Мб. Mathcad PLUS 6.0 имеет заметно расширенный набор функций (20 новых матричных функций, 13 функций для решения дифференциальных уравнений различного типа, ряд новых статистических функций и т. д.), расширенные возможности символьных вычислений и мощную графику. Стоимость Mathcad 6.0 составляла 129$, а Mathcad PLUS 6.0 — 495$. Были также версии для студентов и школьников (Mathcad 6.0 BASIC, 90$), Mathcad 6.0 Standart (240$). Для версий Standart и PLUS дополнительно включалось средство рисования технических и бизнес-диаграмм Visio Express корпорации Visio.

Mathcad 7

В версии Mathcad 7.0 PRO были следующие доработки и нововведения: отсутствие проблемы 2000 года; интерфейс, существенно переработанный и приближенный к интерфейсу текстового процессора Word 95/97; выделения частей выражений мышью; задание впервые для данной переменной её значения или значений нажатием клавиши = (при этом на экране выводится знак присваивания :=), при повторном использовании клавиши = для этой же переменной выводится её текущее значение; быстрое построение (QuickPlot) графиков в декартовых и полярных координатах с автоматической установкой пределов изменения независимых переменных; новая палитра символьной математики с расширенными операторами; удобным и наглядным синтаксисом символьных операций; возможность обработки ошибок в ходе вычислений; новые инструкции on error, continue, return; применение в программах операторов символьных операций; новый тип строковых данных, констант и переменных; восемь новых функций для работы со строковыми данными; задачи размерных величин в системе СИ; возможность подготовки сложных документов различными пользователями, работающими в разных местах, с помощью Collaboratory; возможность обмена документами через Интернет; появление более оперативного центра ресурсов (Resource Center) вместо «быстрых шпаргалок» QuickSheet, электронных книг, самоучителя и др.; моделирование (симуляция) работы сложных систем, построенных из функциональных блоков, с помощью системы MathConnex, имеющая 16 компонентов; возможность использования функций других систем (Excel, Axum, MATLAB и др.) и фактическая интеграция с ними.

Некоторые из указанных изменений были скорее из разряда приятных мелочей, например расширено действие знака = (ранее для присвоения переменным значений нужно было вводить только комбинированный знак :=). Другие изменения, такие как интеграция с другими системами и применение системного интегратора MathConnex, были серьёзными дополнением системы, открыли множество новых возможностей.

Mathcad 8

Версия Mathcad 8.0 PRO предоставила ещё целый ряд полезных возможностей: около 50 новых математических функций (элементарных, специальных статистических и др.); новые функции оптимизации maximize и minimize; решения задач линейного программирования, новые функции контроля типа данных; улучшенный блок решения систем нелинейных уравнений — снято ограничение на полное число уравнений (ранее было не более 50), теперь их число достигло 200; введение набора методов численного интегрирования с возможностью выбора конкретного метода через контекстное меню; возможность проведения бинарных вычислений; эффективные средства сглаживания данных; улучшенные средства ввода и форматирования текста; команды редактирования Find (найти) и Replace (найти и заменить); новая возможность блокировки и сокрытия областей; улучшенное вывода таблиц; возможность записи документов в формате HTML, возможность записи документов в формате предыдущих версий; поддержка новой графики OpenGL и ActiveX, применение мастеров для создания сложных трехмерных графиков; существенно улучшены средства форматирования графиков; просмотр графиков в увеличенном масштабе; применения функциональной окраски поверхностей; возможность изображения на одном трехмерном графике поверхностей и фигур разного типа; возможность изображения на одном трехмерном графике разных объектов, с пересечением в пространстве; возможность вращения трехмерных графиков в пространстве мышью; анимация трехмерных графиков.

Mathcad 2000 (версия 9)

Версия Mathcad 2000 добавила к существующим возможностям ещё ряд новых и существенных отличий: улучшенный интерфейс системы, в частности интеграция с Интернетом перенесена в центр ресурсов; введен ряд новых функций для финансово-экономических расчетов, создания матриц трехмерных поверхностей, численного решения дифференциальных уравнений в составе блока Given, контроля типа размерных переменных и др.; введен набор функций для выполнения регрессии — экспоненциальной, логарифмической, синусоидальной и др.; введен набор логических операторов; расширенные возможности функции root — теперь она может искать корень не только по заданному приближению (функция с двумя параметрами), но и в заданном интервале (функция с четырьмя параметрами); введено ускоренное и упрощенное построение трехмерных графиков; предусмотрено наложение надписей на блоки документов, в частности графические; введена трассировка ошибок; существенно обновлен набор примеров в центре ресурсов; обеспечен контроль орфографии англоязычных текстов на трех диалектах английского языка.

Mathcad 2001 (версия 10)

В версии Mathcad 2001 ещё более возросла производительность вычислений и расширились возможности. Внедрена поддержка Windows 2000. Созданы четыре модификации с учетом специфики использования.

Основные нововведения: расширение совместимости с другими популярными приложениями; обработка единиц измерения в реальном времени; ограничения рекурсивного спуска в процессе вычислений (выигрыш в скорости до 5-20 раз по сравнению с предыдущими версиями); оптимизированы вычисления, особенно для итераций, суммирования, интегрирования и дифференцирования; новые логические алгоритмы, основанные на зависимостях от областей изменения переменных и большая согласованность между аналитическими и численными расчетами; улучшенное управление памятью и обработка объектов рабочего документа, которые удаляются; новый режим публикации в сочетании с основанными на MathML возможностями электронных публикаций; включение последней версии IBM Techexplorer Professional Edition для чтения и редактирования MathML, TeX и LaTeX.

Существенно усовершенствованы инструменты для создания приложений с использованием Mathcad: улучшенные объекты программирования сценария для создания новых модулей из программируемых OLE и COM объектов, а также хранение их для повторного использования и распространения. Поддерживаются стандартные языки программирования сценариев, такие как VBScript и JScript.

Mathcad 2001i («интерактивный»)

Mathcad 2001i получил полную поддержку Windows XP, расширены возможности сбора данных от внешних устройств, повышенную защищенность Mathcad-документов введением современной криптографии, упрощенную публикацию в Интернет, расширенное число алгоритмов решения задач и набор опций пользовательских настроек.

Mathcad 11-11.2a

При создании Mathcad 11 основное внимание было обращено на увеличение скорости и мощности работы системы. Цель состояла в том, чтобы улучшить ядро Mathcad, расширить и улучшить удобства работы с Mathcad.

Mathcad 12

Новая версия пакета получила более совершенное математическое ядро, а также дополнительные опции, позволяющие сохранять и публиковать документы Mathcad в различных форматах.

Mathcad 13-13.1

Mathcad 14

Mathcad 14 — первая с момента приобретения Mathsoft Inc. компанией PTC версия Mathcad (релиз состоялся 12 февраля 2007). Реализована возможность двусторонней интеграции с основным продуктом PTC — пакетом Pro/ENGINEER. Базовые величины, рассчитанные в системе Mathcad, могут быть переведены в параметры и размеры CAD-модели для управления геометрическим объектом. Параметры из модели Pro/ENGINEER также можно ввести в Mathcad для последующих инженерно-конструкторских расчетов.

Существенные изменения коснулись также математического ядра системы, которое теперь использует символьную систему MuPAD. Это позволило во многих случаях повысить точность символьных вычислений и их детализацию, но есть и негативные последствия, связанные, в первую очередь, с совместимостью символьных алгоритмов с предыдущими версиями (вычисления, которые работают в предыдущих версиях, могут не выполняться в новой и наоборот).

Версии Mathcad с 12-й включительно, в связи с использованием формата данных XML, а также с постепенным ростом функционального инструментария, имеют ограниченную обратную совместимость документов с предыдущими версиями, но могут почти без ограничений открывать документы, созданные в старых версиях. Как следствие, импорт также имеет ограничения: документ, созданный в Mathcad 14 можно сохранить в формате версии не ниже 11-й.

Mathcad 15

Основные новые возможности:

Mathcad Prime 1.0

Mathcad Prime 1.0 является последним релизом компании PTC в программном обеспечении для инженерных расчетов. Основные отличия нового Mathcad Prime 1.0 [9] :

Комплектации

Версии Mathcad могут отличатся комплектацией и лицензией пользователя. В разное время поставлялись версии Mathcad Professional, Mathcad Premium, Mathcad Enterprise Edition (отличаются комплектацией). Для академических пользователей предназначена версия Mathcad Academic Professor (обладает полной функциональностью, но отличается лицензией пользователя и имеет в несколько раз меньшую стоимость).

Некоторое время выпускались также упрощенные и заметно «урезанные» студенческие версии программы.

Развитие

Дальнейшее развитие технология Mathcad получила при создании Mathcad Application Server (MAS). Суть технологии MAS — в реализации удаленного доступа к программному обеспечению Mathcad или уже готовым Mathcad-документам через веб-интерфейс (технология Web Calc). Пользователь MAS не нуждается в покупке Mathcad, не требуется скачивать и запускать exe-файлы (но это не исключается и определяется уровнем доступа).

Источник