Что такое магнитные силы

Магнитное поле

Магнитное поле играет очень большую роль в электротехнике и электронике. Без магнитного поля не функционировали бы герконы, электромагнитные реле, соленоиды, катушки индуктивности, дроссели, трансформаторы, двигатели, динамики, генераторы электрической энергии да и вообще много чего.

Природа магнетизма

Согласно одной из легенд, когда-то давным-давно жил в Греции пастух по имени Магнес. И вот шел он как-то со своим стадом овец, присел на камень и обнаружил, что конец его посоха, сделанный из железа, стал притягиваться к этому камню. С тех пор стали называть этот камень магнетит в честь Магнеса. Этот камень представляет из себя оксид железа.

Если такой камень положить на деревянную доску на воду или подвесить на нитке, то он всегда выстраивался в определенном положении. Один его конец всегда показывал на СЕВЕР, а другой — на ЮГ.

Этим свойством камня пользовались древние цивилизации. Поэтому, это был своего рода первый компас. Потом уже стали обтачивать такой камень и делать из разные фигурки. Например, так выглядел китайский древний компас, ложка которого была сделана из того самого магнетита. Ручка у этой ложки всегда показывала на ЮГ.

Ну а далее дело шло за практичностью и маленькими габаритами. Из магнетита вытачивали маленькие стрелки, которые подвешивали на тонкую иглу посередине. Так стали появляться первые малогабаритные компасы.

Древние цивилизации, конечно, не знали еще что такое север и юг. Поэтому, одну сторону магнетита они назвали северным полюсом (North), а противоположный конец — южным (South). Названия на английском очень легко запомнить, если кто смотрел американский мультфильм «Южный парк», он же Сауз (South) парк).

Магнитные линии и магнитный поток

Вокруг магнита экспериментальным путем были обнаружены магнитные силовые линии. Эти магнитные линии создают так называемое магнитное поле.

Как вы могли заметить на рисунке, концентрация магнитных силовых линий на самых краях магнита намного больше, чем в его середине. Это говорит о том, что магнитное поле является более сильным именно на краях магнита, а в его середине практически равна нулю. Направлением магнитных силовых линий считается направление от севера к югу.

Ошибочно считать, что магнитные силовые линии начинают свое движение от северного полюса и заканчивают свой век на южном. Это не так. Магнитные линии — они замкнуты и непрерывны. В магните это будет выглядеть примерно так.

Если приблизить два разноименных полюса, то произойдет притягивание магнитов

Если же приблизить одноименными полюсами, то произойдет их отталкивание

Итак, ниже важные свойства магнитных силовых линий.

Магнитные силовые линии, которые образуют магнитное поле, называют также магнитным потоком.

Итак, давайте рассмотрим два рисунка и ответим себе на вопрос, где плотность магнитного потока будет больше? На рисунке «а» или на рисунке «б»?

Видим, что на рисунке «а» мало силовых магнитных линий, а на рисунке «б» их концентрация намного больше. Отсюда можно сделать вывод, что плотность магнитного потока на рисунке «б» больше, чем на рисунке «а».

В физике формула магнитного потока записывается как

Ф — магнитный поток, Вебер

В — плотность магнитного потока, Тесла

а — угол между перпендикуляром n (чаще его зовут нормалью) и плоскостью S, в градусах

S — площадь, через которую проходит магнитный поток, м 2

Что же такое 1 Вебер? Один вебер — это магнитный поток, который создается полем индукцией 1 Тесла через площадку 1м 2 расположенной перпендикулярно направлению магнитного поля.

Напряженность магнитного поля

Формула напряженности

Слышали ли вы когда-нибудь такое выражение: «напряженность между ними все росла и росла». То есть по сути напряженность — это что-то невидимое, какая-то сдерживающая сила, энергия. Здесь почти все то же самое. Напряженностью магнитного поля также часто называют силой магнитного поля. Напряженность магнитного поля напрямую зависит от плотности магнитного потока и выражается формулой

H — напряженность магнитного поля, Ампер/метр

B — плотность магнитного потока, Тесла

Эта формула работает только тогда, когда между витками катушки находится воздух, либо вакуум. Более крутая формула выглядит вот так.

μ — это относительная магнитная проницаемость.

У разных веществ она разная

Напряженность магнитного поля проводника с током

Итак, имеем какой-либо проводник, по которому течет электрический ток.

Для того, чтобы вычислить напряженность магнитного поля на каком-то расстоянии от проводника при условии, что проводник находится в воздушном пространстве либо в вакууме, достаточно воспользоваться формулой

H — напряженность магнитного поля, Ампер/метр

I — сила тока, текущая через проводник, Ампер

r — расстояние до точки, в которой измеряется напряженность, метр

Магнитное поле проводника с током

Оказывается, если через какой-либо проводник пропустить электрический ток, то вокруг проводника образуется магнитное поле.

Здесь можно вспомнить знаменитое правило буравчика, но для наглядности я лучше буду использовать правило самореза, так как почти все хоть раз в жизни ввинчивали либо болт, либо саморез.

Ввинчиваем по часовой стрелке — саморез идет вниз. В нашем случае он показывает направление электрического тока. Движение наших рук показывает направление линий магнитного поля. Все то же самое, когда мы начинаем откручивать саморез. Он начинает вылазить вверх, то есть в нашем случае показывает направление электрического тока, а наша рука в этом время рисует в воздухе направление линий магнитного поля.

Также часто в учебниках физики можно увидеть, что направление электрического тока от нас рисуют кружочком с крестиком, а к нам — кружочком с точкой. В этом случае опять представляем себе саморез и уже в голове увидим направление магнитного поля.

Как думаете, что будет если мы сделаем вот такую петельку из провода? Что изменится в этом случае?

Давайте же рассмотрим этот случай более подробно. Так в этой плоскости оба проводника создают магнитное поле, то по идее они должны отталкиваться друг от друга. Но если они хорошо закреплены, то начинается самое интересное. Давайте рассмотрим вид сверху, как это выглядит.

Как вы можете заметить, в области, где суммируются магнитные силовые линии плотность магнитного потока прям зашкаливает.

Соленоид

А что если сделать много-много таких петелек? Взять какую-нибудь круглую бобину, намотать на нее провод и потом убрать бобину. У нас должно получится что-то типа этого.

Если подать постоянное напряжение на такую катушку, магнитные силовые линии будут выглядеть вот так.

Вы только посмотрите, какая бешеная плотность магнитного потока внутри такой катушки! Получается, что от каждой петельки магнитное поле суммируется, что в итоге дает такую плотность магнитного потока. Такую катушку также называют катушкой индуктивности или соленоидом.

Вот также схема, показывающая как магнитные силовые линии складываются в соленоиде.

Плотность магнитного потока зависит от того, какая сила тока проходит через соленоид. Чтобы увеличить плотность магнитного потока, достаточно поверх витков намотать еще больше витков и вставить сердечник из специального материала — феррита.

Если в электрических цепях есть такое понятие, как ЭДС — электродвижущая сила, то и в магнитных цепях есть свой аналог — МДС — магнитодвижущая сила. Магнитодвижущая сила выражается в виде тока, протекающего через катушку из N витков и выражается в Амперах-витках.

I — это сила тока в катушке, Амперы

N — количество витков катушки, штуки)

Также советую посмотреть очень простое и интересное видео про магнитное поле.

Похожие статьи по теме «магнитное поле»

Источник

Представление о магнитном поле

Мы все знаем, что такое постоянные магниты. Магниты – это металлические тела, притягивающиеся к другим магнитам и к некоторым металлам. То, что располагается вокруг магнита и взаимодействует с окружающими предметами (притягивает или отталкивает некоторые из них), называется магнитным полем.

Источником любого магнитного поля являются движущиеся заряженные частицы. А направленное движение заряженных частиц называется электрическим током. То есть, любое магнитное поле вызывается исключительно электрическим током.

За направление электрического тока принимают направление движения положительно заряженных частиц. Если же движутся отрицательные заряды, то направление тока считается обратным движению таких зарядов. Представьте себе, что по кольцевой трубе течет вода. Но мы будем считать, что некий «ток» при этом движется в противоположном направлении. Электрический ток обозначается буквой I.

В металлах ток образуется движением электронов – отрицательно заряженных частиц. На рисунке ниже, электроны движутся по проводнику справа налево. Но считается, что электрический ток направлен слева направо.

Это произошло потому, что когда начали изучение электрические явления, не было известно, какими именно носителями чаще всего переносится ток.

Если мы посмотрим на этот проводник с левой стороны, так, чтобы ток шел «от нас», то магнитное поле этого тока будет направлено вокруг него по часовой стрелке.

Если рядом с этим проводником расположить компас, то его стрелка развернется перпендикулярно проводнику, параллельно «силовым линиям магнитного поля» — параллельно черной кольцевой стрелке на рисунке.

Если мы возьмем шарик, имеющий положительный заряд (имеющий дефицит электронов) и бросим его вперед, то вокруг этого шарика появится точно такое же кольцевое магнитное поле, закручивающееся вокруг него по часовой стрелке.

Ведь здесь тоже имеет место направленное движение заряда. А направленное движение зарядов есть электрический ток. Если есть ток, вокруг него должно быть магнитное поле.

Движущийся заряд (или множество зарядов – в случае электрического тока в проводнике) создает вокруг себя «тоннель» из магнитного поля. Стенки этого «тоннеля» «плотнее» вблизи движущего заряда. Чем дальше от движущегося заряда, тем слабее напряженность («сила») создаваемого им магнитного поля. Тем слабее реагирует на это поле стрелка компаса.

Закономерность распределение напряженности магнитного поля вокруг его источника такая же, как закономерность распределения электрического поля вокруг заряженного тела – она обратно пропорциональна квадрату расстояния до источника поля.

Если положительно заряженный шарик перемещается по кругу, то кольца магнитных полей, образующихся вокруг него по мере его движения, суммируются, и мы получим магнитное поле, направленное перпендикулярно плоскости, в которой перемещается заряд:

Магнитный «тоннель» вокруг заряда оказывается свернутым в кольцо и напоминает по форме тор (бублик).

Такой же эффект получается, если свернуть в кольцо проводник с током. Проводник с током, свернутый в многовитковую катушку называется электромагнитом. Вокруг катушки складываются магнитные поля движущихся в ней заряженных частиц — электронов.

А если заряженный шарик вращать вокруг его оси, то у него появится магнитное поле, как у Земли, направленное вдоль оси вращения. В данном случае током, вызывающим появление магнитного поля, является круговое движение заряда вокруг оси шарика – круговой электрический ток.

Здесь, по сути, происходит то же самое, что и при движении шарика по кольцевой орбите. Только радиус этой орбиты уменьшен до радиуса самого шарика.

Все сказанное выше справедливо и для шарика заряженного отрицательно, но его магнитное поле будет направлено в противоположную сторону.

Данный эффект был обнаружен в опытах Роуланда и Эйхенвальда. Эти господа регистрировали магнитные поля вблизи вращающихся заряженных дисков: рядом с этими дисками начинала отклоняться стрелка компаса. Направления магнитных полей в зависимости от знака заряда дисков и направления их вращения, показаны на рисунке:

При вращении незаряженного диска, магнитные поля не обнаруживались. Не было магнитных полей и вблизи неподвижных заряженных дисков.

Модель магнитного поля движущегося заряда

Чтобы запомнить направление магнитного поля движущегося положительного заряда, мы представим себя на его месте. Поднимем правую руку вверх, затем укажем ею направо, затем опустим ее вниз, затем укажем влево и вернем руку в исходное положение – вверх. Затем повторим это движение. Наша рука описывает круги по часовой стрелке. Теперь начнем движение вперед, продолжая вращать рукой. Движение нашего тела – аналог движения положительного заряда, а вращение руки по часовой стрелке – аналог магнитного поля заряда.

Теперь представьте себе, что вокруг нас находится тонкая и прочная эластичная паутина, похожая на струны пространства, которые мы рисовали, создавая модель электрического поля.

Когда мы движемся сквозь эту трехмерную «паутину», из-за вращения руки, она, деформируясь, смещается по часовой стрелке, образуя подобие спирали, словно бы наматываясь в катушку вокруг заряда.

Сзади, за нами, «паутина» восстанавливает свою правильную структуру. Примерно так можно представлять себе магнитное поле положительного заряда, движущегося прямо.

А теперь попробуйте двигаться не прямо вперед, а по кругу, например, поворачивая при ходьбе налево, при этом вращая рукой по часовой стрелке. Представьте себе, что вы движетесь через нечто, напоминающее желе. Из-за вращения вашей руки, внутри круга, по которому вы движетесь, «желе» будет смещаться вверх, образуя горб над центром круга. А под центром круга, образуется впадина из-за того, что часть желе сместилось вверх. Так можно представлять себе формирование северного (горб сверху) и южного (впадина снизу) полюсов при движении заряда по кольцу или его вращения.

Если при ходьбе вы будете поворачивать направо, то «горб» (северный полюс) сформируется снизу.

Аналогично можно сформировать представление о магнитном поле движущегося отрицательного заряда. Только вращать рукой нужно в противоположную сторону – против часовой стрелки. Соответственно, магнитное поле будет направлено в противоположную сторону. Просто каждый раз следите за тем, в какой сторону ваша рука выталкивает «желе».

Такая модель наглядно демонстрирует то, почему северный полюс одного магнита притягивается к южному полюсу другого магнита: «горб» одного из магнитов втягивается во «впадину» второго магнита.

И еще эта модель показывает, почему не существуют отдельных северных и южных полюсов магнитов, как бы мы их не разрезали – магнитное поле представляет собой вихревую (замкнутую) «деформацию пространства» вокруг траектории движущегося заряда.

У электрона было обнаружено магнитное поле, такое, какое у него должно быть в том случае, если бы он был шариком, вращающимся вокруг своей оси. Это магнитное поле назвали спином (от английского to spin — вращаться).

Кроме того, у электрона существует еще и орбитальный магнитный момент. Ведь электрон не только «вращается», но движется по орбите вокруг ядра атома. А движение заряженного тела порождает магнитное поле. Так как электрон заряжен отрицательно, магнитное поле, вызванное его движением по орбите, будет выглядеть так:

Если направление магнитного поля, вызванного движением электрона по орбите, совпадает с направлением магнитного поля самого электрона (его спином), эти поля складываются и усиливаются. Если же эти магнитные поля направлены в разные стороны, они вычитаются и ослабляют друг друга.

Кроме того, могут суммироваться или вычитаться друг из друга магнитные поля других электронов атома. Этим объясняется наличие или отсутствие магнетизма (реакции на внешнее магнитное поле или наличие собственного магнитного поля) некоторых веществ.

Эта статья — отрывок из книги об азах химии. Сама книга здесь:
sites.google.com/site/kontrudar13/himia

UPD: Материал предназначен, в первую очередь, для школьников средних классов. Возможно, Хабр не место для подобных вещей, Но где место? Нет его.

Источник

Учебники

Журнал «Квант»

Общие

Ромишевский Е. Эта загадочная магнитная сила //Квант. — 1999. — № 3. — С. 39-40.

По специальной договоренности с редколлегией и редакцией журнала «Квант»

Опытно установлено, что сила, действующая на точечный электрический заряд q, помещенный в электрическое и магнитное поля, зависит в общем случае от положения этого заряда и от его скорости движения. Обычно эту силу разделяют на две составляю- щие — электрическую \(

\vec F_e = q \vec E\), которая не зависит от движения заряда, а определяется его положением в электрическом поле с напряженностью \(

\vec F_m\), зависящую от скорости заряда \(

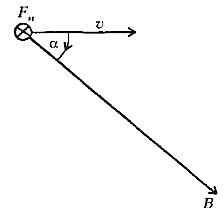
В любой точке пространства магнитная сила перпендикулярна вектору скорости заряда. Перпендикулярна она также и определенному выбранному в пространстве направлению. Величина же магнитной силы (ее модуль) пропорциональна той составляющей скорости заряда, которая перпендикулярна этому выделенному направлению. Эти свойства магнитной силы можно описать, пользуясь понятием магнитного поля. Магнитное поле характеризуется вектором магнитной индукции \(

\vec B\), который и определяет выбранное направление в пространстве.

Для определения магнитной силы можно записать следующее выражение:

\vec B\) и который мы закручиваем, поворачивая его на наименьший угол от вектора \(

\vec \upsilon\) к вектору \(

\vec B\) (рис.1). Магнитная сила \(

\vec F_m\) перпендикулярна и вектору \(

Полную электромагнитную силу \(

\vec F = \vec F_e + \vec F_m\), действующую на электрический заряд q, называют силой Лоренца (заметим, что иногда силой Лоренца называют лишь магнитную силу). По действию силы Лоренца на электрический заряд известного знака можно, в принципе, определить модули и направления векторов \(

Следует особо отметить, что на покоящийся электрический заряд магнитное поле не действует. Важной особенностью магнитной силы является также то, что она всегда перпендикулярна вектору скорости заряда, поэтому работы над зарядом не совершает. Это означает, что в постоянном магнитном поле кинетическая энергия заряженной частицы всегда остается неизменной, как бы частица ни двигалась.

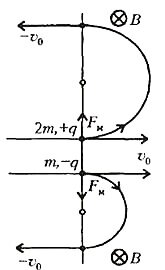
Рассмотрим, например, как будут двигаться две разноименно заряженные частицы с зарядами +q и —q, имеющие разные массы M₁ = 2m и M₂ = m, если в начальный момент скорости этих частиц равны \(

\vec \upsilon_0\) и направлены перпендикулярно границе области существования однородного магнитного поля с индукцией \(

\vec B\)-перпендикулярен плоскости листа и направлен от нас). На оказавшуюся в области однородного магнитного поля положительную частицу действует магнитная сила, равная \(

F_m = q \upsilon_0 B\) и направленная вначале вверх. На отрицательную частицу действует такая же по величине сила, но направленная вначале вниз. Каждая из частиц опишет полуокружность, после чего покинет область магнитного поля. Радиус окружности можно найти из второго закона Ньютона:

Угловая скорость движения частицы по окружности и период ее полного обращения будут равны

Видно, что положительная частица (M₁ = 2m) опишет полуокружность в два раза большего радиуса, чем отрицательная (M₂ = m), которая будет двигаться в противоположную сторону. Возвратится же обратно тяжелая частица (зеркально отразившись) через промежуток времени, в два раза больший, чем отрицательная. Таким образом, однородное магнитное поле как бы разделяет в пространстве и во времени влетевшие вместе, но разные по заряду и по массе частицы.

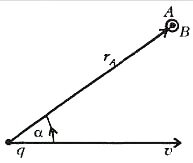
Если магнитное поле воздействует только на движущиеся заряды, то, как показывает опыт, движущиеся заряды (электрические токи), в свою очередь, всегда возбуждают в пространстве магнитное поле. В результате обобщения экспериментальных данных был получен элементарный закон, определяющий индукцию \(

\vec B\) магнитного поля точечного заряда q, движущегося с постоянной скоростью \(

\vec \upsilon\) и радиусом-вектором \(

\vec \upsilon\) к вектору \(

\vec r\) (рис.3) и отвечающий за направление вектора \(

\frac<1><\varepsilon_0 c^2>\) обычно обозначают μ₀ и называют магнитной постоянной.

Заметим, что если умножить обе части приведенной формулы на число электронов \(

\Delta N = n \Delta l S\), находящихся в элементе провода длиной Δl, по которому течет ток \(

\Delta \vec B\) магнитного поля, созданного элементом тока \(

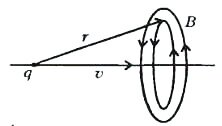
Линии магнитной индукции в данном случае представляют собой концентрические окружности, окружающие линию движения заряда (рис.4), а величина магнитной индукции убывает с расстоянием пропорционально \(

Рассмотрим теперь такой пример.

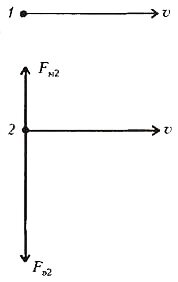
Пусть две достаточно массивные точечные частицы 1 и 2, заряженные одним и тем же зарядом q, движутся параллельно друг другу с одинаковыми нерелятивистскими скоростями \(

\vec \upsilon\) (рис.5). На каждую частицу действуют электрическая сила отталкивания, равкал \(

F_e = qE\), и магнитная сила притяжения, равная \(

F_m = q \upsilon B\) (скорость одной частицы перпендикулярна магнитному полю, создаваемому другой частицей). Сравним количественно эти две составляющие общей электромагнитной силы Лоренца, действующей, к примеру, на частицу 2:

А что если выбрать другую инерциальную систему отсчета, движущуюся равномерно и прямолинейно со скоростью \(

\vec \upsilon\) наших заряженных частиц? В этой системе заряды будут покоиться, пропадут их магнитные поля, пропадет и магнитная сила их взаимодействия. Иными словами, поскольку магнитная составляющая силы Лоренца зависит от скорости частицы, она изменяется при переходе от одной инерциальной системы отсчета к другой. Вместе с тем, сама сила Лоренца в нерелятивистском случае, как любая другая сила, не зависит от выбора инерциальной системы отсчета. Это означает, что в системе отсчета, в которой пропадает магнитная составляющая силы, должна изменяться и электрическая ее составляющая. Получается, что разделение полной силы Лоренца на электрическую и магнитную составляющие без указания конкретной системы отсчета не имеет смысла.

После рассмотренного нами примера движения двух заряженных частиц может возникнуть естественный вопрос — стоит ли вообще изучать и учитывать такие относительно малые магнитные силы? Оказывается, стоит, и вот почему.

Во-первых, полученное соотношение сил справедливо и при релятивистских скоростях υ

с, а тогда магнитные силы оказываются уже сравнимыми с электрическими. Так происходит, например, когда мы имеем дело с пучками быстрых заряженных частиц.

Во-вторых, бывают ситуации, когда ничтожная по величине магнитная сила является единственной действующей силой. Например — при движении электронов вдоль проводов (электрические токи), ибо в этом случае электрические силы отсутствуют в результате почти идеального баланса отрицательных и положительных зарядов в проводниках. Кроме того, участие в создании электрического тока громадного числа носителей зарядов (их примерно 10 23 в одном кубическом сантиметре проводника) делает магнитную силу весьма значительной.

В-третьих, приходится встречаться с движением заряженных частиц в самых разных по величине внешних электрических и магнитных полях, создаваемых различным образом. В этих случаях соотношения между электрическими и магнитными силами могут быть самыми разнообразными.

Источник