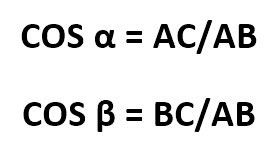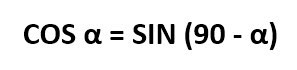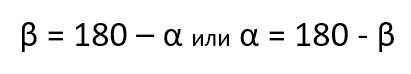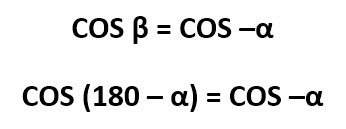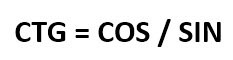Что такое косинус икс

Основное тригонометрическое тождество

9 класс, 10 класс, ЕГЭ/ОГЭ

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Связь между sin и cos одного угла

Вы уже наверняка знаете, что тождественный — это равный.

Основные тригонометрические тождества — это равенства, которые устанавливают связь между синусом, косинусом, тангенсом и котангенсом одного угла. Это значит, что любую из этих функций можно найти, если известна другая функция.

Ключ к сердцу тригонометрии — основное тригонометрическое тождество. Запомните и полюбите его, чтобы отношения с тригонометрией сложились самым наилучшим образом:

sin 2 α + cos 2 α = 1

Из основного тождества вытекают равенства тангенса и котангенса, поэтому оно — ключевое.

Равенство tg 2 α + 1 = 1/cos 2 α и равенство 1 + сtg 2 α + 1 = 1/sin 2 α выводят из основного тождества, разделив обе части на sin 2 α и cos 2 α.

В результате деления получаем:

Поэтому основному тригонометрическому тождеству уделяется максимум внимания. Но какая же «метрия» может обойтись без доказательств. Видите тождество — доказывайте, не раздумывая.

sin 2 α + cos 2 α = 1

Сумма квадратов синуса и косинуса одного угла тождественно равна единице.

Чтобы доказать тождество, обратимся к теме единичной окружности.

Единичная окружность — это окружность с центром в начале прямоугольной декартовой системы координат. Радиус единичной окружности равен единице.

Докажем тождество sin 2 α + cos 2 α = 1

Образовался прямоугольный треугольник OA₁B.

Основное тригонометрическое тождество связывает синус угла и косинус угла. Зная одно, вы легко можете найти другое. Нужно лишь извлечь квадратный корень по формулам:

Как видите, перед корнем может стоять и минус, и плюс. Основное тригонометрическое тождество не дает понять, положительным или отрицательным был исходный синус/косинус угла.

Как правило, в задачках с подобными формулами уже есть условия, которые помогают определиться со знаком. Обычно такое условие — указание на координатную четверть. Таким образом без труда можно определить, какой знак нам требуется.

Тангенс и котангенс через синус и косинус

Из всего этого множества красивых, но не сильно понятных слов, можно сделать вывод о зависимости одного от другого. Такая связь помогает отдельно преобразовывать нужные величины.

Исходя из определений:

Это позволяет сделать вывод, что тригонометрические тождества

задаются sin и cos углов.

Отсюда следует, что тангенс угла — это отношение синуса угла к косинусу. А котангенс угла — это отношение косинуса к синусу.

Отдельно стоит обратить внимание на то, что тригонометрические тождества

верны для всех углов α, значения которых вписываются в диапазон.

применимо для любого угла α, не равного π * z, где z — это любое целое число.

Связь между тангенсом и котангенсом

Уж насколько очевидной кажется связь между ранее рассмотренными тождествами, настолько еще более наглядна связь между тангенсом и котангенсом одного угла.

Такое тождество применимо и справедливо при любых углах α, значение которых не равняются π/2 * z, где z — это любое целое число. В противном случае, функции не будут определены.

Как и любое другое, данное тригонометрическое тождество подлежит доказательству. Доказывать его очень просто.

tg α * ctg α = 1.

Получается, что тангенс и котангенс одного угла, при котором они имеют смысл — это взаимно обратные числа.

Если числа a и b взаимно обратные — это значит, что число a — это число, обратное числу b, а число b — это число, обратное числу a. Кроме того, это значит, что числу a обратно число b, а числу b обратно число a. Короче, и так, и эдак.

Тангенс и косинус, котангенс и синус

Все тождества выше позволяют сделать вывод, что тангенс угла связан с косинусом угла, а котангенс угла — с синусом.

Эта связь становится очевидна, если взглянуть на тождества:

Сумма квадрата тангенса угла и единицы равна числу, обратному квадрату косинуса этого угла.

Сумма единицы и квадрата котангенса угла равна числу, обратному квадрату синуса этого угла.

Вывести оба этих тождества можно из основного тригонометрического тождества:
sin 2 α + cos 2 α = 1.

Хорошо бы выучить все формулы и запомнить формулировки тождеств наизусть. Чтобы это сделать, сохраняйте себе табличку с основными формулами.

Основные тригонометрические тождества

sin 2 α + cos 2 α = 1

tg 2 α + 1 =

1 + ctg 2 α =

Чтобы тратить еще меньше времени на решение задач, сохраняйте таблицу значений тригонометрических функции углов, которые чаще всего встречаются в задачах.

Примеры решения задач

Разберем пару задачек, для решения которых нужно знать основные тождества. Рассмотрите внимательно предложенные решения и потренируйтесь самостоятельно.

Задачка 1. Найдите cos α, tg α, ctg α при условии, что sin α = 12/13.

Задачка 2. Найдите значение cos α,
если:

Подставляем значения sin α:

Как видите, задачи решаются достаточно просто, нужно лишь верно применять формулы основных тождеств.

Источник

Синус, косинус, тангенс и котангенс (ЕГЭ 2022)

Понятия синуса, косинуса, тангенса, котангенса неразрывно связаны с понятием угла.

Не так страшен черт, как его малюют!

Чтобы хорошо разобраться в этих понятиях (нет, не в чёрте! в тригонометрии 🙂 ), начнём с самого начала.

Синус, косинус, тангенс, котангенс — коротко о главном.

Синус угла — это отношение противолежащего (дальнего) катета к гипотенузе

Косинус угла — это отношение прилежащего (близкого) катета к гипотенузе

Тангенс угла — это отношение противолежащего (дальнего) катета к прилежащему (близкому)

Котангенс угла — это отношение прилежащего (близкого) катета к противолежащему (дальнему).

Понятие угла: радиан, градус

Давай для начала разберёмся в понятии угла.

Посмотрим на рисунок.

Вектор \( AB\) «повернулся» относительно точки \( A\) на некую величину. Так вот мерой этого поворота относительно начального положения и будет выступать угол \( \alpha \).

Что же ещё необходимо знать о понятии угла? Ну, конечно же, единицы измерения угла!

Угол, как в геометрии, так и в тригонометрии, может измеряться в градусах и радианах.

Углом в \( 1<>^\circ \) (один градус) называют центральный угол в окружности, опирающийся на круговую дугу, равную \( \frac<1><360>\) части окружности.

Таким образом, вся окружность состоит из \( 360\) «кусочков» круговых дуг. То есть угол, описываемый окружностью, равен \( 360<>^\circ \).

То есть на рисунке выше изображён угол \( \beta \), равный \( 50<>^\circ \), то есть этот угол опирается на круговую дугу размером \( \frac<50><360>\) длины окружности.

Углом в \( 1\) радиан называют центральный угол в окружности, опирающийся на круговую дугу, длина которой равна радиусу окружности.

Ну что, разобрался? Если нет, то давай разбираться по рисунку.

Итак, на рисунке изображён угол \( \gamma \), равный \( 1\) радиану.

То есть этот угол опирается на круговую дугу, длина которой равна радиусу окружности (длина \( AB\) равна длине \( BB’\) или радиус \( r\) равен длине дуги \( l\)).

Таким образом, длина дуги вычисляется по формуле:

\( l=\theta \cdot r\), где \( \theta \) — центральный угол в радианах.

Ну что, можешь, зная это, ответить, сколько радиан содержит угол, описываемый окружностью?

Да, для этого надо вспомнить формулу длины окружности. Вот она:

Ну вот, теперь соотнесём эти две формулы и получим, что угол, описываемый окружностью равен \( 2\pi \).

То есть, соотнеся величину в градусах и радианах, получаем, что \( 2\pi =360<>^\circ \).

Соответственно, \( \pi =180<>^\circ \).

Как можно заметить, в отличие от «градусов», слово «радиан» опускается, так как единица измерения обычно ясна из контекста.

А сколько радиан составляют \( 60<>^\circ \)?

Уловил? Тогда вперёд закреплять:

Тогда смотри ответы:

Cинус, косинус, тангенс, котангенс угла в прямоугольном треугольнике

Итак, с понятием угла разобрались. А что же всё-таки такое синус, косинус, тангенс, котангенс угла?

Давай разбираться. Для этого нам поможет прямоугольный треугольник.

Как называются стороны прямоугольного треугольника?

Всё верно, гипотенуза и катеты.

Гипотенуза — это сторона, которая лежит напротив прямого угла (в нашем примере это сторона \( AC\))

Катеты – это две оставшиеся стороны \( AB\) и \( BC\) (те, что прилегают к прямому углу).

Причём, если рассматривать катеты относительно угла \( \angle BAC\), то катет \( AB\) – это прилежащий катет, а катет \( BC\) — противолежащий.

Итак, теперь ответим на вопрос: что такое синус, косинус, тангенс и котангенс угла?

Синус угла – это отношение противолежащего (дальнего) катета к гипотенузе.

В нашем треугольнике \( \sin \beta =\frac\).

Косинус угла – это отношение прилежащего (близкого) катета к гипотенузе.

В нашем треугольнике \( \cos \beta =\frac\).

Тангенс угла – это отношение противолежащего (дальнего) катета к прилежащему (близкому).

В нашем треугольнике \( tg\beta =\frac\).

Котангенс угла – это отношение прилежащего (близкого) катета к противолежащему (дальнему).

В нашем треугольнике \( ctg\beta =\frac\).

Эти определения необходимо запомнить!

Чтобы было проще запомнить какой катет на что делить, необходимо чётко осознать, что в тангенсе и котангенсе сидят только катеты, а гипотенуза появляется только в синусе и косинусе.

А дальше можно придумать цепочку ассоциаций. К примеру, вот такую:

В первую очередь, необходимо запомнить, что синус, косинус, тангенс и котангенс как отношения сторон треугольника не зависят от длин этих сторон (при одном угле).

Тогда убедись, посмотрев на рисунок:

Рассмотрим, к примеру, косинус угла \( \beta \).

По определению, из треугольника \( ABC\): \( \cos \beta =\frac=\frac<4><6>=\frac<2><3>\).

Но ведь мы можем вычислить косинус угла \( \beta \) и из треугольника \( AHI\): \( \cos \beta =\frac=\frac<6><9>=\frac<2><3>\).

Видишь, длины у сторон разные, а значение косинуса одного угла одно и то же. Таким образом, значения синуса, косинуса, тангенса и котангенса зависят исключительно от величины угла.

Если разобрался в определениях, то вперёд закреплять их!

Тогда пробуй сам: посчитай то же самое для угла \( \beta \).

Ответы: \( \sin \ \beta =0,6;\ \cos \ \beta =0,8;\ tg\ \beta =0,75;\ ctg\ \beta =\frac<4><3>\).

Единичная (тригонометрическая) окружность

Разбираясь в понятиях градуса и радиана, мы рассматривали окружность с радиусом, равным \( 1\).

Такая окружность называется единичной. Еще ее называют тригонометрической. Это одно и тоже.

Эта окружность — универсальная шпаргалка для решения уравнений и даже неравенств, если уметь ей пользоваться!

У нас есть целая статья, посвященная ей, которая так и называется «Тригонометрическая (единичная) окружность».

Здесь мы тоже ее разберем довольно подробно.

Как можно заметить, данная окружность построена в декартовой системе координат.

Радиус окружности равен единице.

При этом центр окружности лежит в начале координат, начальное положение радиус-вектора зафиксировано вдоль положительного направления оси \( x\) (в нашем примере, это радиус \( AB\)).

Каждой точке окружности соответствуют два числа: координата по оси \( x\) и координата по оси \( y\).

А что это за числа-координаты? И вообще, какое отношение они имеют к рассматриваемой теме?

Для этого надо вспомнить про рассмотренный прямоугольный треугольник.

На рисунке, приведённом выше, можно заметить целых два прямоугольных треугольника.

Рассмотрим треугольник \( ACG\). Он прямоугольный, так как \( CG\) является перпендикуляром к оси \( x\).

Чему равен \( \cos \ \alpha \) из треугольника \( ACG\)?

Всё верно \( \cos \ \alpha =\frac\).

Кроме того, нам ведь известно, что \( AC\) – это радиус единичной окружности, а значит, \( AC=1\).

Подставим это значение в нашу формулу для косинуса. Вот что получается:

А чему равен \( \sin \ \alpha \) из треугольника \( ACG\)?

Ну конечно, \( \sin \alpha =\frac\)!

Подставим значение радиуса \( AC\) в эту формулу и получим:

Так, а можешь сказать, какие координаты имеет точка \( C\), принадлежащая окружности? Ну что, никак?

А если сообразить, что \( \cos \ \alpha \) и \( \sin \alpha \) — это просто числа?

Какой координате соответствует \( \cos \alpha \)?

Ну, конечно, координате \( x\)!

А какой координате соответствует \( \sin \alpha \)?

Всё верно, координате \( y\)!

Таким образом, точка \( C(x;y)=C(\cos \alpha ;\sin \alpha )\).

А чему тогда равны \( tg \alpha \) и \( ctg \alpha \)?

Всё верно, воспользуемся соответствующими определениями тангенса и котангенса и получим, что \( tg \alpha =\frac<\sin \alpha ><\cos \alpha >=\frac\), а \( ctg \alpha =\frac<\cos \alpha ><\sin \alpha >=\frac\).

А что, если угол будет больше \( 90<>^\circ =\frac<\pi ><2>\)?

Вот, к примеру, как на этом рисунке:

Что же изменилось в данном примере?

Давай разбираться. Для этого опять обратимся к прямоугольному треугольнику.

Всё верно, придерживаемся соответствующих определений тригонометрических функций:

Ну вот, как видишь, значение синуса угла всё так же соответствует координате \( y\); значение косинуса угла – координате \( x\); а значения тангенса и котангенса соответствующим соотношениям.

Таким образом, эти соотношения применимы к любым поворотам радиус-вектора.

Уже упоминалось, что начальное положение радиус-вектора – вдоль положительного направления оси \( x\).

До сих пор мы вращали этот вектор против часовой стрелки, а что будет, если повернуть его по часовой стрелке?

Ничего экстраординарного, получится так же угол определённой величины, но только он будет отрицательным.

Таким образом, при вращении радиус-вектора против часовой стрелки получаются положительные углы, а при вращении по часовой стрелке – отрицательные.

Итак, мы знаем, что целый оборот радиус-вектора по окружности составляет \( 360<>^\circ \) или \( 2\pi \).

В первом случае, \( 390<>^\circ =360<>^\circ +30<>^\circ \), таким образом, радиус-вектор совершит один полный оборот и остановится в положении \( 30<>^\circ \) или \( \frac<\pi ><6>\).

Таким образом, из приведённых примеров можем сделать вывод, что углы, отличающиеся на \( 360<>^\circ \cdot m\) или \( 2\pi \cdot m\) (где \( m\) – любое целое число), соответствуют одному и тому же положению радиус-вектора.

Ниже на рисунке изображён угол \( \beta =-60<>^\circ \).

Этот список можно продолжить до бесконечности.

Все эти углы можно записать общей формулой \( \beta +360<>^\circ \cdot m\) или \( \beta +2\pi \cdot m\) (где \( m\) – любое целое число)

Теперь, зная определения основных тригонометрических функций и используя единичную окружность, попробуй ответить, чему равны значения:

Вот тебе в помощь единичная окружность:

Возникли трудности? Тогда давай разбираться.

Отсюда мы определяем координаты точек, соответствующих определённым мерам угла.

Ну что же, начнём по порядку: углу в \( 90<>^\circ =\frac<\pi ><2>\) соответствует точка с координатами \( \left( 0;1 \right)\), следовательно:

\( \text\ 90<>^\circ =\frac=\frac<1><0>\Rightarrow \text\ 90<>^\circ \) — не существует;

Зная это, легко определить значения тригонометрических функций в соответствующих точках. Сначала попробуй сам, а потом сверяйся с ответами.

Ответы:

\( \displaystyle \sin \ 180<>^\circ =\sin \ \pi =0\) \( \displaystyle \cos \ 180<>^\circ =\cos \ \pi =-1\) \( \text\ 180<>^\circ =\text\ \pi =\frac<0><-1>=0\)

\( \text\ 180<>^\circ =\text\ \pi =\frac<-1><0>\Rightarrow \text\ \pi \) — не существует

\( \sin \ 270<>^\circ =-1\) \( \cos \ 270<>^\circ =0\)

\( \text\ 270<>^\circ =\frac<-1><0>\Rightarrow \text\ 270<>^\circ \) — не существует

\( \text\ 270<>^\circ =\frac<0><-1>=0\) \( \sin \ 360<>^\circ =0\) \( \cos \ 360<>^\circ =1\) \( \text\ 360<>^\circ =\frac<0><1>=0\)

\( \text\ 360<>^\circ =\frac<1><0>\Rightarrow \text\ 2\pi \) — не существует

\( \sin \ 450<>^\circ =\sin \ \left( 360<>^\circ +90<>^\circ \right)=\sin \ 90<>^\circ =1\) \( \cos \ 450<>^\circ =\cos \ \left( 360<>^\circ +90<>^\circ \right)=\cos \ 90<>^\circ =0\)

\( \text\ 450<>^\circ =\text\ \left( 360<>^\circ +90<>^\circ \right)=\text\ 90<>^\circ =\frac<1><0>\Rightarrow \text\ 450<>^\circ \) — не существует

\( \text\ 450<>^\circ =\text\left( 360<>^\circ +90<>^\circ \right)=\text\ 90<>^\circ =\frac<0><1>=0\).

Таким образом, мы можем составить следующую табличку:

Нет необходимости помнить все эти значения!

Достаточно помнить соответствие координат точек на единичной окружности и значений тригонометрических функций:

А вот значения тригонометрических функций углов в \( 30<>^\circ =\frac<\pi ><6>,\ 45<>^\circ =\frac<\pi ><4>\) и \( 30<>^\circ =\frac<\pi ><6>,\ 45<>^\circ =\frac<\pi ><4>\), приведённых ниже в таблице, необходимо запомнить:

Не надо пугаться, сейчас покажем один из примеров довольно простого запоминания соответствующих значений:

Источник

Что такое косинус

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Сегодня мы расскажем, что такое КОСИНУС.

Это слово, уверены, многим знакомо. Хотя бы потому что его проходят в школе. И многие наверняка точно определят, что это некий математический термин.

Но лишь единицы, которые действительно увлечены алгеброй и геометрией, вспомнят определение КОСИНУСА.

А между тем, без этих знаний не обойтись при сдаче ЕГЭ. Так что для старшеклассников это статья будет наиболее интересна. А для остальных – это хорошая возможность вспомнить подзабытые знания.

Со словом КОСИНУС школьники впервые знакомятся в 8 классе. И происходит это, когда проходят тему прямоугольных треугольников. Напомним, это такие треугольники, у которых две стороны пересекаются под прямым углом (90 градусов).

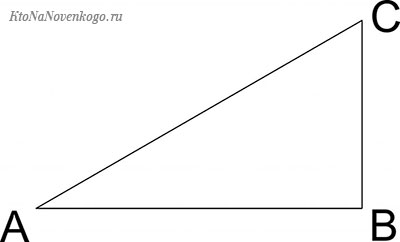
Выглядят они вот так:

У этого треугольника стороны АВ и ВС образуют между собой прямой угол. И напомним, по научному они называются КАТЕТАМИ. Этот термин имеет древнегреческие корни, произошло от «káthetos» и дословно переводится как «отвесный, опущенный, перпендикуляр».

А линия АС, которая соединяет два катета между собой, как многие знают из школьного курса, называется ГИПОТЕНУЗА. Этот термин также родом из Древней Греции. Слово «ὑποτείνουσα» переводится как «натянутая».

К чему мы так подробно это рассказали? Ну, во-первых, никогда не бывает лишним освежить в памяти старые знания. А во-вторых, это имеет непосредственное отношение к нашей теме.

Косинус – это отношения прилежащего катета к гипотенузе.

Так звучит официальное определение КОСИНУСА. Но у внимательных читателей может возникнуть вопрос, а что такое «прилежащий катет»? И к чему он собственно «прилегает»?

Вопрос правильный. Дело в том, что КОСИНУС имеет прямое отношение к углам. А точнее, является их тригонометрической функцией. И в данном случае, надо просто понимать, о каком угле идет речь.

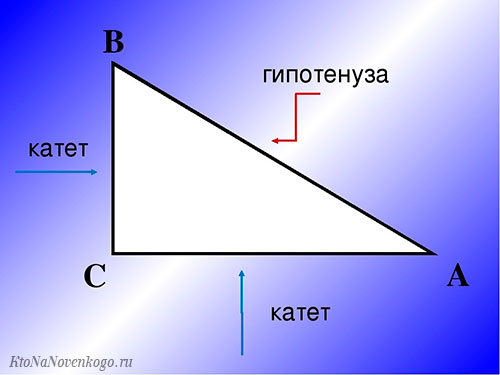
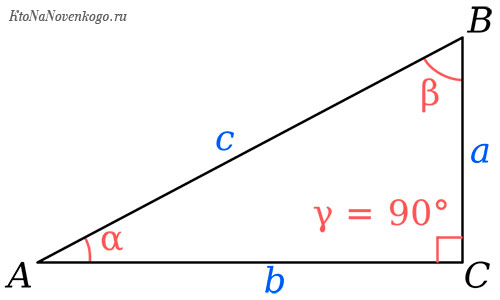
Вновь вернемся к нашему треугольнику АВС.

Если нам надо найти КОСИНУС угла с вершиной в точке А, то он будет равен отношению АВ (прилежащий катет) к АС (гипотенуза). А если нужно найти КОСИНУС угла с вершиной в точке С, то для него прилежащим катетом будет уже СВ, и уже его надо соотносить с гипотенузой АС.

Вот так это будет выглядеть более наглядно:

И если описывать формулы для конкретного примера, то выглядеть они будут так:

История изучения

Всегда интересно, откуда взялось то или иное слово. И как раз у КОСИНУСА это весьма интересная история. Она начинается еще в IV веке, и связана с именем индийского астронома и математика Ариабхты.

Он ввел специальный термин, которым называл дугу. Это было слово «ардхаджива», образованное от «ардха» (половина) и «джива» (тетива лука).

Спустя 500 лет уже арабские математики решили заменить этот сложный для их произношения термин на привычное себе слово «джайб». В переводе оно обозначало «выпуклость».

И наконец, еще немного позднее европейцы стали переводить арабские математические тексты и встретили этот термин. Для них слово «джайб» также было чужеродным, поэтому они заменили его на латинское «Sinus», что в переводе означает «кривизна, изгиб».

А вот слово КОСИНУС – это производное от СИНУС. Оно возникло от выражения «completely sinus», что в переводе означает «дополнительный синус» или «синус дополнительной дуги».

Фактически уже тогда математики установили главную зависимость между синусом и косинусом. И выражается она в следующей формуле:

Таблица косинусов

Для каждого угла можно найти и рассчитать свой косинус.

Приведем самые популярные значения:

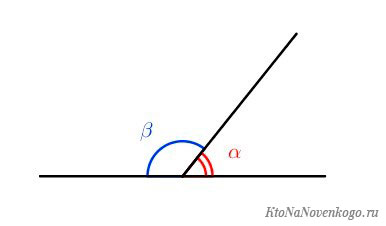
И еще одна важная зависимость. Если мы возьмем плоскость в 180 градусов:

В этом случае между углами α и β существует простая зависимость:

И тогда можно представить следующую формулу:

Данное утверждение будет верно при любых углах.

Вместо заключения

Есть еще две тригонометрические функции, которые широко используются в математике и изучаются в школе. Это ТАНГЕНС и КОТАНГЕНС.

Тангенс – это отношение противоположного катета к прилежащему. Также его можно представить как деление синуса на косинус.

Котангенс – это противоположная тангенсу функция, то есть отношение прилежащего катета к противолежащему. Или деление косинуса на синус.

Вот и все, что мы хотели рассказать про КОСИНУС.

Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru

Эта статья относится к рубрикам:

Комментарии и отзывы (1)

Да, хватило мучений с этими синусами и косинусами, а также со всякими аркатангисами в школе. Наверное, учительница просто не умела внятно объяснит, о чем идет речь. Но интересно не это. В Европе корчилась и потихоньку сходила на нет Римская империя, А некогда в не такой уж далекой Индии ученые мужи интересовались математикой и геометрией и придумывали новые термины.

Источник