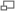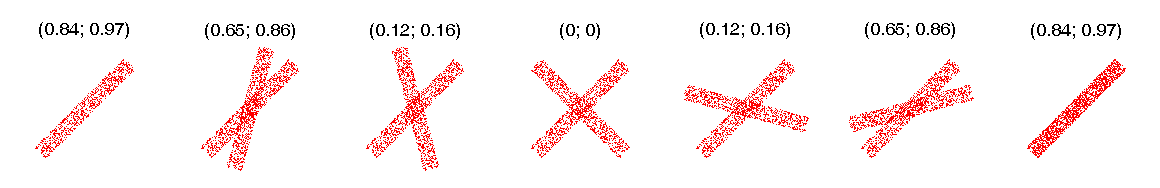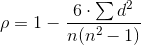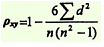Что такое корреляция спирмена
Коэффициент корреляции Спирмена
Материал из MachineLearning.
Содержание
Коэффициент корреляции Спирмена (Spearman rank correlation coefficient) — мера линейной связи между случайными величинами. Корреляция Спирмена является ранговой, то есть для оценки силы связи используются не численные значения, а соответствующие им ранги. Коэффициент инвариантен по отношению к любому монотонному преобразованию шкалы измерения.
Определение
Вычисление корреляции Спирмена:
Коэффициент корреляции Спирмена вычисляется по формуле:
Случай совпадающих наблюдений:
При наличии связок коэффициент корреляции Спирмена следует вычислять следующим образом:
Обоснование критерия Спирмена:
который наиболее удобен для вычислений.
Статистическая проверка наличия корреляции
Против альтернативы \ 0″ alt= «H_1:\; \rho\ >\ 0» />:
Рассмотрим центрированную и нормированную статистику Спирмена:
Нулевая гипотеза отвергается (против альтернативы — \ 0″ alt= «\left| \rho \right|\ >\ 0» />), если:
В 1978 году Р. Иман и У. Коновер предложили следующую поправку, значительно повышающую точность аппроксимации. Она использует линейную комбинацию нормальной и стьюдентовской квантилей. Положим:
Примеры
Направление линейной зависимости
Коэффициенты корреляции реагируют на изменение направления и зашумлённость линейной зависимости между переменными.
Наклон линейного тренда
Коэффициенты корреляции реагируют на изменение направления, но не реагируют на изменение наклона тренда. На первом, четвёртом и седьмом рисунках дисперсия одной из переменных близка к нулю, поэтому не удаётся зафиксировать факт линейной зависимости.
Нелинейная зависимость
Корреляции Кенделла и Спирмена не отражают меры нелинейной зависимости между переменными.
Линейная и нелинейная зависимости
На каждой из приведённых ниже иллюстраций осуществляется переход от линейной зависимости к нелинейной. Коэффициенты корреляции Кенделла и Спирмена реагируют на это одинаковым образом.
По мере смены линейной зависимости нелинейной значения коэффициентов корреляции падают.
Связь коэффициентов корреляции Спирмена и Пирсона
В случае выборок из нормального распределения коэффициент корреляции Спирмена может быть использован для оценки коэффициента корреляции Пирсона по формуле:
Связь коэффициентов корреляции Спирмена и Кенделла
Выборкам и соответствуют последовательности рангов:
Проведем операцию упорядочивания рангов.
Коэффициент корреляции Кенделла и коэффициент корреляции Спирмена выражаются через ранги следующим образом:
Утверждение. [1] Если выборки и не коррелируют (выполняется гипотеза ), то величины и сильно закоррелированы. Коэффициент корреляции между ними можно вычислить по формуле:
История
Критерий был предложен британским психологом Чарльзом Эдвардом Спирменом в 1904 году.
Что такое корреляция спирмена
Коэффициент корреляции рангов, предложенный К. Спирменом, относится к непараметрическим показателям связи между переменными, измеренными в ранговой шкале. При расчете этого коэффициента не требуется никаких предположений о характере распределений признаков в генеральной совокупности. Этот коэффициент определяет степень тесноты связи порядковых признаков, которые в этом случае представляют собой ранги сравниваемых величин.
— сумма квадратов разностей рангов.
Используя ранговый коэффициент корреляции, рассмотрим следующий пример.
Пример : Психолог выясняет, как связаны между собой индивидуальные показатели готовности к школе, полученные до начала обучения в школе у 11 первоклассников и их средняя успеваемость в конце учебного года.
Для решения этой задачи были проранжированы, во-первых, значения показателей школьной готовности, полученные при поступлении в школу, и, во-вторых, итоговые показатели успеваемости в конце года у этих же учащихся в среднем. Результаты представим в табл. 13.
| № учащихся | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| Ранги показателей школьной готовности | 3 | 5 | 6 | 1 | 4 | 11 | 9 | 2 | 8 | 7 | 10 |
| Ранги среднегодовой успеваемости | 2 | 7 | 8 | 3 | 4 | 6 | 11 | 1 | 10 | 5 | 9 |
| 1 | -2 | -2 | -2 | 0 | 5 | -2 | 1 | -2 | 2 | 1 | |
| 1 | 4 | 4 | 4 | 0 | 25 | 4 | 1 | 4 | 4 | 1 |
Подставляем полученные данные в формулу и производим расчет. Получаем:
Для нахождения уровня значимости обращаемся к табл. 20 приложения 6, в которой приведены критические значения для коэффициентов ранговой корреляции.
Подчеркнем, что в табл. 20 приложения 6, как и в таблице для линейной корреляции Пирсона, все величины коэффициентов корреляции даны по абсолютной величине. Поэтому, знак коэффициента корреляции учитывается только при его интерпретации.
Нахождение уровней значимости в данной таблице осуществляется по числу n, т. е. по числу испытуемых. В нашем случае n = 11. Для этого числа находим :
Строим соответствующую «ось значимости»:
При наличии одинаковых рангов формула расчета коэффициента линейной корреляции Спирмена будет несколько иной. В этом случае в формулу вычисления коэффициентов корреляции добавляются два новых члена, учитывающие одинаковые ранги. Они называются поправками на одинаковые ранги и добавляются в числитель расчетной формулы.
Если имеется две группы одинаковых рангов, в каком-либо столбце то формула поправки несколько усложняется:
Пример : Психолог, используя тест умственного развития (ШТУР) проводит исследование интеллекта у 12 учащихся 9 класса. Одновременно с этим, но просит учителей литературы и математики провести ранжирование этих же учащихся по показателям умственного развития. Задача заключается в том, чтобы определить, как связаны между собой объективные показатели умственного развития (данные ШТУРа) и экспертные оценки учителей.
Экспериментальные данные этой задачи и дополнительные столбцы, необходимые для расчета коэффициента корреляции Спирмена, представим в виде табл. 14.
| № учащихся | Ранги тестирования с помощью ШТУРа | Экспертные оценки учителей по математики | Экспертные оценки учителей по литературе | D (второго и третьего столбцов) | D (второго и четвертого столбцов) | (второго и третьего столбцов) | (второго и четвертого столбцов) |
| 1 | 6 | 5 | 5 | 1 | 1 | 1 | 1 |
| 2 | 7 | 10 | 8 | -3 | -1 | 9 | 1 |
| 3 | 4 | 8 | 7 | -4 | -3 | 16 | 9 |
| 4 | 5 | 4 | 11 | 1 | -6 | 1 | 36 |
| 5 | 9 | 6 | 3 | 3 | 6 | 9 | 36 |
| 6 | 12 | 8 | 6 | 4 | 6 | 16 | 36 |
| 7 | 2,5 | 2 | 11 | 0,5 | -8,5 | 0,25 | 77,25 |
| 8 | 2,5 | 3 | 11 | -0,5 | -8,5 | 0,25 | 77,25 |
| 9 | 10 | 8 | 1 | 2 | 9 | 4 | 81 |
| 10 | 8 | 11 | 3 | -3 | 5 | 9 | 25 |
| 11 | 11 | 12 | 3 | -1 | 8 | 1 | 64 |
| 12 | 1 | 1 | 9 | 0 | -8 | 0 | 64 |
| Суммы | 78 | 78 | 78 | 0 | 0 | 66,5 | 471,5 |
Проверяем по расчетной формуле. Проверка дает:
В пятом и шестом столбцах таблицы приведены величины разности рангов между экспертными оценками психолога по тесту ШТУР для каждого ученика и величинами экспертных оценок учителей, соответственно по математике и литературе. Сумма величин разностей рангов должна быть равна нулю. Суммирование величин D в пятом и шестом столбцах дало искомый результат. Следовательно, вычитание рангов проведено правильно. Подобную проверку необходимо делать каждый раз при проведении сложных видов ранжирования.
Прежде, чем начать расчет по формуле необходимо рассчитать поправки на одинаковые ранги для второго, третьего и четвертого столбцов таблицы.
В нашем случае во втором столбце таблицы два одинаковых ранга, следовательно, по формуле величина поправки D1 будет:
В третьем столбце три одинаковых ранга, следовательно, по формуле величина поправки D2 будет:
В четвертом столбце таблицы две группы по три одинаковых ранга, следовательно, по формуле величина поправки D3 будет:
Считаем первый ранговый коэффициент с учетом добавок по формуле. Получаем:
Подсчитаем без учета добавки:
Как видим, разница в величинах коэффициентов корреляции оказалась очень незначительной.
Считаем второй ранговый коэффициент с учетом добавок по формуле. Получаем:
Подсчитаем без учета добавки:
И опять, различия оказались очень незначительны. Поскольку число учащихся в обоих случаях одинаково, по табл. 20 приложения 6 находим критические значения при n = 12 сразу для обоих коэффициентов корреляции.
Откладываем первое значение на «оси значимости»:
В первом случае полученный коэффициент ранговой корреляции находится в зоне значимости. Поэтому психолог должен отклонить нулевую Н гипотезу о сходстве коэффициента корреляции с нулем и принять альтернативную Н о значимом отличии коэффициента корреляции от нуля. Иными словами, полученный результат говорит о том, что чем выше экспертные оценки учащихся по тесту ШТУР, тем выше их экспертные оценки по математике.
Откладываем второе значение на «оси значимости»:
Во втором случае коэффициент ранговой корреляции находится в зоне неопределенности. Поэтому психолог может принять нулевую Н гипотезу о сходстве коэффициента корреляции с нулем и отклонить альтернативную Н о значимом отличии коэффициента корреляции от нуля. В этом случае полученный результат говорит о том, что экспертные оценки учащихся по тесту ШТУР не связаны с экспертными оценками по литературе.
Для применения коэффициента корреляции Спирмена, необходимо соблюдать следующие условия:
1. Сравниваемые переменные должны быть получены в порядковой (ранговой) шкале, но могут быть измерены также в шкале интервалов и отношений.
2. Характер распределения коррелируемых величин не имеет значения.
3. Число варьирующих признаков в сравниваемых переменных X и Y должно быть одинаковым.
Таблицы для определения критических значений коэффициента корреляции Спирмена (табл. 20 приложение 6) рассчитаны от числа признаков равных n = 5 до n = 40 и при большем числе сравниваемых переменных следует использовать таблицу для пирсоновского коэффициента корреляции (табл. 19 приложение 6). Нахождение критических значений осуществляется при k = n.
Коэффициент корреляции Спирмена
Коэффициент корреляции Спирмена – статистический критерий, который наиболее часто используется при обработке эмпирических данных в курсовых, дипломных и магистерских работах по психологии. Этот критерий относится к типу непараметрических и не требует, чтобы данные были распределены по нормальному закону. Достаточно, если психологические показатели представлены в порядковой шкале, то есть учитывается только тот факт, что один показатель больше или меньше, чем другой.
Расчет коэффициента корреляции Спирмена
При проведении эмпирического исследования в дипломной по психологии для расчета коэффициента корреляции Спирмена удобнее пользоваться статистическими программами. Однако, этот критерий нетрудно рассчитать и вручную.
Пример расчета коэффициента корреляции Спирмена
Предположим, в рамках дипломной работы по психологии проводится исследование влияния климата в коллективе на состояние сотрудников. Одна из задач исследования состоит в выявлении взаимосвязи между климатом и эмоциональным истощением сотрудников.
В таблице приводятся данные, отражающие этапы расчета коэффициентов ранговой корреляции Спирмена. Суть расчета сводится к тому, что от собственно значений переходим к их рангам (ранг отражает положение показателя в общем списке и записывается в виде натурального числа). Далее находятся разности между рангами, эти разности возводятся в квадрат и суммируются.
Эмоциональное истощение (Х)
Психологический климат (Y)
Формула расчёта коэффициента корреляции Спирмена
D – разность между рангами
Сложность расчёта корреляций Спирмена вручную связана с необходимостью вводить поправки на одинаковые ранги, что достаточно трудоемко.
Сумма(D 2 )+Тх+ Тy 51,5+28+4,5
В специальной таблице находим значение критического значения коэффициента ранговой корреляции для выборки из 10 человек и для уровня значимости 0,05:
Следовательно, не существует связи между социально-психологическим климатом в коллективе и степенью истощения сотрудников. Для интерпретации данного результаты (а интерпретировать результаты статистических расчётов в дипломах по психологии очень важно) можно сказать следующее. Возможно, в коллективе сотрудников, где проводилось исследование, существуют социально-психологические или организационные факторы, которые опосредуют влияние климата в коллективе на эмоциональное истощение сотрудников. В связи с этим прямая взаимосвязь между этими показателями нивелируется.
Анализ результатов расчета коэффициентов ранговой корреляции Спирмена
Если коэффициент ранговой корреляции Спирмена вычисляется с помощью статистической программы, то она сама выделяет статистически значимые корреляции при заданном уровне статистической значимости (0,05 или 0,01).
Если расчёт коэффициента ранговой корреляции Спирмена проводится вручную, то после получения эмпирического значения его нужно сравнить с критическим. Критические значения коэффициентов ранговой корреляции Спирмена приводятся в специальных таблицах для разного объема выборки и уровня статистической значимости.
Далее нужно сравнить эмпирический и критический коэффициенты:
Несмотря на различные алгоритмы расчета корреляций Пирсона и Спирмена логика их анализа и интерпретации одинакова.
Различия коэффициентов корреляций Пирсона и Спирмена
На защите дипломных работ по психологии студента могут спросить о причинах, по которым он выбрал тот или иной тип коэффициента корреляции. То есть, важно понимать, чем принципиально различаются коэффициенты корреляции Пирсона и Спирмена.
Не вдаваясь в математические тонкости, можно сказать следующее:
Таким образом, в курсовых, дипломных и магистерских работах по психологии для анализа взаимосвязей между показателями лучше использовать коэффициенты ранговой корреляции Спирмена.
Библиотека постов MEDSTATISTIC об анализе медицинских данных
Ещё больше полезной информации в нашем блоге в Инстаграм @medstatistic
Критерии и методы
КРИТЕРИЙ СПИРМЕНА
– это непараметрический метод, который используется с целью статистического изучения связи между явлениями. В этом случае определяется фактическая степень параллелизма между двумя количественными рядами изучаемых признаков и дается оценка тесноты установленной связи с помощью количественно выраженного коэффициента.

1. История разработки коэффициента ранговой корреляции
Данный критерий был разработан и предложен для проведения корреляционного анализа в 1904 году Чарльзом Эдвардом Спирменом, английским психологом, профессором Лондонского и Честерфилдского университетов.
2. Для чего используется коэффициент Спирмена?
3. В каких случаях можно использовать коэффициент Спирмена?
В связи с тем, что коэффициент является методом непараметрического анализа, проверка на нормальность распределения не требуется.
Сопоставляемые показатели могут быть измерены как в непрерывной шкале (например, число эритроцитов в 1 мкл крови), так и в порядковой (например, баллы экспертной оценки от 1 до 5).
Эффективность и качество оценки методом Спирмена снижается, если разница между различными значениями какой-либо из измеряемых величин достаточно велика. Не рекомендуется использовать коэффициент Спирмена, если имеет место неравномерное распределение значений измеряемой величины.
4. Как рассчитать коэффициент Спирмена?
Расчет коэффициента ранговой корреляции Спирмена включает следующие этапы:
5. Как интерпретировать значение коэффициента Спирмена?
Также для оценки тесноты связи может использоваться шкала Чеддока:
| Абсолютное значение rxy | Теснота (сила) корреляционной связи |
| менее 0.3 | слабая |
| от 0.3 до 0.5 | умеренная |
| от 0.5 до 0.7 | заметная |
| от 0.7 до 0.9 | высокая |
| более 0.9 | весьма высокая |
Корреляционный анализ Спирмена
Описание метода ранговой корреляции Спирмена

Такие ряды могут представляться:
Метод предполагает проведение ранжирования показателей в отдельности для каждого из признаков.
Наименьшее значение имеет наименьший ранг.
Этот метод относится к непараметрическому статистическому методу, предназначенному для установления существования связи изучаемых явлений:
Корреляционный анализ
Статистический метод, предназначенный для выявления существования зависимости между 2 и более случайными величинами (переменными), а также ее силы, получил название корреляционного анализа.
Получил свое название от correlatio (лат.) – соотношение.
При его использовании возможны варианты развития событий:
В качестве инструментов используются различные меры связи (коэффициенты).
На их выбор оказывает влияние:
Корреляционная связь характеризуется такими признаками:
Цели корреляционного анализа
Корреляционный анализ не позволяет установить причинную зависимость между исследуемыми переменными.
Он проводится с целью:
Методы корреляционного анализа

Метод Пирсона применим для расчетов требующих точного определения силы, существующей между переменными. Изучаемые с его помощью признаки должны выражаться только количественно.
Для применения метода Спирмена или ранговой корреляции нет жестких требований в выражении признаков – оно может быть, как количественным, так и атрибутивным. Благодаря этому методу получается информация не о точном установлении силы связи, а имеющая ориентировочный характер.
В рядах переменных могут содержаться открытые варианты. Например, когда стаж работы выражается такими значениями, как до 1 года, более 5 лет и т.д.
Коэффициент корреляции
Наиболее распространены коэффициенты:
Ограничения использования коэффициента корреляции
Получение недостоверных данных при расчете коэффициента корреляции возможно в тех случаях, когда:
Проверка значимости корреляции
Для оценки статистических величин используется понятие их значимости или же достоверности, характеризующей вероятность случайного возникновения величины либо крайних ее значений.
Его значение сравнивается с табличным, количество степенней свободы принимается как 2. При получении расчетного значения критерия больше табличного, свидетельствует о значимости коэффициента корреляции.
При проведении экономических расчетов достаточным считается доверительный уровень 0,05 (95%) либо 0,01 (99%).
Ранги Спирмена
Коэффициент ранговой корреляции Спирмена позволяет статистически установить наличие связи между явлениями. Его расчет предполагает установление для каждого признака порядкового номера – ранга. Ранг может быть возрастающим либо убывающим.
Количество признаков, подвергаемых ранжированию, может быть любым. Это достаточно трудоемкий процесс, ограничивающий их количество. Затруднения начинаются при достижении 20 признаков.
Для расчета коэффициента Спирмена пользуются формулой:
n – отображает количество ранжируемых признаков;
d – не что иное как разность между рангами по двум переменным;
а ∑(d2) – сумма квадратов разностей рангов.
Применение корреляционного анализа в психологии
Статистическое сопровождение психологических исследований позволяет сделать их более объективными и высоко репрезентативными. Статистическая обработка данных полученных в ходе психологических экспериментов способствует извлечению максимума полезной информации.
Наиболее широкое применение в обработке их результатов получил корреляционный анализ.
Уместным является проведение корреляционного анализа результатов, полученных при проведении исследований:
Краткая инструкция к проведению корреляционного анализа по критерию Спирмена
Проведение корреляционного анализа с использованием метода Спирмена выполняется по следующему алгоритму:
Пример корреляции Спирмена
Необходимо установить наличие корреляционной связи между рабочим стажем и показателем травматизма при наличии следующих данных:
Наиболее подходящим методом анализа является ранговый метод, т.к. один из признаков представлен в виде открытых вариантов: рабочий стаж до 1 года и рабочий стаж 7 и более лет.
Решение задачи начинается с ранжирования данных, которые сводятся в рабочую таблицу и могут быть выполнены вручную, т.к. их объем не велик:
Отрицательное значение коэффициента свидетельствует о наличии обратной связи между признаками и позволяет утверждать, что небольшой стаж работы сопровождается большим числом травм. Причем, сила связи этих показателей достаточно большая.
Следующим этапом расчётов является определение достоверности полученного коэффициента:
• рассчитывается его ошибка и критерий Стьюдента