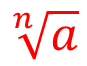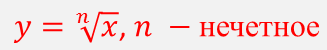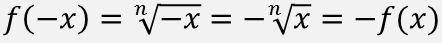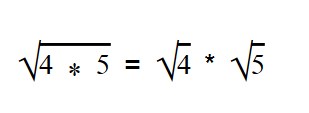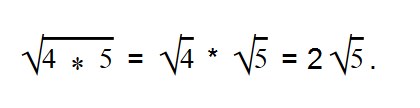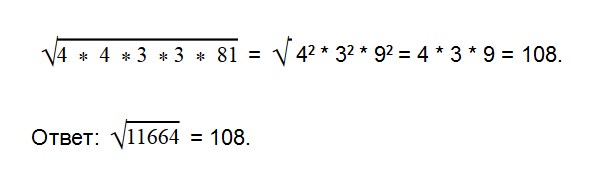Что такое корень функции
Корень
Корневая система и происхождение корней
Хорошо выражен, развит главный корень, выделяется на фоне остальных корней. Боковые и придаточные корни не выделяются, занимают по отношению к главному подчиненное положение. Характерна для двудольных растений: клевера, одуванчика лекарственного, лопуха большого.
Главный корень не развит или быстро отмирает, преобладают придаточные корни, растущие от побега. Корни равнозначны между собой. Мочковатая система характерна для большинства однодольных растений: лук репчатый, злаки. Для некоторых двудольных: подорожник большой, лютик едкий.
Можно отличить главный корень, он выделяется по размеру. Однако, хорошо развиты множественные придаточные и боковые корни. Смешанная корневая система характерна для клубники, земляники.
Зоны корня
Это зона представлена мелкими, быстро делящимися клетками верхушечной (апикальной) меристемы, расположенной на верхушке конуса нарастания. Такие молодые клетки особенно уязвимы, поэтому с целью защиты зону размножения покрывает корневой чехлик. Его клетки постоянно погибают от соприкосновения с почвой, образуя слизистый чехол, способствующий росту корня вглубь почвы и снижающий трение о почву.
Корневой чехлик у злаковых растений образуется из меристематических клеток, совокупность которых называется калиптрогеном. У двудольных растений имеется дерматокалиптроген, из которого помимо корневого чехлика развивается протодерма, из которой далее дифференцируется ризодерма (эпиблема).
Пикирование (пикировка) корня
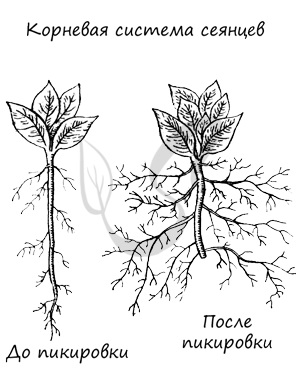
Это удаление верхушки главного корня вместе с зоной размножения. Таким образом садоводы останавливают рост главного корня и стимулируют развитие боковых и придаточных корней, корневая система получается разветвленной, и растение дает хороший урожай.
Корневое дыхание
Видоизменения корней
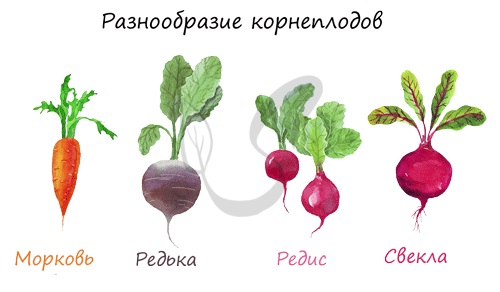
Запасающий орган, в котором складируется крахмал, сахароза, белки, клетчатка, минеральные соли. Формируется корнеплод из главного корня и основания стебля побега. Корнеплод характерен для двулетних растений: свеклы, петрушки, брюквы, моркови.
В первый год жизни у них формируется корнеплод с запасом питательных веществ, к осени надземная часть отмирает. Следующей весной растение «оживает» именно благодаря запасу веществ в корнеплоде с прошлого года. На второй год растения плодоносят и цветут, после чего отмирают полностью.
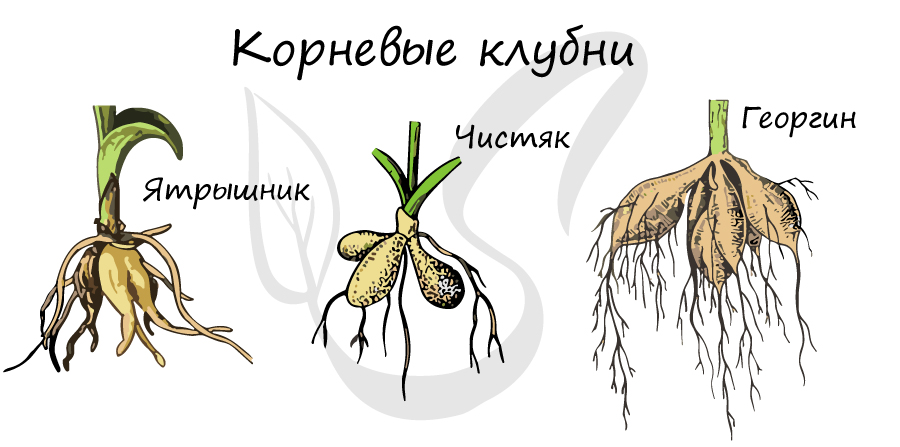
Представляют собой видоизменения боковых и придаточных корней. Выполняют запасающую функцию. Внешне утолщены и напоминают клубни. Имеются у чистяка, ятрышника, георгина, батата (сладкий картофель).
Некоторые растения образуют корни в воздушной среде. Воздушные корни встречаются у лиан и эпифитов, растущих в условиях тропиков, где воздух настолько влажный, что из него в буквальном смысле можно всасывать воду, что и делают воздушные корни. Многослойная покровная ткань воздушных корней подобно губке впитывает воду из влажного воздуха. Имеются у тропических папоротников, орхидеи, монстеры.
Слово эпифиты происходит от греч. ἐπι- — «на» и φυτόν — «растение», так обозначают растения, прикрепленные или произрастающие на других растениях, при этом совершенно не получающие от них питательных веществ, то есть явление паразитизма исключается.
Видоизмененные придаточные одревесневшие корни, растут на стволах и ветвях до почвы, у ее поверхности сильно разветвляются, тем самым «подпирая» растение. Придают опору растению и его ветвям, закрепляют его в почве. Встречаются у тропических растений: баньян, фикус.
Формируются у растений, произрастающих в воде или на болоте, в качестве механизма адаптации к недостаточному снабжению корней воздухом. Они приподнимаются над поверхностью воды и поглощают воздух. Такие корни имеет болотный кипарис (таксодиум).
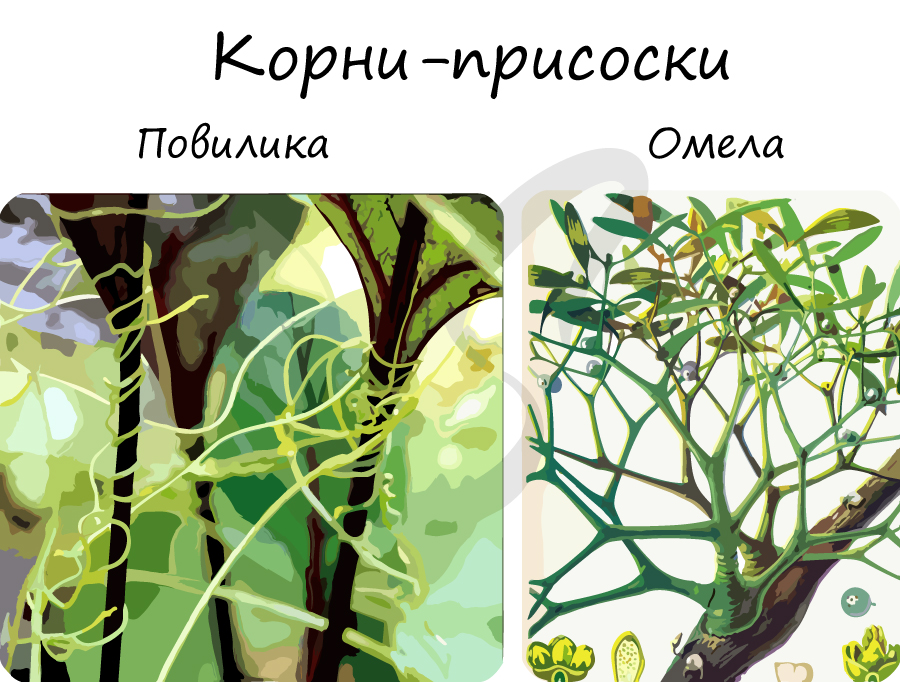
Видоизменения корней растений-паразитов, с помощью которых они высасывают питательные вещества из клеток растения-хозяина. Эти корни внедряются в стебли других растений и поглощают их соки: воду, растворенные в ней минеральные вещества, органические вещества. Имеются у повилики и заразихи. У омелы, погремка тоже имеются корни-присоски, но они всасывают только воду и растворенные в ней соли.
Бактериальные клубеньки представляют собой видоизмененные боковые корни, которые образуются в результате симбиоза растения и азотфиксирующих бактерий.
© Беллевич Юрий Сергеевич 2018-2021
Данная статья написана Беллевичем Юрием Сергеевичем и является его интеллектуальной собственностью. Копирование, распространение (в том числе путем копирования на другие сайты и ресурсы в Интернете) или любое иное использование информации и объектов без предварительного согласия правообладателя преследуется по закону. Для получения материалов статьи и разрешения их использования, обратитесь, пожалуйста, к Беллевичу Юрию.
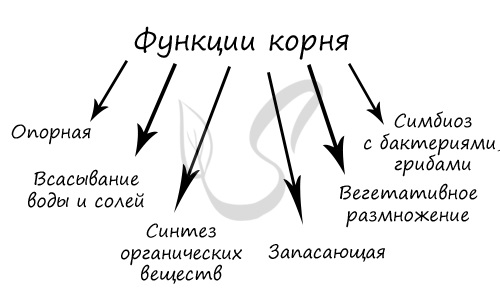
Функции корня.
Корнем n-степени из неотрицательного числа a является такое неотрицательное число, при возведении в n-степень которого получается число a.
Корнем нечетной n-степени из отрицательного числа a называется такое отрицательное число, при возведении в n-степень которого получается число a.
Где n – это показатель корня и a – подкоренное число.
Таким образом, извлечь корень любой степени (от второй и далее) можно из любого неотрицательного числа, а из отрицательного числа извлекается только корень нечетной степени.
На [0; +∞) можно поставить каждому числу х в соответствие единственное число корень n-степени из x при любом значении n.
То есть это означает, что на множестве [0; +∞) можно говорить о функции корня:
Теперь определим свойства данной функции и построим ее график.
Основные свойства функции:
Промежуток [0; +∞) – является областью определения.
Так как неотрицательное число является корнем n-степени из неотрицательного числа, значит промежуток [0; +∞) будет областью значения функции.
Поскольку симметричным множеством не является область определения функции, поэтому данная функция не является ни нечетной, ни четной.
Операция по извлечению корня вводилась как обратная операция возведения в соответствующую степень.
Значит можно утверждать, что:
Теперь можно построить график функции корня.
Пользуясь графиком, можно записать оставшиеся свойства функции.
На промежутке [0; +∞) функция возрастает.
На всей области определения функция выпукла вверх.
У функции наименьшим значением будет являться 0, а наибольшего значения она не имеет.
Если в каждой из точек некоторого промежутка функция дифференцируема, то это значит, что на данном промежутке она непрерывна.
В любой точке промежутка [0; +∞) существует эта производная, исключением является только точка 0. Поскольку в любой точке промежутка (0; +∞) функция имеет производную, значит на промежутке (0; +∞) функция дифференцируема.
Эти примеры касаются функции, у которой у равно корень n-степени из x, только при неотрицательных значениях аргумента.
Но если n является нечетным числом, то для отрицательных х также имеет смысл выражение корень n-степени из x. А значит, говорить можно о функции:
Запишем свойства данной функции.
Промежуток (– ∞; + ∞) является областью определения функции.
Промежуток (– ∞; + ∞) будет областью значений.
Область определения функции является симметричным множеством, значит данную функцию можно исследовать на четность:
Таким образом получаем, что функция будет нечетной при нечетном n.
Построим график функции.
Добавим к этой ветви еще ветвь, которая симметрична ей относительно начала координат, для этого воспользуемся свойством нечетности функции корня.
Еще несколько примеров графиков функции корня.
Что такое корень функции
Корень — осевой подземный орган растения, обладающий неограниченным концевым ростом.
Главный корень развивается из зародышевого корешка семени и играет в растении роль центральной оси подземной части.
Придаточные корни растут от побега.
Боковые корни образуются на главном и придаточных корнях.
Вся совокупность корней растения называется корневой системой.
типы корневых систем
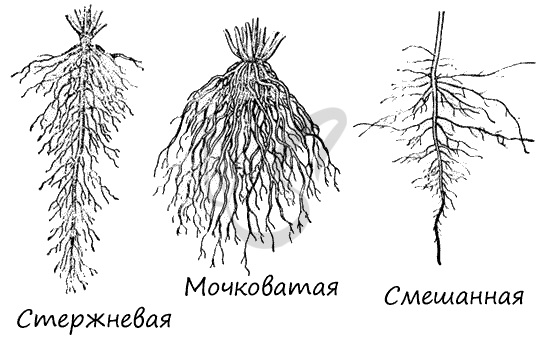
В зависимости от развития тех или иных видов корней выделяют два типа корневых систем (рис. 2). Стержневая корневая система состоит из хорошо развитого главного корня и отходящих от него более мелких боковых корней, которые в свою очередь делятся на боковые корни второго, третьего и т. д. порядков.
Такая корневая система характерна для двудольных растений и хорошо просматривается только у молодых растений, выращенных из семян. У старых многолетних растений главный корень со временем замедляет рост, а боковые корни догоняют его или даже перерастают.
Мочковатая корневая система состоит из многочисленных придаточных и боковых корней. Главный корень не развивается или развивается слабо.
Мочковатая корневая система характерна для однодольных растений.
Рис. 2. Типы корневых систем
внутреннее строение корня
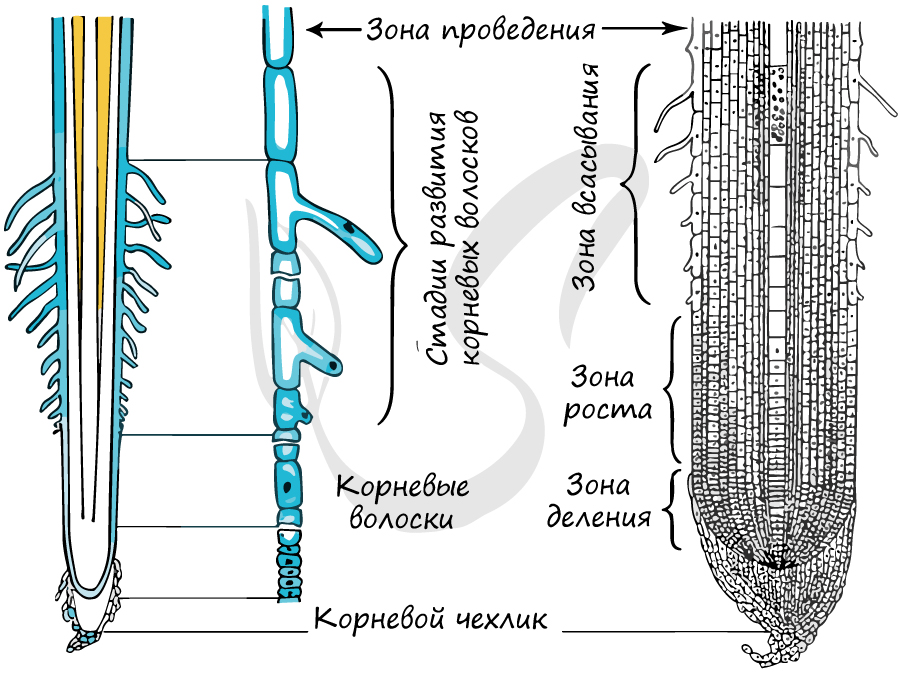
В строении корня различают несколько зон, каждая из которых имеет определенное строение и выполняет определенные функции (рис. 3).
Зона деления состоит из мелких постоянно делящихся клеток верхушечной меристемы. Это зона находится на кончиках всех корней растения. Благодаря верхушечной меристеме осуществляется рост корня в длину.
Корневой чехлик — несколько слоёв плотно сросшихся клеток с утолщенными стенками.
Функция корневого чехлика:
Клетки снаружи корневого чехлика постоянно разрушаются, а с внутренней стороны он нарастает благодаря клеткам меристемы.
Пикировка корня — удаление кончика главного корня — производится с целью прекращения роста главного корня и усиления роста боковых корней: общая площадь корневого питания увеличивается.
Зона растяжения (роста). В ней клетки растут, вытягиваясь в длину, благодаря чему и происходит удлинение корня.
В этой же зоне начинается дифференцировка клеток. Поверхностные клетки превращаются в клетки эпидермы. В центре формируются клетки проводящих тканей.
Зона всасывания. Зона всесывания снаружи покрыта тонкой покровной тканью эпиблемой (или ризодермой). В этой зоне клеткиэпиблемы образуют выросты — корневые волоски. Корневые волоски представляют собой длинные тонкие нитевидные клеточные выросты, в которые перемещается ядро клетки. По мере роста корня они разрушаются, эпидерма замещается пробкой и зона всасывания замещается зоной проведения.
Функция корневых волосков: поглощение из почвы воды и минеральных веществ.
Зона проведения продолжается до наземных частей растения. В ней находятся сосуды ксилемы, по которым от корня поднимается вода с минеральными веществами, и ситовидные трубки флоэмы, по которым в корень поступают органические вещества из листьев.
Корни подавляющего большинства растений выполняют шесть основных функций:
Поглощение воды и минеральных веществ корнем
Эта функция возникла у растений в связи с выходом на сушу.
Поглощение воды и минеральных веществ растением происходит независимо друг от друга, так как эти процессы основаны на различных механизмах действия. Вода проходит в клетки корня пассивно, а минеральные вещества поступают в клетки корня в основном в результате активного транспорта, идущего с затратами энергии.
Рис. 1. Горизонтальный транспорт воды:
1 — корневой волосок; 2 — апопластный путь; 3 — симпластный путь; 4 — эпиблема (ризодерма) 5 — эндодерма; 6 — перицикл; 7 — сосуды ксилемы; 8 — первичная кора; 9 — плазмодесмы; 10 — пояски Каспари.
Вода поступает в растение в основном по закону осмоса. Корневые волоски имеют огромную вакуоль с концентрированным клеточным соком, обладающую большим осмотическим потенциалом, который обеспечивает поступление воды из почвенного раствора в корневой волосок.
ГОРИЗОНТАЛЬНЫЙ ТРАНСПОРТ ВЕЩЕСТВ
Вода попадает в тело растения через ризодерму, поверхность которой сильно увеличена благодаря наличию корневых волосков.
В этой зоне в проводящем цилиндре корня формируется проводящая система корня — сосуды ксилемы, необходимая для обеспечения восходящего тока воды и минеральных веществ.
Вода с минеральными солями поглощается корневыми волосками. Эндодерма перекачивает эти вещества в проводящий цилиндр, создавая корневое давление и не позволяя воде выходить назад. Вода с солями поступает в сосуды проводящего цилиндра и поднимается транспирационным током по стеблю к листьям.
Горизонтальный транспорт воды и минеральных веществ происходит по трём путям (рис. 1):
В корне вода передвигается по межклетникам до эндодермы (апопластный путь). Здесь её дальнейшему продвижению мешают водонепроницаемые клеточные стенки, пропитанные суберином (пояски Каспари). Поэтому вода попадает в стелу по симпласту через пропускные клетки (вода проходит через плазматическую мембрану под контролем цитоплазмы пропускных клеток эндодермы). Благодаря этому происходит регуляция движения воды и минеральных веществ из почвы в ксилему. В стеле вода уже не встречает сопротивления и поступает в проводящие элементы ксилемы.
ВЕРТИКАЛЬНЫЙ ТРАНСПОРТ ВЕЩЕСТВ
Корни осуществляют проведение воды и минеральных веществ к наземным органам растения.
Вертикальное перемещение воды происходит по мёртвым клеткам ксилемы, которые не способны толкать воду к листьям. Это движение поддерживается транспирационной функцией листьев.
Корень представляет собой нижний концевой двигатель, подающий воду в сосуды стебля под давлением.
Корневое давление — сила, с которой корень нагнетает воду в стебель.
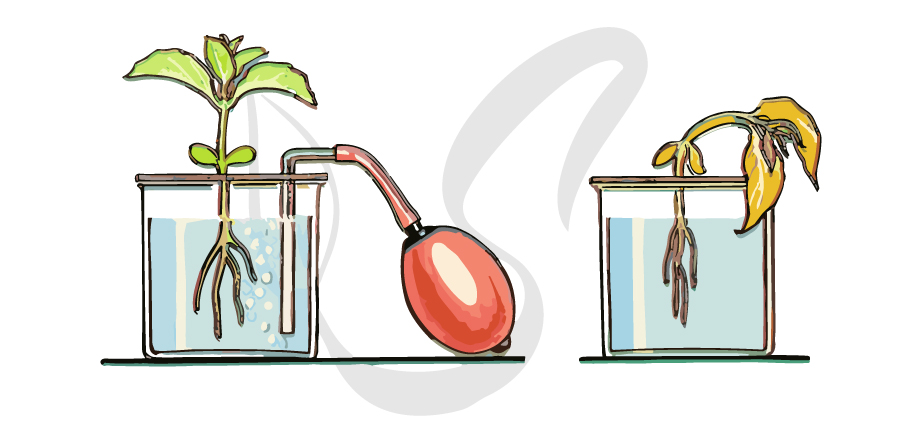
Корень активно перекачивает минеральные и органические вещества в сосуды ксилемы; в результате возникает повышенное осмотическое давление в сосудах корня относительно с давлением почвенного раствора. Величина корневого давления может достигать 3 атм. Доказательством наличия корневого давления служит, например, гуттация (выделение капелек воды листьями).
Верхний концевой двигатель, обеспечивающий вертикальный транспорт воды, возникает в результате транспирации (испарения воды с поверхности листьев).
При непрерывном испарении воды создаётся возможность для нового притока воды к листьям. Сосущая сила листьев у деревьев может достигать 20 атм.
В сосудах ксилемы вода движется в виде непрерывных водяных нитей. Молекулы воды движутся друг за другом за счет когезии (сцепления друг с другом) и адгезии (прилипания к стенкам сосудов).
Таким образом, поднятие воды по растению осуществляется благодаря верхнему и нижнему двигателям водного тока и силам сцепления молекул воды в сосудах. Основной движущей силой является транспирация.
ОСМОС И ТУРГОР
В живых клетках корня происходит первый отбор веществ, допускаемых внутрь растения. Участие живых клеток в принятии веществ обусловливает избирательную способность растения, благодаря которой различные вещества поглощаются в разных количествах. Так как поступление в сильной степени зависит от потребления, растение принимает на различных стадиях развития то одни соли, то другие. Чем сильнее развита корневая система, тем активнее идёт поглощение воды и солей.
Часто возникают ситуации, когда корни растений выполняют некоторые дополнительные функции или одна из основных функций требует большего развития. В таких случаях образуются видоизменения корней
Что такое квадратный корень
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Что такое квадратный корень
Определение арифметического квадратного корня ясности не добавляет, но заучить его стоит:
Арифметическим квадратным корнем из неотрицательного числа a называется такое неотрицательное число, квадрат которого равен a.
Определение квадратного корня также можно представить в виде формул:
√a = x
x 2 = a
x ≥ 0
a ≥ 0
Из определения следует, что a не может быть отрицательным числом. То есть то, что стоит под корнем — обязательно положительное число.
Чтобы разобраться, почему именно так и никак иначе, давайте рассмотрим пример.
Попробуем найти корень из √-16
Здесь логично предположить, что 4, но давайте проверим: 4*4 = 16 — не сходится.
Получается, что ни одно число не может дать отрицательный результат при возведении его в квадрат.
Числа, стоящие под знаком корня, должны быть положительными.
Исходя из определения, значение корня также не должно быть отрицательным.
Разница между квадратным корнем и арифметическим квадратным уравнением
Прежде всего, чтобы разграничить эти два понятия, запомните:
Это два нетождественных друг другу выражения.
Из выражения x 2 = 16 следует, что:
Если две вертикальные палочки возле x вводят вас в замешательство, почитайте нашу статью о модуле числа.
В то же самое время, из выражения x = √16 следует, что x = 4.
Если ситуация все еще кажется запутанной и нелогичной, просто запомните, что отрицательное число может быть решением только в квадратном уравнении. Если в решении «минус» — есть два варианта:
Если вы извлекаете квадратный корень из числа, то можете быть уверены, вас ждет «положительный» результат.
Давайте рассмотрим пример, чтобы окончательно выяснить разницу между квадратным корнем и квадратным уравнением.
Даны два выражения:
Первое выражение — квадратное уравнение.
Второе выражение — арифметический квадратный корень.
Мы видим, что результатом решения первого выражения стали два числа — отрицательное и положительное. А во втором случае — только положительное.
Запись иррациональных чисел с помощью квадратного корня
Иррациональное число — это число, которое нельзя представить в виде обыкновенной дроби.
Чаще всего, иррациональные числа можно встретить в виде корней, логарифмов, степеней и т.д.
Примеры иррациональных чисел:
Чтобы упростить запись иррациональных чисел, математики ввели понятие квадратного корня. Давайте разберем пару примеров, чтобы увидеть квадратный корень в деле.
Дано уравнение: x 2 = 2.
Сразу сталкиваемся с проблемой, поскольку очевидно, что ни одно целое число не подходит.
Переберем числа, чтобы удостовериться в этом:
1 * 1 = 1,
2 * 2 = 4,
3 * 3 = 9.
Отрицательные числа дают такой же результат. Значит результатом решения не могут быть целые числа.
Извлечение корней
Решать примеры с квадратными корнями намного легче, если запомнить как можно больше квадратов чисел. Для этого воспользуйтесь таблицей — сохраните ее себе и используйте для решения задачек.
Таблица квадратов
Вот несколько примеров извлечения корней, чтобы научиться пользоваться таблицей:
Ищем в таблице число 289, двигаемся от него влево и вверх, чтобы определить цифры, образующие нужное нам число.
Ищем в таблице число 3025.
Влево — 5, вверх — 5.
Ищем в таблице число 7396.
Ищем в таблице число 9025.
Ищем в таблице число 1600.
Извлечением корня называется нахождение его значение.
Свойства арифметического квадратного корня
У арифметического квадратного корня есть 3 свойства — их нужно запомнить, чтобы проще решать примеры.
Давайте потренируемся и порешаем примеры на все три операции с корнями. Не забывайте обращаться к таблице квадратов. Попробуйте решить примеры самостоятельно, а для проверки обращайтесь к ответам.
Умножение арифметических корней
Для умножения арифметических корней используйте формулу:
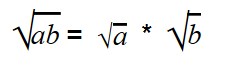 |
Примеры:
Внимательно посмотрите на второе выражение и запомните, как записываются такие примеры.
Если нет возможности извлечь корни из чисел, то поступаем так:
Деление арифметических корней
Для деления арифметических корней используйте формулу:
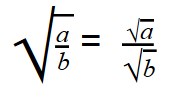 |
Примеры:
Выполняя деление, не забывайте сокращать множители. При делении арифметических корней, используйте правила преобразования обыкновенных дробей.
Возведение арифметических корней в степень
Для возведения арифметического корня в степень используйте формулу:
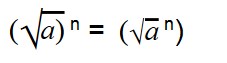 |
Примеры:
Эти две формулы нужно запомнить:
Повторите свойства степеней или запишитесь на курсы по математике, чтобы без труда решать такие примеры.
Внесение множителя под знак корня
Вы уже умеете по-всякому крутить и вертеть квадратными корнями: умножать, делить, возводить в степень. Богатый арсенал, не правда ли? Осталось овладеть еще парой приемов и можно без страха браться за любую задачку.
А теперь давайте разберемся, как вносить множитель под знак корня.
Число семь умножено на квадратный корень из числа девять.
Извлечем квадратный корень и умножим его на 7.
В данном выражение число 7 — множитель. Давайте внесем его под знак корня.
Запомните, что вносить множитель под знак корня обязательно нужно так, чтобы значение исходного выражения осталось неизменным. Иными словами, после наших манипуляций с корнем, значение выражения должно по-прежнему оставаться 21.
Вы помните, что (√a) 2 = a
Тогда число 7 должно быть возведено во вторую степень. В этом случае значение выражения останется тем же.
7√9 = √7 2 * 9 = √49 * 9 = √49 * √9 = 7 * 3 = 21.
Формула внесения множителя под знак корня:
Потренируемся вносить множители. Попробуйте решить примеры самостоятельно, сверяясь с ответами.
Вынесение множителя из-под знака корня
С тем, как вносить множитель под корень мы, кажется, разобрались. Но алгебра — такая алгебра, поэтому теперь неплохо бы и вынести множитель из-под знака корня.
Дано выражение в виде квадратного корня из произведения.
Вы уже наверняка без труда извлекаете квадратный корень из чего угодно, поэтому знаете, что делать.
Извлекаем корень из всех имеющихся множителей.
В данном выражении квадратный корень мы можем извлечь только из 4, поэтому:
Таким образом множитель выносится из-под знака корня.
Давайте разберем примеры. Попробуйте вынести множители из-под знака корня самостоятельно, сверяясь с ответами.
Раскладываем подкоренное выражение на множители 28 = 7*4.
Сравнение квадратных корней
Мы почти досконально разобрали арифметический квадратный корень, научились умножать, делить и возводить его в степень. Теперь вы без труда можете вносить множители под знак корня и выносить их оттуда. Осталось научиться сравнивать корни и стать непобедимым теоретиком.
Итак, чтобы понять, как сравнить два квадратных корня, нужно запомнить пару правил.
Если:
Потренируйтесь в сравнении корней. Сверяете свои результаты с ответами.
Ответ: преобразовываем выражение 9√5.
9√5 = √81 * √5 = √81*5 = √405
Ответ: преобразовываем выражение 7√12.
7√12 = √49 * √12 = √49*12 = √588
Это значит, что 7√12 > √20.
Как видите, ничего сложного в сравнении арифметических квадратных корней нет.
Самое главное — выучить формулы и сверяться с таблицей квадратов, если значения корня слишком большие для легкого вычисления в уме.
Не бойтесь пользоваться вспомогательными материалами. Математика просто создана для того, чтобы окружить себя подсказками и намеками.
Когда вы почувствуете, что уже достаточно натренировались в решении примеров с квадратными корнями, можете позволить себе время от времени прибегать к помощи онлайн-калькуляторов. Они помогут решать примеры быстрее и быть эффективнее.
Таких калькуляторов в интернете много, вот один из них.
Извлечение квадратного корня из большого числа
Вы уже наверняка познакомились и подружились с таблицей квадратов. Она — ваша правая рука. С ее помощью вы реактивно решаете примеры и, возможно, даже подумываете запомнить ее наизусть.
Но, как вы можете заметить, таблица заканчивается на числе 9801. А это, согласитесь, не самое крупное число из тех, что могут вам попасться в примере.
Чтобы извлечь корень из большого числа, которое отсутствует в таблице квадратов, нужно:
Извлечь корень из большого числа можно разными способами — вот один из них.
Извлечем корень из √2116.
Наша задача в том, чтобы определить между какими десятками стоит число 2116.
Мы видим что, 2116 больше 1600, но меньше 2500.
41, 42, 43, 44, 45, 46, 47, 48, 49.
Запомните лайфхак по вычислению всего на свете, что нужно возвести в квадрат.
Не секрет, что на последнем месте в любом числе может стоять только одна цифра от 1 до 0.
Как пользоваться таблицей
4 2 = 16 ⇒ 6
5 2 = 25 ⇒ 5
6 2 = 36 ⇒ 6
7 2 = 49 ⇒ 9
8 2 = 64 ⇒ 4
9 2 = 81 ⇒ 1
Мы знаем, что число 41, возведенное в квадрат, даст число, на конце которого — цифра 1.
Число, 42, возведенное в квадрат, даст число, на конце которого — цифра 4.
Число 43, возведенное в квадрат, даст число, на конце которого — 9.
Такая закономерность позволяет нам без записи «перебрать» все возможные варианты, исключая те, которые не дают нужную нам цифру 6 на конце.
Далее вычисляем: 44 * 44 = 1936.
Если такой способ показался не до конца понятным — можно потратить чуть больше времени и разложить число на множители. Если решить все правильно, получим такой же результат.
Еще пример. Извлечем корень из числа √11664
Разложим число 11664 на множители:
Запишем выражение в следующем виде:
Извлечь квадратный корень из большого числа гораздо проще с помощью калькулятора. Но знать парочку таких способов «на экстренный случай» точно не повредит. Например, для контрольной или ЕГЭ.
Чтобы закрепить все теоретические знания, давайте ещё немного поупражняемся в решении примеров на арифметические квадратные корни.
109004, Москва, ул. Александра Солженицына, 23а, строение 1, подъезд 10