Что такое контрольная сумма прошивки
Что такое контрольная сумма (КС) прошивки?
Добро пожаловать на ChipTuner Forum.
Опции темы
Что такое контрольная сумма (КС) прошивки?
Системы управления двигателем осуществляют самодиагностику функционирования датчиков и самого блока управления и его функциональных частей — ОЗУ, ПЗУ, ЕЕPROM. В простейшем случае, для такой проверки целостности «прошивки» внутри ее хранится контрольная сумма, которая получается суммированием байт прошивки. В прошивке контрольная сумма (КС) хранится вместе с собственным «зеркалом», то есть байтами, при сложении с которыми КС равна нулю. Это нужно для того, что бы само значение КС не влияло на результат вычисления КС программой ЭБУ. Программа ЭБУ при включении зажигания рассчитывает значение контрольной суммы и сравнивает это значение со значением, которое хранится в прошивке. Если эти значения не совпадают, то выстаяляется «Ошибка ПЗУ» и зажигается лампа индикации ошибок «Check Engine».
В более современном ПО применен двойной контроль КС ПЗУ, описанный выше и еще один алгоритм, не связанный с маской ошибок (в маске ошибок убрать ее нельзя), работающий параллельно с основным. Теоретически возможно одновременное применение любого количества проверок как всего содержимого ПЗУ, так и его частей.
Совсем недавно, прежде чем производить тюнинг какой-либо «прошивки» необходимо было разобраться с алгоритмом подсчета и расположением контрольной суммы в прошивке. Сейчас, при использовании специализированной программы редактирования калибровочных данных прошивок ChipTuning Pro и программатора Combiloader, все изменения КС, её подсчет и корректировка происходит автоматически и незаметно для пользователя. Мало того, эти программы позволяют установить и фиксировать любое произвольное отображение КС прошивки.
Что такое контрольная сумма прошивки
Сливать его оказалось достаточно просто для этого подсмотрев тут www.drive2.ru/l/3030227/ скачал все необходимое и понеслось :
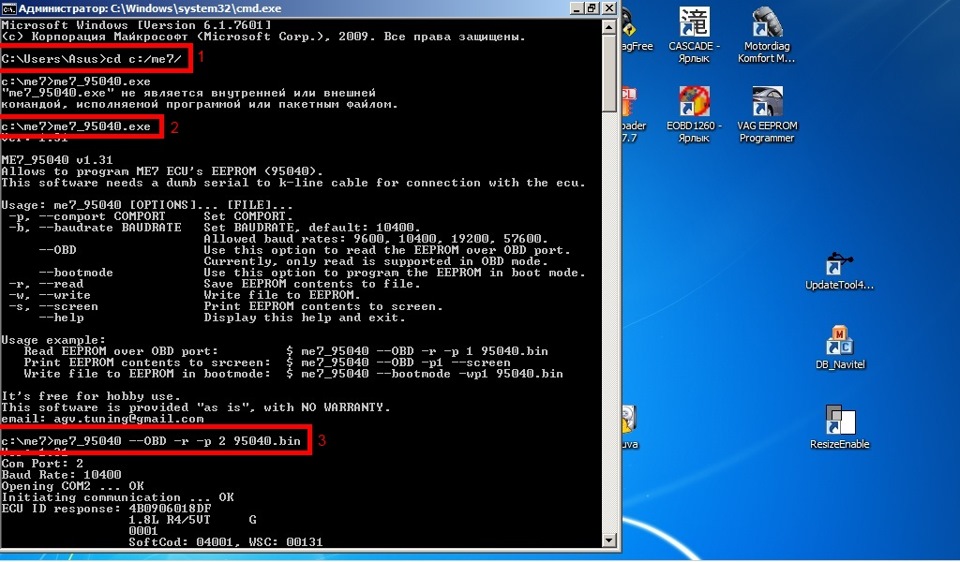
Качаем программу и ложим ее в папку «me7» на диск «C»
далее открываем командную строку, подключаем ноут к машине и пишем команды
cd c:/me7/ (переход в директорию программы)
me7_95040.exe (запуск программы)
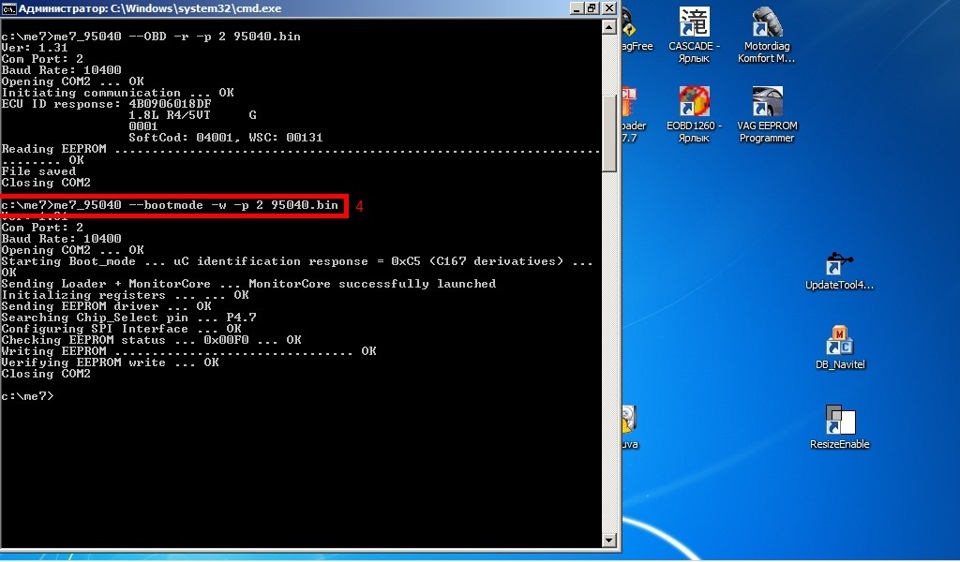
Где «2» перед «29040.bin» наш ком порт адаптера
Мануал по работе с еепром для любого Xeh редактора:
А о том как искать карты и строить из себя чип тюнера в следующей серии )))
Определимся сразу, что под термином «прошивка» в данной статье будет подразумеваться программное обеспечение электронного блока управления (ЭБУ) системы управления двигателем автомобиля. Что же содержится внутри прошивки? Условно области данных прошивки можно разбить на две области. Первая область – это сам программный код, который осуществляет управление работой автомобильного двигателя. Вторая область – это непосредственно калибр овочные данные (таблицы, графики, параметры) для работы программного кода.
При изготовлении тюнинговой прошивки в подавляющем большинстве случаев осуществляется изменение только калибровочных данных, а сам программный код никакому изменению не подвергается. Прежде всего это объясняется большой сложностью в изменении программного кода, а также тем, что в подавляющем большинстве случаев для изготовления тюнинговой прошивки достаточно изменения лишь калибровочных данных. Однако, случаи, когда необходимо вмешиваться в программный код прошивки все же встречаются, поэтому приведу один из примеров, когда без вмешательства в программный код для изготовления тюнинговой прошивки не обойтись. Например, при замене в системе управления двигателем датчика массового расхода воздуха (ДМРВ) на датчик абсолютного давления (ДАД) потребуется заново переписать алгоритм расчета количества воздуха, который попадает в цилиндры двигателя. Это объясняется тем, что алгоритмы для расчета количества воздуха при использовании ДМРВ и ДАД различны, и одним изменением калибровочных данных этот вопрос решить нельзя.
Современные системы управления двигателем осуществляют помимо самого управления, собственную самодиагностику. В число процедур самодиагностики, помимо прочих, входит и проверка исправности энергонезависимой памяти ЭБУ, которая содержит прошивку. Для такой проверки в прошивке хранится собственная контрольная сумма, которая получается суммированием байт определенной области прошивки (как области программного кода, так и калибровочных данных).
Программа ЭБУ в ходе своей работы рассчитывает значение контрольной суммы и сравнивает это значение со значением, которое хранится в прошивке (т.е. было заложено еще на заводе-изготовителе). Если эти значения не совпадают, то это считается ошибкой. У читателя в связи с эти может возникнуть вопрос: «Что же произойдет при изменении кем-либо, к примеру, калибровочных данных прошивки?». Ничего хорошего при этом не произойдет. В лучшем случае загорится лампа «Check Engine» в комбинации приборов, в худшем, автомобиль вообще не заведется. Естественно, контрольная сумма применяется не только для проверки исправности энергонезависимой памяти, а и для того, чтобы защитить саму прошивку (т.е. поставить преграду чип-тюнерам), от несанкционированного ее изменения.
Таким образом, прежде чем производить тюнинг какой-либо прошивки необходимо разобраться с алгоритмом подсчета и расположением контрольной суммы в теле прошивки, иначе грош цена такому чип-тюнингу. Данное положение не относится к специализированным программам редактирования калибровок прошивок, которые автоматически корректируют, контрольную сумму, после внесения пользователем изменений в калибровочные параметры.
Чтобы подытожить все вышесказанное, определим следующие положения:
Для просмотра нужна авторизация!
Для просмотра Вам необходимо авторизироваться.
Если Вы еще не зарегистрированы, перейдите по ссылке: Регистрация.
Парни выручайте нужно посчитать контрольную суммы для записи кессом
Авто
Toyota Land Cruiser 200 4.5 дизель 
Eprom. Подсчёт контрольной суммы
Наша строка 27 01 d8 7f 12 a1 c9 8f 75 75
Последние два байта это контрольная сумма. И при смене значений её нужно пересчитывать.
В расчет берется всё от 27 … до 8F.
Немного изменим запись чтоб было нагляднее понятно.
27 01 d8 7f 12 a1 89 8f B5 35
B5 — Первая контрольная сумма.
35 — Вторая контрольная сумма.
И так начнём.
Подсчёт первой КС по пунктам
1. Переводим каждое значение из 16-ой системы в 10-ую.
Пример: 27 01 d8 7f 12 a1 89 8f — 39 1 216 127 18 161 137 143
2. Нужно сложить все 8 байт в десятиричной системе.
Пример: 39+1+216+127+18+161+137+143=842
3. Переводим в 16 систему.
Пример: 842-034a
4. От результата нужно оставить только два правых символа
Пример: 034a — 4A
5. Далее переводим в 10-ую систему.
Пример: 4A = 74
6. От 255 нужно отнять результат пункта 5.
Пример: 255-74=181.
7. Переводим обратно в 16-ую систему. Это и будет КС 1
Пример: 181 в шестнадцатиричной системе будет b5
Итог: 1 Контрольная сумма B5.
Подсчёт 2 Контрольной суммы:
1. Берём опять эту строку 27 01 d8 7f 12 a1 89 8f.
2. Переводим каждый байт в двоичную систему.
Пример: 27 01 d8 7f 12 a1 89 8f — 00100111 00000001 11011000 01111111 00010010 10100001 10001001
10001111
3. Будем считать биты с лево на право для упрощения понимания.
Нужно сложить все первые биты каждого байта. Потом все вторые, потом третьи и так все 8.
Пример:0+0+1+0+0+1+1+1=4, вторые биты- 0+0+1+1+0+0+0+0=2 и т.д. с каждым битом.
Получим такое — 4,2,3,3,4,3,4,6.
4. Переписываем эту строчку в таком формате. Если число четное то=0, нечетное=1 и получаем байт в двоичной системе.
Пример:4,2,3,3,4,3,4,6.= 00110100
5. Переводим итог пункта 4 в Десятичную систему.
Пример: 00110100 = 52 (в десятичной).
6. Нужно прибавить единицу к результату пункта 5.
Пример: 52+1=53.
7. Переводим в Шестнадцатиричную систему. И получаем КС 2.
Пример: 53 = 35.
Вот и получилась вторая контрольная сумма. 35.
Делитесь своими наработками и давайте делиться уже со всеми бесплатно.
Спасибо God1983 и его другу за неоценимую помощь. Всем Добра!
Контрольная сумма: что это и почему это важно
Рассказываем на примере покупок в магазине.
Сегодня в вашем лексиконе появится важная новая фраза: контрольная сумма. Это инструмент опытных разработчиков, админов и хакеров, и сегодня он станет вашим.
Представьте ситуацию: вы приходите в магазин за наушниками. Находите нужные на витрине, пробуете их, вам всё нравится. Вы просите продавца принести такие же со склада, в упаковке.
Продавец приносит коробку, и вы понимаете, что вас хотят обмануть. Упаковку явно до этого вскрывали, в комплекте не все провода и накладки, плёночки сняты. Этими наушниками явно пользовались до вас.
Сотрудник говорит, что это ошибка в списке комплектности, а товар на самом деле новый, просто такой пришёл с завода. Вы ему не верите, отказываетесь от покупки и идёте в другой магазин. Там вы находите такие же наушники, проверяете и радуетесь, что купили нужную вещь.
В мире информации происходит почти то же самое: товар на складе — это какие-то данные, а список комплектности товара — это контрольная сумма, которая показывает, изменялись эти данные или нет. Если понимать, что это такое и как этим пользоваться, можно проверить подлинность файла и обезопасить себя от подделок, вирусов и шпионов.
Как это работает
На самом деле именно контрольной суммы уже нет — это название нам досталось с тех времён, когда для проверки точности передачи данных использовали 7 бит вместо 8. Восьмой бит был контрольным, и в нём находилась сумма первых семи бит без учёта старших разрядов. Когда получателю приходила очередная порция данных, он складывал 7 бит и сравнивал сумму с восьмым. Если они совпадали, значит, данные, скорее всего, передались верно. Тогда линии связи были не такими надёжными, как сейчас, и если что-то передавалось неправильно, такие данные нужно было отправить заново. С тех пор и пошло понятие контрольной суммы.
Сейчас сумму уже никто не использует, а вместо этого работают специальные программы:
Смысл технологии в том, что для любого файла и алгоритма есть только одна контрольная сумма. Если в файле изменить предложение, слово или несколько символов, контрольная сумма будет уже другой. Это как цифровой отпечаток пальца, только для данных.
Самый простой вариант организовать контрольную сумму — использовать хеши, например, MD5. Мы уже говорили про хеши в статье про Фейсбук и утерянные пароли, но MD5 — многогранная вещь, и в своё время его все использовали для создания контрольных сумм.
Но примерно с 2006 года все стали переходить на другие алгоритмы (CRC32, SHA-1, SHA-2 или MD5crypt). Дело в том, что уже есть методы, которые за приемлемое время могут взломать MD5-хеш и сделать другой файл с тем же размером и почти таким же содержимым, что и ваш. Это значит, что злоумышленник может подделать данные таким образом, что проверка контрольной суммы пройдёт успешно и вы будете думать, что всё в порядке.
Почему это важно
Если вы знаете контрольную сумму и алгоритм её нахождения, вы всегда можете проверить файл на целостность — скачался ли файл целиком и вообще тот ли это файл, что нужно.
Например, вы качаете новую прошивку на свой телефон. Если файл скачается неправильно, не до конца или с ошибками, во время перепрошивки телефон может сломаться, и восстановить его будет уже нельзя. Чтобы такого не было, производители прошивок прикладывают к файлам контрольную сумму, чтобы каждый мог проверить перед перепрошивкой, в порядке ли сам файл.
Чаще всего контрольную сумму используют разработчики ПО, которые выкладывают на своих страницах официальный софт и драйвера. Они говорят: ребята, вот файл, а вот его контрольная сумма. Если качаете у нас — проверьте, без ошибок ли вы скачали. А если качаете не у нас — сравните их контрольную сумму с нашей, вдруг они вам под видом драйвера хотят подсунуть какой-то вирус.
Простой расчет контрольной суммы
При передачи данных по линиям связи, используется контрольная сумма, рассчитанная по некоторому алгоритму. Алгоритм часто сложный, конечно, он обоснован математически, но очень уж неудобен при дефиците ресурсов, например при программировании микроконтроллеров.
Чтобы упростить алгоритм, без потери качества, нужно немного «битовой магии», что интересная тема сама по себе.
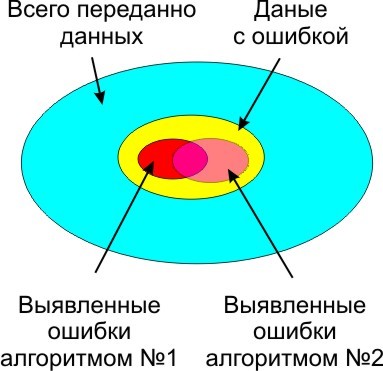
Без контрольной суммы, передавать данные опасно, так как помехи присутствуют везде и всегда, весь вопрос только в их вероятности возникновения и вызываемых ими побочных эффектах. В зависимости от условий и выбирается алгоритм выявления ошибок и количество данных в контрольной сумме. Сложнее алгоритм, и больше контрольная сумма, меньше не распознанных ошибок.
Причина помех на физическом уровне, при передаче данных.
Вот пример самого типичного алгоритма для микроконтроллера, ставшего, фактически, промышленным стандартом с 1979 года.
Не слабый такой код, есть вариант без таблицы, но более медленный (необходима побитовая обработка данных), в любом случае способный вынести мозг как программисту, так и микроконтроллеру. Не во всякий микроконтроллер алгоритм с таблицей влезет вообще.
Давайте разберем алгоритмы, которые вообще могут подтвердить целостность данных невысокой ценой.
Бит четности (1-битная контрольная сумма)
На первом месте простой бит четности. При необходимости формируется аппаратно, принцип простейший, и подробно расписан в википедии. Недостаток только один, пропускает двойные ошибки (и вообще четное число ошибок), когда четность всех бит не меняется. Можно использовать для сбора статистики о наличии ошибок в потоке передаваемых данных, но целостность данных не гарантирует, хотя и снижает вероятность пропущенной ошибки на 50% (зависит, конечно, от типа помех на линии, в данном случае подразумевается что число четных и нечетных сбоев равновероятно).
Для включения бита четности, часто и код никакой не нужен, просто указываем что UART должен задействовать бит четности. Типично, просто указываем:
Часто разработчики забывают даже, что UART имеет на борту возможность проверки бита четности. Кроме целостности передаваемых данных, это позволяет избежать устойчивого срыва синхронизации (например при передаче данных по радиоканалу), когда полезные данные могу случайно имитировать старт и стоп биты, а вместо данных на выходе буфера старт и стоп биты в случайном порядке.
8-битная контрольная сумма
Если контроля четности мало (а этого обычно мало), добавляется дополнительная контрольная сумма. Рассчитать контрольную сумму, можно как сумму ранее переданных байт, просто и логично
Естественно биты переполнения не учитываем, результат укладываем в выделенные под контрольную сумму 8 бит. Можно пропустить ошибку, если при случайном сбое один байт увеличится на некоторое значение, а другой байт уменьшится на то же значение. Контрольная сумма не изменится. Проведем эксперимент по передаче данных. Исходные данные такие:
.
,
на 256 отправленных телеграмм с ошибкой, одна пройдет проверку контрольной суммы. Смотрим статистику от виртуальной передачи данных, с помощью простой тестовой программы:
Или условный КПД=55%, от возможностей «идеальной» контрольной суммы. Такова плата за простоту алгоритма и скорость обработки данных. В целом, для многих применений, алгоритм работоспособен. Используется одна операция сложения и одна переменная 8-битовая. Нет возможности не корректной реализации. Поэтому алгоритм и применяется в контроллерах ADAMS, ICP, в составе протокола DCON (там дополнительно может быть включен бит четности, символы только ASCI, что так же способствует повышению надежности передачи данных и итоговая надежность несколько выше, так как часть ошибок выявляется по другим, дополнительным признакам, не связанных с контрольной суммой).
Не смотря на вероятность прохождения ошибки 1:143, вероятность обнаружения ошибки лучше, чем 1:256 невозможна теоретически. Потери в качестве работы есть, но не всегда это существенно. Если нужна надежность выше, нужно использовать контрольную сумму с большим числом бит. Или, иначе говоря, простая контрольная сумма, недостаточно эффективно использует примерно 0.75 бита из 8 имеющихся бит информации в контрольной сумме.
Для сравнения применим, вместо суммы, побитовое сложение XOR. Стало существенно хуже, вероятность обнаружения ошибки 1:67 или 26% от теоретического предела. Упрощенно, это можно объяснить тем, что XOR меняет при возникновении ошибке еще меньше бит в контрольной сумме, ниже отклик на единичный битовый сбой, и повторной ошибке более вероятно вернуть контрольную сумму в исходное состояние.
Так же можно утверждать, что контрольная сумма по XOR представляет из себя 8 независимых контрольных сумм из 1 бита. Вероятность того, что ошибка придется на один из 8 бит равна 1:8, вероятность двойного сбоя 1:64, что мы и наблюдаем, теоретическая величина совпала с экспериментальными данными.
Нам же нужен такой алгоритм, чтобы заменял при единичной ошибке максимальное количество бит в контрольной сумме. Но мы, в общей сложности, ограниченны сложностью алгоритма, и ресурсами в нашем распоряжении. Не во всех микроконтроллерах есть аппаратный блок расчета CRC. Но, практически везде, есть блок умножения. Рассчитаем контрольную сумму как произведение последовательности байт, на некоторую «магическую» константу:
Константа должна быть простой, и быть достаточно большой, для изменения большего числа бит после каждой операции, 211 вполне подходит, проверяем:
Всего 72% от теоретического предела, небольшое улучшение перед простой суммой. Алгоритм в таком виде не имеет смысла. В данном случае теряется важная информация из отбрасываемых старших 8..16 бит, а их необходимо учитывать. Проще всего, смешать функцией XOR с младшими битами 1..8. Приходим к еще более интенсивной модификации контрольной суммы, желательно с минимальным затратами ресурсов. Добавляем фокус из криптографических алгоритмов
Результат 91% от теоретического предела. Вполне годится для применения.
Если в микроконтроллере нет блока умножения, можно имитировать умножение операций сложения, смещения и XOR. Суть процесса такая же, модифицированный ошибкой бит, равномерно «распределяется» по остальным битам контрольной суммы.
На удивление хороший результат. Среднее значение 254,5 или 99% от теоретического предела, операций немного больше, но все они простые и не используется умножение.
Если для внутреннего хранения промежуточных значений контрольной суммы отдать 16 бит переменную (но передавать по линии связи будем только младшие 8 бит), что не проблема даже для самого слабого микроконтроллера, получим некоторое улучшение работы алгоритма. В целом экономить 8 бит нет особого смысла, и 8-битовая промежуточная переменная использовалась ранее просто для упрощения понимания работы алгоритма.
Что соответствует 100.6% от теоретического предела, вполне хороший результат для такого простого алгоритма из одной строчки:
Используется полноценное 16-битное умножение. Опять же не обошлось без магического числа 44111 (выбрано из общих соображений без перебора всего подмножества чисел). Более точно, константу имеет смысл подбирать, только определившись с предполагаемым типом ошибок в линии передачи данных.
Столь высокий результат объясняется тем, что 2 цикла умножения подряд, полностью перемешивают биты, что нам и требовалось. Исключением, похоже, является последний байт телеграммы, особенно его старшие биты, они не полностью замешиваются в контрольную сумму, но и вероятность того, что ошибка придется на них невелика, примерно 4%. Эта особенность практически ни как не проявляется статистически, по крайней мере на моем наборе тестовых данных и ошибке ограниченной 10 сбойными битами. Для исключения этой особенности можно делать N+1 итераций, добавив виртуальный байт в дополнение к имеющимся в тестовом блоке данных (но это усложнение алгоритма).
Вариант без умножения с аналогичным результатом. Переменная CRC 16-битная, данные 8-битные, результат работы алгоритма — младшие 8 бит найденной контрольной суммы:
Результат 100.6% от теоретического предела.
Вариант без умножения более простой, оставлен самый минимум функций, всего 3 математических операции:
Результат 86% от теоретического предела.
В этом случае потери старших бит нет, они возвращаются в младшую часть переменной через функцию XOR (битовый миксер).
Небольшое улучшение в некоторых случаях дает так же:
16-битная контрольная сумма
Далее, предположим что нам мало 8 бит для формирования контрольной суммы.
Следующий вариант 16 бит, и теоретическая вероятность ошибки переданных данных 1:65536, что намного лучше. Надежность растет по экспоненте. Но, как побочный эффект, растет количество вспомогательных данных, на примере нашей телеграммы, к 8 байтам полезной информации добавляется 2 байта контрольной суммы.
Простые алгоритмы суммы и XOR, применительно к 16-битной и последующим CRC не рассматриваем вообще, они практически не улучают качество работы, по сравнению с 8-битным вариантов.
Модифицируем алгоритм для обработки контрольной суммы разрядностью 16 бит, надо отметить, что тут так же есть магическое число 8 и 44111, значительное и необоснованное их изменение ухудшает работу алгоритма в разы.
Что соответствует 109% от теоретического предела. Присутствует ошибка измерений, но это простительно для 10 млн. итераций. Так же сказывается алгоритм создания, и вообще тип ошибок. Для более точного анализа, в любом случае нужно подстраивать условия под ошибки в конкретной линии передачи данных.
Дополнительно отмечу, что можно использовать 32-битные промежуточные переменные для накопления результата, а итоговую контрольную сумму использовать как младшие 16 бит. Во многих случаях, при любой разрядности контрольной суммы, так несколько улучшается качество работы алгоритма.
32-битная контрольная сумма
Перейдем к варианту 32-битной контрольной суммы. Появляется проблема со временем отводимым для анализа статистических данных, так как число переданных телеграмм уже сравнимо с 2^32. Алгоритм такой же, магические числа меняются в сторону увеличения
За 10 млн. итераций ошибка не обнаружена. Чтобы ускорить сбор статистики обрезал CRC до 24 бит:
Результат, из 10 млн. итераций ошибка обнаружена 3 раза
Вполне хороший результат и в целом близок к теоретическому пределу для 24 бит контрольной суммы (1:16777216). Тут надо отметить что функция контроля целостности данных равномерно распределена по всем битам CRC, и вполне возможно их отбрасывание с любой стороны, если есть ограничение на размер передаваемой CRC.
Для полноценных 32 бит, достаточно долго ждать результата, ошибок просто нет, за приемлемое время ожидания.
Вариант без умножения:
Сбоя для полноценной контрольной суммы дождаться не получилось. Контрольная сумма урезанная до 24 бит показывает примерно такие же результаты, 8 ошибок на 100 млн. итераций. Промежуточная переменная CRC 64-битная.
64-битная контрольная сумма
Ну и напоследок 64-битная контрольная сумма, максимальная контрольная сумма, которая имеет смысл при передачи данных на нижнем уровне:
Дождаться ошибки передачи данных, до конца существования вселенной, наверное не получится 🙂
Метод аналогичный тому, какой применили для CRC32 показал аналогичные результаты. Больше бит оставляем, выше надежность в полном соответствии с теоретическим пределом. Проверял на младших 20 и 24 битах, этого кажется вполне достаточным, для оценки качества работы алгоритма.
Так же можно применить для 128-битных чисел (и еще больших), главное подобрать корректно 128-битные магические константы. Но это уже явно не для микроконтроллеров, такие числа и компилятор не поддерживает.
Комментарии
В целом метод умножения похож на генерацию псевдослучайной последовательности, только с учетом полезных данных участвующих в процессе.
Рекомендую к использованию в микроконтроллерах, или для проверки целостности любых переданных данных. Вполне рабочий метод, уже как есть, не смотря на простоту алгоритма.
Мой проект по исследованию CRC на гитхаб.
Далее интересно было бы оптимизировать алгоритм на более реальных данных (не псевдослучайные числа по стандартному алгоритму), подобрать более подходящие магические числа под ряд задач и начальных условий, думаю можно еще выиграть доли процента по качеству работы алгоритма. Оптимизировать алгоритм по скорости, читаемости кода (простоте алгоритма), качеству работы. В идеале получить и протестировать образцы кода для всех типов микроконтроллеров, для этого как-раз и нужны примеры с использованием умножения 8, 16, 32 битных данных, и без умножения вообще.