Что такое констант в физике

Физическая константа

Фундамента́льная физи́ческая постоя́нная (вар.: конста́нта) — физическая величина, характеризующая не отдельные тела, а физические свойства нашего мира в целом. Фундаментальные физические постоянные возникают при математическом описании окружающего мира с помощью теоретической физики. Часто сюда же относят и некоторые другие физические постоянные, так или иначе связанные с конкретными телами.

Слово «постоянная» подразумевает, что численное значение этой величины не меняется со временем. В реальности это может быть и не так (например, в последние годы появились свидетельства в пользу того, что постоянная тонкой структуры меняется в ходе эволюции Вселенной). Однако даже если эти величины и меняются со временем, то крайне медленно, и сколько-нибудь заметные изменения стоит ожидать лишь на масштабах порядка возраста Вселенной.

Стоит различать размерные и безразмерные физические постоянные. Численное значение размерной величины зависит от выбора единиц измерения. Численное же значение безразмерных постоянных более фундаментально, так как оно не зависит от системы единиц.

Содержание

Фундаментальные физические постоянные

Размерные комбинации фундаментальных постоянных

Название	Символ	Значение	Прим.
планковская масса		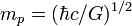2,176 44(11)×10 −8 кг	a
планковская длина		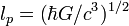1,616 252(81)×10 −35 м	a
планковское время		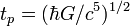5,391 24(27)×10 −44 с	a

Постоянные, связывающие разные системы единиц

Некоторые другие физические постоянные

Примечания

Ссылки

Полезное

Смотреть что такое «Физическая константа» в других словарях:

физическая константа — fizikinė konstanta statusas T sritis Standartizacija ir metrologija apibrėžtis Pastovus dydis, įeinantis į kurio nors fizikos dėsnio matematinę išraišką. atitikmenys: angl. physical constant vok. physikalische Konstante, f rus. физическая… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

Фундаментальная физическая константа — Фундаментальная физическая постоянная (вар.: константа) физическая величина, характеризующая не отдельные тела, а физические свойства нашего мира в целом. Фундаментальные физические постоянные возникают при математическом описании окружающего… … Википедия

Константа — Константа: Постоянная Математическая Физическая Константа (в программировании) Константа диссоциации кислоты Константа равновесия Константа скорости реакции Константа (Остаться в живых) См. также Констанция Констанций Константин Констант… … Википедия

Константа диссоциации — Константа диссоциации вид константы равновесия, которая показывает склонность большого объекта диссоциировать (разделяться) обратимым образом на маленькие объекты, как например когда комплекс распадается на составляющие молекулы, или когда… … Википедия

КОНСТАНТА ВЗАИМОДЕЙСТВИЯ — (константа связи) (от лат. constans постоянный) в квантовой теории поля (КТП) параметр, определяющий силу (интенсивность) взаимодействия частиц или полей. В общем виде К. в. задаётся как значение вершинной части (вершины) при определ. значениях… … Физическая энциклопедия

Константа автопротолиза — Константа автопротолиза физическая величина, характеризующая способность протонного растворителя к диссоциации. Обозначается KS. Является произведением концентраций иона лиония и иона лиата. Так, например, для растворителя, который… … Википедия

Константа равновесия — У этого термина существуют и другие значения, см. Константа. Для улучшения этой статьи желательно?: Проверить достоверность указанной в статье информации … Википедия

ФИЗИЧЕСКАЯ ХИМИЯ — раздел химии, в котором изучаются химические свойства веществ на основе физических свойств составляющих их атомов и молекул. Современная физическая химия широкая междисциплинарная область, граничащая с различными разделами физики, биофизики и… … Энциклопедия Кольера

Константа диссоциации кислоты — У этого термина существуют и другие значения, см. Константа. Константа диссоциации кислоты (Ka) константа равновесия реакции диссоциации кислоты на ион водорода и анион кислотного остатка. Для многоосновных кислот, диссоциация которых… … Википедия

Действие (физическая величина) — У этого термина существуют и другие значения, см. Действие (физика). Действие Размерность L2MT−1 Действие в физике скалярная физическая величина, являющаяс … Википедия

Источник

Физические константы

Фундамента́льная физи́ческая постоя́нная (вар.: конста́нта) — физическая величина, характеризующая не отдельные тела, а физические свойства нашего мира в целом. Фундаментальные физические постоянные возникают при математическом описании окружающего мира с помощью теоретической физики. Часто сюда же относят и некоторые другие физические постоянные, так или иначе связанные с конкретными телами.

Слово «постоянная» подразумевает, что численное значение этой величины не меняется со временем. В реальности это может быть и не так (например, в последние годы появились свидетельства в пользу того, что постоянная тонкой структуры меняется в ходе эволюции Вселенной). Однако даже если эти величины и меняются со временем, то крайне медленно, и сколько-нибудь заметные изменения стоит ожидать лишь на масштабах порядка возраста Вселенной.

Стоит различать размерные и безразмерные физические постоянные. Численное значение размерной величины зависит от выбора единиц измерения. Численное же значение безразмерных постоянных более фундаментально, так как оно не зависит от системы единиц.

Содержание

Фундаментальные физические постоянные

Размерные комбинации фундаментальных постоянных

Название	Символ	Значение	Прим.
планковская масса		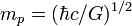2,176 44(11)×10 −8 кг	a
планковская длина		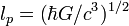1,616 252(81)×10 −35 м	a
планковское время		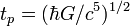5,391 24(27)×10 −44 с	a

Постоянные, связывающие разные системы единиц

Некоторые другие физические постоянные

Примечания

Ссылки

Полезное

Смотреть что такое «Физические константы» в других словарях:

ФИЗИЧЕСКИЕ КОНСТАНТЫ — (физические постоянные), постоянные величины, входящие в математические выражения физических законов (например, постоянная Авогадро). Физические константы, входящие в фундаментальные физические законы (например, всемирного тяготения закон) или… … Современная энциклопедия

ФИЗИЧЕСКИЕ КОНСТАНТЫ — (физические постоянные) постоянные величины, входящие в математические выражения физических законов (напр., газовая постоянная R в Клапейрона уравнении). Физические константы, входящие в фундаментальные физические законы (напр., закон всемирного… … Большой Энциклопедический словарь

Физические константы — (физические постоянные), постоянные величины, входящие в математические выражения физических законов (например, постоянная Авогадро). Физические константы, входящие в фундаментальные физические законы (например, всемирного тяготения закон) или… … Иллюстрированный энциклопедический словарь

ФИЗИЧЕСКИЕ КОНСТАНТЫ — см. Фундаментальные физические константы. Физическая энциклопедия. В 5 ти томах. М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988 … Физическая энциклопедия

физические константы — (физические постоянные), постоянные величины, входящие в математические выражения физических законов (например, газовая постоянная R в Клапейрона уравнении). Физические константы, входящие в фундаментальные физические законы (например, закон… … Энциклопедический словарь

физические константы — fizikinės konstantos statusas T sritis chemija apibrėžtis Pastovūs dydžiai, įeinantys į fizikos dėsnių matematines išraiškas. atitikmenys: angl. physical constants; universal constants rus. мировые константы; универсальные постоянные; физические… … Chemijos terminų aiškinamasis žodynas

ФИЗИЧЕСКИЕ КОНСТАНТЫ — (физические постоянные), пост. величины, входящие в матем. выражения физ. законов (напр., газ. постоянная R в Клапейрона уравнении). Ф. к., входящие в фундам. физ. законы (напр., закон всемирного тяготения) или являющиеся характеристиками частиц… … Естествознание. Энциклопедический словарь

Физические константы — то же, что Физические постоянные … Большая советская энциклопедия

Физические константы сложных виниловых эфиров — Виниловый эфир Температура кипения, °С/мм рт. ст. Плотность, г/см3 Показатель преломления, nD Винилформиат 46,6/760 0,9651* 1,4757* … Химический справочник

ФУНДАМЕНТАЛЬНЫЕ ФИЗИЧЕСКИЕ КОНСТАНТЫ — постоянные, входящие в ур ния, описывающие фундам. законы природы и свойства материи. Ф. ф. к. определяют точность, полноту и единство наших представлений об окружающем мире, возникая в теоретич. моделях наблюдаемых явлений в виде универсальных… … Физическая энциклопедия

Источник

Фундаментальные физические константы

Фундамента́льная физи́ческая постоя́нная (вар.: конста́нта) — физическая величина, характеризующая не отдельные тела, а физические свойства нашего мира в целом. Фундаментальные физические постоянные возникают при математическом описании окружающего мира с помощью теоретической физики. Часто сюда же относят и некоторые другие физические постоянные, так или иначе связанные с конкретными телами.

Слово «постоянная» подразумевает, что численное значение этой величины не меняется со временем. В реальности это может быть и не так (например, в последние годы появились свидетельства в пользу того, что постоянная тонкой структуры меняется в ходе эволюции Вселенной). Однако даже если эти величины и меняются со временем, то крайне медленно, и сколько-нибудь заметные изменения стоит ожидать лишь на масштабах порядка возраста Вселенной.

Стоит различать размерные и безразмерные физические постоянные. Численное значение размерной величины зависит от выбора единиц измерения. Численное же значение безразмерных постоянных более фундаментально, так как оно не зависит от системы единиц.

Содержание

Фундаментальные физические постоянные

Размерные комбинации фундаментальных постоянных

Название	Символ	Значение	Прим.
планковская масса		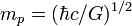2,176 44(11)×10 −8 кг	a
планковская длина		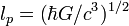1,616 252(81)×10 −35 м	a
планковское время		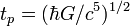5,391 24(27)×10 −44 с	a

Постоянные, связывающие разные системы единиц

Некоторые другие физические постоянные

Примечания

Ссылки

Полезное

Смотреть что такое «Фундаментальные физические константы» в других словарях:

ФУНДАМЕНТАЛЬНЫЕ ФИЗИЧЕСКИЕ КОНСТАНТЫ — постоянные, входящие в ур ния, описывающие фундам. законы природы и свойства материи. Ф. ф. к. определяют точность, полноту и единство наших представлений об окружающем мире, возникая в теоретич. моделях наблюдаемых явлений в виде универсальных… … Физическая энциклопедия

ФИЗИЧЕСКИЕ КОНСТАНТЫ — см. Фундаментальные физические константы. Физическая энциклопедия. В 5 ти томах. М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988 … Физическая энциклопедия

Фундаментальные физические постоянные — Для улучшения этой статьи желательно?: Викифицировать статью. Фундаментальные физические постоянные (вар.: ко … Википедия

ФИЗИЧЕСКИЕ КОНСТАНТЫ — (физические постоянные), постоянные величины, входящие в математические выражения физических законов (например, постоянная Авогадро). Физические константы, входящие в фундаментальные физические законы (например, всемирного тяготения закон) или… … Современная энциклопедия

ФИЗИЧЕСКИЕ КОНСТАНТЫ — (физические постоянные) постоянные величины, входящие в математические выражения физических законов (напр., газовая постоянная R в Клапейрона уравнении). Физические константы, входящие в фундаментальные физические законы (напр., закон всемирного… … Большой Энциклопедический словарь

Физические константы — (физические постоянные), постоянные величины, входящие в математические выражения физических законов (например, постоянная Авогадро). Физические константы, входящие в фундаментальные физические законы (например, всемирного тяготения закон) или… … Иллюстрированный энциклопедический словарь

физические константы — (физические постоянные), постоянные величины, входящие в математические выражения физических законов (например, газовая постоянная R в Клапейрона уравнении). Физические константы, входящие в фундаментальные физические законы (например, закон… … Энциклопедический словарь

Физические константы — Фундаментальная физическая постоянная (вар.: константа) физическая величина, характеризующая не отдельные тела, а физические свойства нашего мира в целом. Фундаментальные физические постоянные возникают при математическом описании окружающего… … Википедия

Физические постоянные — физические константы, фундаментальные постоянные, мировые постоянные, численные коэффициенты, входящие в уравнения физических законов и являющиеся в ряде случаев масштабными характеристиками физических процессов и микрообъектов. К Ф. п.… … Большая советская энциклопедия

Константы мировые — (см. Константа) они же фундаментальные мировые постоянные, физические константы, фундаментальные физические постоянные физические постоянные, входящие в фундаментальные физические законы (например закон всемирного тяготения) или являющиеся… … Начала современного естествознания

Источник

Физические константы

Смотреть что такое «Физические константы» в других словарях:

ФИЗИЧЕСКИЕ КОНСТАНТЫ — (физические постоянные), постоянные величины, входящие в математические выражения физических законов (например, постоянная Авогадро). Физические константы, входящие в фундаментальные физические законы (например, всемирного тяготения закон) или… … Современная энциклопедия

ФИЗИЧЕСКИЕ КОНСТАНТЫ — (физические постоянные) постоянные величины, входящие в математические выражения физических законов (напр., газовая постоянная R в Клапейрона уравнении). Физические константы, входящие в фундаментальные физические законы (напр., закон всемирного… … Большой Энциклопедический словарь

Физические константы — (физические постоянные), постоянные величины, входящие в математические выражения физических законов (например, постоянная Авогадро). Физические константы, входящие в фундаментальные физические законы (например, всемирного тяготения закон) или… … Иллюстрированный энциклопедический словарь

ФИЗИЧЕСКИЕ КОНСТАНТЫ — см. Фундаментальные физические константы. Физическая энциклопедия. В 5 ти томах. М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988 … Физическая энциклопедия

физические константы — (физические постоянные), постоянные величины, входящие в математические выражения физических законов (например, газовая постоянная R в Клапейрона уравнении). Физические константы, входящие в фундаментальные физические законы (например, закон… … Энциклопедический словарь

физические константы — fizikinės konstantos statusas T sritis chemija apibrėžtis Pastovūs dydžiai, įeinantys į fizikos dėsnių matematines išraiškas. atitikmenys: angl. physical constants; universal constants rus. мировые константы; универсальные постоянные; физические… … Chemijos terminų aiškinamasis žodynas

ФИЗИЧЕСКИЕ КОНСТАНТЫ — (физические постоянные), пост. величины, входящие в матем. выражения физ. законов (напр., газ. постоянная R в Клапейрона уравнении). Ф. к., входящие в фундам. физ. законы (напр., закон всемирного тяготения) или являющиеся характеристиками частиц… … Естествознание. Энциклопедический словарь

Физические константы — Фундаментальная физическая постоянная (вар.: константа) физическая величина, характеризующая не отдельные тела, а физические свойства нашего мира в целом. Фундаментальные физические постоянные возникают при математическом описании окружающего… … Википедия

Физические константы сложных виниловых эфиров — Виниловый эфир Температура кипения, °С/мм рт. ст. Плотность, г/см3 Показатель преломления, nD Винилформиат 46,6/760 0,9651* 1,4757* … Химический справочник

ФУНДАМЕНТАЛЬНЫЕ ФИЗИЧЕСКИЕ КОНСТАНТЫ — постоянные, входящие в ур ния, описывающие фундам. законы природы и свойства материи. Ф. ф. к. определяют точность, полноту и единство наших представлений об окружающем мире, возникая в теоретич. моделях наблюдаемых явлений в виде универсальных… … Физическая энциклопедия

Источник

ФИЗИЧЕСКИЕ КОНСТАНТЫ

(физические постоянные), пост. величины, входящие в матем. выражения физ. законов (напр., газ. постоянная R в Клапейрона уравнении). Ф. к., входящие в фундам. физ. законы (напр., закон всемирного тяготения) или являющиеся характеристиками частиц и процессов микромира, наз. фундаментальными, универсальными или мировыми Ф. к. (таковы гравитац. постоянная, постоянная Планка, скорость света и др.). Ф. к. определяют экспериментально или вычисляют с макс. точностью, что необходимо для количеств. исследований физ. явлений и проверки физ. теорий.

Смотреть что такое «ФИЗИЧЕСКИЕ КОНСТАНТЫ» в других словарях:

ФИЗИЧЕСКИЕ КОНСТАНТЫ — (физические постоянные), постоянные величины, входящие в математические выражения физических законов (например, постоянная Авогадро). Физические константы, входящие в фундаментальные физические законы (например, всемирного тяготения закон) или… … Современная энциклопедия

ФИЗИЧЕСКИЕ КОНСТАНТЫ — (физические постоянные) постоянные величины, входящие в математические выражения физических законов (напр., газовая постоянная R в Клапейрона уравнении). Физические константы, входящие в фундаментальные физические законы (напр., закон всемирного… … Большой Энциклопедический словарь

Физические константы — (физические постоянные), постоянные величины, входящие в математические выражения физических законов (например, постоянная Авогадро). Физические константы, входящие в фундаментальные физические законы (например, всемирного тяготения закон) или… … Иллюстрированный энциклопедический словарь

ФИЗИЧЕСКИЕ КОНСТАНТЫ — см. Фундаментальные физические константы. Физическая энциклопедия. В 5 ти томах. М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988 … Физическая энциклопедия

физические константы — (физические постоянные), постоянные величины, входящие в математические выражения физических законов (например, газовая постоянная R в Клапейрона уравнении). Физические константы, входящие в фундаментальные физические законы (например, закон… … Энциклопедический словарь

физические константы — fizikinės konstantos statusas T sritis chemija apibrėžtis Pastovūs dydžiai, įeinantys į fizikos dėsnių matematines išraiškas. atitikmenys: angl. physical constants; universal constants rus. мировые константы; универсальные постоянные; физические… … Chemijos terminų aiškinamasis žodynas

Физические константы — Фундаментальная физическая постоянная (вар.: константа) физическая величина, характеризующая не отдельные тела, а физические свойства нашего мира в целом. Фундаментальные физические постоянные возникают при математическом описании окружающего… … Википедия

Физические константы — то же, что Физические постоянные … Большая советская энциклопедия

Физические константы сложных виниловых эфиров — Виниловый эфир Температура кипения, °С/мм рт. ст. Плотность, г/см3 Показатель преломления, nD Винилформиат 46,6/760 0,9651* 1,4757* … Химический справочник

ФУНДАМЕНТАЛЬНЫЕ ФИЗИЧЕСКИЕ КОНСТАНТЫ — постоянные, входящие в ур ния, описывающие фундам. законы природы и свойства материи. Ф. ф. к. определяют точность, полноту и единство наших представлений об окружающем мире, возникая в теоретич. моделях наблюдаемых явлений в виде универсальных… … Физическая энциклопедия

Источник