Что такое комплексно сопряженные числа
Комплексно-сопряженные числа
Что такое комплексно-сопряженные числа? Как комплексно-сопряженные числа изображаются на комплексной плоскости?
у которых действительные части равны, а коэффициенты при мнимой части — противоположные числа, называются комплексно-сопряженными.
(другими словами, комплексонов-сопряженные числа — это комплексные числа, которые отличаются только знаком при мнимой части).
Примеры комплексно-сопряженных чисел:
Свойства комплексно сопряженных чисел
1) Действительное число является комплексно-сопряженным самому себе, так как a+0i=a-0i.
2) Сумма комплексно- сопряженных чисел — действительное число:
3) Разность комплексно-сопряженных чисел — мнимое число:
4) Произведение комплексно-сопряженных чисел — действительное число:
Изображение комплексно-сопряженных чисел на плоскости
На комплексной плоскости z1=a+bi и z2=a-bi изображаются
1) точками, симметричными относительно действительной оси ox.
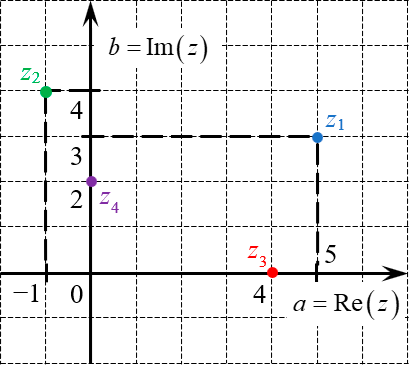
Например, z1= — 6+3i и z2= — 6-3i; z3=0+2i и z4=0-2i; z5=5+0i и z6=5-0i.
2) векторами, симметричными относительно действительной оси ox.
Например, z1= 0+4i и z2= 0-4i; z3= 5+2i и z4= 5-2i; z5= — 6+0i и z6=- 6-0i.
Что такое комплексные числа
Первый урок по комплексным числам. Сегодня мы разберём:
Если же вас интересует тригонометрическая форма записи комплексного числа, либо извлечение корней из комплексных чисел — этим темам посвящены отдельные уроки.
Сегодня — лишь самое главное. Но не самое простое.:)
0. Краткая вводная
Когда-то нам хватало натуральных чисел:
Всё было прекрасно: «У тебя 5 бананов, у меня ещё 3 — итого у нас 5 + 3 = 8 бананов». Сумма двух натуральных чисел всегда даёт новое натуральное число (говорят, что операция сложения замкнута на множестве натуральных чисел).
Но вот на сцену выходит вычитание — и натуральных чисел стало недостаточно. Например разность 3 − 5 = −2 уже не будет натуральным. Так появились целые числа (натуральные, им противоположные и ноль):
Дальше к делу подключились операции умножения и деления. Да, произведение двух целых чисел всё ещё целое, но вот деление приводит к образованию дробей. Например, 1 : 2 или 5 : 4 уже нельзя записать целым числом. Так появилось множество рациональных чисел или множество дробей:
Это был настоящий триумф для древней математики, и в тот момент казалось, что ничего больше уже изобрести нельзя. Да и зачем?
Проблема пришла откуда не ждали. В какой-то момент классическое умножение «разрослось» до возведения в степень:
Тут-то и выяснилось, что возведение рационального числа в натуральную степень всё ещё будет рациональным числом. Но вот обратная операция — извлечение корня — выносит нас за пределы рациональных чисел:
\[\sqrt<2>=1,41421. \notin \mathbb\]
Так появилось множество действительных чисел — множество бесконечных десятичных дробей, которые могут быть периодическими (и тогда это обычное рациональное число) и непериодическими (такие числа называют иррациональными, и их неизмеримо больше).
Казалось бы: ну вот теперь точно всё! Что ещё нужно для счастья? Проблема в том, что на множестве действительных чисел нельзя извлечь даже самый простой квадратный корень из отрицательного числа:
Однако законы физики (особенно электродинамика и вообще всё, где есть слово «динамика») как бы намекали, что множество содержательных процессов протекает там, где привычные корни не извлекаются. А значит, следует расширить множество действительных чисел так, чтобы такие корни всё же извлекать.
И тут открылись врата в Ад.
1. Комплексная единица
Начнём с ключевого определения.
Однако в остальном это такое же число, как и все остальные. Комплексные единицы можно складывать, умножать, их можно комбинировать с «нормальными» числами:
2. Стандартная форма записи комплексных чисел
А теперь всё по-взрослому.
Определение. Комплексное число — это любое число вида
\[\begin
\[\begin
И напротив: существуют «чисто мнимые» числа, у которых вообще нет действительной части. Та же комплексная единица, например:
\[\begin
Таким образом, действительные числа являются частным случаем комплексных. Подобно тому как рациональные числа являются частным случаем действительных (в конце концов, рациональные числа — те же десятичные дроби, но с дополнительным условием: они периодические).
2.1. Равенство комплексных чисел
В самом деле, пусть некоторое число записано двумя способами:
Соберём все действительные слагаемые слева, а мнимые — справа:
Слева мы видим действительное число. Значит, справа тоже должно стоять действительное число. Единственная ситуация, в которой это возможно:
Получается, что справа от знака равенства стоит ноль. Следовательно, слева тоже ноль:
Следовательно, исходные записи совпадают.
Поэтому имеет смысл следующее определение.
Определение. Два комплексных числа равны друг другу тогда и только тогда, когда равны их действительные части, а также равны их мнимые части:
Если хотя бы одна из частей не равна, то и сами числа не равны.
Поскольку от перестановки слагаемых сумма не меняется (сложение чисел — настолько суровая операция, что какие-то там «комплексные единицы» никак не нарушают его коммутативности), мы можем записать:
А вот перестановка мнимой и действительной части (если эти части разные) немедленно ведёт к нарушению равенства:
К координатной плоскости мы ещё вернёмся. А пока определим правила сложения и вычитания комплексных чисел.
3. Сложение и вычитание комплексных чисел
Выше мы проводили аналогию между комплексными числами и многочленами. Идём по этому пути дальше и вспоминаем, что многочлены можно складывать, группируя слагаемые и приводя подобные:
Точно так же можно определить и сложение (да и вычитание) двух комплексных чисел. Всё просто:
Другими словами, при сложении комплексных чисел отдельно складываются их действительные части и отдельно — мнимые. То же самое для вычитания.
Не нужно учить эти формулы. Дальше будут формулы умножения и деления — они ещё сложнее. Нужно понять ключевую идею: мы работаем с комплексными числами точно так же, как с многочленами. С небольшим дополнением: все степени комплексной единицы выше первой «сжигаются» прямо по определению самой единицы:
Небольшое замечание. В отличие от математики 5—6 классов, в серьёзной «взрослой» алгебре нет такого понятия как «вычитание». Зато есть понятие противоположного элемента и алгебраической суммы:
Всё это в полной мере относится и к комплексным числам. Там тоже есть противоположные:
Есть ноль (нейтральный элемент по сложению):
\[\begin
В общем, множество комплексных чисел — это абсолютно «нормальное» множество с понятной операцией сложения. Буквально через пару минут мы определим и умножение, но сначала давайте всё-таки запишем определение самого множества комплексных чисел.
Записывается это так:
Не пугайтесь, когда увидите подобную запись где-нибудь в учебнике алгебры. По сути, это краткая запись всего того, о чём мы говорили выше. Ничего нового мы здесь не узнали.
А вот что действительно представляет интерес — сейчас узнаем.:)
4. Геометрическая интерпретация комплексных чисел
Такие упорядоченные пары удобно рассматривать как координаты точек. По горизонтали (ось абсцисс) мы будем отмечать действительную часть числа, а по вертикали (ось ординат) — мнимую.
Определение. Комплексная плоскость — декартова система координат, где по горизонтали отмечается действительная часть комплексного числа, а по вертикали — мнимая.
Рассмотрим несколько примеров. Отметим на комплексной плоскости числа:
4.1. Ещё раз о сложении и вычитании
Такое представление чисел — в виде точек на комплексной плоскости — называется геометрической интерпретацией. Числа в таком виде удобно складывать и вычитать. По сути, всё сводится к сложению обычных векторов.
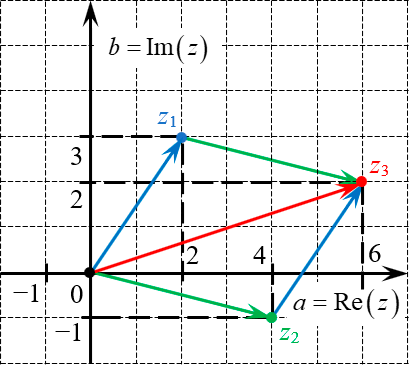
Допустим, мы хотим сложить два числа:
Отметим эти числа на комплексной плоскости, построим векторы из начала координат с концами в отмеченных точках, а затем просто сложим эти векторы (по правилу треугольника или параллелограмма — как пожелаете):
Координаты новой точки: (6; 2). Следовательно, сумма равна:
Аналогичный результат можно получить и алгебраически:
Как видим, алгебраические выкладки заняли гораздо меньше времени и места. Уже хотя бы потому что не потребовалось чертить систему координат.:)
Зачем же тогда нужна комплексная плоскость и геометрическая интерпретация? Всё встанет на свои места буквально через пару уроков, когда мы рассмотрим тригонометрическую форму записи комплексных чисел, а также будем извлекать из этих чисел корни.
А чтобы подготовиться к этим урокам, рассмотрим ещё два ключевых определения.
5. Комплексно-сопряжённые и модуль числа
Для начала вспомним школьную алгебру. Работа с многочленами, 7-й класс:
называется разностью квадратов и является одной из формул сокращённого умножения.
В математических классах с помощью сопряжённых искали обратные числа, чтобы затем решать сложные показательные и логарифмические уравнения:
Теперь настало время комплексных чисел. В них тоже можно ввести понятие сопряжённых.
5.1. Комплексно-сопряжённые
Комплексно-сопряжённые числа отмечаются чертой сверху.
Рассмотрим несколько примеров:
Видим, что комплексно-сопряжённое к «чисто мнимому» числу есть число, ему противоположное. А комплексно-сопряжённое к действительному числу есть само это число.
Зачем нужны комплексно-сопряжённые? Вспомним всё ту же формулу разности квадратов:
Итак, произведение числа на комплексно-сопряжённое даёт сумму квадратов действительной и мнимой части. Это ключевое свойство комплексно-сопряжённых, и оно позволяет нам рассмотреть следующее определение.
5.2. Модуль комплексного числа
Снова вспомним школьную алгебру. Модуль действительного числа определяют так:
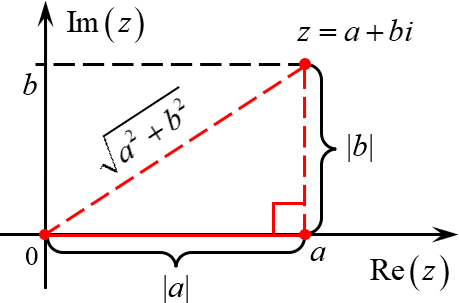
Ключевая идея: модуль числа — это всегда неотрицательная величина, равная расстоянию от точки, соответствующей этому числу, до начала отсчёта. Но всё это происходит на числовой прямой. На комплексной плоскости к делу подключается теорема Пифагора.
Вновь обратимся к геометрической интерпретации:
\[b=0\Rightarrow \left| z \right|=\sqrt<<^<2>>>\]
Получается, что на множестве комплексных чисел нельзя ввести привычные нам понятия «больше» или «меньше». Поскольку каждое число характеризуется двумя независимыми параметрами (действительной и мнимой частью), нет универсальной меры, нет отношения порядка.
Можно считать это фундаментальным законом природы. Когда мы держим в голове больше одного параметра, нет больше универсального критерия успеха:
Оценка одного и того же события будет меняться в зависимости от настроения и наших предпочтений.
Модуль числа нам пригодится в следующем уроке. А вот комплексно-сопряжённые мы будем применять уже сейчас.
6. Умножение и деление комплексных чисел
Комплексные числа можно не только складывать и вычитать, но даже умножать и делить друг на друга.
6.1. Умножение
С умножением ничего особенного.
\[\begin
Как видим, произведение комплексных чисел вновь даёт комплексное число.
Как и в случае со сложением, не нужно учить эти формулы наизусть. Лучше просто потренироваться и понять сам механизм:
Достаточно решить 10—15 таких примеров — и никакие специальные формулы и определения вам больше не понадобятся. То же самое и с делением.
6.2. Деление
Финальный бросок — попробуем разделить одно комплексное число на другое. Разумеется, делитель не должен быть нулём, иначе частное не определено.
Частное комплексных чисел вновь будет комплексным числом.
Саму формулу не нужно запоминать. Достаточно лишь отметить для себя, что мы умножили числитель и знаменатель дроби на комплексно-сопряжённое к знаменателю. Само деление можно выполнять напролом:
Тем не менее, даже после основательной тренировки умножение и особенно деление комплексных чисел остаётся трудоёмкой операцией, где можно допустить множество ошибок. Поэтому для таких операций (а также для кое-чего гораздо более серьёзного) математики придумали другую форму записи комплексных чисел — тригонометрическую. С ней мы и познакомимся на следующем уроке.:)
Комплексно сопряженные числа
Вы будете перенаправлены на Автор24
Выписать действительную и мнимую части для заданных комплексных чисел:
Комплексная плоскость
Любое комплексное число можно изобразить на плоскости, которую принято называть комплексной плоскостью. Комплексная плоскость аналогична прямоугольной декартовой системе координат, исключение составляют только названия осей:
Общий вид комплексной плоскости представлен на рис.1.
Готовые работы на аналогичную тему
Зная действительную и мнимую части комплексного числа, записать данное число:
Зная действительную и мнимую части комплексного числа, изобразить данное число на комплексной плоскости:
Записать комплексно-сопряженные числа для заданных комплексных чисел:
Отмечая соответствующие точки на плоскости, получим изображение комплексных чисел (рис.3)
Если комплексное число изображается точкой на вещественной оси, то комплексно-сопряженное число изображается той же самой точкой.
Изобразить на комплексной плоскости числа комплексно-сопряженные к отмеченным.
Изображая комплексно-сопряженные числа на комплексной плоскости, воспользуемся примечаниями 1 и 2.
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 11 11 2021
Комплексно сопряженные числа
Сопряженное (или комплексно сопряженное) число с комплексным числом \(\ z=x+i y \) является числом \(\ \overline
поиска для комплексного числа \(\ z=-34-i \) является его сопряженное число.
Следовательно, сопряженное число имеет вид: \(\ \overline
На комплексной плоскости сопряженные числа зеркалируются относительно оси действительных чисел.
Свойства комплексно-сопряженных чисел
1. \(\ |z|=|z| \), т. е. модули сопряженных чисел равны.
Модуль комплексного числа \(\ z=-4+i \) равен \(\ r=\sqrt<(-4)^<2>+1^<2>>=\sqrt <17>\). Присоединенным к комплексному числу является число \(\ z=-4-i \), модуль \(\ r=\sqrt<(-4)^<2>+(-1)^<2>>=\sqrt <17>\) которого равен модулю исходного числа.
2. \(\ \arg z=-\arg \overline
3. \(\ \overline<\overline
4. \(\ z \cdot \overline
5.\(\ z+\overline
6.\(\ \overline
7.\(\ \overline
Примеры решения проблем
Чтобы умножить комплексное число \(\ z=4-7 i \) на его сопряженное.
\(\ z \cdot \overline
Чтобы найти сопряженное к частному два комплексных числа: \(\ z 1=1-3 i \), \(\ z 2=2+5 i \).
Фактор комплексных чисел определяется путем умножения числителя и знаменателя на сопряженное число:
Мы получим тот же результат, если найдем фактор сопряженных чисел \(\ z \rceil=1-3 i \), \(\ z 2=2+5 i \):
Комплексно сопряженные числа
Комплексное число называется сопряженным к числу 
Отметим некоторые свойства комплексного сопряжения.
Доказательства этих свойств не должны вызывать сложности. Докажем, например, свойство 2:
Благодаря свойству 5, мы можем числа и называть парой комплексно сопряженных чисел.
Отметим еще одно важное свойство комплексного сопряжения.
Действительно, это важное утверждение следует из свойств комплексного сопряжения.
Пример Найти многочлен
-го порядка, у которого числа и являются корнями, а коэффициент при старшей степени равен
.
Таким образом, искомый многочлен:
Длины волн инфракрасного света достаточно велики, чтобы перемещаться сквозь облака, которые в противном случае блокировали бы наш обзор. Используя большие инфракра сные телескопы, астрономы смогли заглянуть в ядро нашей галактики. Большое количество звезд излучают часть своей электромагнитной энергии в виде видимого света, крошечной части спектра, к которой чувствительны наши глаза.
Так как длина волны коррелирует с энергией, цвет звезды говорит нам, насколько она горячая. Используя телескопы, чувствительные к различным диапазонам длин волн спектра, астрономы получают представление о широком круге объектов и явлений во вселенной.
Пример №1 Постройте центральную симметрию тетраэдра, относительно точки O, изображенных на рисунке 3.
Для построения такой центральной симметрии сначала проведем через все точки тетраэдра прямые, каждая из которых будет проходить через точку O. На них построим отрезки, удовлетворяющие условиям |AO|=|A?O|, |BO|=|B?O|, |CO|=|C?O|, |DO|=|D?O| Таким образом, и получим искомую симметрию (рис. 4).
В ряду разных механических движений особенным значением обладают колебания. Это движения и процессы, имеющие периодичность во времени.
В среде электромагнитных явлений также значительное место заняли электромагнитные колебания. В этих колебаниях заряды, токи, электрические и магнитные поля изменяются согласно периодическим законам.
Совет №1 Велосипедист, имеющий скорость 300 м/с, или идеальный газ, оказывающий давление 100 паскалей в большой тепловой машине — это странно.
Нужна помощь с курсовой или дипломной работой?
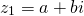
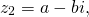
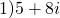
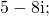
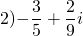
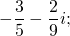


 -го порядка, у которого числа и являются корнями, а коэффициент при старшей степени равен
-го порядка, у которого числа и являются корнями, а коэффициент при старшей степени равен  .
.

