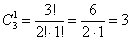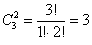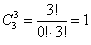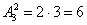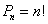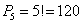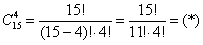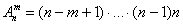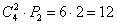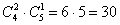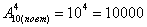Что такое комбинаторная задача

Примеры решений задач по комбинаторике

Калькуляторы онлайн и примеры

Задачи по комбинаторике с решениями онлайн

Задача 1. У мамы 2 яблока и 3 груши. Каждый день в течение 5 дней подряд она выдает по одному фрукту. Сколькими способами это может быть сделано?

Задача 3. В пассажирском поезде 9 вагонов. Сколькими способами можно рассадить в поезде 4 человека, при условии, что все они должны ехать в различных вагонах?

Задача 4. В группе 9 человек. Сколько можно образовать разных подгрупп при условии, что в подгруппу входит не менее 2 человек?

Задача 5. Группу из 20 студентов нужно разделить на 3 бригады, причем в первую бригаду должны входить 3 человека, во вторую — 5 и в третью — 12. Сколькими способами это можно сделать.

Задача 6. Для участия в команде тренер отбирает 5 мальчиков из 10. Сколькими способами он может сформировать команду, если 2 определенных мальчика должны войти в команду?

Задача 7. В шахматном турнире принимали участие 15 шахматистов, причем каждый из них сыграл только одну партию с каждым из остальных. Сколько всего партий было сыграно в этом турнире?

Задача 8. Сколько различных дробей можно составить из чисел 3, 5, 7, 11, 13, 17 так, чтобы в каждую дробь входили 2 различных числа? Сколько среди них будет правильных дробей?

Задача 9. Сколько слов можно получить, переставляя буквы в слове Гора и Институт?

Задача 10. Каких чисел от 1 до 1 000 000 больше: тех, в записи которых встречается единица, или тех, в которых она не встречается?

Готовые примеры

Нужны решенные задачи по комбинаторике? Найди в решебнике:

Источник

Комбинаторные задачи

Комбинато́рика (Комбинаторный анализ) — раздел математики, изучающий дискретные объекты, множества (сочетания, перестановки, размещения и перечисление элементов) и отношения на них (например, частичного порядка). Комбинаторика связана со многими другими областями математики — алгеброй, геометрией, теорией вероятностей, и имеет широкий спектр применения, например в информатике и статистической физике.

Термин «комбинаторика» был введён в математический обиход Лейбницем, который в 1666 году опубликовал свой труд «Рассуждения о комбинаторном искусстве».

Иногда под комбинаторикой понимают более обширный раздел дискретной математики, включающий, в частности, теорию графов.

Содержание

Примеры комбинаторных конфигураций и задач

Для формулировки и решения комбинаторных задач используют различные модели комбинаторных конфигураций. Примерами комбинаторных конфигураций являются:

Примерами комбинаторных задач являются:

Разделы комбинаторики

Перечислительная комбинаторика

Перечислительная комбинаторика (или исчисляющая комбинаторика) рассматривает задачи о перечислении или подсчёте количества различных конфигураций (например, перестановок) образуемых элементами конечных множеств, на которые могут накладываться определенные ограничения, такие как: различимость или неразличимость элементов, возможность повторения одинаковых элементов и т. п.

Количество конфигураций, образованных несколькими манипуляциями над множеством, подсчитывается согласно правилам сложения и умножения.

Типичным примером задач данного раздела является подсчете количества перестановок (см. выше). Число перестановок n-элементного множества равно факториалу числа n, то есть n!. Другой пример — известная Задача о письмах.

Структурная комбинаторика

К данному разделу относятся некоторые вопросы теории графов, а также теории матроидов.

Экстремальная комбинаторика

Примером этого раздела может служить следующая задача: какова наибольшая размерность графа, удовлетворяющего определенным свойствам.

Теория Рамсея

Теория Рамсея изучает наличие регулярных структур в случайных конфигурациях элементов. Примером утверждения из теории Рамсея может служить следующее:

в группе из 6 человек всегда можно найти три человека, которые либо попарно знакомы друг с другом, либо попарно незнакомы.

В терминах структурной комбинаторики это же утверждение формулируется так:

в любом графе с 6 вершинами найдется либо клика, либо независимое множество размера 3.

Вероятностная комбинаторика

Этот раздел отвечает на вопросы вида: какова вероятность присутствия определенного свойства у заданного множества.

Топологическая комбинаторика

Аналоги комбинаторных концепций и методов используются и в топологии, при изучении дерева принятия решений, частично упорядоченных множеств, раскрасок графа и др.

См. также

Литература

Полезное

Смотреть что такое «Комбинаторные задачи» в других словарях:

КОМБИНАТОРНЫЕ ЗАДАЧИ — класс и ческ незадачи выбора и расположения элементов конечного множества, имеющие в качестве исходной нек рую формулировку развлекательного содержания типа головоломок. Одной из классических К. з., фигурирующей еще в мифах Древнего Востока,… … Математическая энциклопедия

Комбинаторные методы решения экономических задач — [com­binatorial methods in economics] совокупность (не вполне определенная) методов, основанных на идеях комбинаторики отдела математики, изучающего вопросы, связанные с размещением и взаимным расположением частей конечного множества объектов. С… … Экономико-математический словарь

комбинаторные методы решения экономических задач — Совокупность (не вполне определенная) методов, основанных на идеях комбинаторики отдела математики, изучающего вопросы, связанные с размещением и взаимным расположением частей конечного множества объектов. С помощью этих методов решаются… … Справочник технического переводчика

КОМБИНАТОРНЫЙ АНАЛИЗ — комбинаторная математика, комбинаторика, раздел математики, посвященный решению задач выбора и расположения элементов нек рого, обычно конечного, множества в соответствии с заданными правилами. Каждое такое правило определяет способ построения… … Математическая энциклопедия

История комбинаторики — освещает развитие комбинаторики раздела конечной математики, который исследует в основном различные способы выборки заданного числа m элементов из заданного конечного множества: размещения, сочетания, перестановки, а также перечисление и смежные… … Википедия

Удовлетворение ограничений — Содержание 1 Введение 2 История 3 Примеры задач удовлетворения ограничений … Википедия

ВЕРОЯТНОСТЕЙ ТЕОРИЯ — занимается изучением событий, наступление которых достоверно неизвестно. Она позволяет судить о разумности ожидания наступления одних событий по сравнению с другими, хотя приписывание численных значений вероятностям событий часто бывает излишним… … Энциклопедия Кольера

Нейронная сеть Хопфилда — Нейронная сеть Хопфилда полносвязная нейронная сеть с симметричной матрицей связей. В процессе работы динамика таких сетей сходится (конвергирует) к одному из положений равновесия. Эти положения равновесия являются локальными минимумами… … Википедия

ВЕРОЯТНОСТЕЙ ТЕОРИЯ — математическая наука, позволяющая по вероятностям одних случайных событий находить вероятности других случайных событий, связанных к. л. образом с первыми. Утверждение о том, что к. л. событие наступает с вероятностью, равной, напр., 1/2, еще не… … Математическая энциклопедия

Псевдополиномиальный алгоритм — полиномиальный алгоритм, проявляющий экспоненциальный характер только при очень больших значениях числовых параметров. Более строгое определение выглядит так. Пусть M(z) – некоторая функция, задающая значение числового параметра индивидуальной… … Википедия

Источник

«Комбинаторные задачи и способы их решения»

Онлайн-конференция

«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»

Свидетельство и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

Комбинаторные задачи и способы их решения Выполнил учащийся 6 класса средней школы при Посольстве России в Израиле Мидхатов Казим учитель математики Акишина Л.В.

Оглавление. Введение. Что такое комбинаторика и комбинаторные задачи. Из истории комбинаторики. Способы решения комбинаторных задач. Комбинаторные задачи. Используемая литература.

1. Введение. Представителям самых различных специальностей приходится решать задачи, в которых рассматриваются те или иные комбинации, составленные из букв, цифр и иных объектов. Начальнику цеха надо распределить несколько видов работ между имеющимися станками, агроному – разместить посевы сельскохозяйственных культур на нескольких полях, заместителю директора школы – составить расписание уроков, ученому- химику – рассмотреть возможные связи между атомами и молекулами, лингвисту- учесть различные варианты значений букв незнакомого языка и т.д. Очень часто и нам в жизни приходится делать выбор, принимать решение. Это сделать очень трудно, потому что приходится выбирать из множества возможных вариантов, различных способов, комбинаций. И нам всегда хочется, чтобы этот выбор был правильным. В этом нам помогают комбинаторные задачи, решая которые мы учимся думать необычно, оригинально, смело.

2. Что такое комбинаторика и комбинаторные задачи. Область математики, в которой изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов, называется комбинаторикой. Слово «комбинаторика» происходит от латинского слова combinate, которое означает «соединять», «сочетать». Комбинаторные задачи – это задачи, требующие осуществления перебора всех возможных вариантов или подсчета их числа.

Древний период. Комбинаторные мотивы можно заметить в символике китайской «Книги Перемен» (V век до н. э.). По мнению её авторов, всё в мире комбинируется из различных сочетаний мужского и женского начал, а также восьми стихий: земля, горы, вода, ветер, гроза, огонь, облака и небо. Историки отмечают также комбинаторные проблемы в руководствах по игре в Го и другие игры. Большой интерес математиков многих стран с древних времён неизменно вызывали магические квадраты. Классическая задача комбинаторики: «сколько есть способов извлечь m элементов из N возможных» упоминается ещё в сутрах древней Индии (начиная примерно с IV века до н. э.). Индийские математики, видимо, первыми открыли биномиальные коэффициенты и их связь с биномом Ньютона. Во II веке до н. э. индийцы знали, что сумма всех биноминальных коэффициен- тов степени n равна. Античные греки также рассматривали отдельные комбинаторные задачи, хотя систематическое изложение ими этих вопросов, если оно и существовало, до нас не дошло. Хрисипп (III век до н. э.) и Гиппарх (II век до н. э.) подсчитывали, сколько следствий можно получить из 10 аксиом; методика подсчёта нам неизвестна, но у Хрисиппа получилось более миллиона, а у Гиппарха — более 100000. Аристотель при изложении своей логики безошибочно перечислил все возможные типы трёхчленных силлогизмов. Аристоксен рассмотрел различные чередования длинных и коротких слогов в стихотворных размерах. Какие-то комбинаторные правила пифагорейцы, вероятно, использовали при построении своей теории чисел и нумерологии (совершенные числа, фигурные числа, пифагоровы тройки и др.).

Средневековье. В XII веке индийский математик Бхаскара в своём основном труде «Лилавати» подробно исследовал задачи, связанные с перестановками и сочетаниями, включая перестановки с повторениями. В Западной Европе ряд глубоких открытий в области комбинаторики сделали два еврейских исследователя, Авраам ибн Эзра (XII век) и Леви бен Гершом (он же Герсонид, XIV век). Ибн Эзра обнаружил симметричность биномиальных коэффициентов, а Герсонид дал явные формулы для их подсчёта и применения в задачах вычисления числа размещений и сочетаний. Несколько комбинаторных задач содержит «Книга абака» (Фибоначчи, XIII век). Например, он поставил задачу найти наименьшее число гирь, достаточное для взвешивания любого товара весом от 1 до 40 фунтов.

Новое время Как наука комбинаторика возникла в XVI веке. В жизни привилегированных слоев тогдашнего общества большое место занимали азартные игры. В карты и кости выигрывались и проигрывались золото и бриллианты, дворцы и имения, породистые кони и дорогие украшения. Широко были распространены всевозможные лотереи. Понятно, что первоначально комбинаторные задачи касались в основном азартных игр – вопросов, сколькими способами можно выбросить данное число очков, бросая две или три кости, или сколькими способами можно получить двух королей в данной карточной игре. Эти и другие проблемы азартных игр явились движущей силой в развитии комбинаторики и развивающейся одновременно с ней теории вероятностей.

Одним из первых занялся подсчетом числа различных комбинаций при игре в кости итальянский математик Тарталья. Он составил таблицу, показывающую, сколькими способами могут выпасть r костей. Однако при этом не учитывалось, что одна и та же сумма очков может быть получена различными способами (например, 1+3+4 = 4+2 +2). Теоретическое исследование вопросов комбинаторики предприняли в XVII веке французские ученые Паскаль и Ферма. Исходным пунктом их исследований тоже были проблемы азартных игр. Дальнейшее развитие комбинаторики связано с именами Якова Бернулли, Лейбница и Эйлера. Однако и у них основную роль играли приложения к различным играм (лото, солитер и др.).

4. Способы решения комбинаторных задач. Перебор различных вариантов. Дерево возможных вариантов. Составление таблиц. Правило умножения.

Дерево возможных вариантов. Самые разные комбинаторные задачи решаются с помощью составления специальных схем. Внешне такая схема напоминает дерево, отсюда и название метода – дерево возможных вариантов. Задача. Задача. Какие трехзначные числа можно составить из цифр 0, 3, 5? Решение. Построим дерево возможных вариантов, учитывая, что 0 не может быть первой цифрой в числе. Далее.

Задача № 7. В нашем классе 8 человек. Нам нужно выбрать старосту класса и его заместителя. Сколько возможно вариантов выбора старосты и его заместителя. Задача № 8. У Васи есть 2 пары обуви, 2-е брюк и три рубашки. Сколько у него вариантов одеться по-разному? Задача № 9. Имеется батон, черный хлеб, сыр, колбаса и джем. Сколько видов бутербродов можно приготовить? Задача № 10. На тарелке лежат 5 груш и 4 яблока. Сколькими способами можно выбрать один плод? Задача № 11. На тарелке лежат 5 яблок и 4 апельсина. Сколькими способами можно выбрать пару плодов, состоящую из яблока и апельсина? Задача № 12. Учащиеся 6 класса решили обменяться фотографиями. Сколько фотографий для этого потребуется, если в классе 8 человек?

6. Используемая литература. Вероятность и статистика. 5-9 кл.: пособие для общеобразоват. учеб. заведений / Е. А. Бунимович, В. А. Булычев. – 2-е изд. стереотип. – М.: Дрофа, 2004. Виленкин Н.Я. Комбинаторика, М., 1969 г. Виленкин Н.Я. «Индукция. Комбинаторика», М. «Просвещение», 1976 г. Ткачёва М. В. «Домашняя математика», М. Просвещение, 1993 г. Интернет-ресурсы.

Источник

Задачи по комбинаторике. Примеры решений

На данном уроке мы коснёмся элементов комбинаторики, которые потребуются для дальнейшего изучения теории вероятностей. Следует отметить, что комбинаторика является самостоятельным разделом высшей математики (а не частью тервера) и по данной дисциплине написаны увесистые учебники, содержание которых, порой, ничуть не легче абстрактной алгебры. Однако нам будет достаточно небольшой доли теоретических знаний, и в данной статье я постараюсь в доступной форме разобрать основы темы с типовыми комбинаторными задачами. А многие из вас мне помогут 😉

С множеством разобрались, теперь о комбинациях. Самыми распространёнными видами комбинаций являются перестановки объектов, их выборка из множества (сочетание) и распределение (размещение). Давайте прямо сейчас посмотрим, как это происходит:

Перестановки, сочетания и размещения без повторений

Не пугайтесь малопонятных терминов, тем более, некоторые из них действительно не очень удачны. Начнём с хвоста заголовка – что значит «без повторений»? Это значит, что в данном параграфе будут рассматриваться множества, которые состоят из различных объектов. Например, … нет, кашу с паяльником и лягушкой предлагать не буду, лучше что-нибудь повкуснее =) Представьте, что перед вами на столе материализовалось яблоко, груша и банан (при наличии таковых ситуацию можно смоделировать и реально). Выкладываем фрукты слева направо в следующем порядке:

яблоко / груша / банан

Вопрос первый: сколькими способами их можно переставить?

Одна комбинация уже записана выше и с остальными проблем не возникает:

яблоко / банан / груша
груша / яблоко / банан
груша / банан / яблоко
банан / яблоко / груша
банан / груша / яблоко

Итого: 6 комбинаций или 6 перестановок.

Хорошо, здесь не составило особого труда перечислить все возможные случаи, но как быть, если предметов больше? Уже с четырьмя различными фруктами количество комбинаций значительно возрастёт!

Пожалуйста, откройте справочный материал Основные формулы комбинаторики (методичку удобно распечатать) и в пункте № 2 найдите формулу количества перестановок.

Никаких мучений – 3 объекта можно переставить 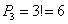способами.

Вопрос второй: сколькими способами можно выбрать а) один фрукт, б) два фрукта, в) три фрукта, г) хотя бы один фрукт?

Зачем выбирать? Так нагуляли же аппетит в предыдущем пункте – для того, чтобы съесть! =)

а) Один фрукт можно выбрать, очевидно, тремя способами – взять либо яблоко, либо грушу, либо банан. Формальный подсчёт проводится по формуле количества сочетаний:

Запись 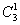в данном случае следует понимать так: «сколькими способами можно выбрать 1 фрукт из трёх?»

б) Перечислим все возможные сочетания двух фруктов:

яблоко и груша;
яблоко и банан;
груша и банан.

Количество комбинаций легко проверить по той же формуле:

Запись 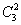понимается аналогично: «сколькими способами можно выбрать 2 фрукта из трёх?».

в) И, наконец, три фрукта можно выбрать единственным способом:

Кстати, формула количества сочетаний сохраняет смысл и для пустой выборки:
способом можно выбрать ни одного фрукта – собственно, ничего не взять и всё.

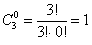
г) Сколькими способами можно взять хотя бы один фрукт? Условие «хотя бы один» подразумевает, что нас устраивает 1 фрукт (любой) или 2 любых фрукта или все 3 фрукта:
способами можно выбрать хотя бы один фрукт.

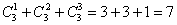
Читатели, внимательно изучившие вводный урок по теории вероятностей, уже кое о чём догадались. Но о смысле знака «плюс» позже.

Для ответа на следующий вопрос мне требуется два добровольца… …Ну что же, раз никто не хочет, тогда буду вызывать к доске =)

Вопрос третий: сколькими способами можно раздать по одному фрукту Даше и Наташе?

Для того чтобы раздать два фрукта, сначала нужно их выбрать. Согласно пункту «бэ» предыдущего вопроса, сделать это можно 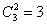способами, перепишу их заново:

яблоко и груша;
яблоко и банан;
груша и банан.

Но комбинаций сейчас будет в два раза больше. Рассмотрим, например, первую пару фруктов:
яблоком можно угостить Дашу, а грушей – Наташу;
либо наоборот – груша достанется Даше, а яблоко – Наташе.

И такая перестановка возможна для каждой пары фруктов.

В данном случае работает формула количества размещений:

Она отличается от формулы 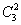тем, что учитывает не только количество способов, которым можно выбрать несколько объектов, но и все перестановки объектов в каждой возможной выборке. Так, в рассмотренном примере, важно не только то, что можно просто выбрать, например, грушу и банан, но и то, как они будут распределены (размещены) между Дашей и Наташей.

Пожалуйста, внимательно прочитайте пункт № 2 методички Основные формулы комбинаторики и постарайтесь хорошо уяснить разницу между перестановками, сочетаниями и размещениями. В простейших случаях можно пересчитать все возможные комбинации вручную, но чаще всего это становится неподъемной задачей, именно поэтому и нужно понимать смысл формул.

Также напоминаю, что сейчас речь идёт о множестве с различными объектами, и если яблоко/грушу/банан заменить на 3 яблока или даже на 3 очень похожих яблока, то в контексте рассмотренной задачи они всё равно будут считаться различными.

Остановимся на каждом виде комбинаций подробнее:

Перестановки

Перестановками называют комбинации, состоящие из одних и тех же 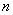различных объектов и отличающиеся только порядком их расположения. Количество всех возможных перестановок выражается формулой

Отличительной особенностью перестановок является то, что в каждой из них участвует ВСЁ множество, то есть, все 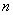объектов. Например, дружная семья:

Сколькими способами можно рассадить 5 человек за столом?

Решение: используем формулу количества перестановок:

Ответ: 120 способами

Невероятно, но факт. Обратите внимание, что здесь не имеет значения круглый ли стол, квадратный, или вообще все люди сели встали, легли на скамейку вдоль одной стены – важно лишь количество объектов и их взаимное расположение. Помимо перестановок людей, часто встречается задача о перестановках различных книг на полке, но это было бы слишком просто даже для чайника:

Сколько четырёхзначных чисел можно составить из четырёх карточек с цифрами 0, 5, 7, 9?

Для того чтобы составить четырёхзначное число нужно задействовать все четыре карточки (цифры на которых различны!), и это очень важная предпосылка для применения формулы 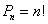Очевидно, что, переставляя карточки, мы будем получать различные четырёхзначные числа, … стоп, а всё ли тут в порядке? 😉

Хорошенько подумайте над задачей! Вообще, это характерная черта комбинаторных и вероятностных задач – в них НУЖНО ДУМАТЬ. И зачастую думать по-житейски, как, например, в разборе вступительного примера с фруктами. Нет, конечно, я не призываю тупо прорабатывать другие разделы математики, однако должен заметить, что те же интегралы можно научиться решать чисто механически.

Решение и ответ в конце урока.

Сочетания

В учебниках обычно даётся лаконичное и не очень понятное определение сочетаний, поэтому, в моих устах формулировка будет не особо рациональной, но, надеюсь, доходчивой:

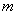
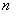
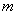
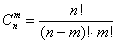
Сочетаниями называют различные комбинации из объектов, которые выбраны из множества различных объектов, и которые отличаются друг от друга хотя бы одним объектом. Иными словами, отдельно взятое сочетание – это уникальная выборка из элементов, в которой не важен их порядок (расположение). Общее же количество таких уникальных сочетаний рассчитывается по формуле .

В ящике находится 15 деталей. Сколькими способами можно взять 4 детали?

Решение: прежде всего, снова обращаю внимание на то, что по логике условия, детали считаются различными – даже если они на самом деле однотипны и визуально одинаковы
(в этом случае их можно, например, пронумеровать).

В задаче речь идёт о выборке из 4 деталей, в которой не имеет значения их «дальнейшая судьба» – грубо говоря, «просто выбрали 4 штуки и всё». Таким образом, у нас имеют место сочетания деталей. Считаем их количество:

Здесь, конечно же, не нужно ворочать огромные числа .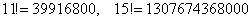
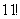
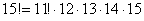
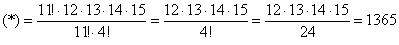
В похожей ситуации я советую использовать следующий приём: в знаменателе выбираем наибольший факториал (в данном случае ) и сокращаем на него дробь. Для этого числитель следует представить в виде . Распишу очень подробно:

способами можно взять 4 детали из ящика.

Ещё раз: что это значит? Это значит, что из набора 15 различных деталей можно составить одну тысячу триста шестьдесят пять уникальных сочетания 4 деталей. То есть, каждая такая комбинация из четырёх деталей будет отличаться от других комбинаций хотя бы одной деталью.

Ответ: 1365 способами

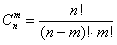
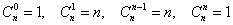
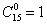
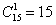
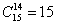
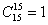
Формуле необходимо уделить самое пристальное внимание, поскольку она является «хитом» комбинаторики. При этом полезно ПОНИМАТЬ и без всяких вычислений записывать «крайние» значения: . Применительно к разобранной задаче:

– единственным способом можно не выбрать ни одной детали;
способами можно взять 1 деталь (любую из пятнадцати);
способами можно взять 14 деталей (при этом какая-то одна из 15 останется в ящике);
– единственным способом можно взять все пятнадцать деталей.

Рекомендую внимательно ознакомиться с биномом Ньютона и треугольником Паскаля, по которому, к слову, очень удобно выполнять проверку вычислений 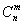при небольших значениях «эн».

Сколькими способами из колоды в 36 карт можно выбрать 3 карты?

Это пример для самостоятельного решения. Чем приятны многие комбинаторные задачи, так это краткостью – главное, разобраться в сути. И суть, бывает, открывается с различных сторон. Разберём весьма поучительный пример:

В шахматном турнире участвует 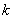человек и каждый с каждым играет по одной партии. Сколько всего партий сыграно в турнире?

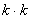
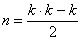
Поскольку я сам играю в шахматы и неоднократно принимал участие в круговых турнирах, то сразу же сориентировался по турнирной таблице размером клеток, в которой результат каждой партии учитывается дважды и, кроме того, затушёвываются клетки «главной диагонали» (т.к. участники не играют сами с собой). Исходя из проведённых рассуждений, общее количество сыгранных партий рассчитывается по формуле . Такое решение полностью корректно (см. соответствующий файл банка готовых решений) и на долгое время я забыл о нём по принципу «решено, да и ладно».

Однако один из посетителей сайта заметил, что на самом деле здесь можно руководствоваться самыми что ни на есть банальными сочетаниями:
различных пар можно составить из соперников (кто играет белыми, кто чёрными – не важно).

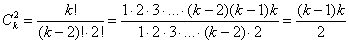
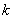
Эквивалентной является задача о рукопожатиях: в отделе работает 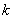мужчин и каждый с каждым здоровается за руку, сколько рукопожатий они совершают? К слову, шахматисты тоже пожимают друг другу руку перед каждой партией.

Ну а вывода тут два:
– во-первых, не всё очевидное – очевидно;
– и во-вторых, не бойтесь решать задачи «нестандартно»!

Большое спасибо за ваши письма, они помогают улучшить качество учебных материалов!

Размещения

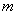
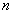
Или «продвинутые» сочетания. Размещениями называют различные комбинации из объектов, которые выбраны из множества различных объектов, и которые отличаются друг от друга как составом объектов в выборке, так и их порядком. Количество размещений рассчитывается по формуле

Что наша жизнь? Игра:

Боря, Дима и Володя сели играть в «очко». Сколькими способами им можно сдать по одной карте? (колода содержит 36 карт)

Решение: ситуация похожа на Задачу 4, но отличается тем, что здесь важно не только то, какие три карты будут извлечены из колоды, но и то, КАК они будут распределены между игроками. По формуле размещений:

способами можно раздать 3 карты игрокам.

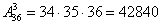
Есть и другая схема решения, которая, с моей точки зрения, даже понятнее:

способами можно извлечь 3 карты из колоды.

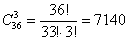
КП, 9Ч, 7Ч;
КП, 7Ч, 9Ч;
9Ч, КП, 7Ч;
9Ч, 7Ч, КП;
7Ч, КП, 9Ч;
7Ч, 9Ч, КП.

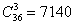
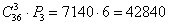
И аналогичный факт справедлив для любого уникального набора из трёх карт. А таких наборов, не забываем, мы насчитали . Не нужно быть профессором, чтобы понять, что найденное количество сочетаний следует умножить на шесть:

способами можно сдать по одной карте трём игрокам.

По существу, получилась наглядная проверка формулы 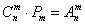, окончательный смысл которой мы проясним в следующем параграфе.

Ответ: 42840

Возможно, у вас остался вопрос, а кто же раздавал карты? …Наверное, преподаватель =)
И чтобы никому не было обидно, в следующей задаче примет участие вся студенческая группа:

В студенческой группе 23 человека. Сколькими способами можно выбрать старосту и его заместителя?

Задача о «размещении» должностей в коллективе встречается очень часто и является самым настоящим баяном. Краткое решение и ответ в конце урока.

Правило сложения и правило умножения комбинаций

Данные правила весьма напоминают алгебру событий, и многие читатели уже ознакомились с пунктом № 4 справочного материала Основные формулы комбинаторики, где они изложены в общем виде. Постараюсь повторить принципы максимально кратко:

1) Знак «плюс» следует понимать и читать как союз ИЛИ. Вспоминаем демонстрационную задачу с яблоком, грушей и бананом:

способами можно выбрать хотя бы один фрукт.

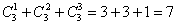
То есть, можно взять 1 фрукт (любой из трёх) ИЛИ какое-нибудь сочетание двух фруктов ИЛИ все три фрукта. Заметьте, что сложение комбинаций предполагает безразличие выбора (без разницы будет ли выбран один, два или 3 фрукта).

Рассмотрим более основательный пример:

Студенческая группа состоит из 23 человек, среди которых 10 юношей и 13 девушек. Сколькими способами можно выбрать двух человек одного пола?

Решение: в данном случае подсчёт 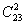не годится, поскольку общее количество сочетаний включает в себя и разнополые пары.

Условие «выбрать двух человек одного пола» подразумевает, что необходимо выбрать двух юношей или двух девушек, и уже сама словесная формулировка указывает на верный путь решения:

способами можно выбрать 2 юношей;
способами можно выбрать 2 девушек.

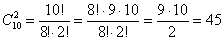
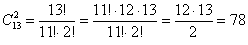
Таким образом, двух человек одного пола (без разницы – юношей или девушек) можно выбрать: 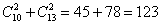способами.

Ответ: 123

Правило умножения комбинаций:

2) Знак «умножить» следует понимать и читать как союз И.

Рассмотрим ту же студенческую группу, которая пошла на танцы. Сколькими способами можно составить пару из юноши и девушки?

способами можно выбрать 1 юношу;
способами можно выбрать 1 девушку.

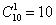
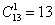
Таким образом, одного юношу и одну девушку можно выбрать: 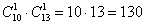способами.

Когда из каждого множества выбирается по 1 объекту, то справедлив следующий принцип подсчёта комбинаций: «каждый объект из одного множества может составить пару с каждым объектом другого множества».

То есть, Олег может пригласить на танец любую из 13 девушек, Евгений – тоже любую из тринадцати, и аналогичный выбор есть у остальных молодых людей. Итого: 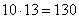возможных пар.

Следует отметить, что в данном примере не имеет значения «история» образования пары; однако если принять во внимание инициативу, то количество комбинаций нужно удвоить, поскольку каждая из 13 девушек тоже может пригласить на танец любого юношу. Всё зависит от условия той или иной задачи!

Похожий принцип справедлив и для более сложных комбинаций, например: сколькими способами можно выбрать двух юношей и двух девушек для участия в сценке КВН?

Союз И недвусмысленно намекает, что комбинации необходимо перемножить:

возможных групп артистов.

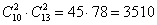
Иными словами, каждая пара юношей (45 уникальных пар) может выступать с любой парой девушек (78 уникальных пар). А если рассмотреть распределение ролей между участниками, то комбинаций будет ещё больше. …Очень хочется, но всё-таки воздержусь от продолжения, чтобы не привить вам отвращение к студенческой жизни =).

Правило умножения комбинаций распространяется и на бОльшее количество множителей:

Сколько существует трёхзначных чисел, которые делятся на 5?

Решение: для наглядности обозначим данное число тремя звёздочками: ***

Комбинации будем считать по разрядам – слева направо:

В разряд сотен можно записать любую из 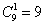цифр (1, 2, 3, 4, 5, 6, 7, 8 или 9). Ноль не годится, так как в этом случае число перестаёт быть трёхзначным.

А вот в разряд десятков («посерединке») можно выбрать любую из 10 цифр: .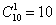

По условию, число должно делиться на 5. Число делится на 5, если оно заканчивается на 5 либо на 0. Таким образом, в младшем разряде нас устраивают 2 цифры.

Итого, существует: 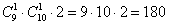трёхзначных чисел, которые делятся на 5.

При этом произведение 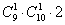расшифровывается так: «9 способами можно выбрать цифру в разряд сотен и 10 способами выбрать цифру в разряд десятков и 2 способами в разряд единиц»

Или ещё проще: «каждая из 9 цифр в разряде сотен комбинируется с каждой из 10 цифр разряда десятков и с каждой из двух цифр в разряде единиц».

Ответ: 180

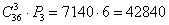
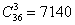
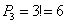
Да, чуть не забыл об обещанном комментарии к задаче № 5, в которой Боре, Диме и Володе можно сдать по одной карте способами. Умножение здесь имеет тот же смысл: способами можно извлечь 3 карты из колоды И в каждой выборке переставить их способами.

А теперь задача для самостоятельного решения… сейчас придумаю что-нибудь поинтереснее, …пусть будет про ту же русскую версию блэкджека:

Сколько существует выигрышных комбинаций из 2 карт при игре в «очко»?

Для тех, кто не знает: выигрывает комбинация 10 + ТУЗ (11 очков) = 21 очко и, давайте будем считать выигрышной комбинацию из двух тузов.

(порядок карт в любой паре не имеет значения)

Краткое решение и ответ в конце урока.

Кстати, не надо считать пример примитивным. Блэкджек – это чуть ли не единственная игра, для которой существует математически обоснованный алгоритм, позволяющий выигрывать у казино. Желающие могут легко найти массу информации об оптимальной стратегии и тактике. Правда, такие мастера довольно быстро попадают в чёрный список всех заведений =)

Пришло время закрепить пройденный материал парой солидных задач:

У Васи дома живут 4 кота.

а) сколькими способами можно рассадить котов по углам комнаты?
б) сколькими способами можно отпустить гулять котов?
в) сколькими способами Вася может взять на руки двух котов (одного на левую, другого – на правую)?

Решаем: во-первых, вновь следует обратить внимание на то, что в задаче речь идёт о разных объектах (даже если коты – однояйцовые близнецы). Это очень важное условие!

а) Молчание котов. Данной экзекуции подвергаются сразу все коты
+ важно их расположение, поэтому здесь имеют место перестановки:
способами можно рассадить котов по углам комнаты.

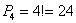
Повторюсь, что при перестановках имеет значение лишь количество различных объектов и их взаимное расположение. В зависимости от настроения Вася может рассаживать животных полукругом на диване, в ряд на подоконнике и т.д. – перестановок во всех случаях будет 24. Желающие могут для удобства представить, что коты разноцветные (например, белый, чёрный, рыжий и полосатый) и перечислить все возможные комбинации.

б) Сколькими способами можно отпустить гулять котов?

Предполагается, что коты ходят гулять только через дверь, при этом вопрос подразумевает безразличие по поводу количества животных – на прогулку могут выйти 1, 2, 3 или все 4 кота.

Считаем все возможные комбинации:

способами можно отпустить гулять одного кота (любого из четырёх);
способами можно отпустить гулять двух котов (варианты перечислите самостоятельно);
способами можно отпустить гулять трёх котов (какой-то один из четырёх сидит дома);
способом можно выпустить всех котов.

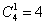
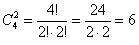
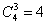
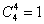
Наверное, вы догадались, что полученные значения следует просуммировать:
способами можно отпустить гулять котов.

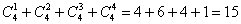
Энтузиастам предлагаю усложнённую версию задачи – когда любой кот в любой выборке может выйти на улицу, как через дверь, так и через окно 10 этажа. Комбинаций заметно прибавится! Дерзайте! А в конце урока я познакомлю вас с удивительно простым решением этого пункта.

в) Сколькими способами Вася может взять на руки двух котов?

Ситуация предполагает не только выбор 2 животных, но и их размещение по рукам:
способами можно взять на руки 2 котов.

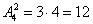
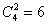
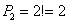
Второй вариант решения: способами можно выбрать двух котов и способами посадить каждую пару на руки:

Ответ: а) 24, б) 15, в) 12

Ну и для очистки совести что-нибудь поконкретнее на умножение комбинаций…. Пусть у Васи дополнительно живёт 5 кошек =) Сколькими способами можно отпустить гулять 2 котов и 1 кошку?

То есть, с каждой парой котов можно выпустить каждую кошку.

Ещё один баян для самостоятельного решения:

В лифт 12-этажного дома сели 3 пассажира. Каждый независимо от других с одинаковой вероятностью может выйти на любом (начиная со 2-го) этаже. Сколькими способами:

1) пассажиры могут выйти на одном и том же этаже (порядок выхода не имеет значения);
2) два человека могут выйти на одном этаже, а третий – на другом;
3) люди могут выйти на разных этажах;
4) пассажиры могут выйти из лифта?

И тут часто переспрашивают, уточняю: если 2 или 3 человека выходят на одном этаже, то очерёдность выхода не имеет значения. ДУМАЙТЕ, используйте формулы и правила сложения/умножения комбинаций. В случае затруднений пассажирам полезно дать имена и порассуждать, в каких комбинациях они могут выйти из лифта. Не нужно огорчаться, если что-то не получится, так, например, пункт № 2 достаточно коварен, впрочем, один из читателей отыскал простое решение, и я в очередной раз выражаю благодарность за ваши письма!

Полное решение с подробными комментариями в конце урока.

Заключительный параграф посвящён комбинациям, которые тоже встречаются достаточно часто – по моей субъективной оценке, примерно в 20-30% комбинаторных задач:

Перестановки, сочетания и размещения с повторениями

Перечисленные виды комбинаций законспектированы в пункте № 5 справочного материала Основные формулы комбинаторики, однако некоторые из них по первому прочтению могут быть не очень понятными. В этом случае сначала целесообразно ознакомиться с практическими примерами, и только потом осмысливать общую формулировку. Поехали:

Перестановки с повторениями

В перестановках с повторениями, как и в «обычных» перестановках, участвует сразу всё множество объектов, но есть одно но: в данном множестве один или бОльшее количество элементов (объектов) повторяются. Встречайте очередной стандарт:

Сколько различных буквосочетаний можно получить перестановкой карточек со следующими буквами: К, О, Л, О, К, О, Л, Ь, Ч, И, К?

Решение: в том случае, если бы все буквы были различны, то следовало бы применить тривиальную формулу 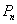, однако совершенно понятно, что для предложенного набора карточек некоторые манипуляции будут срабатывать «вхолостую», так, например, если поменять местами любые две карточки с буквами «К» в любом слове, то получится то же самое слово. Причём, физически карточки могут сильно отличаться: одна быть круглой с напечатанной буквой «К», другая – квадратной с нарисованной буквой «К». Но по смыслу задачи даже такие карточки считаются одинаковыми, поскольку в условии спрашивается о буквосочетаниях.

Всё предельно просто – всего: 11 карточек, среди которых буква:

К – повторяется 3 раза;
О – повторяется 3 раза;
Л – повторяется 2 раза;
Ь – повторяется 1 раз;
Ч – повторяется 1 раз;
И – повторяется 1 раз.

Проверка: 3 + 3 + 2 + 1 + 1 + 1 = 11, что и требовалось проверить.

По формуле количества перестановок с повторениями:
различных буквосочетаний можно получить. Больше полумиллиона!

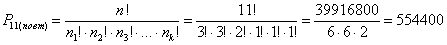
Для быстрого расчёта большого факториального значения удобно использовать стандартную функцию Экселя: забиваем в любую ячейку =ФАКТР(11) и жмём Enter.

На практике вполне допустимо не записывать общую формулу и, кроме того, опускать единичные факториалы: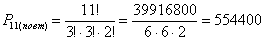

Но предварительные комментарии о повторяющихся буквах обязательны!

Ответ: 554400

Другой типовой пример перестановок с повторениями встречается в задаче о расстановке шахматных фигур, которую можно найти на складе готовых решений в соответствующей pdf-ке. А для самостоятельного решения я придумал менее шаблонное задание:

Алексей занимается спортом, причём 4 дня в неделю – лёгкой атлетикой, 2 дня – силовыми упражнениями и 1 день отдыхает. Сколькими способами он может составить себе расписание занятий на неделю?

Формула 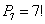здесь не годится, поскольку учитывает совпадающие перестановки (например, когда меняются местами силовые упражнения в среду с силовыми упражнениями в четверг). И опять – по факту те же 2 силовые тренировки могут сильно отличаться друг от друга, но по контексту задачи (с точки зрения расписания) они считаются одинаковыми элементами.

Двухстрочное решение и ответ в конце урока.

Сочетания с повторениями

Характерная особенность этого вида комбинаций состоит в том, что выборка проводится из нескольких групп, каждая из которых состоит из одинаковых объектов.

Сегодня все хорошо потрудились, поэтому настало время подкрепиться:

В студенческой столовой продают сосиски в тесте, ватрушки и пончики. Сколькими способами можно приобрести пять пирожков?

Решение: сразу обратите внимание на типичный критерий сочетаний с повторениями – по условию на выбор предложено не множество объектов как таковое, а различные виды объектов; при этом предполагается, что в продаже есть не менее пяти хот-догов, 5 ватрушек и 5 пончиков. Пирожки в каждой группе, разумеется, отличаются – ибо абсолютно идентичные пончики можно смоделировать разве что на компьютере =) Однако физические характеристики пирожков по смыслу задачи не существенны, и хот-доги / ватрушки / пончики в своих группах считаются одинаковыми.

Что может быть в выборке? Прежде всего, следует отметить, что в выборке обязательно будут одинаковые пирожки (т.к. выбираем 5 штук, а на выбор предложено 3 вида). Варианты тут на любой вкус: 5 хот-догов, 5 ватрушек, 5 пончиков, 3 хот-дога + 2 ватрушки, 1 хот-дог + 2 + ватрушки + 2 пончика и т.д.

Как и при «обычных» сочетаниях, порядок выбора и размещение пирожков в выборке не имеет значения – просто выбрали 5 штук и всё.

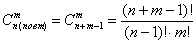
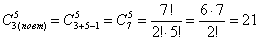
Используем формулу количества сочетаний с повторениями:
способом можно приобрести 5 пирожков.

Ответ: 21

Какой вывод можно сделать из многих комбинаторных задач?

Порой, самое трудное – это разобраться в условии.

Аналогичный пример для самостоятельного решения:

В кошельке находится достаточно большое количество 1-, 2-, 5- и 10-рублёвых монет. Сколькими способами можно извлечь три монеты из кошелька?

В целях самоконтроля ответьте на пару простых вопросов:

1) Могут ли в выборке все монеты быть разными?
2) Назовите самую «дешевую» и самую «дорогую» комбинацию монет.

Решение и ответы в конце урока.

Из моего личного опыта, могу сказать, что сочетания с повторениями – наиболее редкий гость на практике, чего не скажешь о следующем виде комбинаций:

Размещения с повторениями

Есть две основные модели, где фигурируют размещения с повторениями, рассмотрим их по порядку. Номер один:

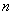
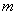
Из множества, состоящего из элементов, выбирается элементов, при этом важен порядок элементов в каждой выборке. И всё бы было ничего, но довольно неожиданный прикол заключается в том, что любой объект исходного множества мы можем выбирать сколько угодно раз. Образно говоря, от «множества не убудет».

Когда так бывает? Типовым примером является кодовый замок с несколькими дисками, но по причине развития технологий актуальнее рассмотреть его цифрового потомка:

Сколько существует четырёхзначных пин-кодов?

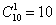
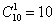
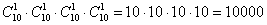
Решение: на самом деле для разруливания задачи достаточно знаний правил комбинаторики: способами можно выбрать первую цифру пин-кода и способами – вторую цифру пин-кода и столькими же способами – третью и столькими же – четвёртую. Таким образом, по правилу умножения комбинаций, четырёхзначный пин-код можно составить: способами.

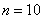
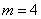
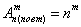
А теперь с помощью формулы. По условию нам предложен набор из цифр, из которого выбираются цифры и располагаются в определенном порядке, при этом цифры в выборке могут повторяться (т.е. любой цифрой исходного набора можно пользоваться произвольное количество раз). По формуле количества размещений с повторениями:

Ответ: 10000

Что тут приходит на ум… …если банкомат «съедает» карточку после третьей неудачной попытки ввода пин-кода, то шансы подобрать его наугад весьма призрачны.

И кто сказал, что в комбинаторике нет никакого практического смысла? Познавательная задача для всех читателей mathprofi.ru:

Согласно государственному стандарту, автомобильный номерной знак состоит из 3 цифр и 3 букв. При этом недопустим номер с тремя нулями, а буквы выбираются из набора А, В, Е, К, М, Н, О, Р, С, Т, У, Х (используются только те буквы кириллицы, написание которых совпадает с латинскими буквами).

Сколько различных номерных знаков можно составить для региона?

Не так их, кстати, и много. В крупных регионах такого количества не хватает, и поэтому для них существуют по несколько кодов к надписи RUS.

Решение и ответ в конце урока. Не забываем использовать правила комбинаторики 😉 …Хотел похвастаться эксклюзивом, да оказалось не эксклюзивом =) Заглянул в Википедию – там есть расчёты, правда, без комментариев. Хотя в учебных целях, наверное, мало кто прорешивал.

И здесь в своё время я завершил урок, но любознательные читатели всё не хотят меня отпускать! Да меня и самого не отпускает 🙂 Поэтому разберём ещё один тип задач на размещения с повторениями, они встречаются не так часто, их решение на так очевидно, но знание этого подхода здОрово облегчит жизнь. Вторая интерпретация размещений с повторениями:

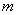
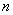
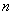
Рассмотрим объектов (или субъектов), каждый из которых может находиться в одном из состояний (или выбрать одно из возможных действий). Тогда общее число возможных состояний всего множества объектов (субъектов) рассчитывается по формуле .

У Васи дома живут 4 кота. После завтрака любой кот может уйти гулять или остаться дома.

а) Сколькими способам могут уйти гулять коты?
б) …если каждый из них может выйти на улицу, как через дверь, так и через окно?

Решение: в Задаче 10 мы прямо перечислили все возможные варианты пункта «а», но этот способ хорош лишь в простых случаях. Уже в пункте «бэ» прямой подсчёт комбинаций вызывает значительные затруднения. Но здесь есть простое и короткое решение:

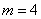
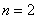
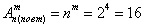
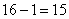
а) По условию, дано кота, при этом каждый из них может поступить способами (остаться дома / уйти гулять), таким образом, коты могут поступить:
способами, из которых следует исключить один случай (когда все коты остались дома): .

! Обязательно обращайте внимание на условие! Если там задан вопрос «Сколькими способами могут поступить коты?», то корректный ответ 16.

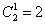
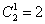
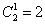
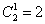
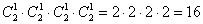
Следует отметить, что данную задачу можно решить и через перемножение комбинаций: способами может поступить 1-й кот и способами может поступить 2-й кот и способами может поступить 3-й кот и способами может поступить 4-й кот. Таким образом, коты могут поступить способами. Вот такой вот пин-кот 🙂

б) Решение проще простого. Здесь у каждого кота три опции :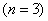
остаться дома / уйти гулять через дверь / уйти гулять через окно.

Таким образом, коты могут уйти гулять 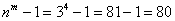способами.

Этот пункт, разумеется, тоже можно решить через умножение комбинаций.

Ответ: а) 15, б) 80

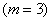
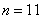
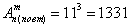
Теперь посмотрим с нового ракурса на Задачу 11, а именно ответим на вопрос «Сколькими способами могут выйти три человека из лифта?». Здесь у нас три человека , каждый из которых может выйти на любом из одиннадцати этажей ( опций). Таким образом, люди могут выйти из лифта способом.

Разумеется, в условии может идти речь и о неодушевленных объектах, такой пример встретился в первой же дополнительной задаче по комбинаторике:

«В комнате имеется 6 лампочек, каждая со своим выключателем. Сколькими способами можно освещать комнату?»

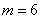
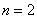
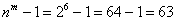
Там я опять перечислил все возможные комбинации, но есть путь короче. По сути, те же коты: в условии нам дано объектов, каждый из которых может находиться в состояниях (включено / выключено), таким образом, комнату можно осветить:
способами (вычли случай, когда все лампочки выключены).

И, конечно, я не забыл о прогульщиках – никто не отвертится от активного участия в моих уроках 🙂 Для вас заключительная задача:

В коридоре стоит шеренга из 7 студентов. По команде каждый из них должен произвольно поднять одну руку или одну ногу.

а) Сколькими способами они могут это сделать?
б) … если разрешается поднять любое количество рук / ног? (одновременное поднятие двух рук и двух ног (прыжок) тоже считается комбинацией).

Краткое решение и ответ совсем близко. Пункт «бэ», к слову, не так-то прост, я бы даже присвоил ему категорию повышенной сложности.

Что ещё важно в рассмотренных задачах? Объекты или субъекты не обязаны быть однородными. Пусть вместо 4 котов у Васи обитают кот, пёс, конь и петух. И они тоже могут уйти гулять способами.

Кроме того, у каждого объекта / субъекта могут быть разные опции: кот может уйти гулять или нет, пёс – облаять гостя или нет, конь – подмигнуть одним глазом или двумя (да, он ;)), а петух – разбудить Васю или не разбудить. Формула та же, правда, её уже нельзя назвать «размещения с повторениями», ибо у каждого животного свои уникальные действия.

И более того, у каждого объекта или субъекта может быть разное количество опций, и тогда задача решается через перемножение комбинаций.

На этом наше увлекательное занятие подошло к концу (?!), и напоследок я хочу сказать, что вы не зря потратили время – по той причине, что формулы комбинаторики находят ещё одно насущное практическое применение: они встречаются в различных задачах по теории вероятностей, и в задачах на классическое определение вероятности – особенно часто =)

Всем спасибо за активное участие и до скорых встреч!

Задача 2: Решение: найдём количество всех возможных перестановок 4 карточек: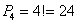

Когда карточка с нулём располагается на 1-м месте, то число становится трёхзначным, поэтому данные комбинации следует исключить. Пусть ноль находится на 1-м месте, тогда оставшиеся 3 цифры в младших разрядах можно переставить 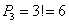способами.

Примечание: т.к. карточек немного, то здесь несложно перечислить все такие варианты:
0579
0597
0759
0795
0957
0975

Таким образом, из предложенного набора можно составить:
24 – 6 = 18 четырёхзначных чисел
Ответ: 18

З.Ы. Никогда не думал, что эти задачи будут предлагать первоклассникам, один из которых заметил, что карточку «9» можно использовать как «6», и поэтому количество комбинаций нужно удвоить. Но в условии всё же заявлена конкретная цифра и от удвоения лучше воздержаться.

Задача 4: Решение: 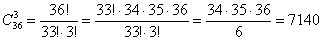способами можно выбрать 3 карты из 36.
Ответ: 7140

Задача 6: Решение: 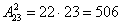способами.
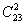
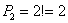
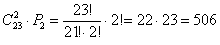
Другой вариант решения: способами можно выбрать двух человек из группы и способами распределить должности в каждой выборке. Таким образом, старосту и его заместителя можно выбрать способами.
Ответ: 506

Задача 9: Решение:
способами может быть сдана десятка и туз («каждая десятка с каждым тузом»);
способами может быть сдана пара тузов.
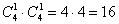
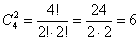
Итого: 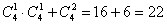выигрышные комбинации.
Ответ: 22

Задача 11: Решение:
1) способами можно выбрать этаж для выхода всех пассажиров.

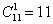
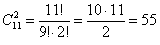
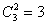
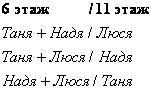
2) Способ первый: способами можно выбрать 2 этажа для выхода пассажиров (например, 6-й и 11-й этаж).
способами можно выбрать двух человек для выхода на одном этаже (третий выйдет на другом). Например:

Кроме того, любую пару и «одинокого человека» можно поменять этажами: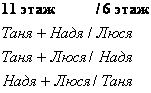

Таким образом, для каждой пары этажей (55 уникальных сочетаний) возможно 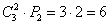способов выхода пассажиров.
По правилу умножения комбинаций: 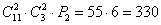способами два пассажира могут выйти на одном этаже, а третий – на другом этаже.

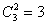
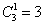
Примечание: как вариант, вместо можно использовать – способами можно выбрать одного человека (а значит, и пару).

Более компактный способ, который предложил один из читателей сайта:
способами можно выбрать пару и одного человека и для каждого случая способами выбрать два этажа для их выхода (с учётом перестановки пары и человека по этажам). Таким образом, люди могут выйти способами.

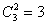
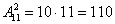
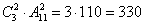
И способ третий, который нашёл ещё один читатель: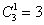
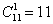
способами можно выбрать «одинокого» человека и каждый человек может выйти из лифта: способами.
И для каждой из этих комбинаций:
способами можно выбрать этаж для выхода двух других людей.
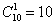
По правилу умножения комбинаций: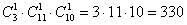
способами 1 пассажир может выйти на одном этаже, а 2 других – на другом.

3) способами пассажиры могут выйти на разных этажах.
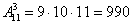
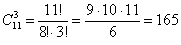
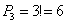
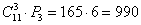
Второй вариант решения: способами можно выбрать 3 этажа для выхода и способами переставить пассажиров по каждой тройке этажей; следовательно, пассажиры могут выйти на разных этажах способами.

Третий вариант решения, нашёл другой читатель сайта. Через комбинаторное произведение: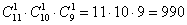

(11 способами можно выйти один пассажир и для каждого из этих вариантов – 10 способами может выйти другой пассажир и для каждой возможной комбинации их выхода – 9 способами может выйти третий пассажир)

4) Способ первый: суммируем комбинации первых трёх пунктов:
способом пассажиры могут выйти из лифта.

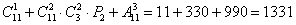
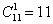
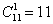
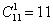
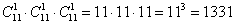
Способ второй: в общем случае он более рационален, более того, позволяет обойтись без результатов предыдущих пунктов. Рассуждения таковы: способами может выйти 1-й пассажир из лифта и способами может выйти 2-й пассажир и способами может выйти 3-й пассажир. По правилу умножения комбинаций: способом могут выйти три человека

Ответ: 1) 11; 2) 330; 3) 990; 4) 1331

Задача 13: Решение: по формуле количества перестановок с повторениями:
способами можно составить расписание занятий на неделю.
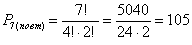
Ответ: 105

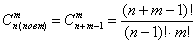
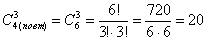
Задача 15: Решение: используем формулу сочетаний с повторениями:
способами можно выбрать 3 монеты из кошелька.
Ответ: 20
Ответы на вопросы:
1) Да (т.к. количество извлекаемых монет (3 шт.) меньше видов монет (4 вида));
2) Самый «дешёвый» набор содержит 3 рублёвые монеты, а самый «дорогой» – 3 десятирублёвые.

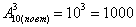
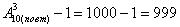
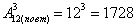
Задача 17: Решение: способами можно составить цифровую комбинацию автомобильного номера, при этом одну из них (000) следует исключить: .
способами можно составить буквенную комбинацию автомобильного номера.
По правилу умножения комбинаций, всего можно составить:
автомобильных номера
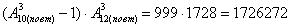
(каждая цифровая комбинация сочетается с каждой буквенной комбинацией).
Ответ: 1726272

Задача 19: Решение: используем формулу размещений с повторениями.

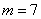
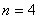
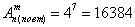
а) По условию, дано солдат, у каждого из которых есть опции (поднять левую руку / поднять правую руку / поднять левую ногу / поднять правую ногу). Таким образом, солдаты могут выполнить команду способами.

б) Дважды используем формулу размещений с повторениями.

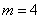
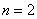
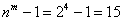
Сначала найдём все возможные комбинации поднятых конечностей: конечности, каждая из которых может находиться в состояниях (поднята или нет). Таким образом, существует комбинаций поднятых конечностей (исключили комбинацию, когда все конечности внизу)…, какой-то прямо фильм ужасов получился, а не задача в воспитательных целях 🙂

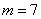
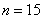
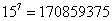
Таким образом, у каждого из солдат в распоряжении есть опций, и они могут выполнить команду способами. Невероятно, но факт.

Ответ: а) 16384, б) 170859375

Автор: Емелин Александр

(Переход на главную страницу)

Zaochnik.com – профессиональная помощь студентам

Источник