Что такое коэффициент значимости
Коэффициент значимости
9. Коэффициент значимости
Цифровое выражение степени влияния коррозионного разрушения на функциональные свойства материала или покрытия детали
Смотреть что такое «Коэффициент значимости» в других словарях:
коэффициент весомости показателя качества продукции — Количественная характеристика значимости данного показателя качества продукции среди других показателей ее качества. Пояснения Коэффициенты весомости могут определяться социологическим или экспертным методами, а также на основе анализа влияния… … Справочник технического переводчика
Коэффициент весомости показателя качества продукции — – количественная характеристика значимости данного показателя качества продукции среди других показателей ее качества. [ГОСТ 15467 79] Рубрика термина: Общие, качество Рубрики энциклопедии: Абразивное оборудование, Абразивы, Автодороги … Энциклопедия терминов, определений и пояснений строительных материалов
Коэффициент корреляции — (Correlation coefficient) Коэффициент корреляции это статистический показатель зависимости двух случайных величин Определение коэффициента корреляции, виды коэффициентов корреляции, свойства коэффициента корреляции, вычисление и применение… … Энциклопедия инвестора
Коэффициент весомости показателя качества продукции — 15. Коэффициент весомости показателя качества продукции Количественная характеристика значимости данного показателя качества продукции среди других показателей ее качества Источник: ГОСТ 15467 79: Управление качеством продукции. Основные понятия … Словарь-справочник терминов нормативно-технической документации
Коэффициент детонации — Детонация в акустике искажения звука в результате частотной модуляции посторонним сигналом с частотой 0,2 200 Гц, например, порождаемым колебаниями скорости протяжки магнитной ленты. Содержание 1 Восприятие человеком 2 Природа искажений … Википедия
Оценка значимости статистических показателей — один из основных способов статистической проверки гипотез. Статистические гипотезы чаще всего выдвигаются либо относительно вида распределения некоторого признака в генеральной совокупности (например, гипотеза о нормальном распределении… … Социологический справочник
ПРОВЕРКА ЗНАЧИМОСТИ — (significance test) (Статистика) тест, разработанный для оценки возможности случайного происхождения наблюдаемого (числового) результата, который выражен как статистический (например, коэффициент t, коэффициент F). Его можно оценить с различным… … Большой толковый социологический словарь
СТО Газпром 2-1.12-064-2006: Методика оценки технико-коммерческих предложений на поставку материально-технических ресурсов, работ и услуг — Терминология СТО Газпром 2 1.12 064 2006: Методика оценки технико коммерческих предложений на поставку материально технических ресурсов, работ и услуг: 4.2.2 Взаимосвязь обобщенных (сложных) и простых критериев. Для оценки отдельно технической,… … Словарь-справочник терминов нормативно-технической документации
Итоговая оценка — 3.4.2 Итоговая оценка технико коммерческих предложений и построение ранжированного по предпочтительности списка лотовых заявок проводится отдельно для каждого лота. Договоры на поставку товаров (выполнение работ, оказание услуг) заключаются для… … Словарь-справочник терминов нормативно-технической документации
Статистическая значимость
Статистическая значимость часто применяется в маркетинге. С ее помощью определяют правильность выдвинутых предположений и вероятность их результатов. Она позволяет сделать выбор среди представленных теорий, что приводит к получению отличных результатов на практике.
Что такое статистическая значимость
Суть статистической значимости состоит в определении того, существует ли реальное основание в разнице между выбранными для исследования показателями, или это случайность? С данным понятием тесно связаны «нулевая» и «альтернативная» гипотезы.
Для лучшего понимания термина «статистическая значимость» необходимо понять, что такое «проверка гипотез». Эти два термина тесно взаимосвязаны.
Гипотеза иначе называется теорией. После окончания ее разработки требуется установить порядок по сбору достаточного количества доказательств этой теории и собрать их. Существует два типа гипотез: нулевая и альтернативная.
Нулевая гипотеза представляет собой теорию, которая гласит, что внесение коррективов ничего не поменяет, то есть сравниваемые объекты равнозначны в своих свойствах и нет смысла что-либо менять. Суть исследования заключается в опровержении гипотезы.
Альтернативная (исследовательская) гипотеза подразумевает сравнение, в результате которого один объект показывает себя эффективнее, чем другой.
Статистическая значимость как количественный показатель требует оценки. Оценка проходит поэтапно.
Постановка эксперимента
Все начинается с формулировки гипотезы. При этом должно быть выдвижение и нулевой, и альтернативной гипотезы. Придется сравнивать два набора данных для выяснения схожести и отличий. Эти утверждения требуют подтверждения с помощью экспериментальных данных.
Данный уровень представляет собой порог статистической значимости, который каждый устанавливает сам. Этот уровень носит название displaystyle \alpha >\alpha – уровня. Чаще всего, устанавливают значение в 0,05. Вероятность найти разницу составляет 5%. Чем выше уровень, тем достовернее результаты.
Когда нужна максимальная достоверность, стоит снизить значение с 0,05 до 0,01. Чаще всего, такие показатели применяют в производстве для выявления брака. Однако для большинства экспериментов достаточно значения в 0,05.
Решение об используемом критерии
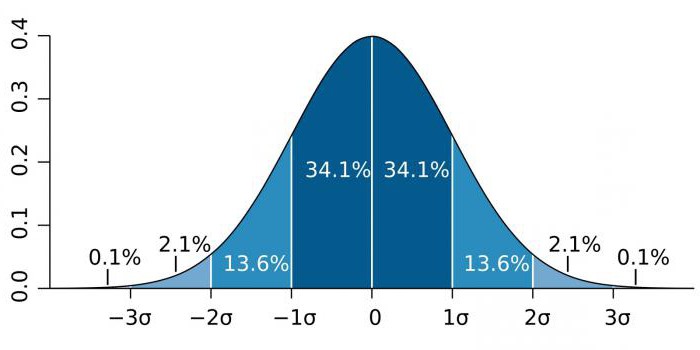
После установки уровня требуется определить, какой критерий использовать: одно- или двусторонний. Здесь стоит опираться на t-критерии Стьюдента. Они показывают, насколько нормально распределены данные. Графически они представлены в виде колоколообразной кривой. Большее количество результатов расположено в середине.
Критерий Стьюдента позволяет математически проверить расположены ли данные в установленных пределах или же выпадают из нормального распределения.
Двусторонний критерий нужен, когда нет уверенности в том, что показатели находятся выше или ниже установленной нормы распределения.
Когда есть точная уверенность, в каком направлении может наблюдаться выход за пределы нормы, нужно использовать односторонний критерий.
Определение объема выборки
Здесь потребуется статистическая мощность. Она представляет собой вероятность, что при выбранном объеме будет получен ожидаемый результат. Распространенный порог — 80%. Для анализа можно использовать специальные онлайн-калькуляторы. Это позволит определить оптимальный объем выборки.
Часто проводят пробное исследование, которое позволяет получить данные для анализа и установить объем выборки. Когда такой возможности нет, стоит поискать в тематической литературе усредненные значения.
Вычисление стандартного отклонения
Стандартное отклонение показывает величину разброса данных. Оно позволяет сделать выбор о близости или отдаленности данных. Их вычисляют по следующей формуле: s = √∑((xi – µ)2/(N – 1)).
s — стандартное отклонение;
∑ указывает на необходимость суммировать полученные данные по выборке;
xi соответствует значению i, то есть отдельному полученному результату;
µ — это среднее значение для данной группы;
N — общее число данных в выборке.
Теперь потребуется отыскать среднее значение для каждой группы. Для этого суммируют средние значения каждой группы и делят на объем выборки.
Далее необходимо определить разницу (xi – µ). Для этого следует вычесть из найденной средней величины каждое полученное значение.
Теперь каждую полученную величину умножают на саму себя или возводят во вторую степень и суммируют величины. После этой операции не должно остаться отрицательных значений.
Следующий шаг — деление объема минус один. Делят полученную в предыдущем шаге сумму на величину, полученную от вычитания единицы. После этого извлекают квадратный корень из величины. Это и будет нужная величина стандартного отклонения.
Определение значимости
Для определения значимости потребуется взять две группы данных. Для последней вычисляют стандартное отклонение, после чего вычисляют дисперсию между обеими группами по формуле:
sd — дисперсия между двумя группами;
s1 — стандартное отклонение в группе 1, N1 — объем выборки в группе 1;
s2 — стандартное отклонение в группе 2, N2 — объем выборки в группе 2.
Необходимо определить t-оценку показателей для перевода полученных данных в стандартизированную форму, которая позволить провести сравнение с другими данными. Эта оценка делает возможным проверку t-критерия, а также выяснение величины отличия одной группы от другой. Для определения t-оценки применяют формулу: t = (µ1 – µ2)/sd:
µ1 — среднее значение для первой группы;
µ2 — среднее значение для второй группы;
sd — дисперсия между двумя выборками.
Совет: первым используют большее среднее значение, чтобы итоговая величина не была отрицательной.
Далее требуется определить степень свободы выборки. Для этого вычисляют объем: суммируют объемы двух выборок и вычитают 2. Полученная величина станет окончательной. Ее оценивают по таблице значений критерия Стьюдента (t-критерия). Таблица представлена ниже.
Пользоваться представленной таблицей просто: находите строку в соответствии с полученной степенью свободы и определяете соответствующее t-оценке Р-значение.
Например, при степени свободы 8 и t-оценке 2,61 Р-значение для одностороннего критерия попадает между 0,01 и 0,025. При выбранном показателе в 0,05 эти данные попадают в категорию «статистически значимые». Это помогает сделать выбор в пользу альтернативной гипотезы и отказаться от нулевой.
Заключение
Определение статистической значимости помогает решать маркетинговые задачи и минимизировать риски. Такие расчеты часто проводятся при A/B тестированиях и помогают узнать, как будет вести себя клиент в будущем, окупится ли товар и т.д.
Что такое коэффициент значимости
Коэффициент значимости показателей качества продукции m в общем виде может быть определен отношением максимального количества баллов Б, установленного для данного 1-го показателя качества (свойства) продукции, к постоянному числу баллов (константа), принятому для всех свойств анализируемой группы изделия б [c.56]
Коэффициент значимости показателей качества продукции 56 [c.319]
Обработка на ЭВМ матриц экспертов по алгоритму, описанному в программе (приложение 2), завершается получением столбца коэффициентов значимости показателей. В условном примере при оценке значимости трех показателей получены следующие данные [c.74]
Результаты экспертной оценки могут быть более дифференцированными, чем в данном случае, где коэффициенты значимости показателей близки друг другу. [c.74]
Несмотря на относительную простоту использования этой модели для оценки финансового кризиса и угрозы банкротства, в наших экономических условиях она не позволяет получить достаточно объективный результат. Это вызывается различиями в учете отдельных показателей, влиянием инфляции на их формирование, несоответствием балансовой и рыночной стоимости отдельных активов и другими объективными причинами, которые определяют необходимость корректировки коэффициентов значимости показателей, приведенных в модели Альтмана, и учета ряда других показателей оценки кризисного развития предприятия. [c.248]
Определение весовых коэффициентов значимости показателей качества. Какие из выявленных ранее свойств товара потребители рассматривают как наиболее важные [c.293]
Формирование комплексного критерия сравнительной ценности проектов осуществляется следующим образом. Разрабатывается система частных показателей для оценки перспективности проекта. Формируется гипотетический набор проектов, в котором показатели варьируются на двух уровнях (наилучшие и наихудшие значения). На базе попарного сравнения полученных вариантов рассчитываются приоритеты проектов. Комплексный критерий перспективности проекта для отбора в план программы определяется суммированием произведений значений показателей и коэффициентов значимости показателей. Далее проекты ранжируются перспективности. В план программы включают проекты с наибольшими значениями комплексного критерия до исчерпания объема выделенных ресурсов. [c.373]
Показатели Оценка, баллы Коэффициент значимости Сумма баллов [c.68]
Пример. Определить степень выполнения плана социального развития коллектива предприятия на основе частных коэффициентов, характеризующих степень выполнения плана по отдельным показателям, и коэффициентов значимости показателен. В табл. 4.16 приведены исходные данные и расчет обобщающего показателя. [c.291]
Затем члены экспертной группы дали свои оценки относительной значимости каждой из пяти рассматривавшихся групп показателей. Эти оценки также были усреднены в целом по всей группе экспертов в виде весовых коэффициентов сравнительной значимости показателей каждой данной группы o j. И наконец, был рассчитан итоговый интегральный критерий эффективности проекта в целом [c.143]
По таблице характер связи Кк с Л, проследить трудно. Для наглядности данные перенесены на рис. 3.4. Графики показывают, что для октанового числа характерна почти линейная зависимость Кк и /0- Поэтому. вводить показатель степени ai в формулу (3.24) нет необходимости. Параметр Д (коэффициент значимости октанового числа) рассчитаем по данным табл. 3.4 решением уравнения [c.51]
Методы определения коэффициентов значимости единичных показателей уровня качества продукции [c.55]
Некоторые из приведенных формул дают хорошее приближение к истинной величине интегрального уровня качества при условии определения коэффициентов значимости единичных показателей на основе сопоставления базовой и итоговой функций полезности, как это было сделано в рассмотренных ранее примерах. Но проблема в том, что формальные способы синтеза Кк как раз и предназначены для тех случаев, когда функция полезности продукции неизвестна. Поэтому наиболее тяжелым и, в сущности, непреодолимым недостатком всех рассмотренных способов расчета Кк является необоснованность коэффициентов значимости ( Si) единичных показателей. [c.55]
В квалиметрии экспертный метод применяется непосредственно для определения уровня качества (продовольственных товаров, мебели, одежды), но чаще для установления коэффициентов значимости единичных показателей. В этом случае применяются из огромного множества вариантов техники проведения экспертного опроса в основном два индивидуальный и метод «Дельфы». [c.60]
При этом нет необходимости применять какие-либо коэффициенты значимости единичных показателей качества и произвольные формулы их синтеза в обобщенный, поскольку этот синтез осуществлен автоматически в ходе интегрального расчета удельных функций полезности изделия (Кц). [c.69]
Применяемая обычно стандартная математическая обработка экспертных оценок коэффициентов значимости (3, не гарантирует достоверность Кк, поскольку мнения экспертов встраиваются в заведомо упрощенную математическую структуру показателей (3.14), (3.15), (3.16), не соответствующую истинным взаимосвязям полезности продукции со значениями её частных свойств. [c.82]
Формула 4 является модификацией формулы 3. Она учитывает значимость показателей, определяемых экспертным путем. Необходимость введения весовых коэффициентов для отдельных показателей появляется при дифференциации оценки в соответствии с потребностями пользователей. [c.293]
Анализ параметров акций. Размер дивидендов по акциям и частота их выплат не дают реального представления о рыночной значимости выпускаемых обществом ценных бумаг, а свидетельствуют только об определенной дивидендной политике. Качественные параметры акций как финансовых инструментов можно проанализировать с помощью расчета ряда коэффициентов и показателей, успешно применяемых в зарубежной практике анализа и оценки акций. [c.350]
Надо заметить, что в целях получения более точной комплексной оценки любым из перечисленных методов может быть учтена сравнительная значимость показателей-индикаторов. Коэффициенты значимости, как правило, определяются экспертным путем. [c.45]
При использовании метода расстояний устанавливается близость объектов анализа — акционерных обществ, фирм, цехов, к объекту-эталону по каждому из сравниваемых показателей. Вначале определяются коэффициенты по каждому показателю как отношение его значения к показателю-эталону с максимальным уровнем. Затем рассчитывается сумма квадратов полученных коэффициентов. Если есть возможность учесть сравнительную значимость индикаторов, то каждый квадрат умножается на соответствующий весовой коэффициент значимости. Затем из суммы квадратов извлекается квадратный корень. [c.45]
Кроме того, Сбербанк РФ установил коэффициент значимости каждого показателя К — 0,11 KI — 0,05 К — 0,42 Кд — 0,21 KS — 0,21, т.е. наибольшая роль в определении кредитоспособности принадлежит таким показателям, как коэффициент общей ликвидности (0,45), коэффициент финансирования (0,21) и коэффициент рентабельности продаж (0,21). Порядок расчета общей суммы баллов ( w) осуществляется по средней арифметической взвешенной в табл. 10.2 [c.359]
Этап 3. Все элементы матрицы возводятся в квадрат. Если значимость показателей, составляющих матрицу, различна, тогда каждому показателю присваивается весовой коэффициент k, который определяется экспертным путем. [c.63]
Отмстим, что при использовании весовых коэффициентов значимости критериев результат может измениться. Например, если аналитик признает рентабельность самым важным показателем успешности деятельности предприятия, он может придать трем рассмотренным факторам веса (0,5 0,25 0,25), и тогда лучшим окажется предприятие № 3. [c.412]
Оценка технико-эстетического показателя качества с учетом поправочных коэффициентов значимости [c.73]
Для получения количественной оценки долгосрочной привлека-т льности рынка каждому показателю, характеризующему ее, следует определить нормированный весовой коэффициент (коэффициент значимости показателя среди других используемых менеджерами-исследователями при проведении анализа и выборе стратегии диверсификации). Сумма этих коэффициентов должна быть равна 1,0. Влияние каждого анализируемого показателя определяется как произведение коэффициента весомости на его балльную оценку, например на основе шкалы 1—5 баллов (табл. 5.17). [c.183]
Сказанное непременно следует учитывать при экспертизе многочисленных методик определения уровня качества, применяемых на предприятиях. Результаты проводимых экспертных опросов обставляются частоколом рангов, коэффициентов значимости, конкордации и т.п., что должно создавать иллюзию некой научной обоснованности. Причем значения е и а неправомерно интерпретируют как показатели точности и достоверности коэффициентов значимости частных показателей качества. Все это может пршзести к ошибочным [c.59]
При абсолютной согласованности мнений экспертов W=l. При W =0 коэффициенты значимости всех единичных показателей равны, а следовательно, мнения экспертов абсолютно несогласованы. При 0 0,35. [c.61]
Вывод о несогласованности мнений экспертов при W=0 является слабым местом показателя Кэндалла в частном случае, когда истинные значения коэффициентов весомости единичных показателей действительно равны или близки друг к другу. При равенстве истинных коэффициентов значимости может быть W
Уровень значимости в статистике
Уровень значимости в статистике является важным показателем, отражающим степень уверенности в точности, истинности полученных (прогнозируемых) данных. Понятие широко применяется в различных сферах: от проведения социологических исследований, до статистического тестирования научных гипотез.
Определение
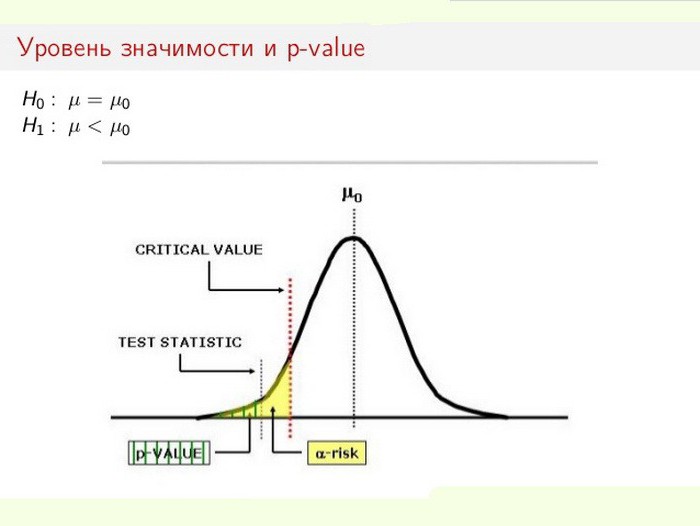
Уровень статистической значимости (или статистически значимый результат) показывает, какова вероятность случайного возникновения исследуемых показателей. Общая статистическая значимость явления выражается коэффициентом р-value (p-уровень). В любом эксперименте или наблюдении существует вероятность, что полученные данные возникли из-за ошибок выборки. Особенно это актуально для социологии.
То есть статистически значимой является величина, чья вероятность случайного возникновения крайне мала либо стремится к крайности. Крайностью в этом контексте считают степень отклонения статистики от нуль-гипотезы (гипотезы, которую проверяют на согласованность с полученными выборочными данными). В научной практике уровень значимости выбирается перед сбором данных и, как правило, его коэффициент составляет 0,05 (5 %). Для систем, где крайне важны точные значения, этот показатель может составлять 0,01 (1 %) и менее.
История вопроса
Понятие уровня значимости было введено британским статистиком и генетиком Рональдом Фишером в 1925 году, когда он разрабатывал методику проверки статистических гипотез. При анализе какого-либо процесса существует определенная вероятность тех либо иных явлений. Трудности возникают при работе с небольшими (либо не очевидными) процентами вероятностей, подпадающими под понятие «погрешность измерений».
При работе со статистическими данными, недостаточно конкретными, чтобы их проверить, ученые сталкивались с проблемой нулевой гипотезы, которая «мешает» оперировать малыми величинами. Фишер предложил для таких систем определить вероятность событий в 5 % (0,05) в качестве удобного выборочного среза, позволяющего отклонить нуль-гипотезу при расчетах.
Введение фиксированного коэффициента
В 1933 году ученые Ежи Нейман и Эгон Пирсон в своих работах рекомендовали заранее (до сбора данных) устанавливать определенный уровень значимости. Примеры использования этих правил хорошо видны во время проведения выборов. Предположим, есть два кандидата, один из которых очень популярен, а второй – малоизвестен. Очевидно, что первый кандидат выборы выиграет, а шансы второго стремятся к нулю. Стремятся – но не равны: всегда есть вероятность форс-мажорных обстоятельств, сенсационной информации, неожиданных решений, которые могут изменить прогнозируемые результаты выборов.
Нейман и Пирсон согласились, что предложенный Фишером уровень значимости 0,05 (обозначаемый символом α) наиболее удобен. Однако сам Фишер в 1956 году выступил против фиксации этого значения. Он считал, что уровень α должен устанавливаться в соответствии с конкретными обстоятельствами. Например, в физике частиц он составляет 0,01.
Значение p-уровня
Термин р-value впервые использован в работах Браунли в 1960 году. P-уровень (p-значение) является показателем, находящимся в обратной зависимости от истинности результатов. Наивысший коэффициент р-value соответствует наименьшему уровню доверия к произведенной выборке зависимости между переменными.
Данное значение отражает вероятность ошибок, связанных с интерпретацией результатов. Предположим, p-уровень = 0,05 (1/20). Он показывает пятипроцентную вероятность того, что найденная в выборке связь между переменными – всего лишь случайная особенность проведенной выборки. То есть, если эта зависимость отсутствует, то при многократных подобных экспериментах в среднем в каждом двадцатом исследовании можно ожидать такую же либо большую зависимость между переменными. Часто p-уровень рассматривается в качестве «допустимой границы» уровня ошибок.
Кстати, р-value может не отражать реальную зависимость между переменными, а лишь показывает некое среднее значение в пределах допущений. В частности, окончательный анализ данных будет также зависеть от выбранных значений данного коэффициента. При p-уровне = 0,05 будут одни результаты, а при коэффициенте, равном 0,01, другие.
Проверка статистических гипотез
Уровень статистической значимости особенно важен при проверке выдвигаемых гипотез. Например, при расчетах двустороннего теста область отторжения разделяют поровну на обоих концах выборочного распределения (относительно нулевой координаты) и высчитывают истинность полученных данных.
Предположим, при мониторинге некоего процесса (явления) выяснилось, что новая статистическая информация свидетельствует о небольших изменениях относительно предыдущих значений. При этом расхождения в результатах малы, не очевидны, но важны для исследования. Перед специалистом встает дилемма: изменения реально происходят или это ошибки выборки (неточность измерений)?
Эффективность
Необходимо учитывать, что коэффициенты α и р-value не являются точными характеристиками. Каким бы ни был уровень значимости в статистике исследуемого явления, он не является безусловным основанием для принятия гипотезы. Например, чем меньше значение α, тем больше шанс, что устанавливаемая гипотеза значима. Однако существует риск ошибиться, что уменьшает статистическую мощность (значимость) исследования.
Исследователи, которые зацикливаются исключительно на статистически значимых результатах, могут получить ошибочные выводы. При этом перепроверить их работу затруднительно, так как ими применяются допущения (коими фактически и являются значения α и р-value). Поэтому рекомендуется всегда, наряду с вычислением статистической значимости, определять другой показатель – величину статистического эффекта. Величина эффекта – это количественная мера силы эффекта.