Что такое изометрия детали

Аксонометрические проекции

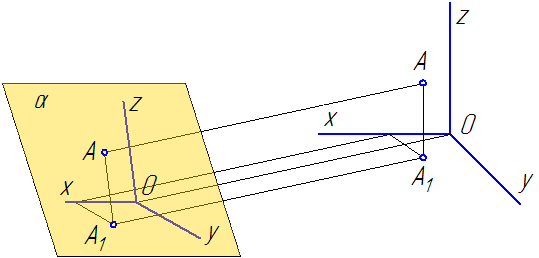
Способ аксонометрического проецирования состоит в том, что данный предмет вместе с осями прямоугольных координат, к которым эта система относится в пространстве, параллельно проецируется на некоторую плоскость α (Рисунок 4.1).

Рисунок 4.1
Направление проецирования S определяет положение аксонометрических осей на плоскости проекций α, а также коэффициенты искажения по ним. При этом необходимо обеспечить наглядность изображения и возможность производить определения положений и размеров предмета.
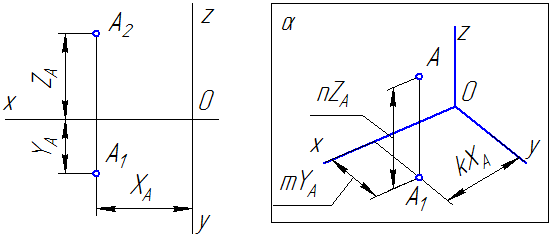
В качестве примера на Рисунке 4.2 показано построение аксонометрической проекции точки А по ее ортогональным проекциям.

Рисунок 4.2
Здесь буквами k, m, n обозначены коэффициенты искажения по осям OX, OY и OZ соответственно. Если все три коэффициента равны между собой, то аксонометрическая проекция называется изометрической, если равны между собой только два коэффициента, то проекция называется диметрической, если же k≠m≠n, то проекция называется триметрической.
Если направление проецирования S перпендикулярно плоскости проекций α, то аксонометрическая проекция носит названия прямоугольной. В противном случае, аксонометрическая проекция называется косоугольной.
ГОСТ 2.317-2011 устанавливает следующие прямоугольные и косоугольные аксонометрические проекции:

Ниже приводятся параметры только трех наиболее часто применяемых на практике аксонометрических проекций.
Каждая такая проекция определяется положением осей, коэффициентами искажения по ним, размерами и направлениями осей эллипсов, расположенных в плоскостях, параллельных координатным плоскостям. Для упрощения геометрических построений коэффициенты искажения по осям, как правило, округляются.

4.1. Прямоугольные проекции

4.1.1. Изометрическая проекция

Направление аксонометрических осей приведено на Рисунке 4.3.

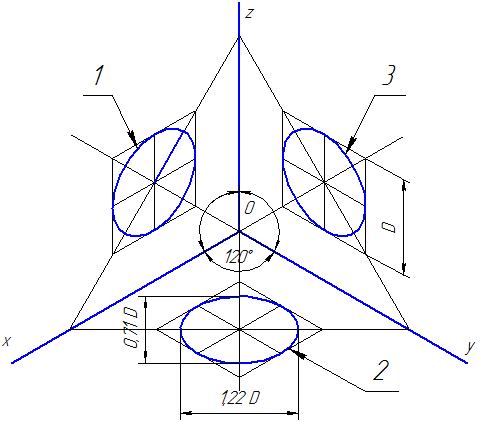
Рисунок 4.3 – Аксонометрические оси в прямоугольной изометрической проекции

Действительные коэффициенты искажения по осям OX, OY и OZ равны 0,82. Но с такими значениями коэффициентов искажения работать не удобно, поэтому, на практике, используются приведенные коэффициенты искажений. Эта проекция обычно выполняется без искажения, поэтому, приведенные коэффициенты искажений принимается k = m = n =1. Окружности, лежащие в плоскостях, параллельных плоскостям проекций, проецируются в эллипсы, большая ось которых равна 1,22, а малая – 0,71 диаметра образующей окружности D.

Большие оси эллипсов 1, 2 и 3 расположены под углом 90º к осям OY, OZ и OX, соответственно.

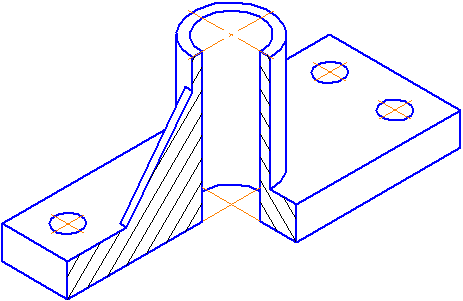
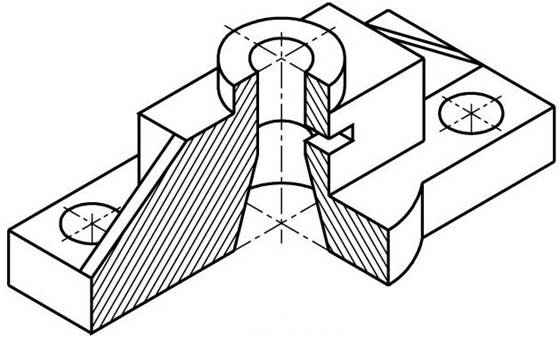
Пример выполнения изометрической проекции условной детали с вырезом приводится на Рисунке 4.4.

Рисунок 4.4 – Изображение детали в прямоугольной изометрической проекции

4.1.2. Диметрическая проекция

Положение аксонометрических осей проводится на Рисунке 4.5.

Для построения угла, приблизительно равного 7º10´, строится прямоугольный треугольник, катеты которого составляют одну и восемь единиц длины; для построения угла, приблизительно равного 41º25´ — катеты треугольника, соответственно, равны семи и восьми единицам длины.

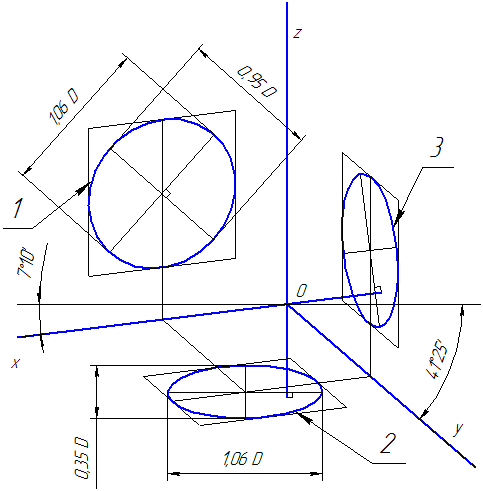
Коэффициенты искажения по осям ОХ и OZ k=n=0,94 а по оси OY – m=0,47. При округлении этих параметров принимается k=n=1 и m=0,5. В этом случае размеры осей эллипсов будут: большая ось эллипса 1 равна 0,95D и эллипсов 2 и 3 – 0,35D (D – диаметр окружности). На Рисунке 4.5 большие оси эллипсов 1, 2 и 3 расположены под углом 90º к осям OY, OZ и OX, соответственно.

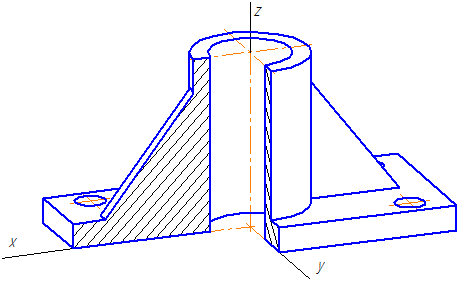
Пример прямоугольной диметрической проекции условной детали с вырезом приводится на Рисунке 4.6.

Рисунок 4.5 – Аксонометрические оси в прямоугольной диметрической проекции

Рисунок 4.6 – Изображение детали в прямоугольной диметрической проекции

4.2 Косоугольные проекции

4.2.1 Фронтальная диметрическая проекция

Коэффициент искажения по оси OY равен m=0,5 а по осям OX и OZ — k=n=1.

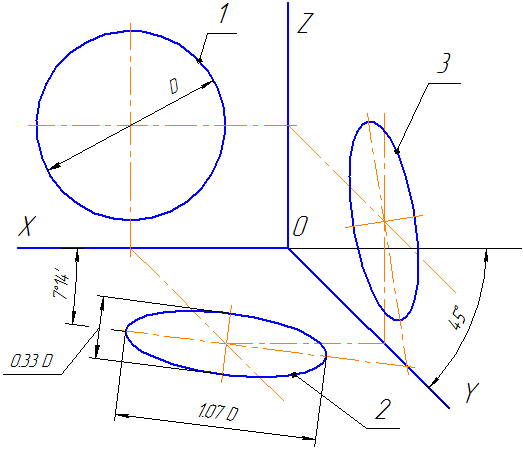
Рисунок 4.7 – Аксонометрические оси в косоугольной фронтальной диметрической проекции

Окружности, лежащие в плоскостях, параллельных фронтальной плоскости проекций, проецируются на плоскость XOZ без искажения. Большие оси эллипсов 2 и 3 равны 1,07D, а малая ось – 0,33D (D — диаметр окружности). Большая ось эллипса 2 составляет с осью ОХ угол 7º 14´, а большая ось эллипса 3 составляет такой же угол с осью OZ.

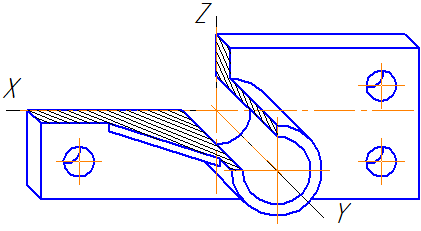
Пример аксонометрической проекции условной детали с вырезом приводится на Рисунке 4.8.

Как видно из рисунка, данная деталь располагается таким образом, чтобы её окружности проецировались на плоскость XОZ без искажения.

Рисунок 4.8 – Изображение детали в косоугольной фронтальной диметрической проекции

4.3 Построение эллипса

4.3.1 Построения эллипса по двум осям

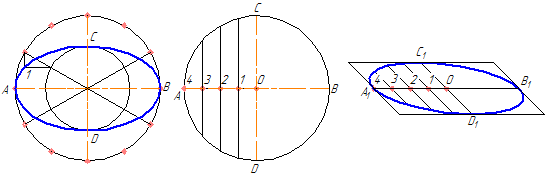
На данных осях эллипса АВ и СD строятся как на диаметрах две концентрические окружности (Рисунок 4.9, а).

Одна из этих окружностей делится на несколько равных (или неравных) частей.

Через точки деления и центр эллипса проводятся радиусы, которые делят также вторую окружность. Затем через точки деления большой окружности проводятся прямые, параллельные линии АВ.

Точки пересечения соответствующих прямых и будут точками, принадлежащими эллипсу. На Рисунке 4.9, а показана лишь одна искомая точка 1.

а б в
Рисунок 4.9 – Построение эллипса по двум осям (а), по хордам (б)

4.3.2 Построение эллипса по хордам

Диаметр окружности АВ делится на несколько равных частей, на рисунке 4.9,б их 4. Через точки 1-3 проводятся хорды параллельно диаметру CD. В любой аксонометрической проекции (например, в косоугольной диметрической) изображаются эти же диаметры с учетом коэффициента искажения. Так на Рисунке 4.9,б А₁В₁=АВ и С₁ D₁ = 0,5CD. Диаметр А ₁В₁ делится на то же число равных частей, что и диаметр АВ, через полученные точки 1-3 проводятся отрезки, равные соответственным хордам, умноженным на коэффициент искажение (в нашем случае – 0,5).

4.4 Штриховка сечений

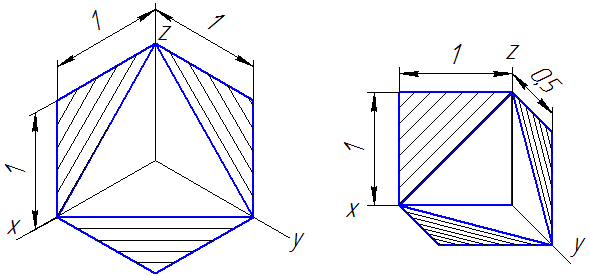
Линии штриховки сечений (разрезов) в аксонометрических проекциях наносятся параллельно одной из диагоналей квадратов, лежащих в соответствующих координатных плоскостях, стороны которых параллельны аксонометрическим осям (Рисунок 4.10: а – штриховка в прямоугольной изометрии; б – штриховка в косоугольной фронтальной диметрии).

а б
Рисунок 4.10 – Примеры штриховки в аксонометрических проекциях

Источник

Что такое изометрия детали

Аксонометрические проекции применяются в качестве вспомогательных к чертежам в тех случаях, когда требуется поясняющее наглядное изображение формы детали. В ГОСТ 2.317-69 стандартизованы прямоугольные и косоугольные аксонометрические проекции с различным расположением осей.

ПРЯМОУГОЛЬНЫЕ ПРОЕКЦИИ

Изометрическая проекция

Линии штриховки сечений в аксонометрических проекциях наносят параллельно одной из диагоналей проекций квадратов, лежащих в соответствующих координатных плоскостях, стороны которых параллельны аксонометрическим осям. Для изометрической проекции вариант штриховки по плоскостям приведен на рис. 2.

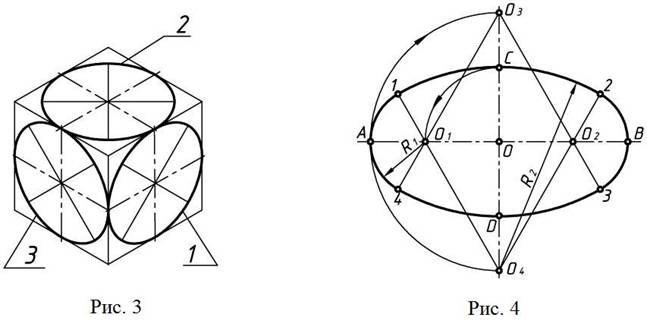
Окружности, лежащие в плоскостях, параллельных плоскостям проекций, проецируются на аксонометрическую плоскость проекций в эллипсы (рис. 3).

Построение эллипсов в изометрической проекции окружности можно заменить построением овалов, Следует отметить, что очертание любого циркульного овала не совпадает с очертанием эллипса, имеющего такие же оси, хотя и приближается к нему. Один из способов построения овала приведен на рис. 4.

Пример изображения детали в прямоугольной изометрии приведен на рис. 5.

Диметрическая проекция

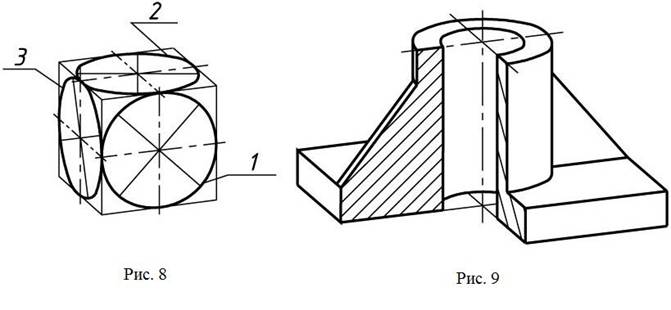
Штриховка сечений в прямоугольной диметрической проекции показана на рис.7, а пример изображения детали – на рис. 9.

Окружности, лежащие в плоскостях, параллельных плоскостям проекций, проецируются на аксонометрическую плоскость проекций в эллипсы (рис. 8).

КОСОУГОЛЬНЫЕ ПРОЕКЦИИ

Фронтальная изометрическая проекция

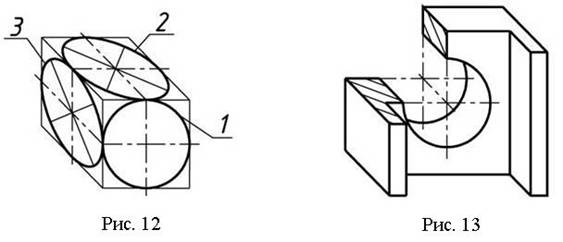
Штриховка сечений в косоугольной фронтальной изометрической проекции показана на рис. 11, а пример выполнения изображения детали – на рис.13.

Окружности, лежащие в плоскостях, параллельных фронтальной плоскости проекций, проецируются на аксонометрическую плоскость в окружности, а окружности, лежащие в плоскостях, параллельных горизонтальной и профильной плоскостям проекций, – в эллипсы (рис. 12).

Горизонтальная изометрическая проекция

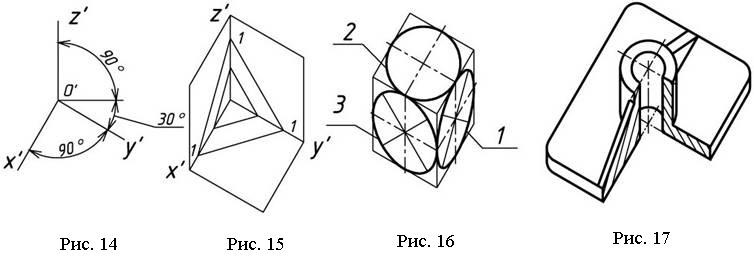
Штриховка сечений в косоугольной горизонтальной изометрической проекции показана на рис.15, а пример изображения детали – на рис. 17.

Окружности, лежащие в плоскостях, параллельных горизонтальной плоскости проекций, проецируются на аксонометрическую плоскость проекций в окружности, а окружности, лежащие в плоскостях, параллельных фронтальной и профильной плоскостям проекций, – в эллипсы (рис.16).

Фронтальная диметрическая проекция

Штриховка сечений в косоугольной фронтальной диметрии показана на рис.19, а пример изображения детали – на рис.21

Источник

Изометрическая проекция

Изометри́ческая прое́кция — это разновидность аксонометрической проекции, при которой в отображении трёхмерного объекта на плоскость коэффициент искажения (отношение длины спроектированного на плоскость отрезка, параллельного координатной оси, к действительной длине отрезка) по всем трём осям один и тот же. Слово «изометрическая» в названии проекции пришло из греческого языка и означает «равный размер», отражая тот факт, что в этой проекции масштабы по всем осям равны. В других видах проекций это не так.

Изометрическая проекция используется в машиностроительном черчении и САПР для построения наглядного изображения детали на чертеже, а также в компьютерных играх для трёхмерных объектов и панорам.

Содержание

Стандартные изометрические проекции [1]

Прямоугольная (ортогональная) изометрическая проекция

В прямоугольной изометрической проекции аксонометрические оси образуют между собой углы в 120°, ось Z’ направлена вертикально. Коэффициенты искажения () имеют числовое значение . Как правило, для упрощения построений изометрическую проекцию выполняют без искажений по осям, то есть коэффициент искажения принимают равным 1, в этом случае получают увеличение линейных размеров в раза.

Косоугольная фронтальная изометрическая проекция

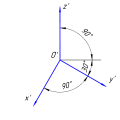
Ось Z’ направлена вертикально, угол между осью X’ и Z’ равен 90°, ось Y’ с углом наклона 135° (допускается 120° и 150°) от оси Z’.

Фронтальная изометрическая проекция выполняется по осям X’, Y’ и Z’ без искажения.

Кривые параллельные фронтальной плоскости проецируются без искажений.

Косоугольная горизонтальная изометрическая проекция

Ось Z’ направлена вертикально, между осью Z’ и осью Y’ угол наклона равен 120° (допускается 135° и 150°), при этом сохраняется угол между осями X’ и Y’ равным 90°.

Горизонтальную изометрическую проекцию выполняют без искажения по осям X’, Y’ и Z’.

Кривые, параллельные горизонтальной плоскости [2] проецируются без искажений.

Визуализация

Изометрический вид объекта можно получить, выбрав направление обзора таким образом, чтобы углы между проекцией осей x, y, и z были одинаковы и равны 120°. К примеру, если взять куб, это можно выполнить направив взгляд на одну из граней куба, после чего повернув куб на ±45° вокруг вертикальной оси и на ±arcsin (tan 30°) ≈ 35.264° вокруг горизонтальной оси. Обратите внимание: на иллюстрации изометрической проекции куба контур проекции образует правильный шестиугольник — все рёбра равной длины и все грани равной площади.

Подобным же образом изометрический вид может быть получен, к примеру, в редакторе трёхмерных сцен: начав с камерой, выровненной параллельно полу и координатным осям, её нужно повернуть вниз на ≈35.264° вокруг горизонтальной оси и на ±45° вокруг вертикальной оси.

Другой путь визуализации изометрической проекции заключается в рассмотрении вида кубической комнаты с верхнего угла с направлением взгляда в противолежащий нижний угол. Ось x здесь направлена диагонально вниз и вправо, ось y — диагонально вниз и влево, ось z — прямо вверх. Глубина также отражается высотой картинки. Линии, нарисованные вдоль осей, имеют угол 120° между собой.

Матричные преобразования

Имеется 8 различных вариантов получения изометрической проекции в зависимости от того, в какой октант смотрит наблюдатель. Изометрическое преобразование точки в трёхмерном пространстве в точку на плоскости при взгляде в первый октант может быть математически описано с помощью матриц поворота следующим образом. Вначале, как объяснено в разделе Визуализация, выполняется поворот вокруг горизонтальной оси (здесь x) на α = arcsin (tan 30°) ≈ 35.264° и вокруг вертикальной оси (здесь y) на β = 45°:

Затем применяется ортогональная проекция на плоскость x-y:

Другие семь возможных видов получаются поворотом к противостоящим сторонам и/или инверсией направления взгляда. [3]

Ограничения аксонометрической проекции

Как и в других видах параллельных проекций, объекты в аксонометрической проекции не выглядят больше или меньше при приближении или удалении от наблюдателя. Это полезно в архитектурных чертежах и удобно в спрайто-ориентированных компьютерных играх, но, в отличие от перспективной (центральной) проекции, приводит к ощущению искривления, поскольку наши глаза или фотография работают иначе.

Это также легко приводит к ситуациям, когда глубину и высоту невозможно оценить, как показано на иллюстрации справа. В этом изометрическом рисунке голубой шар на два уровня выше красного, но это нельзя увидеть, если смотреть только на левую половину картинки. Если выступ, на котором находится голубой шар, расширить на один квадрат, то он окажется точно рядом с квадратом, на котором находится красный шар, создавая оптическую иллюзию, будто оба шара на одном уровне.

Дополнительная проблема, специфичная для изометрической проекции — сложность определения, какая сторона объекта наблюдается. При отсутствии теней и для объектов, которые относительно перпендикулярны и соразмерны, сложно определить, какая сторона является верхней, нижней или боковой. Это происходит из-за приблизительно равных по размеру и площади проекций такого объекта.

Большинство современных компьютерных игр избегают этого за счёт отказа от аксонометрической проекции в пользу перспективного трёхмерного рендеринга. Однако эксплуатация проекционных иллюзий популярна в оптическом искусстве — таком, как работы из серии «невозможной архитектуры» Эшера. Водопад (1961) — хороший пример, в котором строение в основном изометрическое, в то время как блеклый фон использует перспективную проекцию. Другое преимущество заключается в том, что в черчении даже новички легко могут строить углы в 60° с помощью только циркуля и линейки.

Изометрическая проекция в компьютерных играх и пиксельной графике

В области компьютерных игр и пиксельной графики аксонометрическая проекция была весьма популярна в силу лёгкости, с которой двухмерные спрайты и плиточная графика (англ.) могли быть использованы для представления трёхмерной игровой среды — поскольку во время перемещения по игровому полю объекты не меняют размер, компьютеру не требуется масштабировать спрайты или выполнять вычисления, необходимые для моделирования визуальной перспективы. Это позволяло старым 8-битным и 16-битным игровым системам (и, позднее, портативным игровым системам) легко отображать большие трёхмерные пространства. И хотя неразбериха с глубиной (см. выше) иногда могла быть проблемой, хороший дизайн игры способен её смягчить. С приходом более мощных графических систем аксонометрическая проекция стала терять свои позиции.

Проекция в компьютерных играх обычно несколько отличается от «истинной» изометрической в силу ограничений растровой графики — линии по осям x и y не имели бы аккуратного пиксельного узора, если бы рисовались под углом в 30° к горизонтали. Хотя современные компьютеры могут устранять эту проблему с помощью сглаживания, ранее компьютерная графика не поддерживала достаточную цветовую палитру или не располагала достаточной мощностью процессоров для его выполнения. Вместо этого использовалась пропорция пиксельного узора 2:1 для рисования осевых линий x и y, в результате чего эти оси располагались под углом arctan 0,5 ≈ 26,565° к горизонтали. (Игровые системы с неквадратными пикселями могли, однако, приводить к другим углам, включая полностью изометрические). Поскольку здесь из трёх углов между осями (116,565°, 116,565°, 126,87°) равны только два, такой вид проекции более точно характеризуется как вариация диметрической проекции. Однако большинство представителей сообществ компьютерных игр и растровой графики продолжает называть эту проекцию «изометрической перспективой». Также, часто используются термины «вид 3/4 (англ.)» и «2.5D».

История изометрических компьютерных игр

На протяжении 1990-х некоторые очень успешные игры вроде Civilization II и Diablo использовали фиксированную изометрическую перспективу. С приходом 3D ускорителей на персональные компьютеры и игровые консоли игры с трёхмерной перспективой в основном переключились на полноценную трёхмерность вместо изометрической перспективы. Это можно видеть в преемницах вышеназванных игр — начиная с Civilization IV в этой серии используется полная трёхмерность. Diablo II, как и ранее, использует фиксированную перспективу, но опционально применяет перспективное масштабирование спрайтов на расстоянии, получая псевдо-трёхмерную перспективу. [18]

Источник

Понятие об аксонометрических проекциях

Наглядные изображения применяют для пояснения чертежей деталей и машин. По ним легче представить форму предмета, чем по чертежу в трёх видах.

Одним из видов наглядных изображений являются аксонометрические изображения.

Аксонометрия в переводе с греческого означает «измерение по осям».

Аксонометрические проекции получают путём проецирования параллельными лучами

предмета, который связан с осями прямоугольных координат, на некоторую плоскость Р (рис. 103).

Таким образом, аксонометрическая проекция – это проекция только на одну плоскость.

Чтобы изображение получилось наглядным, проецирующие лучи не должны быть параллельны ни одной оси координат. Тогда на плоскости Р будут, хоть и с искажениями, изображены все три измерения предмета.

Аксонометрические проекции в зависимости от направления проецирования делятся на два вида: прямоугольные, когда направление проецирования перпендикулярно плоскости Р (угол φ=90°), и косоугольные, когда угол φ≠90°.

Если плоскость Р не параллельна ни одной из координатных плоскостей x,y,z, то на аксонометрической проекции у предмета искажаются все три его измерения. Если же плоскость Р параллельна одной или двум осям координат, то у предмета искажаются размеры соответственно по двум его измерениям или по одному.

Величина искажения определяется коэффициентом искажения, который равен отношению длины аксонометрической проекции отрезка, параллельного соответствующей оси координат, к его действительной длине. Любая аксонометрическая проекция имеет три коэффициента искажения по числу осей координат.

В зависимости от того, разные они или одинаковые, аксонометрические проекции делят на изометрические (коэффициенты искажения равны по всем трём осям) и триметрические (коэффициенты искажения по всем осям разные).

Стандартные виды аксонометрии. Изометрия. Диметрия

Наиболее распространёнными видами аксонометрических проекций являются прямоугольная изометрическая проекция (изометрия) и прямоугольная диметрическая проекция (диметрия), основные правила построения которых определены стандартом.

Прямоугольная изометрия представляет собой аксонометрическую проекцию с направлением проецирования, перпендикулярным к плоскости аксонометрических проекций одинаковыми по всем трём осям коэффициентами искажения, равными 0,82.

Оси изометрии (рис. 104а) составляют между собой углы 120°. Ось Z расположена вертикально. Для упрощения построения коэффициент искажения принимают равным 1.

Изображение при этом получается увеличенным, но вид его не меняется, т.к. сохраняется пропорциональность всех его размеров.

На рис. 104б и в приведены два способа построения осей в изометрии.

Прямоугольная диметрия представляет собой аксонометрическую проекцию с направлением проецирования, перпендикулярным аксонометрической плоскости проекций Р и одинаковыми коэффициентами искажения по осям х и z.

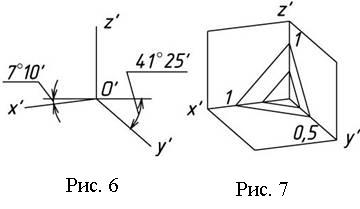
Ось х (рис. 105а) составляет с горизонтальной прямой угол 7°10′, а ось у – угол 41°25′.

Ось z занимает вертикальное положение. На рис. 105б показан графический способ построения осей диметрии.

В диметрии коэффициенты искажения по осям х и z равны 0,94, а по оси у – 0,47. При построениях первый коэффициент округляют до 1, а второй – до 0,5. Таким образом, отрезки, параллельные осям координат х и z, откладывают в натуральную величину, а длину отрезков, параллельных оси у, уменьшают в два раза.

Построение окружности в аксонометрии

Изометрия. Изометрические проекции окружностей, расположенных в плоскостях проекций или в плоскостях, им параллельных, есть эллипсы (рис. 106).

Большие оси этих эллипсов равны l,22Dокр, а малые 0,71Dокр, где Dокр – диаметр изображаемой окружности. Большая ось эллипсов всегда перпендикулярна к той аксонометрической оси, которая отсутствует в плоскости окружности, а малая совпадает с этой осью или параллельна ей.

Практически при построении изометрии окружности эллипс обычно заменяют близким к нему по форме овалом, т.к. построение овала значительно проще.

Наиболее простой способ построения овала показан на рис. 107.

На рис. 108а,б построены изометрии окружностей, расположенных во фронтальной и профильной плоскостях.

Окружности, расположенные во фронтальной плоскости, проецируются в виде эллипсов с большой осью, равной 1,06Dокр, а малой – 0,94Dокр. Большие оси эллипсов, как и в изометрии, перпендикулярны к той аксонометрической оси, которая отсутствует в данной плоскости, а малые оси совпадают с направлением этой оси.

Диметрии окружностей (эллипсы) обычно заменяют овалами, размеры осей которых равны размерам соответствующих осей эллипсов. Построение этих овалов показано на рис. 110. На рис. 110а построения понятны по чертежу.

На рис. 110б строим оси диметрии х_р, у_р, z_р. Затем строим прямую, перпендикулярную оси у_р. Отложив на осях х_р и z_р радиус заданной окружности, получим точки М, К, N, L, которые являются точками сопряжения дуг овала. Через точки М и N проводим горизонтальные прямые. В пересечении этих прямых с осью у_р и перпендикуляром к ней получим точки О₁, О₂, О₃, О₄. Из центров O₁ и О₃ опишем дуги радиусом R₁=О₃ K, а из центров О₂ и О₄ – дуги радиусом R₂=О₂M.

Аксонометрические изображения предметов

Приступая к построению аксонометрической проекции предмета, следует выбрать вид аксонометрии, обеспечивающий наибольшую наглядность изображения. Затем предмет связывают с системой прямоугольных координат, оси которой обычно совмещают с осями симметрии предмета. Только после этого можно приступить к построению аксонометрии.

Построение аксонометрии предмета обычно начинают с построения аксонометрии одной из его проекций (вторичной проекции). Затем полученное изображение дополняют построением третьего измерения всех его точек.

На рис. 111 показан пример построения прямоугольной изометрии предмета через построение его горизонтальной проекции.

На рис. 112 приведен пример построения прямоугольной изометрии детали путём построения её вторичной фронтальной проекции.

Для выявления внутренней формы предмета, изображённого в аксонометрии, в некоторых случаях применяют разрезы, которые условно называют вырезами. При этом используют две секущие плоскости, обычно совпадающие с плоскостями симметрии предмета (рис. 113).

рис. 111 рис. 112 рис. 113

Линии штриховки сечений в аксонометрических проекциях наносят параллельно одной из диагоналей проекций квадратов, лежащих в соответствующих координатных плоскостях. Стороны квадратов параллельны аксонометрическим осям (рис. 114).

Источник