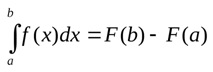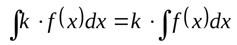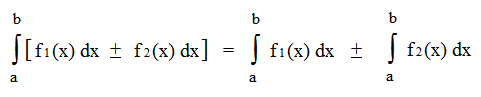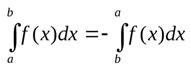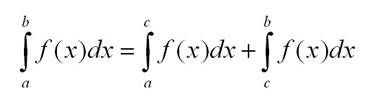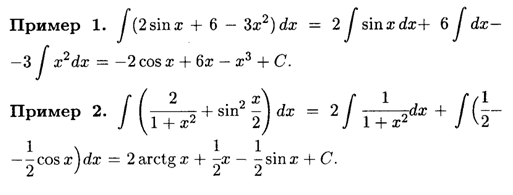Что такое интеграл в математике простыми словами кратко и ясно
Что такое Интеграл
Интеграл — это математическая концепция, которая может быть двух типов:
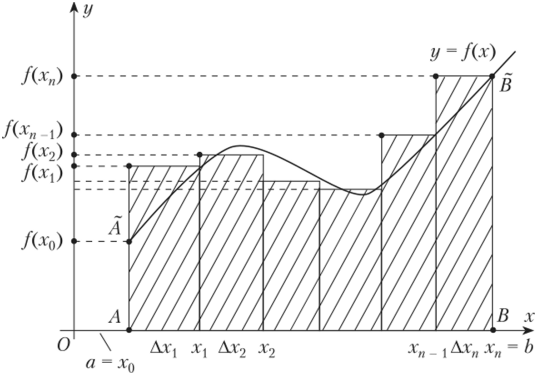
Определённый интеграл выражает область под кривой графика неотрицательной функции f между любыми двумя значениями a и b, как показано на этом рисунке:
Интеграл, определённый между a и b, представлен как: 
Неопределённый интеграл функции f — это другая функция F, полученная процессом, противоположным дифференцированию.
Дифференцирование в математике — это процесс, который превращает функцию f в другую функцию f’, называемую производной от f.
Например, нужно найти производную функции f(x) = cos x:
Обозначение интеграла
Знак определённого интеграла:
Знак неопределённого интеграла: ∫
Основные свойства интегралов
Решение интегралов
Первообразная функция
Это функция, у которой производная функция равна исходной.
Функция F(x) является первообразной для производной функции f(x), если выполняется равенство F'(x) = f(x) (в диапазоне I).
Важная деталь, о которой нужно помнить: первообразные функции не являются единственными! В предыдущем примере первообразная функции 3x² равна x³, но x³ + 1 также является первообразной той же функции (3x²), потому что (x³ + 1)’= 3x².
Это означает, что неопределённый интеграл функции f является множеством всех её первообразных функций и представлен так:
где С — произвольная постоянная.
Неопределённый интеграл
Неопределённый интеграл выглядит примерно так ∫ f(x) d(x) и обозначает множество всех первообразных некоторой функции f(x).
Если F — некоторая частная первообразная, то:
где С — произвольная постоянная.
Например, нужно вычислить неопределённый интеграл:
∫ (2x – 1) dx = ∫2x dx – ∫1dx = 2 (x²/2) – x + C = x² – x + C.
Определённый интеграл
Определённый интеграл выглядит примерно так: 
С помощью определённого интеграла можно вычислить площадь геометрической фигуры, которая находится под кривой. Отрезок [a;b] называется отрезком интегрирования. Вместо a и b подставляются значения X (минимального и максимального). Например, как на этом рисунке:
Решение определённого интеграла (формула Ньютона-Лейбница):

Например, нужно вычислить определённый интеграл:

1) Вычислить первообразную функцию
∫ (2 – x – x²) dx = 2x – x²/2 – x³/3 + C
2) Рассчитать верхний и нижний пределы (разницу между максимальным и минимальным значениями):


Значит, площадь того, что закрашено на рисунке (под графиком), будет равна 4,5.
Интеграл простыми словами
Интегралы начинают изучать еще в школе. Но никто из учителей не говорит, зачем это нужно, как использовать эти знания в жизни. Мало кто вообще способен объяснить простыми словами, что такое интеграл, даже в университете. А мы попробуем.
Простыми словами…
Если коротко — интеграл, это сумма маленьких частей. Да, точно так же как и сложение 2+2, только части бесконечно маленькие, естественно и количество их — бесконечно.
Знак интеграла ∫ — это вытянутая буква s (длинная «эс» существовала до начала 19-ого века писалась так — ſ). Первая буква слова summa.
Интегрирование — это сложение бесконечного количества частей бесконечно маленького значения.
Почему обычного «плюсования» не достаточно? Просто в алгебре нет никаких бесконечно малых или больших.
Бесконечно малая величина, это не какое-то конкретное число. Это абстракция, в реальном мире аналогов просто нет. Мы придумали так для удобства. Что-то настолько маленькое, что измерять его бессмысленно, но в расчетах использовать можно.
Слово «интеграл» происходит от латинского integer, что означает «целый». Даже в названии есть намек некое действие, что-то вроде восстановления чего-то целого.
Лучше всего показать «на пальцах», точнее на примере. Предположим, мы хотим узнать площадь фигуры как на картинке (она называется криволинейная трапеция, потому, что одна из сторон создана кривой линией). Зачем нам это нужно? Например, это часть крыла самолета и нужно знать его площадь.
Можно, конечно, разбить фигуру на две, прямоугольник и треугольник.
Но останется «пробел», площадь которого будет неизвестна. Чтобы увеличить точность, можно разделять на большее количество фигур, но все равно будет оставаться какая-то, пусть и небольшая, но «не закрашенная» область. Фигуры будут становиться все меньше и меньше… Очевидно, что процесс измельчения будет бесконечным, по крайней мере в воображении.
Но, в реальности, бесконечный процесс попросту не нужен. На самом деле вычислить такие вещи как площадь круга, длину диагонали квадрата или объем пирамиды невозможно, значение будет бесконечным, естественно, практического смысла бесконечные числа не имеют и мы их «округляем» до нужного предела точности — приблизительно.
Такой метод в Древней Греции назывался «исчерпание». Аналогия с водой тут очень уместна, если представить, что черпаешь из ведра при помощи кружки, то сначала кружки будут полные, но чем ближе ко дну, тем меньший объем будет попадать в кружку. Первой известной личностью «взявшей интеграл» был Архимед, он фактически решил задачу по нахождению площади круга и площади параболы ничего не зная ни про пределы, но даже про число «пи».
Чем больше будет фигур, тем больше будет и точность расчета и тем меньше будут сами фигурки. Если площадь маленьких фигурок будет бесконечно малой, то есть стремится к нулю (но не равняться ему), сумма всех этих площадей будет равна сумме большой фигуры с бесконечно большой точностью.
То же самое происходит при интегрировании:
Фигура на картинке разбивается на столбцы бесконечно маленькой ширины. Ширина у нас Х. Бесконечно малое число обозначается d. То есть dx — это бесконечно малый «икс».
Сложение бесконечного числа частей бесконечно маленького размера это и есть интегрирование.
Чтобы узнать площадь фигуры нужна еще высота, а это y. Высота везде не одинаковая, она постоянно меняется. И мы знаем как именно! Ведь кривая может быть (а может и не быть, но в нашем случае так и есть) функцией y=f(x), то есть значение у меняется по закону (буква f об этом говорит) зависимому от х. Поэтому «эф от икс». Значит высота это f(x). Функция, кстати, тоже бесконечная.
Высота конкретного прямоугольничка, это значение функции в этой конкретной точке (почему точке, потому, что ширина полоски у нас бесконечно маленькая, мы так договорились в самом начале).
Площадь, это высота умноженная на ширину. За высоту можем брать и y и f(x), они равны. За ширину у нас играет dx. Итак, момент истины:
f(x)dx — площадь нашего маленького столбика. В если собрать из все вместе, будет сумма бесконечно маленьких столбиков.
А площадь нужна не бесконечной фигуры, а той что начинается от 1 и закачивается на 5. Если написать эти цифры над и под значком интеграла, получится определенный интеграл.
Собственно и все, интеграл — это сумма бесконечно малых приращений (то есть значений) какой-то функции. Не сложно и не страшно, если не усложнять.
Что мы делаем? Разрезаем фигуру на «ленточки» изменяем площадь этих ленточек и собираем все обратно (суммируем).
Интересно, везде идет речь о сумме, а площадь считается умножением. Парадокс? Нет, умножение это ведь то же самое, что и сложение: 2+2+2+2=2*4. То же самое происходит и с площадью. Чтобы выяснить какова площадь прямоугольника со сторонами 5 и 4, перемножаем 5 на 4, или разделяем прямоугольник на 5 полосок шириной в «единицу» и складываем 4+4+4+4+4=5*4=20.
Никакого противоречия здесь нет. Вот только умножение работает в случае одинаковых величин, простых фигур или прямолинейного движения без ускорения. В остальных случаях — интегрирование.
Зачем нужен интеграл
Из примера выше уже понято, что одна из полезных задач интегрирования — это расчет площади криволинейных фигур. В любой сложной ситуации, если сложность эта заключается криволинейности или неравномерности мы используем интеграл.
Но лучший способ объяснить, что такое интеграл простыми словами — показать еще пару примеров. Как когда-то в детстве объяснили сложение на яблоках. Для чего интеграл может понадобиться?
Предположим, нужно построить храм кому-то из древнегреческих богов, такой чтобы место в нем хватило всем, крыша была прямоугольной, а колоны круглыми, ведь так красивее (а еще прочнее).
Давление колонны на фундамент легко посчитать, если она квадратного сечения, делим силу на площадь и вуаля. А если колонна круглого сечения? Какова площадь круга?
Можно конечно, не напрягаться, и заменить круг эквивалентным квадратом (квадратура круга), но каким? На всякий случай побольше, чтобы наверняка ничего не развалилось. Но это не наш метод, особенно, если ни бесконечного числа рабочих, ни бесконечного числа мрамора в действительности нет и взять негде, а казнить за неэффективное использование бюджета никто не запрещает.
Прием с эквивалентом площади на самом деле простой, использовался древними людьми. Очень-очень древние греки ничего не знали об интегрировании, а Архимед еще не родился, тем не менее, чтобы рассчитать площадь круга, в него выкладывались камешки. Когда круг заполнялся, камешки собирались и раскладывались в виде квадрата. Чем меньше камешки тем… Ничего не напоминает?
Еще примеры из жизни
Конечно, в физике интеграл «берут» постоянно. Вместо Х, может быть время, и тогда мы будем иметь дело с функцией времени, такой, например, как скорость. Ускорение — это скорость изменения скорости. Скорость, это скорость изменения координат. Пробежавшись от ускорения к скорости мы уже дважды использовали интеграл.
В обратную сторону: первая производная пути, это скорость, вторая производная — ускорение. Если ускорение равно нулю, значит скорость не менялась.
Интегрирование и дифференцирование, такие же «парочка» как и умножение и деление, суммирование и вычитание, только не с цифрами, а с функциями. Это взаимно-обратные операции. В случае производной, мы не «складываем», а «отнимаем».
Если проинтегрировав функцию изменения скорости (ускорение) получим константу (число, например, 60, а не формулу y=2x), значит, скорость не изменялась со временем, ускорения не было. Если, взяв приводную (дифференциал) функции скорости по времени, получим ноль — скорость не менялась, ускорение равно нулю.
То есть, имея в своем распоряжении какую-то функцию (зависимость чего-то от чего-то), мы можем ее дифференцировать или интегрировать. Точно также как если бы умножали и или, вычитали и складывали обычные числа.
Например, у нас есть функция изменения координат от времени. В реальном мире мы вышли на пробежку. Бежал наш виртуальный спортсмен 30 минут, первые 10 минут очень быстро, вторые 10 минут уже с одышкой, ну а последние 10 прошел пешком.
Очевидно, что координаты бегуна в начале и в конце разные (он же не стоял на месте). Если координаты менялись — скорость не равнялась нулю.
Скорость не была одинаковой, а менялась в зависимости от времени (больше времени, больше усталость, меньше скорость).
Итак, у нас есть функция изменения координат. Первая производная даст нам новую функцию — изменения координат, вторая производная — функцию ускорения. И первая и вторая функции зависят от одной и той же переменной — времени.
Еще один пример, вычисление массы. Масса, это произведение плотности на объем. Если плотность и объем одинаковы (это стакан воды) никаких проблем нет. А если плотность меняется (тот же стакан, только с коктейлем в несколько слоев)? В таком случае нужно знать закон (зависимость с которой изменяться плотность жидкости в стакане).
Если вам такие примеры не близки, то представьте себе, что взяли кредит под сложный процент. Тогда ваш долг будет расти не линейно. И вы будете интегрировать…
Если нужно узнать какую работу нужно затратить на перемещение предмета не по прямой, а если, нужно рассчитать лучшую цену, зная зависимость спроса от предложения, а если нужно посчитать за какое время рабочие выкопают яму, если это не роботы, а живые люди, которые устают со временем, а если…
Если посмотреть вокруг, не найдется в реальном мире ни идеальных фигур, ни ровных графиков, ни равномерного движения без ускорения, ни линейных зависимостей в поведении человека «разумного».
Все эти простые штуки из науки, просто частные случаи. А значит, в реальном мире интеграл более полезен, чем кажется. Конечно, кривые сложнее прямых и именно поэтому всю свою историю люди упрощали себе жизнь: делили поле прямыми, на квадраты и прямоугольники при помощи натянутой веревки. Считали среднюю скорость, а не мгновенную в каждой точке маршрута, полагали, что тело прошенное под углом к горизонту летит по параболе, а не баллистической кривой… Но, просто — не значит точно.
Говоря простым языком, интегрирование — это такой же инструмент, как и суммирование, в нем нет никаких особых тайн и сложностей. Кроме одной — представить себе бесконечность сложнее, чем натуральные числа, у которых есть наглядные представления в природе. Но справляемся же мы как-то с представлениями таких абстракций как «ноль» или «отрицательное число». С матанализом просто нужно чуть больше воображения.
Ну а если уж совсем просто, для гуманитариев, то производная винограда — это вино. Интеграл вина — это виноград.
Интегралы для чайников: как решать, правила вычисления, объяснение
Решение интегралов – задача легкая, но только для избранных. Эта статья для тех, кто хочет научиться понимать интегралы, но не знает о них ничего или почти ничего. Интеграл. Зачем он нужен? Как его вычислять? Что такое определенный и неопределенный интегралы?
Если единственное известное вам применение интеграла – доставать крючком в форме значка интеграла что-то полезное из труднодоступных мест, тогда добро пожаловать! Узнайте, как решать простейшие и другие интегралы и почему без этого никак нельзя обойтись в математике.
Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.
Изучаем понятие « интеграл »
Интегрирование было известно еще в Древнем Египте. Конечно, не в современном виде, но все же. С тех пор математики написали очень много книг по этой теме. Особенно отличились Ньютон и Лейбниц, но суть вещей не изменилась.
Как понять интегралы с нуля? Никак! Для понимания этой темы все равно понадобятся базовые знания основ математического анализа. Сведения о пределах и производных, необходимые и для понимания интегралов, уже есть у нас в блоге.
Неопределенный интеграл
Пусть у нас есть какая-то функция f(x).
Неопределенным интегралом функции f(x) называется такая функция F(x), производная которой равна функции f(x).
Другими словами интеграл – это производная наоборот или первообразная. Кстати, о том, как вычислять производные, читайте в нашей статье.
Первообразная существует для всех непрерывных функций. Также к первообразной часто прибавляют знак константы, так как производные функций, различающихся на константу, совпадают. Процесс нахождения интеграла называется интегрированием.
Простой пример:
Чтобы постоянно не высчитывать первообразные элементарных функций, их удобно свести в таблицу и пользоваться уже готовыми значениями.
Полная таблица интегралов для студентов
Определенный интеграл
Имея дело с понятием интеграла, мы имеем дело с бесконечно малыми величинами. Интеграл поможет вычислить площадь фигуры, массу неоднородного тела, пройденный при неравномерном движении путь и многое другое. Следует помнить, что интеграл – это сумма бесконечно большого количества бесконечно малых слагаемых.
В качестве примера представим себе график какой-нибудь функции.
Как найти площадь фигуры, ограниченной графиком функции? С помощью интеграла! Разобьем криволинейную трапецию, ограниченную осями координат и графиком функции, на бесконечно малые отрезки. Таким образом фигура окажется разделена на тонкие столбики. Сумма площадей столбиков и будет составлять площадь трапеции. Но помните, что такое вычисление даст примерный результат. Однако чем меньше и уже будут отрезки, тем точнее будет вычисление. Если мы уменьшим их до такой степени, что длина будет стремиться к нулю, то сумма площадей отрезков будет стремиться к площади фигуры. Это и есть определенный интеграл, который записывается так:

Точки а и b называются пределами интегрирования.

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Правила вычисления интегралов для чайников
Свойства неопределенного интеграла
Как решить неопределенный интеграл? Здесь мы рассмотрим свойства неопределенного интеграла, которые пригодятся при решении примеров.
Свойства определенного интеграла
Как считать определенный интеграл? С помощью формулы Ньютона-Лейбница.
Мы уже выяснили, что определенный интеграл – это предел суммы. Но как получить конкретное значение при решении примера? Для этого существует формула Ньютона-Лейбница:
Примеры решения интегралов
Ниже рассмотрим неопределенный интеграл и примеры с решением. Предлагаем самостоятельно разобраться в тонкостях решения, а если что-то непонятно, задавайте вопросы в комментариях.
Для закрепления материала посмотрите видео о том, как решаются интегралы на практике. Не отчаиваетесь, если интеграл не дается сразу. Обратитесь в профессиональный сервис для студентов, и любой тройной или криволинейный интеграл по замкнутой поверхности станет вам по силам.
Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.
Интегралы – что это, как решать, примеры решений и объяснение для чайников
За 4 минуты вы узнаете, что такое интегрирование. Как интеграл связан с производными. Чем отличается определенный интеграл от неопределенного. 5 примеров вычисления интегралов
Почему вы не знаете, как решать интегралы
А для чего нужны интегралы? Попробуйте сами себе ответить на этот вопрос.
Объясняя тему интегралов, учителя перечисляют малополезные школьным умам области применения. Среди них:
Связать все эти процессы не всегда получается, поэтому многие ученики путаются, даже при наличии всех базовых знаний для понимания интеграла.
Главная причина незнания – отсутствие понимания практической значимости интегралов.
Нужна помощь в написании работы?
Написание учебной работы за 1 день от 100 рублей. Посмотрите отзывы наших клиентов и узнайте стоимость вашей работы.
Интеграл – что это?
Предпосылки. Потребность в интегрировании возникла в Древней Греции. В то время Архимед начал применять для нахождения площади окружности методы, похожие по сути на современные интегральные исчисления. Основным подходом для определения площади неровных фигур тогда был «Метод исчерпывания», который достаточно лёгок для понимания.
Суть метода. В данную фигуру вписывается монотонная последовательность других фигур, а затем вычисляется предел последовательности их площадей. Этот предел и принимался за площадь данной фигуры.
Метод исчерпывания для определения площади круга
В этом методе легко прослеживается идея интегрального исчисления, которая заключается в нахождении предела бесконечной суммы. В дальнейшем эта идея применялась учёными для решения прикладных задач астронавтики, экономики, механики и др.
Современный интеграл. Классическая теория интегрирования была сформулирована в общем виде Ньютоном и Лейбницем. Она опиралась на существовавшие тогда законы дифференциального исчисления. Для её понимания, необходимо иметь некоторые базовые знания, которые помогут математическим языком описать визуальные и интуитивные представления об интегралах.
Объясняем понятие «Интеграл»
Процесс нахождения производной называется дифференцированием, а нахождение первообразной – интегрированием.
Интеграл математическим языком – это первообразная функции (то, что было до производной) + константа «C».
Интеграл простыми словами – это площадь криволинейной фигуры. Неопределенный интеграл – вся площадь. Определенный интеграл – площадь в заданном участке.
Интеграл записывается так:
Каждая подынтегральная функция умножается на компонент «dx». Он показывает, по какой переменной осуществляется интегрирование. «dx» – это приращение аргумента. Вместо X может быть любой другой аргумент, например t (время).
Неопределённый интеграл
Неопределенный интеграл не имеет границ интегрирования.
Для решения неопределённых интегралов достаточно найти первообразную подынтегральной функции и прибавить к ней «C».
Определённый интеграл
В определенном интеграле на знаке интегрирования пишут ограничения «a» и «b». Они указаны на оси X в графике ниже.
Точки A и B на оси X – есть ограничение зоны определения интеграла
Для вычисления определенного интеграла необходимо найти первообразную, подставить в неё значения «a» и «b» и найти разность. В математике это называется формулой Ньютона-Лейбница:
Таблица интегралов для студентов (основные формулы)
Скачайте формулы интегралов, они вам еще пригодятся
Как вычислять интеграл правильно
Существует несколько простейших операций для преобразования интегралов. Вот основные из них:
Вынесение константы из-под знака интеграла
Разложение интеграла суммы на сумму интегралов
Если поменять местами a и b, знак изменится
Можно разбить интеграл на промежутки следующим образом
Это простейшие свойства, на основе которых потом будут формулироваться более сложные теоремы и методы исчисления.
Примеры вычисления интегралов
Решение неопределенного интеграла
Решение определенного интеграла
Базовые понятия для понимания темы
Чтобы вы поняли суть интегрирования и не закрыли страницу от непонимания, мы объясним ряд базовых понятий. Что такое функция, производная, предел и первообразная.
Функция – правило, по которому все элементы из одного множества соотносятся со всеми элементами из другого.
Производная – функция, описывающая скорость изменения другой функции в каждой конкретной точке. Если говорить строгим языком, – это предел отношения приращения функции к приращению аргумента. Он вычисляется вручную, но проще использовать таблицу производных, в которой собрано большинство стандартных функций.
Приращение – количественное изменение функции при некотором изменении аргумента.
Предел – величина, к которой стремиться значение функции, при стремлении аргумента к определённому значению.
Пример предела: допустим при X равном 1, Y будет равно 2. Но что, если X не равен 1, а стремится к 1, то есть никогда её не достигает? В этом случае y никогда не достигнет 2, а будет только стремиться к этой величине. На математическом языке это записывается так: limY(X), при X –> 1 = 2. Читается: предел функции Y(X), при x стремящемся к 1, равен 2.
Как уже было сказано, производная – это функция, описывающая другую функцию. Изначальная функция может быть производной для какой-либо другой функции. Эта другая функция называется первообразной.
Заключение
Найти интегралы не трудно. Если вы не поняли, как это делать, прочитайте статью еще раз. Со второго раза становится понятнее. Запомните! Решение интегралов сводится к простым преобразованиям подынтегральной функции и поиска её в таблице интегралов.
Если текстовое объяснение вам не заходит, посмотрите видео о смысле интеграла и производной: