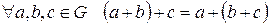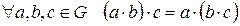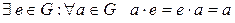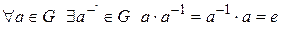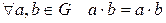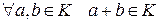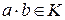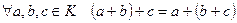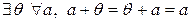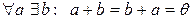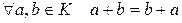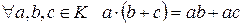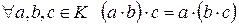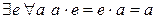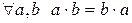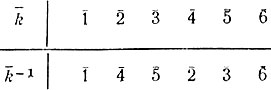Что такое группа кольцо поле

Группы, кольца, поля

Группой наз. множество G, для которого выполнены следующие аксиомы:

1) ассоциативность по сложению или умножению:

2) существование нейтрального элемента:

3) существование обратного элемента:

Группа наз. коммутативной, если

Кольцом наз. множество К на котором заданы две бинарные алгебраические операции сложения и умножения, и выполнены аксиомы:

0)

1) ассоциативность по сложению:

2) существование нейтрального элемента:

3) существование противоположного элемента:

Эти аксиомы являются обязательными. Если выполняются аксиомы:

6) ассоциативность по умножению, то кольцо наз. ассоциативным.

7) существование нейтрального элемента по умножению, то кольцо наз. кольцом с единицей.

8) коммутативность по умножению, то кольцо наз. коммутативным.

9) ,

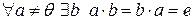
то говорят, что в этом кольце все не нулевые элементы обратимы.

Источник

Алгебраические структуры: группы, кольца, поля

Непустое множество (чаще всего чисел) называется алгебраической структурой, если на нём определены какие-либо операции, которые обладают определёнными свойствами. В математике чаще всего рассматриваются такие алгебраические структуры, как группы, поля и кольца. Если понятие алгебраической структуры или вообще множества для вас совсем новое, лучше будет изучить уроки Множества и операции над множествами и Множества чисел.

Алгебраические структуры: группы

Группой называется конечное или бесконечное множество (чаще всего чисел), на котором:

1) определена операция (например, умножение), которую можно выполнить, не выходя за пределы группы;

2) для элементов множества выполняется сочетальный (ассоциативный) закон (для любых a, b, c верно равенство (ab)c = a(bc) ).

3) существует так называемый единичный элемент e;

4) для каждого элемента a из этого множества существует обратный элемент такой, что , при этом единственный.

Если в группе выполняется переместительный (коммутативный) закон (для любых a и b верно равенство ab = ba ), то такую группу называют коммутативной или абелевой группой.

Алгебраические структуры: кольца

У множеств комплексных чисел, действительных чисел, рациональных чисел и целых чисел есть общая особенность: в них можно выполнять операции сложения, умножения и вычитания, оставаясь в границах множества.

Каждое множество чисел, которое содержит сумму, произведение и разность любых двух своих чисел, называется кольцом.

Алгебраические структуры: поля

Числовое кольцо называется числовым полем, если оно содержит частное любых двух своих чисел (делитель предполагается отличным от нуля). Следовательно, можно говорить о поле рациональных чисел, поле действительных чисел, поле комплексных чисел, в то время как кольцо целых чисел полем не является.

Поле можно определить и следующим образом. Множество называют полем, если в этом множестве по меньшей мере два элемента и для них

1) определена операция сложения;

1′) определена операция умножения;

2) для сложения выполняется сочетательный (ассоциативный) закон;

2′) для умножения выполняется сочетательный (ассоциативный) закон;

3) для сложения выполнятся переместительный (коммутативный) закон;

3′) для умножения выполняется переместительный (коммутативный) закон;

4) выполнима операция вычитания;

4′) выполнима операция деления, кроме деления на нуль.

Алгебраические структуры часто называют просто «алгебрами». Их используют в абстрактном моделировании. В частности, они могут быть применены в программировании. Например, когда нужно определить свойства и правила какой-либо структуры и установить запрет на добавление в эту структуру элемента, которое (добавление) нарушило бы свойства и правила для этой структуры.

Источник

Группы, кольца, поля в математике

Группа: определение и примеры групп

Множество с алгебраической операцией называется группой, если выполняются следующие условия:

1) операция в ассоциативна: ;

2) в существует нейтральный элемент ;

Решение. Действительно, операция умножения определена на указанном множестве, так как

Кольцо

1) относительно операции сложения множество — коммутативная группа, т.е.

а) операция сложения коммутативна: ;

б) операция сложения ассоциативна: ;

в) существует нулевой элемент ;

г) для каждого элемента существует противоположный ему элемент ;

2) операция умножения в множестве ассоциативна:

3) операции сложения и умножения связаны законами дистрибутивности:

Кольцами являются множества целых, рациональных, действительных чисел, причем все они — коммутативные кольца с единицей. Примеры других колец, в том числе и некоммутативных, встретятся в дальнейшем. Как видим, кольцо — это множество, в котором определены три операции: сложение, умножение и вычитание.

Если операция коммутативна, то дистрибутивность слева операции относительно операции влечет дистрибутивность справа, так как

Решение. В самом деле, для любых положительных действительных чисел справедливы равенства

Следовательно, операция дистрибутивна справа относительно операции умножения чисел. Дистрибутивность слева относительно умножения опровергается примером

Пример В.7. Доказать, что множество чисел вида, где и — целые числа, является кольцом:

Решение. Действительно, операции сложения и умножения определены на рассматриваемом множестве, так как сумма и произведение двух чисел вида (В.2) имеют тоже самое представление:

Таким образом, рассматриваемое множество удовлетворяет всем условиям определения кольца.

Поле: определение и примеры полей

1) — коммутативное кольцо с единицей ;

Как видим, поле — это множество, в котором определены четыре операции: сложение, умножение, вычитание и деление. Полями, например, являются множества рациональных и действительных чисел.

Пример В.8. На множестве трех целых чисел определим две операции:

1) «сложение по модулю 3» — остаток от деления суммы на 3 (обозначим через );

2) «умножение по модулю 3» — остаток от деления произведения на 3 (обозначим через ).

Доказать, что множество является полем относительно введенных операций.

– остаток от деления на 3 суммы не изменится, если слагаемое (или не сколько слагаемых) заменить его остатком при делении на 3:

– остаток от деления на 3 произведения не изменится, если множитель (или несколько множителей) заменить его остатком при делении на 3:

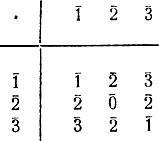
Рассматриваемые в примере операции «сложения по модулю 3» и «умножения по модулю 3» можно представить в виде

Покажем, что множество является коммутативным кольцом с единицей. В самом деле, операция «сложения по модулю 3» коммутативна и ассоциативна. Это следует из коммутативности и ассоциативности сложения чисел. Действительно, из равенства следует, что

Коммутативность доказана. Заметим, впрочем, что коммутативность «сложения по модулю 3» видна непосредственно по таблице (см. рис.В.2): слагаемые и в таблице можно поменять местами, при этом таблица не изменится.

Из равенства следует, что

Ассоциативность «сложения по модулю 3» доказана.

Итак, множество относительно операции «сложения по модулю 3» является коммутативной группой.

Операция «умножение по модулю 3» ассоциативна и коммутативна, что следует из ассоциативности и коммутативности умножения целых чисел, а также свойств остатков:

Следовательно, операция «умножения по модулю 3» дистрибутивна слева относительно операции «сложения по модулю 3». Дистрибутивность справа можно не проверять, так как обе операции коммутативны.

Единичным элементом служит число 1 (что видно по таблице «умножения по модулю 3»). Следовательно, — коммутативное кольцо с единицей.

Пример В.9. Доказать, что множество чисел вида, где и — рациональные числа, является полем:

Решение. Действительно, операции сложения и умножения определены на рассматриваемом множестве, так как сумма и произведение двух чисел вида (В.З) имеют тоже самое представление:

Так как рассматриваемое множество является коммутативным кольцом с единицей и каждый элемент, отличный от нуля, имеет обратный, то оно является полем.

Источник

Кольца, тела, поля

Определение 2.5. Кольцом называют алгебру сигнатура которой состоит из двух бинарных и двух нульарных операций, причем для любых выполняются равенства:

Операцию называют сложением кольца, операцию умножением кольца, элемент — нулем кольца, элемент — единицей кольца.

Равенства 1–7, указанные в определении, называют аксиомами кольца. Рассмотрим эти равенства с точки зрения понятия группы и моноида.

Связь между сложением кольца и умножением кольца устанавливает аксиома 7, согласно которой операция умножения дистрибутивна относительно операции сложения.

Замечание 2.2. В литературе встречается иной состав аксиом кольца, относящихся к умножению. Так, могут отсутствовать аксиома 6 (в кольце нет 1) и аксиома 5 (умножение не ассоциативно). В этом случае выделяют ассоциативные кольца (к аксиомам кольца добавляют требование ассоциативности умножения) и кольца с единицей. В последнем случае добавляются требования ассоциативности умножения и существования единицы.

Определение 2.6. Кольцо называют коммутативным, если его операция умножения коммутативна.

Пример 2.12. а. Алгебра есть коммутативное кольцо. Отметим, что алгебра кольцом не будет, поскольку — коммутативный моноид, но не группа.

в. Алгебра — коммутативное кольцо, что следует из свойств пересечения и симметрической разности множеств.

г. Пример некоммутативного кольца дает множество всех квадратных матриц фиксированного порядка с операциями сложения и умножения матриц. Единицей этого кольца является единичная матрица, а нулем — нулевая.

д. Пусть — линейное пространство. Рассмотрим множество всех линейных операторов, действующих в этом пространстве.

Основные аксиомы и тождества кольца

Аксиомы кольца называют также основными тождествами кольца. Тождество кольца — это равенство, справедливость которого сохраняется при подстановке вместо фигурирующих в нем переменных любых элементов кольца. Основные тождества постулируются, и из них затем могут быть выведены как следствия другие тождества. Рассмотрим некоторые из них.

Напомним, что аддитивная группа кольца коммутативна и в ней определена операция вычитания.

Теорема 2.8. В любом кольце выполняются следующие тождества:

Докажем третью пару тождеств. Рассмотрим первое из них. С учетом доказанного выше имеем

т.е. тождество справедливо. Второе тождество этой пары доказывается аналогично.

Первые два тождества из доказанных в теореме 2.8 выражают свойство, называемое аннулирующим свойством нуля в кольце. Третья же пара тождеств указанной теоремы выражает свойство дистрибутивности операции умножения кольца относительно операции вычитания. Таким образом, производя вычисления в любом кольце, можно раскрывать скобки и менять знаки так же, как и при сложении, вычитании и умножении действительных чисел.

Кольца и делители нуля

При отличных от нуля и приведенные матрицы являются делителями нуля.

Если в кольце имеются делители нуля, то подмножество всех ненулевых элементов кольца не образует группы по умножению уже хотя бы потому, что это подмножество не замкнуто относительно операции умножения, т.е. существуют ненулевые элементы, произведение которых равно нулю.

Кольцо, в котором множество всех ненулевых элементов по умножению образует группу, называют телом, коммутативное тело — полем, а группу ненулевых элементов тела (поля) по умножению — мультипликативной группой этого тела (поля). Согласно определению, поле есть частный случай кольца, в котором операции обладают дополнительными свойствами. Выпишем все свойства, выполнение которых требуется для операций поля. Их еще называют аксиомами поля.

б. Алгебры и есть поля, называемые полями действительных и комплексных чисел соответственно.

в. Примером тела, не являющегося полем, может служить алгебра кватернион.

Итак, мы видим, что известным законам сложения и умножения чисел соответствуют аксиомы поля. Занимаясь числовыми расчетами, мы «работаем в полях», а именно имеем дело преимущественно с полями рациональных и вещественных чисел, иногда «переселяемся» в поле комплексных чисел.

Источник

Что такое группа кольцо поле

3. Кольца и поля

Кольцом называется (непустое) множество K, на котором определены две операции (сложение и умножение), обладающие следующими свойствами:

1) множество K относительно сложения образует коммутативную группу;

2) умножение ассоциативно: для любых а, b, с ∈ K

3) сложение и умножение подчиняются дистрибутивному закону:

для любых а, b, с ∈ K.

При этом множество K, рассматриваемое лишь относительно операции сложения, называется аддитивной группой кольца.

Приведем некоторые примеры колец.

Читателю предлагается проверить выполнимость аксиом кольца в каждом из примеров. Остановимся подробнее на примере 3.

Поскольку операции над классами вычетов сводятся к операциям над числами из этих классов, то свойства ассоциативности и коммутативности этих операций вытекают из аналогичных свойств числового сложения и умножения. То же замечание относится к свойству дистрибутивности. Роль нулевого элемента при сложении играет класс 0‾. Противоположным элементом для класса вычетов r‾ ≠ 0‾ является класс n-r‾. Из определения сложения классов следует, что

В общем определении кольца не содержится требование коммутативности умножения. В том случае, если умножение обладает этим дополнительным свойством, кольцо называется коммутативным. В примерах 1-3 мы имеем как раз коммутативные кольца, а позднее (в приложении 5) познакомимся с важным примером некоммутативного кольца.

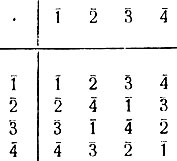
Рассмотрим таблицы умножения ненулевых элементов в кольцах вычетов Z₄ и Z₅.

Таблица 19

Таблица 20

Таблица 19 показывает, что в кольце могут существовать ненулевые элементы, произведение которых равно нулю: в Z₄ 2‾ · 2‾ = 0‾. Из этой же таблицы видно, что класс 2‾ необратим. Вообще, можно доказать, что ненулевые элементы, произведение которых равно нулю (называемые делителями нуля), всегда необратимы. С другой стороны, таблица 20 показывает, что в кольце Z₅ всякий ненулевой элемент обратим. Кольца с этим свойством имеют особое значение. Примем такое определение.

Коммутативное кольцо с единицей, в котором всякий ненулевой элемент обратим, называется полем.

Множество ненулевых элементов поля относительно умножения образует в силу определения поля коммутативную группу, которая называется мультипликативной группой поля.

Простейшими примерами числовых полей являются поле рациональных чисел Q и поле действительных чисел R (разумеется, относительно операций сложения и умножения чисел). Полем, как ясно из предыдущего, является и кольцо Z₅. Вообще, можно доказать, что при любом простом р (и только в этом случае) кольцо вычетов Z_p является полем. Оно называется полем вычетов по модулю р. В таблице 21 указаны элементы, обратные к ненулевым элементам поля вычетов Z₇.

Таблица 21

Конечные поля часто называют полями Галуа (их обозначают GF(g)); важное их свойство, используемое, в частности, и в теории кодирования, состоит в следующем:

Мультипликативная группа поля Галуа является циклической группой порядка q-1.

Образующий элемент мультипликативной группы поля Галуа называют примитивным элементом. Так, в поле Z₇ примитивным элементом является класс вычетов 3‾. Действительно, его степени

исчерпывают все ненулевые элементы поля.

Заметим, что класс 2 не является примитивным элементом в Z₇, так как среди его степеней нет, например, класса В. В то же время имеется очень много простых чисел р, для которых элемент ‾2 примитивен в Z_р. Так обстоит дело в полях Z₃, Z₅, Z₁₁ и т. д. В теории чисел известна следующая до сих пор не решенная задача:

Бесконечно ли множество тех простых чисел р, для которых ‾2 является примитивным элементом в Z_p?

Интересно, что с ответом на этот вопрос связано решение некоторых проблем теории кодирования.

Подмножество I кольца K называется его (двусторонним) идеалом, если оно само является кольцом относительно операций на K и если для любых элементов а ∈ K и b ∈ I оба произведения аb и bа принадлежат I.

Так, множество четных чисел есть идеал кольца Z. Читатель легко проверит, что и вообще всякое множество чисел, кратных какому-нибудь числу k, является идеалом кольца Z.

Рекомендуем читателю найти идеалы колец вычетов Z₅, Z₆, Z₈ и кольца многочленов R[X].

Источник