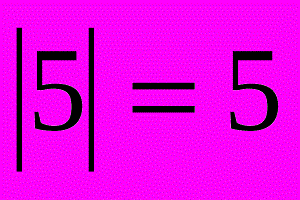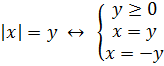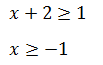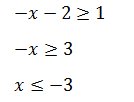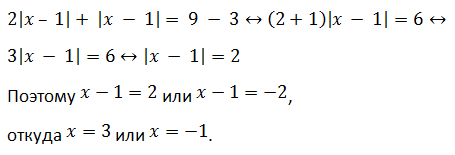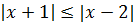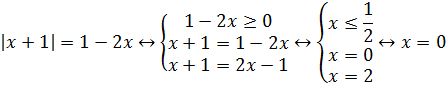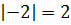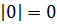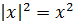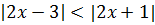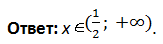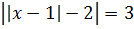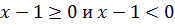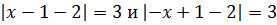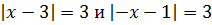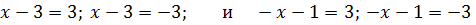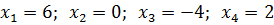Что такое двойной модуль
ДВОЙНОЙ МОДУЛЬ
— 1) То же, что бимодуль.2) Пара подгрупп Ни Fгруппы G, участвующая в разложении группы Gна двойные смежные классы, т. е. в разбиении G на непересекающиеся подмножеетва вида HxF, где х- элемент из G. Подмножество HxF наз. смежным классом группы Gпо Д. м. ( Н, F), или двойным смежным классом группы G ло модулю ( Н, F). Напр., разложение группы порядка 24 на двойные смежные классы по модулю ( Н, F), где Ни F- ее силовские 2- и 3-подгруппы, состоит из одного смежного класса по Д. м. ( Н, F). Любой двойной смежный класс HxF состоит из 

Лит.:[1] Холл М., Теория групп, пер. с англ., М., 1962.
Смотреть что такое «ДВОЙНОЙ МОДУЛЬ» в других словарях:
Двойной интеграл — В математическом анализе кратным или многократным интегралом называют множество интегралов взятых от переменных. Например: Замечание: кратный интеграл − это определенный интеграл, при его вычислении всегда получается число. Содержание 1… … Википедия
Число двойной точности — (Double precision, Double) компьютерный формат представления чисел, занимающий в памяти две последовательных ячейки (компьютерных слова; в случае 32 битного компьютера 64 бита или 8 байт). Как правило, обозначает формат числа с плавающей запятой… … Википедия
Мобильный модуль на шине PCI Express — (от англ. Mobile PCI Express Module (MXM)) стандарт взаимодействия для графических процессоров (Графические модули стандарта MXM) в лэптопах, в которых используется шина PCI Express, разработанная компанией Nvidia и несколькими производителями… … Википедия
БИМОДУЛЬ — двойной модуль, абелева группа В, являющаяся левым модулем над кольцом R и правым модулем над кольцом S, причем для любых В этом случае говорят, что имеет место ситуация или что Вявляется (R, S ) бимодулем. Б. Вможно рассматривать как левый… … Математическая энциклопедия
Спейсхэб — (англ. SPACEHAB) модуль, разработанный специально для полётов в американских многоразовых космических кораблях Спейс шаттл, который использовался в качестве грузового модуля или экспериментальной лаборатории в космосе на орбите Земли в … Википедия
Spacehab — Спейсхэб (англ. SPACEHAB) модуль, разработанный специально для кораблей спейс шаттл, который используется в качестве грузового модуля или экспериментальной лаборатории в космосе. Модуль «Спейсхэб» разработан в середине 80 х годов компанией с… … Википедия
STS-91 — Эмблема Полётные данные корабля … Википедия
Гори, Доминик Ли Падвилл — Доминик Ли Падвилл Гори Dominic Lee Pudwill Gorie Страна … Википедия
Дискавери STS-91 — п· Полётные данные корабля Название корабля Дискавери Стартовая площадка КЦ Кеннеди, СП 39 А[1] … Википедия
SGI Octane — SGI Octane2 (2000 2004) … Википедия
Неравенство с двумя модулями. Часть II
«Неравенство с двумя модулями. Часть I» смотрим здесь.
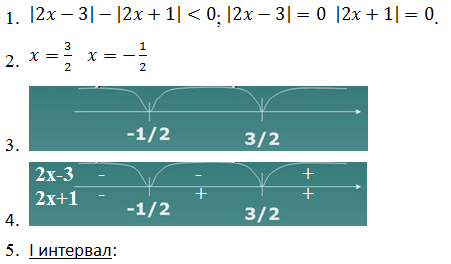
Решим неравенство
Правило раскрытия модуля говорит, что раскрытие модуля зависит от того, какой знак имеет подмодульное выражение. Стало быть, нас будут интересовать нули подмодульных выражений, – смена знака подмодульного выражения возможна только в них.
Вся числовая ось указанными точками разбивается на 4 промежутка. Нам предстоит поработать с неравенством в каждом из них.
Выясним, как распределяются знаки подмодульных выражений на каждом из промежутков.
Мы замечаем, что на двух промежутках (первом и третьем слева) знаки подмодульных выражений распределены одинаково.
Итак, первый случай:
Предстоит решить систему (мы объединили первый и третий промежутки в совокупность):
Во второй строке системы приводим подобные слагаемые и раскладываем на множители:
Теперь переходим на ось, пересекаем два множества между собой:
.
Второй случай:
.
Третий случай:
.
Нам осталось объединить решения каждого из случаев между собой:
Ответ:
Для тренировки предлагаю Вам решить следующее неравенство:
Модуль числа знак, свойства, действия, как найти, примеры графиков
Модуль числа легко найти, и теория, которая лежит в его основе, важна при решении задач.
Свойства и правила раскрытия, используемые при решении упражнений и на экзаменах, будут полезны школьникам и студентам.
Что такое модуль в математике
Модуль числа описывает расстояние на числовой линии от нуля до точки без учета того, в каком направлении от нуля лежит точка. Математическое обозначение: |x|.
Иными словами, это абсолютная величина числа. Определение доказывает, что значение никогда не бывает отрицательным.
Свойства модуля
Важно помнить о следующих свойствах:
Модуль комплексного числа
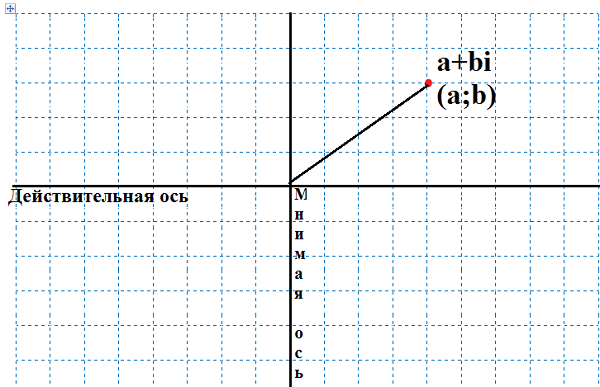
Абсолютной величиной комплексного числа называют длину направленного отрезка, проведенного от начала комплексной плоскости до точки (a, b).
Этот направленный отрезок также является вектором, представляющим комплексное число a + bi, поэтому абсолютная величина комплексного числа – это то же самое, что и величина (или длина) вектора, представляющего a+ bi.
Как решать уравнения с модулем
Уравнение с модулем – это равенство, которое содержит выражение абсолютного значения. Если для действительного числа оно представляет его расстояние от начала координат на числовой линии, то неравенства с модулем являются типом неравенств, которые состоят из абсолютных значений.
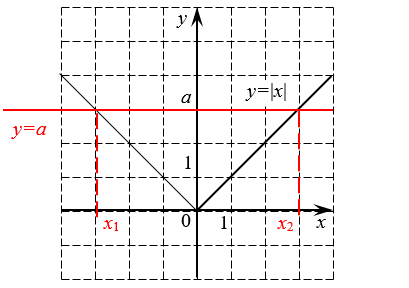
Уравнения типа |x| = a
Уравнение |x| = a имеет два ответа x = a и x = –a, потому что оба варианта находятся на координатной прямой на расстоянии a от 0.
Равенство с абсолютной величиной не имеет решения, если величина отрицательная.
Если |x| <, a представляет собой расстояние чисел от начала координат, это значит, что нужно искать все числа, чье расстояние от начала координат меньше a.
Уравнения типа |x| = |y|
Когда есть абсолютные значения по обе стороны уравнений, нужно рассмотреть обе возможности для приемлемых определений – положительные и отрицательные выражения.
Например, для равенства |x − a| = |x + b| есть два варианта: (x − a) = − (x + b) или (x − a) = (x + b).
Далее простая арифметика − нужно решить два равенства относительно x.
Уравнения типа |x| = y
Уравнения такого вида содержат абсолютную величину выражения с переменной слева от нуля, а справа – еще одну неизвестную. Переменная y может быть как больше, так и меньше нуля.
Для получения ответа в таком равенстве нужно решить систему из нескольких уравнений, в которой нужно убедиться, что y – неотрицательная величина:
Решение неравенств с модулем
Чтобы лучше понять, как раскрыть модуль в разных типах равенств и неравенств, нужно проанализировать примеры.
Уравнения вида |x| = a
Пример 1 (алгебра 6 класс). Решить: |x| + 2 = 4.
Решение.
Такие уравнения решаются так же, как и равенства без абсолютных значений. Это означает, что, перемещая неизвестные влево, а константы – вправо, выражение не меняется.
После перемещения константы вправо получено: |x| = 2.
Поскольку неизвестные связаны с абсолютным значением, это равенство имеет два ответа: 2 и −2.
Ответ: 2 и −2.
Пример 2 (алгебра 7 класс). Решить неравенство |x + 2| ≥ 1.
Решение.
Первое, что нужно сделать, это найти точки, где абсолютное значение изменится. Для этого выражение приравнивается к 0. Получено: x = –2.
Это означает, что –2 – поворотная точка.
Далее определяется знак на интервалах: на промежутке величина будет отрицательной, а на интервале будет положительной.
Разделим интервал на 2 части:
Общим ответом для этих двух неравенств является интервал [−1, + ∞).
Общим ответом для этих двух неравенств является интервал (−∞, –3].
Окончательное решение – объединение ответов отдельных частей:
Ответ: x ∈ (–∞, –3] ∪ [–1, + ∞).
Уравнения вида |x| = |y|
Пример 1 (алгебра 8 класс). Решить уравнение с двумя модулями: 2 * |x – 1| + 3 = 9 – |x – 1|.
Решение:
Ответ: x1 = 3, x2 = − 1.
Пример 2 (алгебра 8 класс). Решить неравенство:
Решение:
Уравнения вида |x| = y
Пример 1 (алгебра 10 класс). Найти x:
Решение:
Ответ: x = 0.
Модуль суммы
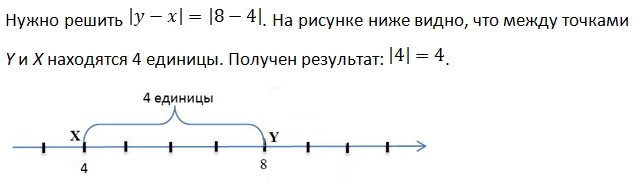
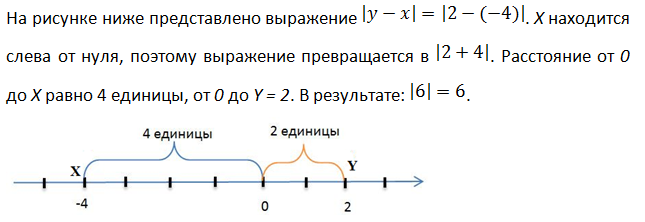
Модуль разности
Абсолютная величина разности двух чисел x и y равна расстоянию между точками с координатами X и Y на координатной прямой.
Пример 1.
Пример 2.
Модуль отрицательного числа
Для нахождения абсолютного значения числа, которое меньше нуля, нужно узнать, как далеко оно расположено от нуля. Поскольку расстояние всегда является положительным (невозможно пройти «отрицательные» шаги, это просто шаги в другом направлении), результат всегда положительный. То есть,
Проще говоря, абсолютная величина отрицательного числа имеет противоположное значение.
Модуль нуля
Вот почему нельзя сказать, что абсолютная величина – положительное число: ноль не является ни отрицательным, ни положительным.
Модуль в квадрате
Модуль в квадрате всегда равен выражению в квадрате:
Примеры графиков с модулем
Часто в тестах и на экзаменах встречаются задания, которые возможно решить, лишь проанализировав графики. Рассмотрим такие задания.
Пример 1.
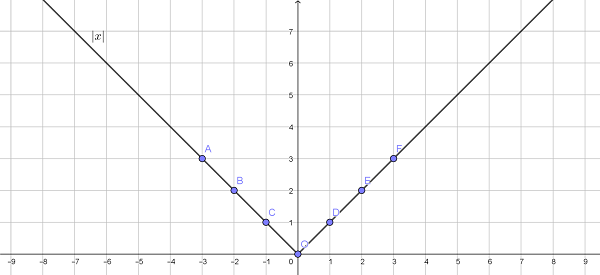
Дана функция f(x) = |x|. Необходимо построить график от – 3 до 3 с шагом 1.
Решение:
Объяснение: из рисунка видно, что график симметричен относительно оси Y.
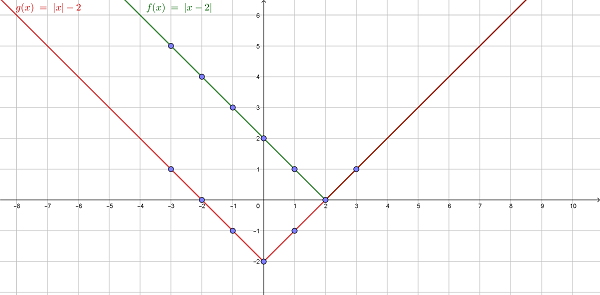
Пример 2. Необходимо нарисовать и сравнить графики функций f(x) = |x–2| и g(x) = |x|–2.
Решение:
Объяснение: константа внутри абсолютной величины перемещает весь график вправо, если ее значение отрицательное, и влево, если положительное. Но постоянная снаружи будет передвигать график вверх, если значение положительное, и вниз, если оно отрицательное (как –2 в функции g (x)).
Координата вершины x (точка, в которой соединяются две линии, вершина графа) – это число, на которое график сдвигается влево или вправо. А координата y – это значение, на которое график сдвигается вверх или вниз.
Строить такие графики можно с помощью онлайн приложений для построения. С их помощью можно наглядно посмотреть, как константы влияют на функции.
Метод интервалов в задачах с модулем
Метод интервалов – один из лучших способов найти ответ в задачах с модулем, особенно если в выражении их несколько.
Для использования метода нужно совершить следующие действия:
Пример 1. Решить методом интервалов.
Решение:
Результатом будет сумма всех подходящих интервалов.
Модуль в модуле
Среди примеров часто встречаются уравнения, где нужно найти корни равенств такого вида: ||ax – b| – c| = kx + m.
Лучше всего понять принцип на примере.
Пример 1. Решить
Решение:
Первым делом нужно раскрыть внутренний модуль. Для этого рассматривается два варианта:
В первом случае выражение положительное, а во втором отрицательное. Исходя из этого, получаем:
Нужно упростить два уравнения:
Далее каждое из равенств разделяется еще на два:
Получено четыре результата:
Заключение
Самое важное, что нужно знать: модуль не может быть отрицательным.
Поэтому, если представлено выражение, похожее на |2 – 4x| = –7 стоит помнить, что равенство неверно даже без поисков ответов.
В качестве итогов, напомним все свойства, которые помогут в решении задач:
Решать равенства и неравенства можно разными способами, но лучше всего использовать графический способ или метод интервалов.
Математическая энциклопедия
— 1) То же, что бимодуль.2) Пара подгрупп Ни Fгруппы G, участвующая в разложении группы Gна двойные смежные классы, т. е. в разбиении G на непересекающиеся подмножеетва вида HxF, где х- элемент из G. Подмножество HxF наз. смежным классом группы Gпо Д. м. ( Н, F), или двойным смежным классом группы G ло модулю ( Н, F). Напр., разложение группы порядка 24 на двойные смежные классы по модулю ( Н, F), где Ни F- ее силовские 2- и 3-подгруппы, состоит из одного смежного класса по Д. м. ( Н, F). Любой двойной смежный класс HxF состоит из смежных классов группы Gпо подгруппе Fи одновременно из смежных классов группы Gпо подгруппе Н, где |U:V| означает индекс подгруппы Vв группе U. Лит.:[1] Холл М., Теория групп, пер. с англ., М., 1962. В. Д. Мазуров.
Смотреть значение Двойной Модуль в других словарях
Двойной — удвоенный, сдвоенный, взятый или сделанный вдвое, вдвойне, дважды; передвоенный, сугубый, вдвое больший. труд, двойная и плата. Зубы двойные, а руки одинакие, о еде и работе.
Толковый словарь Даля
Двойной — двойная, двойное. 1. Вдвое больший, увеличенный в два раза. расход. Материя двойной ширины. Двойное жалование. 2. Состоящий из двух однородных частей, предметов. подбородок.
Толковый словарь Ушакова
Двойной Прил. — 1. Состоящий из двух одинаковых или подобных предметов, элементов, частей и т.п. // Осуществляемый в два приема, повторяющийся дважды. 2. Проявляющийся в двух видах; двоякий.
Толковый словарь Ефремовой
Аукцион Двойной — форма проведения торга, в котором конкурируют и продавцы, и покупатели, а цена устанавливается на уровне равновесия спроса и предложения, когда число продавцов по этой.
Экономический словарь
Аукцион Двойной — форма проведения
торга, в котором конкурируют и продавцы, и покупатели, а
цена устанавливается на уровне равновесия
спроса и
предложения, когда число.
Экономический словарь
Двойной Аукцион (double Auction) — – форма аукциона, в котором цены предлагают как покупатели, так и продавцы ценной бумаги. Проводится, если установленная биржевым «специалистом» разница цен покупки.
Экономический словарь
Двойной Валютный Курс — См. Курс валютный двойной
Экономический словарь
Двойной Выход — (Double Exit)
Использование двух паспортов для введения в
заблуждение или удобства.
Экономический словарь
Двойной Курс — метод государственного регулирования валютных операций, заключающийся в двойной котировке
курса национальной валюты: установлении разных курсов по финансовым.
Экономический словарь
Двойной Опцион — право
опциона либо купить, либо продать
контракт по базисной цене (но не купить и продать одновременно).
Экономический словарь
Двойной Орел — DOUBLE EAGLEЗолотая
монета США в 20 дол. весом 516 г и пробой 0,900.
Закон о
золотом
резерве, принятый 30 января 1934 г., приостановил чеканку ЗОЛОТЫХ МОНЕТ, и только.
Экономический словарь
Двойной Рейтинг — Ситуация, когда два основных рейтинговых агентства, таких, как Standard & Poors и Инвесторская служба Moodys, присваивают одним и тем же ценным бумагам различные рейтинги.
Экономический словарь
Двойной Таможенный Тариф — тариф, включающий два ряда ставок таможенных пошлин: минимальные для товаров стран, с которыми заключены специальные таможенные соглашения, и максимальные ставки для.
Экономический словарь
Двуствольный, Облигация С Двойной Гарантией — Муниципальная доходная облигация, основная сумма и проценты по которой гарантируются более крупным муниципальным ведомством. Например, орган, занимающийся эксплуатацией.
Экономический словарь
Контроль Двойной — англ. dual control действия требующие для их совершения одновременного согласия двух сторон, например, две подписи на документе, два ключа от банковского сейфа, арендуемого.
Экономический словарь
Курс Валютный Двойной — двойная котировка курса национальной валюты для коммерческих и финансовых операций.
Экономический словарь
Максимум Двойной — график изменения курса определенной ценной бумаги, согласно которому курс дважды поднимается до максимального уровня, что вызывает сопротивление повышению курса.
Экономический словарь
Минимум Двойной — график изменения курса ценных бумаг, согласно которому курс дважды опускается до своего минимального уровня и вновь поднимается. При анализе состояния рынка М.д. означает.
Экономический словарь
Опцион Двойной — CALL OF MOREТермин Лондонской фондовой
биржи, обозначающий
опцион, к-рый дает покупателю
право однократной покупки такого же количества акций по той же цене.
Экономический словарь
Орел Двойной — золотая монета в США достоинством в 20 долларов. Выпускается в тезаврационных целях.
Экономический словарь
Как решать уравнения с модулем: основные правила
Модуль — одна из тех вещей, о которых вроде-бы все слышали, но в действительности никто нормально не понимает. Поэтому сегодня будет большой урок, посвящённый решению уравнений с модулями.
Сразу скажу: урок будет несложный. И вообще модули — вообще тема относительно несложная. «Да конечно, несложная! У меня от неё мозг разрывается!» — скажут многие ученики, но все эти разрывы мозга происходят из-за того, что у большинства людей в голове не знания, а какая-то хрень. И цель этого урока — превратить хрень в знания.:)
Немного теории
Ещё один важный факт: модуль никогда не бывает отрицательным. Какое бы число мы ни взяли — хоть положительное, хоть отрицательное — его модуль всегда оказывается положительным (или в крайнем случае нулём). Именно поэтому модуль часто называют абсолютной величиной числа.
Кроме того, если объединить определение модуля для положительного и отрицательного числа, то получим глобальное определение модуля для всех чисел. А именно: модуль числа равен самому этому числу, если число положительное (или ноль), либо равен противоположному числу, если число отрицательное. Можно записать это в виде формулы:
Ещё есть модуль нуля, но он всегда равен нулю. Кроме того, ноль — единственное число, которое не имеет противоположного.
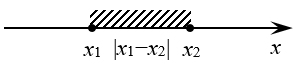
Из этого определения также следует, что модуль всегда неотрицателен. Но хватит определений и теории — перейдём к настоящим уравнениям.:)
Основная формула
Ну хорошо, с определением разобрались. Но легче-то от этого не стало. Как решать уравнения, содержащие этот самый модуль?
Спокойствие, только спокойствие. Начнём с самых простых вещей. Рассмотрим что-нибудь типа такого:
\[\left| f\left( x \right) \right|=a\]
Обратим внимание на второе уравнение. Про него сразу можно сказать: корней у него нет. Почему? Всё правильно: потому что в нём требуется, чтобы модуль был равен отрицательному числу, чего никогда не бывает, поскольку мы уже знаем, что модуль — число всегда положительное или в крайнем случае ноль.
\[\left| 2x+1 \right|=5\Rightarrow 2x+1=5\]
\[2x+1=5\Rightarrow 2x=4\Rightarrow x=2\]
Особо недоверчивые могут попробовать подставить найденный корень в исходное уравнение и убедиться, что действительно под модулем будет положительное число.
Теперь разберём случай отрицательного подмодульного выражения:
\[2x+1=-5\Rightarrow 2x=-6\Rightarrow x=-3\]
Да, такой алгоритм существует. И сейчас мы его разберём.
Избавление от знака модуля
\[\left| f\left( x \right) \right|=a\Rightarrow f\left( x \right)=\pm a\]
Таким образом, наше уравнение с модулем распадается на два, но уже без модуля. Вот и вся технология! Попробуем решить парочку уравнений. Начнём вот с такого
\[\left| 5x+4 \right|=10\Rightarrow 5x+4=\pm 10\]
Отдельно рассмотрим, когда справа стоит десятка с плюсом, и отдельно — когда с минусом. Имеем:
Ок, не вопрос, давайте рассмотрим что-нибудь чуть посерьёзнее:
Опять раскрываем модуль с плюсом и минусом:
Опять пара строчек — и ответ готов! Как я и говорил, в модулях нет ничего сложного. Нужно лишь запомнить несколько правил. Поэтому идём дальше и приступаем с действительно более сложным задачам.
Случай переменной правой части
А теперь рассмотрим вот такое уравнение:
Как быть в таком случае? Во-первых, надо раз и навсегда понять, что если правая часть уравнения окажется отрицательной, то уравнение не будет иметь корней — мы уже знаем, что модуль не может быть равен отрицательному числу.
А во-вторых, если права часть всё-таки положительна (или равна нулю), то можно действовать точно так же, как раньше: просто раскрыть модуль отдельно со знаком «плюс» и отдельно — со знаком «минус».
\[\left| f\left( x \right) \right|=g\left( x \right)\Rightarrow \left\< \begin
Применительно к нашему уравнению получим:
\[\left| 3x-2 \right|=2x\Rightarrow \left\< \begin
Поэтому решим-ка само уравнение:
Подозреваю, что кто-то из учеников уже начал скучать? Что ж, рассмотрим ещё более сложное уравнение:
Хоть оно и выглядит злобно, по факту это всё то же самое уравнение вида «модуль равен функции»:
\[\left| f\left( x \right) \right|=g\left( x \right)\]
И решается оно точно так же:
С неравенством мы потом разберёмся — оно какое-то уж слишком злобное (на самом деле простое, но мы его решать не будем). Пока лучше займёмся полученными уравнениями. Рассмотрим первый случай — это когда модуль раскрывается со знаком «плюс»:
Ну, тут и ежу понятно, что нужно всё собрать слева, привести подобные и посмотреть, что получится. А получится вот что:
Тут мы воспользовались важным свойством произведения, ради которого мы и раскладывали исходный многочлен на множители: произведение равно нулю, когда хотя бы один из множителей равен нулю.
Теперь точно так же разберёмся со вторым уравнением, которое получается при раскрытии модуля со знаком «минус»:
Опять то же самое: произведение равно нулю, когда равен нулю хотя бы один из множителей. Имеем:
Как видите, даже в этом случае ничего сложного не было — уравнения с модулями всегда решаются по алгоритму. Нужно лишь хорошо разбираться в многочленах и неравенствах. Поэтому переходим к более сложным задачам — там уже будет не один, а два модуля.
Уравнения с двумя модулями
Но детский сад закончился — пора рассмотреть что-нибудь посерьёзнее. Начнём с уравнений вот такого типа:
\[\left| f\left( x \right) \right|=\left| g\left( x \right) \right|\]
Это уравнение вида «модуль равен модулю». Принципиально важным моментом является отсутствие других слагаемых и множителей: только один модуль слева, ещё один модуль справа — и ничего более.
Кто-нибудь сейчас подумает, что такие уравнения решаются сложнее, чем то, что мы изучали до сих пор. А вот и нет: эти уравнения решаются даже проще. Вот формула:
\[\left| f\left( x \right) \right|=\left| g\left( x \right) \right|\Rightarrow f\left( x \right)=\pm g\left( x \right)\]
Всё! Мы просто приравниваем подмодульные выражения, ставя перед одним из них знак «плюс-минус». А затем решаем полученные два уравнения — и корни готовы! Никаких дополнительных ограничений, никаких неравенств и т.д. Всё очень просто.
Давайте попробуем решать вот такую задачу:
\[\left| 2x+3 \right|=\left| 2x-7 \right|\]
Элементарно, Ватсон! Раскрываем модули:
\[\left| 2x+3 \right|=\left| 2x-7 \right|\Rightarrow 2x+3=\pm \left( 2x-7 \right)\]
Рассмотрим отдельно каждый случай:
Со вторым уравнением всё чуть интереснее, но тоже очень и очень просто:
\[2x+3=-2x+7\Rightarrow 4x=4\Rightarrow x=1\]
Как видим, всё решилось буквально в пару строчек — другого от линейного уравнения мы и не ожидали.:)
Ну как? Сложно? Конечно, нет. Попробуем что-нибудь ещё:
Возможно, кто-то сейчас спросит: «Эй, что за бред? Почему «плюс-минус» стоит у правого выражения, а не у левого?» Спокойно, сейчас всё объясню. Действительно, по-хорошему мы должны были переписать наше уравнение следующим образом:
Затем нужно раскрыть скобки, перенести все слагаемые в одну сторону от знака равенства (поскольку уравнение, очевидно, в обоих случаях будет квадратным), ну и дальше отыскать корни. Но согласитесь: когда «плюс-минус» стоит перед тремя слагаемыми (особенно когда одно из этих слагаемых — квадратное выражение), это как-то более сложно выглядит, нежели ситуация, когда «плюс-минус» стоит лишь перед двумя слагаемыми.
Но ведь ничто не мешает нам переписать исходное уравнение следующим образом:
\[\left| x-1 \right|=\left| <
Что произошло? Да ничего особенного: просто поменяли левую и правую часть местами. Мелочь, которая в итоге немного упростит нам жизнь.:)
В общем, решаем это уравнение, рассматривая варианты с плюсом и с минусом:
Миссия выполнена! Можно взять с полки и скушать пирожок. Там их 2, ваш средний.:)
Важное замечание. Наличие одинаковых корней при разных вариантах раскрытия модуля означает, что исходные многочлены раскладываются на множители, и среди этих множителей обязательно будет общий. Действительно:
\[\left| x-1 \right|=\left| x-1 \right|\cdot \left| x-2 \right|\]
Как видим, у нас действительно возник общий множитель. Теперь, если собрать все модули с одной стороны, то можно вынести этот множитель за скобку:
Ну а теперь вспоминаем, что произведение равно нулю, когда хотя бы один из множителей равен нулю:
\[\left[ \begin
Таким образом, исходное уравнение с двумя модулями свелось к двум простейшим уравнениям, о которых мы говорили в самом начале урока. Такие уравнения решаются буквально в пару строчек.:)
Данное замечание, возможно, покажется излишне сложным и неприменимым на практике. Однако в реальности вам могут встретиться куда более сложные задачи, нежели те, что мы сегодня разбираем. В них модули могут комбинироваться с многочленами, арифметическими корнями, логарифмами и т.д. И в таких ситуациях возможность понизить общую степень уравнения путём вынесения чего-либо за скобку может оказаться очень и очень кстати.:)
Теперь хотелось бы разобрать ещё одно уравнение, которое на первый взгляд может показаться бредовым. На нём «залипают» многие ученики — даже те, которые считают, что хорошо разобрались в модулях.
Тем не менее, это уравнение решается даже проще, чем то, что мы рассматривали ранее. И если вы поймёте почему, то получите ещё один приём для быстрого решения уравнений с модулями.
В чём вообще проблема? А проблема в том, что каждый модуль — число положительное, либо в крайнем случае ноль. А что будет, если сложить два положительных числа? Очевидно, снова положительное число:
Последняя строчка может натолкнуть на мысль: единственный случай, когда сумма модулей равна нулю — это если каждый модуль будет равен нулю:
А когда модуль равен нулю? Только в одном случае — когда подмодульное выражение равно нулю:
\[x-<
\[<
Метод расщепления
Что ж, мы уже рассмотрели кучу задач и изучили множество приёмов. Думаете, на этом всё? А вот и нет! Сейчас мы рассмотрим заключительный приём — и одновременно самый важный. Речь пойдёт о расщеплении уравнений с модулем. О чём вообще пойдёт речь? Давайте вернёмся немного назад и рассмотрим какое-нибудь простое уравнение. Например, это:
Собственно, в этой неоднозначности и состоит вся проблема: поскольку число под модулем меняется (оно зависит от переменной), нам неясно — положительное оно или отрицательное.
\[3x-5 \gt 0\Rightarrow \left| 3x-5 \right|=3x-5\]
Таким образом, наше уравнение превратится в линейное, которое легко решается:
\[3x-5=5-3x\Rightarrow 6x=10\Rightarrow x=\frac<5><3>\]
\[x=\frac<5><3>\Rightarrow 3x-5=3\cdot \frac<5><3>-5=5-5=0\]
\[3x-5 \lt 0\Rightarrow \left| 3x-5 \right|=5-3x\]
Очевидно, что в модуль раскроется со знаком «минус». Но тогда возникает странная ситуация: и слева, и справа в исходном уравнении будет торчать одно и то же выражение:
\[3x-5 \lt 0\Rightarrow 3x \lt 5\Rightarrow x \lt \frac<5><3>\]
Другими словами, ответом будет не какое-то отдельное число, а целый интервал:
\[3x-5=0\Rightarrow \left| 3x-5 \right|=0\]
\[0=3x-5\Rightarrow 3x=5\Rightarrow x=\frac<5><3>\]
Таким образом, помимо интервала нас устроит ещё и число, лежащее на самом конце этого интервала:
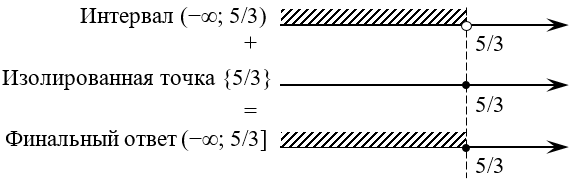
Куда важнее другое: мы только что разобрали универсальный алгоритм решения уравнения с модуляем! И состоит этот алгоритм из следующих шагов:

Ну и какие тут интервалы? Понятно, что их три:
Я думаю, вы уже поняли закономерность. Каждый интервал включает в себя левый конец и не включает правый.
На первый взгляд, такая запись может показаться неудобной, нелогичной и вообще какой-то бредовой. Но поверьте: после небольшой тренировки вы обнаружите, что именно такой подход наиболее надёжен и при этом не мешает однозначно раскрывать модули. Лучше уж использовать такую схему, чем каждый раз думать: отдавать левый/правый конец в текущий интервал или «перекидывать» его в следующий.
На этом урок заканчивается. Скачивайте задачи для самостоятельного решения, тренируйтесь, сравнивайте с ответами — и увидимся в следующем уроке, который будет посвящён неравенствам с модулями.:)