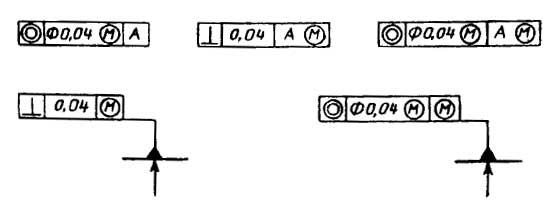
Что такое допуск биения в заданном направлении

Что такое допуск биения в заданном направлении

Суммарные отклонения и допуски формы и расположения

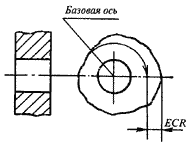
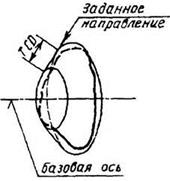
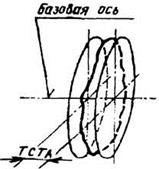
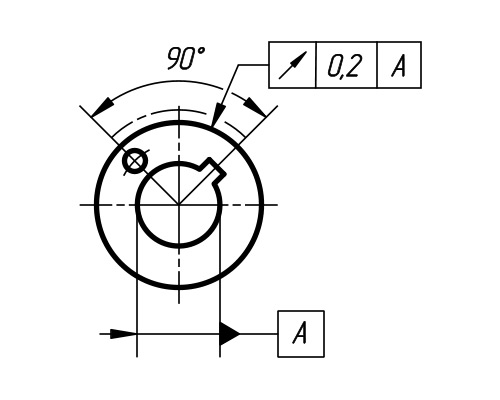
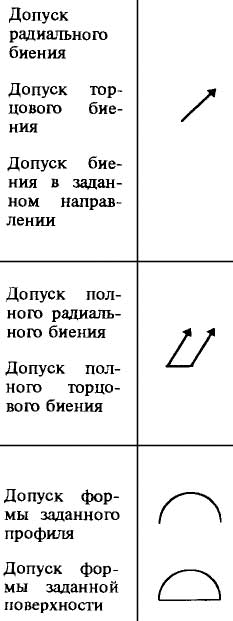
4.1. Радиальное биение ECR и допуск радиального биения TCR

вращения до базовой оси в сечении плоскостью, перпенди­кулярной базовой оси

концентричны­ми окружностями с центром, лежащим на базовой оси, и отстоящими друг от друга на расстоянии, равном

допуску радиального бие­ния TCR

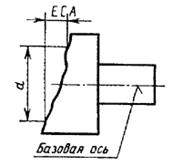
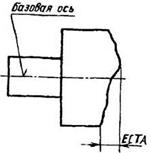
4.2. Торцовое биение ЕСА и допуск торцового биения ТСА

поверхности до плоскости, перпендикулярной базовой оси.

Примечание. Торцовое биение определяется в сечении торцовой поверхности цилиндром задан­ного диаметра, соосным

с базовой осью, а если диа­метр не задан, то в сечении любого (в том числе и наибольшего) диаметра торцовой поверхности

любому (в том числе и наибольшему) диаметру торцовой поверхности, а ось совпадает с базовой осью, ограниченная двумя

параллельными плоско­стями, отстоящими друг от друга на расстоя­нии, равном допуску торцового биения ТСА, и

перпендикулярными базовой оси

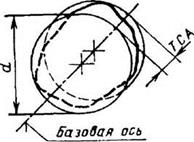
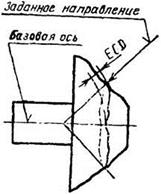
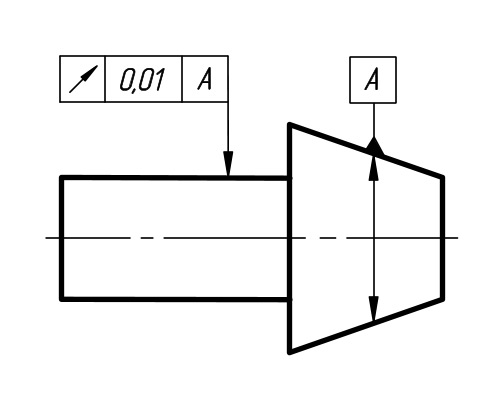
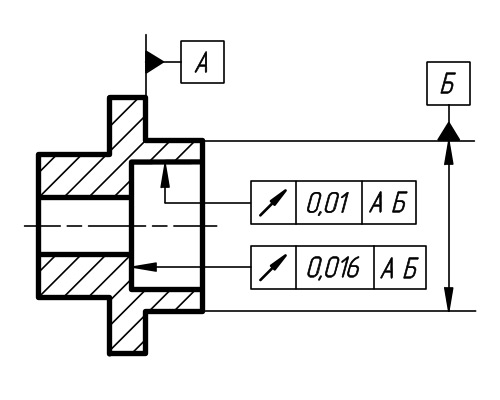
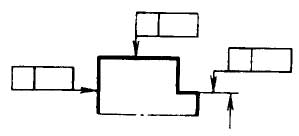
4.3. Биение ECD и допуск биения в заданном направлении TCD

поверх­ности вращения в сечении рассматриваемой поверхности конусом, ось которого совпадает с базовой осью,

а образующая имеет заданное направление, до вершины этого конуса.

(Направление рекомендуется задавать по норма­ли к рассматриваемой поверхности. Биение является результатом совместного

прояв­ления в заданном направлении отклонений формы профиля рассматриваемого сечения и отклонений расположения оси

рассматриваемой поверхности относительно базы)

базовой осью, а образующая имеет заданное направление, ограниченная двумя параллельными плоско­стями, отстоящими

друг от друга на расстоя­нии вдоль образующей конуса, равном допус­ку биения TCD, и перпендикулярными базо­вой оси

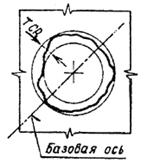
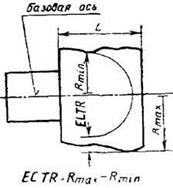
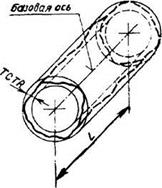
4.4. Полное радиальное биение ECTR и допуск полного радиального биения TCTR

(Термины в п. 4.4 относятся к поверхностям с номинальной цилиндрической формой)

в пределах нормируемого участка до базовой оси.

(Полное радиальное биение является результатом совместного проявления отклонения от цилиндричности рассматриваемой

поверхности и отклонения от ее соосности относительно базы)

совпадает с базовой осью, а боковые поверхности отстоят друг от друга на расстоянии, равном допуску полного радиального

4.5. Полное торцовое биение ЕСТА и допуск полного торцового биения ТСТА

(Термины в п. 4.5 относятся к торцовым поверхностям с номинальной плоской формой)

до плоскости, перпендикулярной базовой оси. (Полное торцовое биение является результатом со­вместного проявления

отклонения от плоскостности рассматриваемой поверхности и отклонения от ее перпендикулярности относительно базы)

отстоя­щими друг от друга на расстоянии, равном допуску полного торцового биения ТСТА и перпендикулярными базовой оси

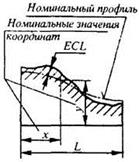
4.6. Отклонение ECL и допуск формы заданного профиля TCL

профиля, опреде­ляемое по нормали к номинальному профилю в пределах нормируемого участка

4.6.2. Допуск формы заданного профиля:

двумя линия­ми, эквидистантными номинальному профи­лю, и отстоящими друг о друга на расстоя­нии, равном допуску

формы заданного про­филя в диаметральном выражении TCL или удвоенному допуску формы заданного профи­ля в

радиусном выражении TCL/2. Линии, ограничивающие поле допуска, являются огибающими семейства окружно­стей,

диаметр которых равен допуску формы заданного профиля в диаметральном выраже­нии TCL, а центры находятся

на номиналь­ном профиле

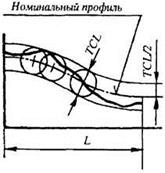
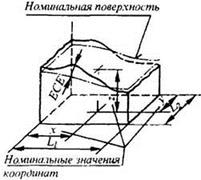
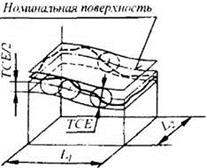
4.7. Отклонение ЕСЕ и допуск формы заданной поверхности ТСЕ

поверх­ности, определяемое по нормали к номиналь­ной поверхности в пределах нормируемого участка

4.7.2. Допуск формы заданной поверхности:

эквидистантными но­минальной поверхности и отстоящими друг от друга на расстоянии, равном допуску фор­мы

заданной поверхности в диаметральном выражении ТСЕ или удвоенному допуску формы заданной поверхности

в радиусном выражении ТСЕ/2.

Поверхности, ограничивающие поле до­пуска, являются огибающими семейства сфер, диаметр которых равен допуску формы

задан­ной поверхности в диаметральном выражении ТСЕ, а центры находятся на номинальной поверхности.

1. Термины в пл. 4.6 и 4.7 применяются в тех случаях, когда профиль (поверхность) задан номи­нальными размерами –

координатами отдельных точек профиля (поверхности) или размерами его элементов без предельных отклонении этих

размеров (размерами в рамках).

2. В тех случаях, когда базы не заданы, располо­жение номинального профиля (поверхности) относи­тельно реального

определяется условием получения минимального отклонения формы профиля (поверх­ности).

3. Отклонение формы заданного профиля (поверхности) является результатом совместного проявления отклонении

размеров и формы профиля (поверхности), а также отклонении расположения его относительно заданных баз.

4. Кроме тех видов суммарных отклонении и до­пусков, которые приведены в пл. 4.1 – 4.7, в обосно­ванных случаях могут

нормироваться и другие сум­марные отклонения формы и расположения поверх­ностей или профилей (см. ГОСТ 24642-81)

Источник

23. Точность формы деталей. Допуски, посадки и технические измерения.

23. Точность формы деталей. Допуски, посадки и технические измерения. 23. Точность формы деталей. Допуски, посадки и технические измерения.

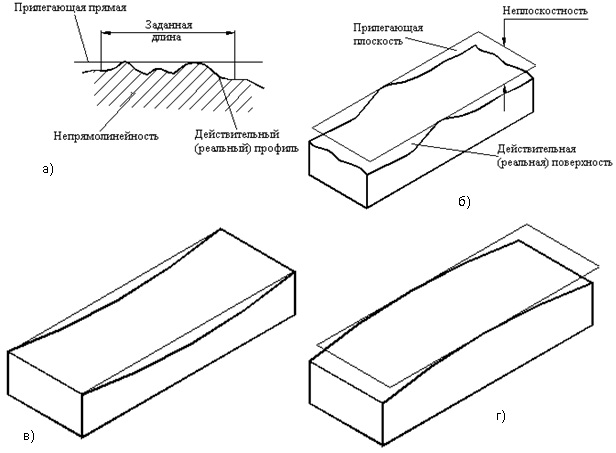
Под отклонением формы понимается совокупность отклонений формы действительной поверхности (или профиля) от формы номиналь¬ной поверхности (или профиля), заданной чертежом. За величину откло¬нения формы принимается наибольшее расстояние от точек действитель¬ной поверхности до прилегающей поверхности.

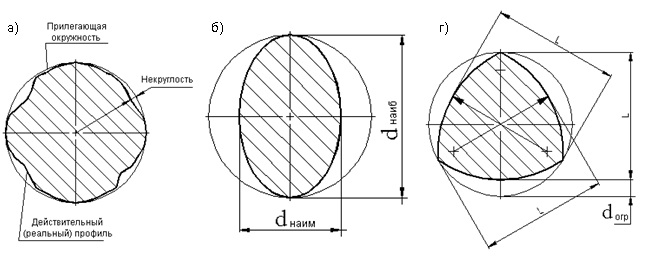
Точность формы цилиндрических поверхностей определяется точностью контура в поперечном (перпендикулярном оси) сечении и точностью образующих цилиндра в продольном (проходящем через ось) сечении. Контур поперечного сечения цилиндрического тела описывается окружностью. Показателем отклонений контура поперечного сечения является некруглость — отклонение от окружности (рис. 44, а).

При отсутствии огранки с нечетным числом граней некруглость определяется как полуразность между наибольшим и наименьшим диаметрами сечения, измеренными двухконтактным прибором.

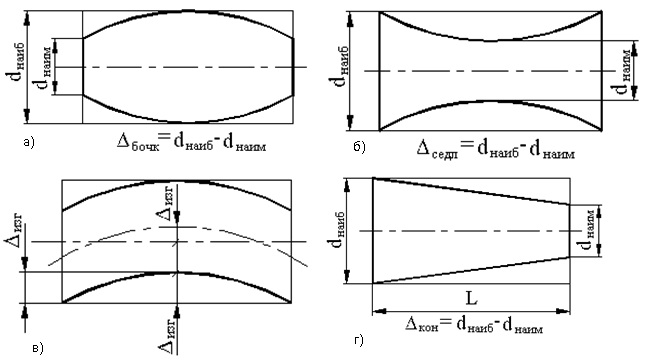
К дифференцированным отклонениям формы в поперечном сечении относятся овальность и огранка. Овальность (рис. 44, б) — отклонение от окружности, при котором дей-ствительный профиль представляет со¬бой овалообразную фигуру, наибольший и наимень-ший диаметры которой (вдоль большой и малой осей овала) находятся во взаимно перпенди-кулярных направлениях. За величину овальности принимается разность между наибольшим и наименьшим диаметрами сечения, т.е. удвоенная величина некруглости. Огранка (рис. 44, в) — отклонение, при котором профиль детали представляет собой многогранную фигуру с криволинейными гранями. Величина огранки определяется как наибольшее расстояние от точек действительного профиля до прилегающей окружности.

Бочкообразность, седлообразность (корсетность) и изогнутость являются следствием непрямолинейности образующих, конусность — следствием непараллельности образующих.

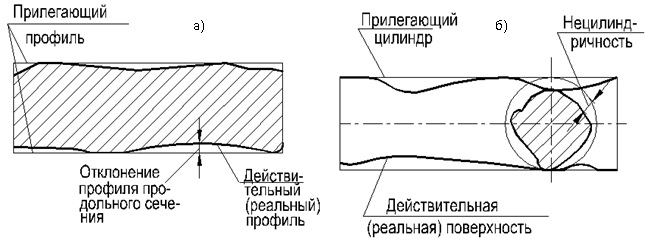
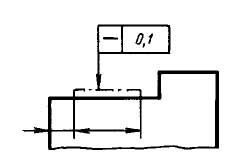
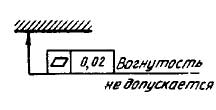
Совокупность всех отклонений профиля сечения плоских поверх¬ностей может быть охарактеризована комплексным показателем — непрямолинейностью, а всех отклонений формы поверхности — неплоскостностью. Непрямолинейность (отклонение от прямо-линейности про¬филя поверхности) — наибольшее расстояние от точек действительного профиля (полученного в сечении поверхности нормальной плоскостью, проходящей в задан-ном направлении) до прилегающей прямой (рис. 47, а). Допуск на непрямолинейность может быть отнесен ко всему участку проверяемой поверхности или к заданной длине. Неплоскост¬ность (отклонение от плоскостности) — наибольшее расстояние от точек действительной поверхности до прилегающей плоскости (рис. 47, б), Детали с плоскими поверхностями могут иметь дифференцированные отклонения в виде вогнутости (рис. 47, в) или выпуклости (рис. 47, г).

Отклонением расположения называется отклонение от номинального распо-ложения рассматриваемой поверхности, ее оси или плоскости симметрии относительно баз или отклонение от номинального взаимного расположения рассматриваемых поверхностей. Номинальное расположение определяется номинальными линейными и угловыми размерами между рассматриваемыми поверхностями, их осями или плоскостями симметрии.

Различают основные виды отклонений расположения:
непараллельность — отклонение от параллельности либо плоскости, либо оси поверхности вращения и плоскости. Непараллельность характеризуется раз-ностью наибольшего и наименьшего расстояний между плоскостью и осью по-верхности на заданной длине:
неперпендикулярность — отклонение от перпендикулярности плос¬костей, осей или оси к плоскости — отклонение угла между плоскостя¬ми, осями или осью и плоскостью от прямого угла, выраженное в линей¬ных единицах на заданной длине:

несоосность — отклонение от соосности относительно базовой повер¬хности — наибольшее расстояние между осью рассматриваемой поверх¬ности и осью базовой поверхности на всей длине рассматриваемой поверхности или расстояние между осями в заданном сечении.

Обычно на практике учитывают комплексные погрешности, которые складываются из погрешностей формы и положения. К таким погрешностям относятся:
радиальное биение — разность наибольшего Аmax и наименьшего Аmin расстояний от точек реальной поверхности до базовой оси вращения в сечении, перпендикулярном этой оси (рис. 48, а). Радиальное биение является результатом смещения центра (эксцентриситета) рассматривае¬мого сечения относительно оси вращения и некруглости;
торцевое биение — разность наибольшего и наименьшего расстоя¬ний а от точек реальной торцевой поверхности, расположенных на окружности заданного диаметра, до плоскости, перпендикулярной базовой оси вра¬щения (рис. 48, б).

Если диаметр не задан, то торцевое биение определяется на наибольшем диаметре торцевой поверхности. Торцевое биение является резуль¬татом неперпендикулярнос¬ти торцевой поверхности базовой оси и отклонений фирмы торца по линии измерения.

Источник

Допуск биения

В процессе изготовления деталей вращения согласно технологическому процессу их изготовление связанно с определённым количеством операций, которые предусматривают переустановку обрабатываемого материала. В ходе смены позиций заготовки из-за погрешности закрепляющих механизмов и других факторов, возникают осевые биения обрабатываемой детали. Допуск биения наносится на чертеже в виде наклонной стрелки и цифрового значения указывающего величину отклонения.

Коленчатые валы, изготавливаемые для различных двигателей, предназначены для преобразования рабочего движения поршней во вращение главного силового элемента машины. По конструкции валы представляют собой относительно не жёсткую геометрическую форму данного типа детали, которая в свою очередь воспринимает большие переменные нагрузки, вызывающие такие виды допустимых деформаций как кручение и изгиб с последующим возвратом к исходной форме в состоянии покоя.

К наиболее важным техническим параметрам относятся параллельность осей, отклонение от круглости, допуски цилиндричности, допуск биения и многое другое.

Контроль параметров коленчатого вала достаточно, ответственный и трудоемкий процесс. Поэтому для контроля разного рода характеристик, применяют специальные приборы и стенды, а так же мерительные устройства с электронной индикацией и специальными датчиками.

Источник

Допуски формы и расположения

Любая технологическая операция может быть выполнена с определенной точностью, а значит размеры полученной в результате обработки детали не будут идеальными, они могут колебаться в некотором диапазоне. Для того, чтобы выполнить условия собираемости и обеспечить надежную работу детали в заданных условиях необходимо задать допустимый интервал, в который должен попасть итоговый размер. Этот интервал может регламентировать не только линейные или диаметральные размеры, но и форму или взаимное расположение поверхностей.

Допуски формы и расположения назначаются конструктором исходя из условий сборки и особенностей работы детали в механизме.

Виды допусков формы

Отклонения и допуски формы

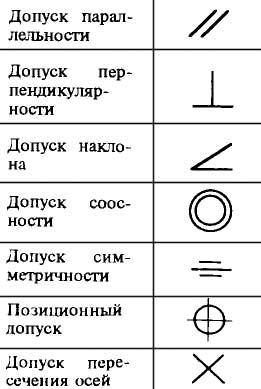
Различают следующие допуски на отклонения формы:

Допустимые отклонения обозначаются специальными символами.

Виды допусков расположения

Различают допуски месторасположения и допуски ориентации.

Отклонения и допуски расположения

Различают следующие виды допусков расположения:

Эти допуски обозначаются символами.

Суммарные допуски

Существует несколько видов суммарных допусков формы и расположения.

Эти допуски обозначаются символами.

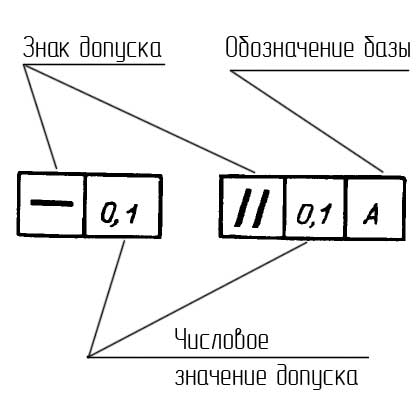
Обозначение допусков формы и расположения на чертежах

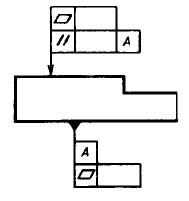
В случае отсутствия базы допуска рамка состоит только из двух частей. Примеры рамок допусков формы и расположения показаны на рисунке.

На рисунке слева показана рамка с допуском формы (допустимое отклонение от прямолинейности), справа с допуском расположения (допустимое отклонение от параллельности).

Рамку выполняют тонкими линиями. Высота текста в рамке должна равняться размеру шрифта размерных чисел. От рамки допуска до поверхности или до выноски проводится линия, оканчивающаяся стрелкой.

Перед числовым значение допуска могут указываться знаки:

Если допуск должен применяться не ко всей поверхности, а только к некоторому участку, то он обозначается штрих пунктирной линией.

Для одного элемента может быть указано несколько допусков, этом случае рамки изображаются одна над другой.

Дополнительная информация может быть указана над рамкой или под ней.

Информация о допусках формы и расположения может быть указана в технических требованиях.

Зависимые допуски

Зависимые допуски расположения обозначают следующим символом .

Этот символ может быть размещен после числового значения допуска, если зависимый допуск связан с действительными размерами рассматриваемого элемента. Также символ может быть размещен после буквенного обозначение (если оно отсутствует то в третьем поле рамки) в том случае, если зависимый допуск связан с действительными размерами базового элемента.

Назначение допусков формы и расположения

Чем точнее изготовлена деталь, тем более точные инструменты потребуются для ее изготовления и контроля размеров. Это автоматически увеличит ее стоимость. Получается, что цена изготовления детали во многом зависит от требуемой точности при ее изготовлении. Это означает, что конструктор должен указать лишь те допуски, которые действительно необходимы для сборки и надежной работы механизма. Допустимые интервалы также должны быть назначены исходя из условий собираемости и работоспособности.

В ГОСТе 24643-81 указаны рекомендации по назначению допусков формы и расположения поверхностей

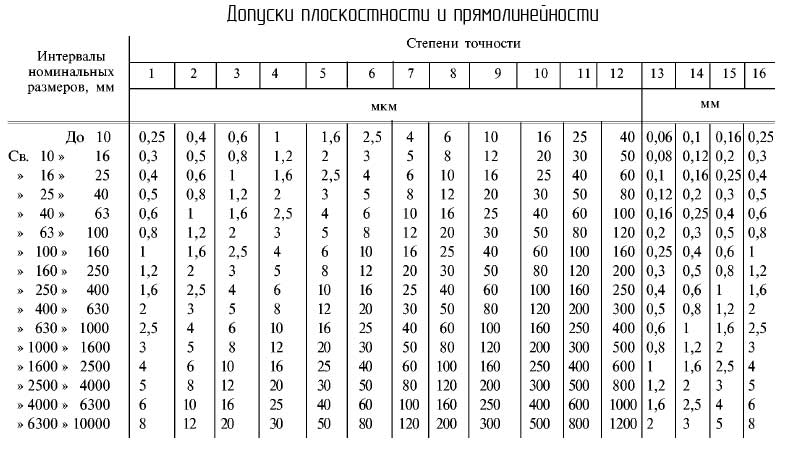
Числовые значения допусков формы

В зависимости от класса точности устанавливаются стандартные значения допусков формы.

Допуски плоскостности и прямолинейности

Номинальным размеров в данном случае считается номинальная длина нормированного участка.

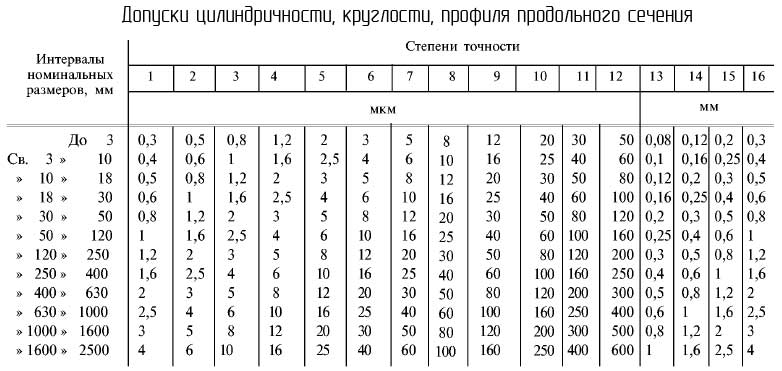
Допуски круглости, цилиндричности, профиля продольного сечения

Данные допуски назначаются в тех случаях, когда они должны быть меньше, чем допуск размера.

Номинальным размером считается номинальный диаметр поверхности.

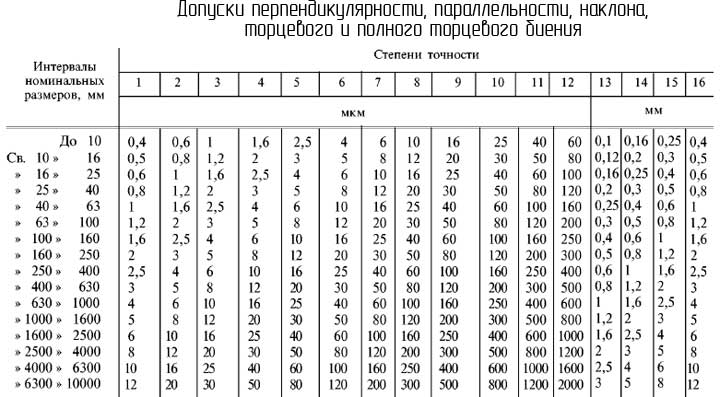
Допуски перпендикулярности, параллельности, наклона, торцевого биения

Номинальным размером при назначении допусков на параллельность, перпендикулярность, наклон понимается номинальная длина нормируемого участка или номинальная длина всей контролируемой поверхности.

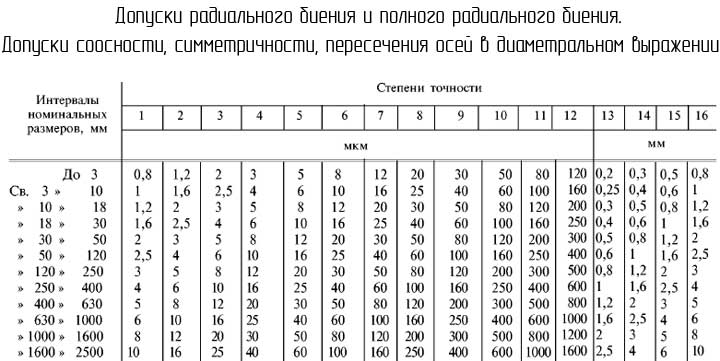
Допуски радиального биения, симметричности, соосности пересечения осей в диаметральном выражении

При назначении допусков радиального биения номинальным размером считается номинальный диаметр рассматриваемой поверхности.

В случае назначения допусков симметричности, пересечения осе соосности номинальным размером считается номинальный диаметр поверхности или номинальный размер между поверхностями, которые образуют рассматриваемый элемент.

Источник

Назначение допуска, выбор измерительных средств и измерение биения (стр. 1 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4

вала

«Назначение допуска, выбор измерительных средств и измерение биения

вала

Методические указания к лабораторно-практической работе «Наз­начение допуска, выбор измерительных средств и измерение радиаль­ного биения вала, установленного в центрах» по курсу «Взаимозаме­няемость, стандартизация и технические измерения» выполнены в соот­ветствии с учебным планом.

Методические указания рассмотрены и утверждены кафедрой:

Лабораторно-практическая работа «Назначение допуска, выбор измерительных средств и измерение радиа­льного биения вала «

Введение

При изготовлении деталей машин поверхности элемента детали получаются с отклонениями, как по форме так и по расположению одновременно. Параметры такого типа относят к числу комплексных в силу того, что они дают характеристику на базе нескольких дифференциальных ( например: отклонения от круглости + оклонения от соосности, отклонения от перпендикулярности + отклонения от плоскостности. ). Суммарную характеристику отклонений можно получить на основе анализа принятых типов биений. Комплексные характеристики очень удобны на выходном контроле, а вот для выяснения причин, полученного результата, необходимы дифференциальные.

Радиальное биение-разность наибольшего и наименьшего расстояний от точки реального профиля поверхности вращения до базовой оси в сечении плоскостью, перпендикулярной базовой оси.

Торцовое биение— разность наибольшего и наименьшего расстояний от точки реального профиля торцовой поверхности до плоскости, перпендикулярной базовой плоскости.

Рассмотренные биения обозначаются знаком рис. 1.

Рисунок 1.Знак биения и его параметры написания

Полное радиальное биение— разность наибольшего и наименьшего расстояний по всей реальной поверхности до базовой оси в пределах нормируемого участка.

Полное торцовое биение— разность наибольшего и наименьшего расстояний по всей реальной торцовой поверхности до плоскости, перпендикулярной базовой оси.

Для обозначения полных биений применяется знак рис. 2

Рисунок 2.Знак полных биений

В рассмотренных знаках: на первом месте проставляется собственно сам знак, на втором величина допустимого отклонения в мм и на третьем база, которая должно быть указана на детали и обозначена предписанным знаком (см. первую стр. обложки).

Методика и аппаратура для определения различных биений достаточно схожи и поэтому рассмотрение вопроса проведём на базе определения радиального биения вала установленного в центрах.

1.1Цель работы.

— назначения допусков формы на основе выбора допуска радиального биения;

— работы измерительными средствами при измерении биений поверхнос­тей тел вращения, установленных в центрах;

— выбора измерительных средств на основе сопоставления допускаемой погрешности измерения и предельной погрешности измерительного’ средства.

— с устройствами: индикаторов часового типа, рычажно-эубчатых инди­каторов и пружинных головок (микрокаторов);

— с устройством и конструкцией центровых контрольных базирующих

1.2. Задание:

Для предложенной детали (рис. 3) установить степень точности формы на указанных поверхностях, исходя из квалитета и предусмотреной геометриче­ской точности (А либо В либо С), табл. I.

По степени точности формы, выбрать допуск радиального биения, по табл. 2, и проставить его на эскизе детали см. рис.3 и рис 6., относительно принятых баз.

По известному квалитету изготовления поверхности определить до­пустимую погрешность измерения по табл.3. Выбрать средство измере­ния пользуясь табл.4. Выбор измерительного средства, провести на основе сопоставления допускае­мой погрешности измерения радиального биения и предельной погрешнос­ти измерительного средства.

Измерить величину радиального биения поверхности ва­ла, установленного в центрах по предложенной методике. Результаты анализа и измерений предс­тавить в отчете(см. приложение). Провести анализ полученных результатов и сделать заключения.

1.3.Пример:

В представленной детали рис.3, выполненной с относительной геометрической точностью В для поверхности Ø32е8, установить допуск радиаль­ного биения и выбрать средство измерения на основе сопоставления допускаемой погрешности измерения радиального биения и предельной погрешности измерительного средства. Дать заключение о годности поверхности детали и возможности исправления, при необходимости.

Квалитет допуска размера IT8, степень точности формы для относи­тельной геометрической точности В (по табл. I) будет 6.

Допуск радиального биения для Ø 32мм. и степени точности. 6 (по табл. 2)будет соответствовать 20 мкм.

Допуск погрешности измерений δ оценим по табл. 3: для квалитета IT8 детали Ø32мм он составит 10 мкм.

По табл. 4 определим предельную погрешность измерения

∆=10 мкм, имеет ин­дикатор часового типа с ценой деления 0,01мм при ходе измерительного стержня 0,02 мм.

Как видно, предельная погрешность δ не больше допуска погрешности измерений ∆, т. е. 10 мкм = 10 мкм, итак, данным инструментом можно проводить измерения.

0,001мм и погрешностью ∆= I мкм.

Рисунок 3. Деталь для анализа

ГОСТ 24643 рекомендует соотношения между допуском формы или расположения и допуском размера для всех видов допусков формы и расположения, предельных размеров по ГОСТ 25346.

Рекомендуемые относительные уровни геометрические точности

Квали-тет допуска размера

Уровни относи-тельной геомет-ричес-кой точнос-ти

Степень точнос-ти формы

Квали-тет допуска размера

Уровни относи-тельной геомет-ричес-кой точнос-ти

Степень точнос-ти формы

Квали-тет допуска размера

Уровни относи-тельной геомет-ричес-кой точнос-ти

Источник