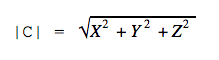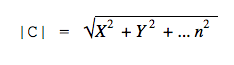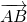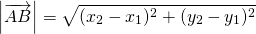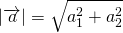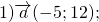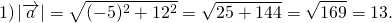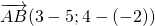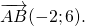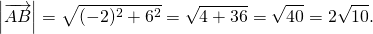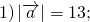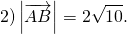Что такое длина вектора

Модуль вектора. Длина вектора.

Определение длины вектора

Для обозначения длины вектора используются две вертикальные линии слева и справа | AB |.

Формулы длины вектора

Формула длины вектора для плоских задач

В случае плоской задачи модуль вектора a = < a_x ; a_y > можно найти воспользовавшись следующей формулой:

Формула длины вектора для пространственных задач

В случае пространственной задачи модуль вектора a = < a_x ; a_y ; a_z > можно найти воспользовавшись следующей формулой:

Примеры задач на вычисление длины вектора

Примеры вычисления длины вектора для плоских задачи

Решение: | a | = √ 3 2 + (-4) 2 = √ 9 + 16 = √ 25 = 5.

Примеры вычисления длины вектора для пространственных задачи

Решение: | a | = √ 2 2 + 4 2 + 4 2 = √ 4 + 16 + 16 = √ 36 = 6.

Примеры вычисления длины вектора для пространств с размерностью большей 3

Решение: | a | = √ 1 2 + (-3) 2 + 3 2 + (-1) 2 = √ 1 + 9 + 9 + 1 = √ 20 = 2√ 5

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Источник

Операции с векторами

Как сложить и перемножить векторы (и зачем).

Мы постепенно показываем вам математику за пределами школьной программы. Начинали со знакомства с векторами, теперь сделаем следующий шаг.

Напомним основные мысли:

С векторами можно совершать некоторые математические операции. Вот о них и поговорим.

Правильно — векторы

Математики часто говорят во множественном числе «вектора», но по словарю правильно «векторы». Это такой профессиональный жаргон, как «договора», «бухгалтера» и «сервера». Мы будем использовать «векторы», но если вы окажетесь в постковидном математическом баре, лучше говорите «вектора».

Сложение

Представим четыре вектора, которые лежат в двухмерном пространстве и пока что не связаны между собой. Нарисуем эти векторы и обозначим их буквами X, Y, Z, K.

Поскольку векторы находятся в одном пространстве, координаты каждого состоят из одинакового количества чисел. У нас пример с двухмерным пространством и два числа. Выглядеть это будет так: X = (6, 4); Y = (3, −2); Z = (−7, −5); K = (−10, 4).

Векторы X, Y, Z, K в двухмерном пространстве

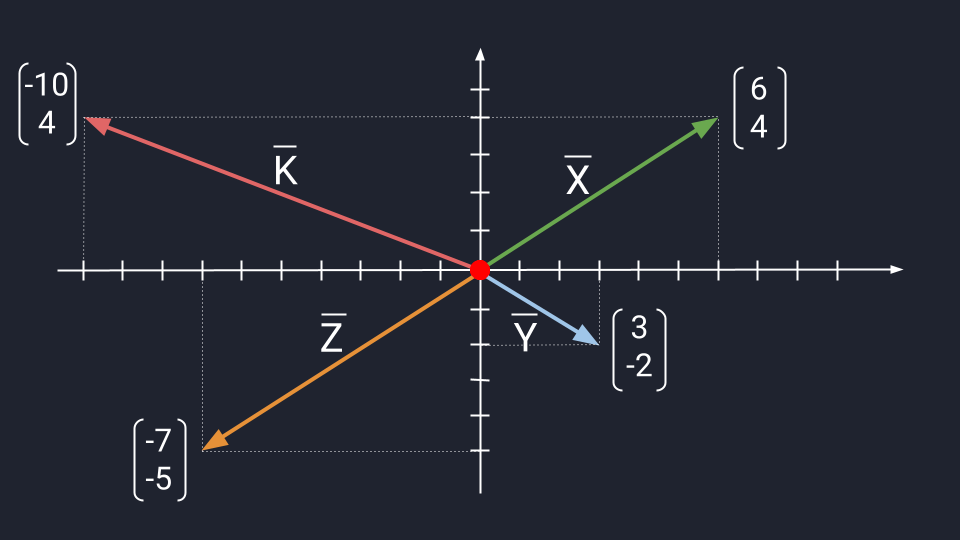
Если у нас несколько векторов с одинаковым количеством чисел, то эти числа можно поэлементно складывать. Для этого мы берём первое число одного вектора, складываем его с первым числом другого вектора и так далее.

Предположим, нам нужно сложить векторы X и Y.

X = (6, 4)
Y = (3, −2)
X + Y = (9, 2)

Вроде просто: складываешь последовательно все координаты, результаты сложения складываешь в исходные коробочки. Так можно делать с любым количеством координат. Помните, что вектор — это необязательно стрелка в двумерном пространстве. Она может быть и в десятимерном пространстве — с точки зрения математики это неважно.

Например, вот сложение векторов с пятью координатами:

Интуитивное изображение сложения

Для интуитивного восприятия удобно использовать векторы с двумя координатами. Их удобно рисовать на координатной плоскости и таким образом смотреть на геометрию.

Например, можно на плоскости показать, как будет работать сложение двух векторов. Для этого есть два метода: метод треугольника и метод параллелограмма.

Метод треугольника: ставим векторы Х и Y в очередь друг за другом. Для этого берём вектор Х, ставим за ним вектор Y и получаем новый вектор. Новый вектор начинается в хвосте вектора Х и заканчивается на стрелке вектора Y. Этот вектор — результат сложения. Представьте, что это ребёночек двух векторов.

Сложение векторов по методу треугольника: X = (6, 4); Y = (3, −2); Х + Y = (9, 2)

Чтобы воспользоваться методом параллелограмма, нам нужно поставить векторы Х и Y в одну исходную точку. Дальше мы дублируем векторы Х и Y, формируем параллелограмм и получаем новый вектор. В новом векторе соединяем исходную точку с исходной точкой дублирующих векторов — стрелка проходит посередине параллелограмма. Длина нового вектора — это сумма векторов Х и Y.

Сложение по методу параллелограмма и треугольника даёт одинаковый результат. Поэтому выбирайте вариант, который больше подходит под задачу.

Вычитание

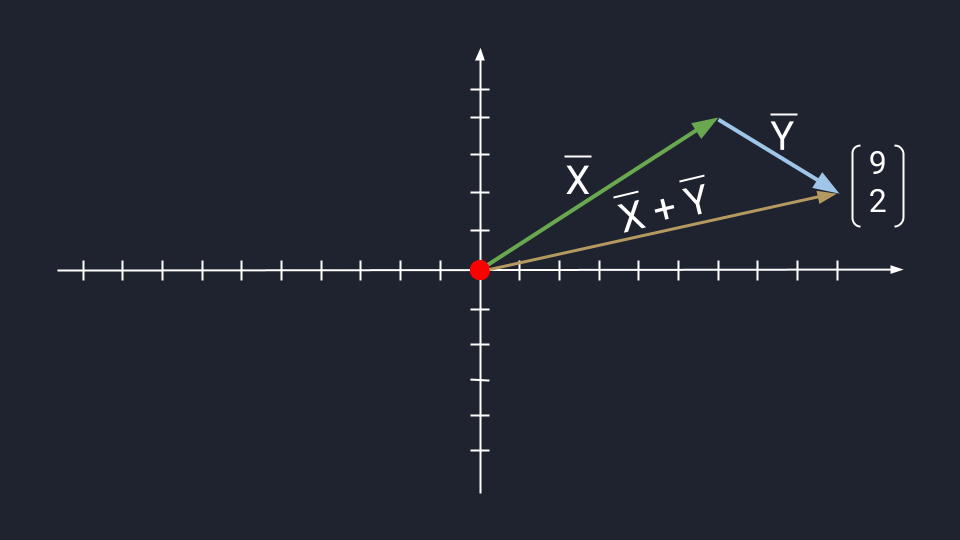
Вычитание векторов немного сложнее. Чтобы вычесть векторы, нужно «развернуть» вычитаемый вектор и сложить его с исходным. «Развернуть» — то есть направить в обратную сторону, «перевернув» знаки координат. Получится конструкция вроде такой: Х + (−Y)

Дальше используются правила сложения. Пошагово это выглядит так:

Теперь посмотрим, как выглядит вычитание векторов на графике:

Вычитание векторов по методу треугольника: X = (6, 4); −Y = (−3, 2); X + (−Y) = (3, 6) Вычитание векторов по методу параллелограмма: X = (6, 4); −Y = (−3, 2); X + (−Y) = (3, 6)

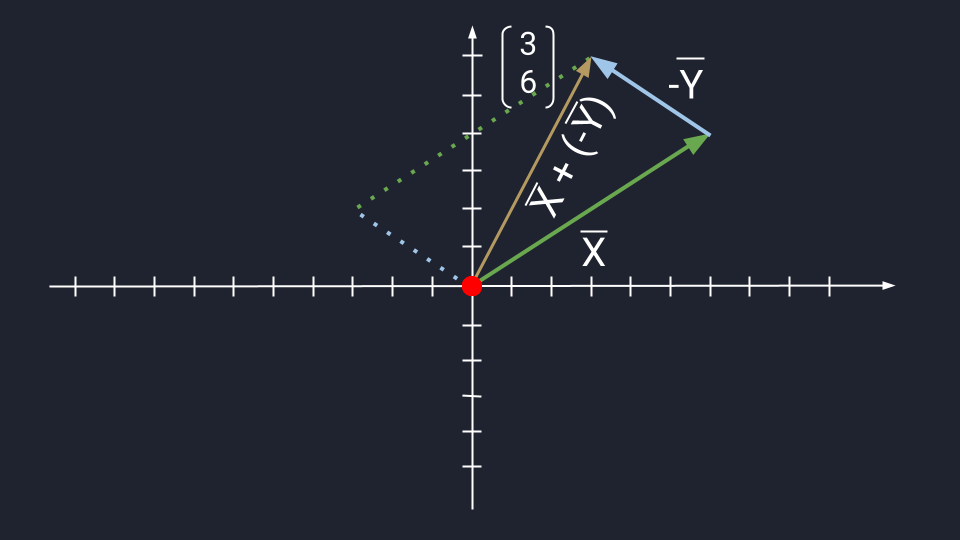
Длина вектора

Длина вектора — это одно число, которое измеряется расстоянием от кончика до стрелки вектора. Длину вектора нельзя путать с координатами. Координаты — это несколько чисел, которые указывают на расположение стрелки вектора. По координатам можно определить только конечную точку вектора. Например, если X = (6, 2), то стрелка будет находиться в точке 6 по оси Х. Или другой пример: если Y = (6, 5), то стрелка этого вектора будет находиться в точке 5 по оси Y.

Предположим, нам известны начальные точки векторов X и Y. Пусть это будет точка 2 по оси X и точка 2 по оси Y. Так мы можем легко посчитать длину отрезков:

X = 6 − 2 = 4
Y = 5 − 2 = 3

Иногда приходится рассчитывать длину третьего вектора, который привязан к двум другим векторам. Это легко сделать с помощью теоремы Пифагора — это когда квадрат гипотенузы равен сумме квадратов катетов. В нашем случае катетами будут длины векторов X и Y. Вспоминаем школьную формулу и считаем:

|C|2 = 42 + 32 = 25
|C| = √25 = 5 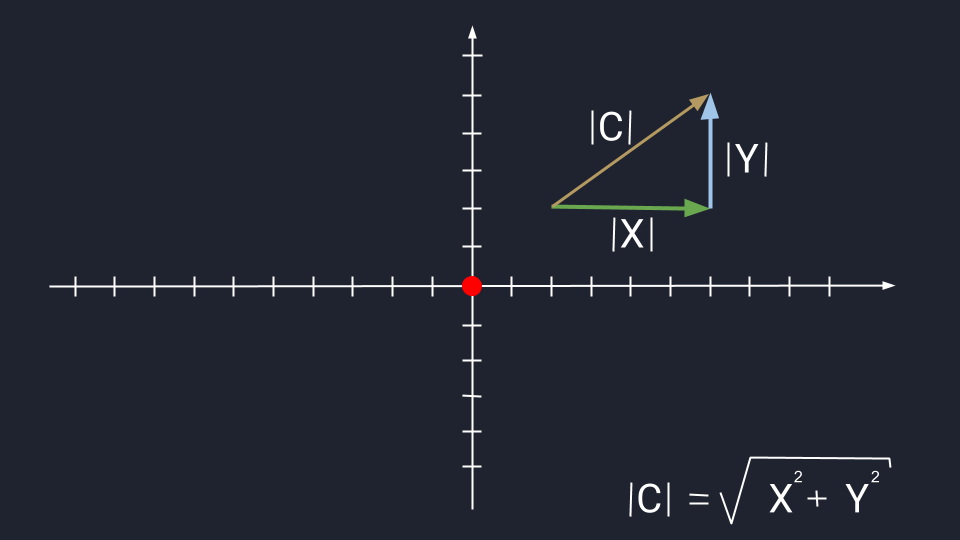Длина вектора считается по формуле прямоугольного треугольника. Чтобы было проще представить — перенесите векторы на систему координат

Это формула для двумерного пространства. В трёхмерном пространстве формула похожая: нужно сложить квадраты трёх координат и вычислить квадратный корень из суммы.

В пространстве с большим числом измерений формула выглядит сложнее, но по сути то же: складываем все квадраты координат и получаем квадратный корень из этой суммы.

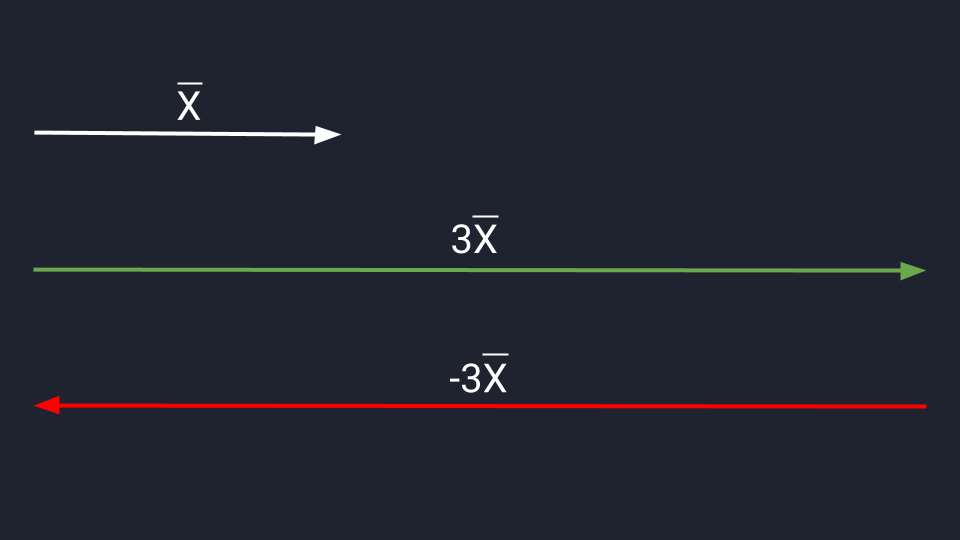
Умножение и деление вектора на число

Умножение и деление позволяют изменить длину и направление вектора. Если мы умножим вектор Х на три, то увеличим его длину в три раза. Если умножим на минус три — увеличим длину и изменим его направление на противоположное.

Умножение вектора на число

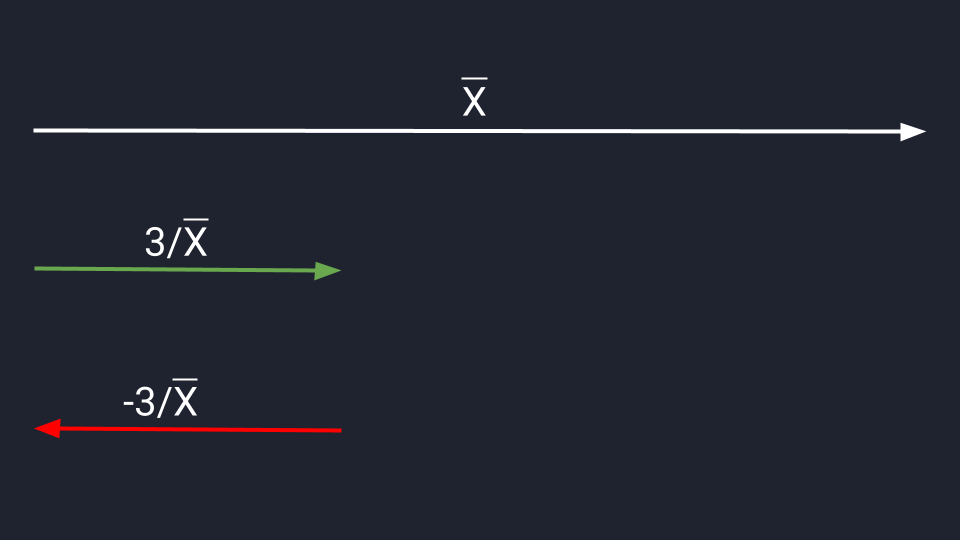
Для деления сохраняются аналогичные правила. Делим вектор Х на три и сокращаем длину в три раза. Делим на минус три — сокращаем и разворачиваем.

Деление вектора на число

Да вроде несложно!

Пока ничего сложного. Но если углубляться, вы узнаете, что:

Что дальше

В следующей статье рассмотрим линейную зависимость векторов. Чтобы не скучать — посмотрите интервью с Анастасией Никулиной. Анастасия сеньор-дата-сайентист в Росбанке и по совместительству блогер с интересной историей.

Источник

Длина вектора

Длина вектора (или модуль вектора или абсолютная величина вектора) — это длина отрезка, изображающего вектор.

с началом в точке A(x₁; y₁) и концом в точке B(x₂; y₂) длину находим по формуле расстояния между точками:

Соответственно, для вектора

(то есть длина вектора равна квадратному корню из суммы квадратов его координат).

Найти длину вектора:

2) Если нужно найти длину вектора, зная координаты его начала и конца, удобнее сначала найти координаты вектора:

Теперь найдём его длину:

Длина (модуль) нулевого вектора равна нулю.

Источник

Что такое длина вектора

Сформулируем ряд базовых определений.

Три вектора в пространстве называются компланарными, если они лежат в одной плоскости или на параллельных плоскостях. Если среди трех векторов хотя бы один нулевой или два любые коллинеарны, то такие векторы компланарны.

то есть модуль вектора равен корню квадратному из суммы квадратов его координат.

Обозначим углы между вектором и осями координат через α, β, γ соответственно. Косинусы этих углов называются для вектора направляющими, и для них выполняется соотношение: Верность данного равенства можно показать с помощью свойства проекции вектора на ось, которое будет рассмотрено в нижеследующем пункте 4.

Пусть в трехмерном пространстве заданы векторы своими координатами. Имеют место следующие операции над ними: линейные (сложение, вычитание, умножение на число и проектирование вектора на ось или другой вектор); не линейные – различные произведения векторов (скалярное, векторное, смешанное).

1. Сложение двух векторов производится покоординатно, то есть если

Геометрически два вектора складываются по двум правилам:

а) правило треугольника – результирующий вектор суммы двух векторов соединяет начало первого из них с концом второго при условии, что начало второго совпадает с концом первого вектора; для суммы векторов – результирующий вектор суммы соединяет начало первого из них с концом последнего вектора-слагаемого при условии, что начало последующего слагаемого совпадает с концом предыдущего;

б) правило параллелограмма (для двух векторов) – параллелограмм строится на векторах-слагаемых как на сторонах, приведенных к одному началу; диагональ параллелограмма исходящая из их общего начала, является суммой векторов.

Геометрически два вектора складываются по уже упомянутому правилу параллелограмма с учетом того, что разностью векторов является диагональ, соединяющая концы векторов, причем результирующий вектор направлен из конца вычитаемого в конец уменьшаемого вектора.

При λ>0 – вектор сонаправлен ; λ противоположно направлен ; | λ|> 1 – длина вектора увеличивается в λ раз; | λ| 1 – длина вектора уменьшается в λ раз.

4. Пусть в пространстве задана направленная прямая (ось l ), вектор задан координатами конца и начала. Обозначим проекции точек A и B на ось l соответственно через A ’ и B ’.

Рассмотрим некоторые основные свойства проекций:

1) проекция вектора на ось l равна произведению модуля вектора на косинус угла между вектором и осью, то есть ;

2.) проекция вектора на ось положительна (отрицательна), если вектор образует с осью острый (тупой) угол, и равна нулю, если этот угол – прямой;

3) проекция суммы нескольких векторов на одну и ту же ось равна сумме проекций на эту ось.

Сформулируем определения и теоремы о произведениях векторов, представляющих нелинейные операции над векторами.

5. Скалярным произведением векторов и называется число (скаляр), равное произведению длин этих векторов на косинус угла φ между ними, то есть

Теорема 2.2. Необходимым и достаточным условием перпендикулярности двух векторов является равенство нулю их скалярного произведения

Следствие. Попарные скалярные произведения единичных орт равны нулю, то есть

Отсюда следует условие перпендикулярности ненулевых векторов и :

С помощью скалярного произведения векторов находят работу постоянной силы на прямолинейном участке пути.

Решение. Вычислим модули векторов и их скалярное произведение по теореме (2.3):

Пример 2.10. Затраты сырьевых и материальных ресурсов, используемых на производство одной тонны творога, заданы в таблице 2.2 (руб.).

Какова общая цена этих ресурсов, затрачиваемых на изготовление одной тонны творога?

Примечание. Действия с векторами, осуществленные в примере 2.10, можно выполнить на персональном компьютере. Для нахождения скалярного произведения векторов в MS Excel используют функцию СУММПРОИЗВ( ), где в качестве аргументов указываются адреса диапазонов элементов матриц, сумму произведений которых необходимо найти. В MathCAD скалярное произведение двух векторов выполняется при помощи соответствующего оператора панели инструментов Matrix

Решение. Находим вектор перемещения, вычитая из координат его конца координаты начала

Угол φ между и находим по формуле (2.29), то есть

– перпендикулярен векторам и ;

– векторы образуют правую тройку (рис. 2.15).

Примечание. Определитель (2.25) раскладывается по свойству 7 определителей

Следствие 1. Необходимым и достаточным условием коллинеарности двух векторов является пропорциональность их соответствующих координат

Следствие 2. Векторные произведения единичных орт равны

Следствие 3. Векторный квадрат любого вектора равен нулю

Также с помощью векторного произведения можно определить момент силы относительно точки и линейную скорость вращения.

— перпендикулярен плоскости, проходящей через точки O , A , B ;

Следовательно, момент силы относительно точки O представляет собой векторное произведение

Решение. Найдем векторное произведение заданных векторов по формуле (2.32).

Теорема 2.6. Необходимым и достаточным условием компланарности трех векторов является равенство нулю их смешанного произведения

Теорема 2.7. Если три вектора заданы своими координатами, то их смешанное произведение представляет собой определитель третьего порядка, составленный из координат векторов- сомножителей соответственно, то есть

Объем треугольной пирамиды, построенной на этих же векторах, равен

Решение. Найдем координаты векторов

По формуле (2.36) объем пирамиды, построенной на векторах равен (единиц объема)

Рассмотрим очень важный вопрос о разложении вектора по базису. Приведем следующие определения.

получим выражение вектора через остальные векторы

Линейно независимыми называют векторы, если равенство (2.37) выполняется только тогда, когда все

Базисом n – мерного пространства E_n называют любую совокупность линейно независимых векторов n – мерного пространства.

Произвольный вектор n – мерного пространства можно представить в виде линейной комбинации векторов базиса таким образом:

Линейное пространство называется конечномерным и имеет размерность n , если в этом пространстве существует система из n линейно независимых векторов (базис) такая, что каждое ее расширение приводит к линейной зависимости системы.

Источник