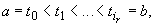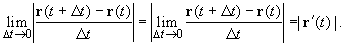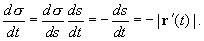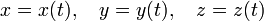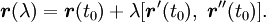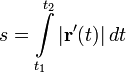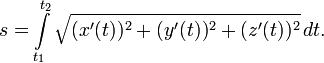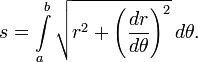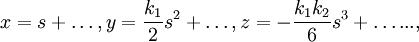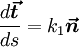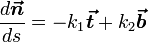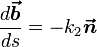Что такое длина кривой
Что такое длина кривой
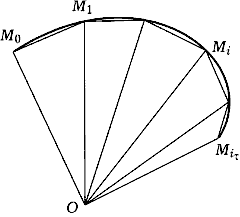
Рис. 93
называется его разбиением.
Пусть задана кривая
Г = <r(t); a 0, то 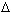





Левая и правая части этого неравенства имеют при 
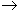
Замечание 2. Если непрерывно дифференцируемая кривая Г = <r(t); a 0.
А так как s(a) = 0, s(b) = SГ, то обратная функция t = t(s) однозначна, строго возрастает, непрерывно дифференцируема на отрезке [0,SГ] и
Таким образом, для всякой гладкой кривой ее параметр является строго возрастающей непрерывно дифференцируемой функцией переменной длины дуги и производная этой функции нигде не обращается в нуль.
Следовательно, функция t = t(s) есть допустимое преобразование параметра в смысле п. 17.1 и, следовательно, на гладкой кривой в качестве параметра можно взять переменную длину ее дуг. Из сказанного вытекает также, что имеет смысл производная
Замечание 5. Если кривая Г гладкая и в качестве параметра на ней взята переменная длина дуги s, 0
Длина дуги
Определение длины дуги гладкой кривой как интеграла от нормы производной эквивалентно определению
Численное интегрирование
Оценка по правилу Гаусса – Кронрода из 15 пунктов для этого интеграла от 1,570 796 326 808 177 отличается от истинной длины
Кривая на поверхности
Другие системы координат
Таким образом, для кривой, выраженной в полярных координатах, длина дуги равна
Таким образом, для кривой, выраженной в сферических координатах, длина дуги равна
Очень похожий расчет показывает, что длина дуги кривой, выраженная в цилиндрических координатах, равна
Дуги окружностей
Дуги больших кругов на Земле
Длины единиц расстояния были выбраны так, чтобы окружность Земли была равна 40 000 километров, или 21 600 морских миль. Это количество соответствующих угловых единиц за один полный оборот.
Эти определения метра и морской мили были заменены более точными, но исходные определения все еще достаточно точны для концептуальных целей и некоторых расчетов. Например, они подразумевают, что один километр равен точно 0,54 морской мили. Используя официальные современные определения, одна морская миля составляет ровно 1,852 километра [3], что означает, что 1 километр составляет примерно 0,539 956 80 морских миль. [4] Это современное соотношение отличается от рассчитанного по исходным определениям менее чем на одну часть из 10 000.
Длина дуги параболы
Античность
17 век
Интегральная форма
Основываясь на своей предыдущей работе с касательными, Ферма использовал кривую
которого касательной при х = имела наклон в
так что касательная линия будет иметь уравнение
что, когда решено, дает
Чтобы приблизиться к длине, Ферма суммировал бы последовательность коротких отрезков.
Длина дуги кривой
Понятие длины кривой.
Пусть кривая \(\Gamma\) задана уравнением кривой в векторной форме, и пусть на отрезке \([\alpha,\beta]\) выбраны точки \(t_
$$
\alpha=t_0 Рис. 22.3
Соединив последовательно точки \(M_<0>, \ M_<1>, \ \ldots, \ M_ _ _ _ Так как длина \(k\)-го звена ломаной \(\mathcal _ _ Если спрямляемая кривая \(\Gamma\) точкой \(M’\) разбита на кривые \(\Gamma_<1>\) и \(\Gamma_<2>\), то есть \(\Gamma=\Gamma_<1>\Gamma_<2>\), то кривые \(\Gamma_<1>\) и \(\Gamma_<2>\) спрямляемы, причем \(\circ\) Пусть \(P’\) и \(P″\) — произвольные ломаные, вписанные соответственно в \(\Gamma_<1>\) и \(\Gamma_<2>\), тогда \(P=P’P″\) — ломаная, вписанная в \(\Gamma\), причем Если кривая \(\Gamma\), заданная уравнением кривой в векторной форме, непрерывно дифференцируема, то она спрямляемая, а для ее длины \(S\) справедливо неравенство \(\circ\) Пусть \(T=\ Пусть кривая \(\Gamma=\<\textbf Тогда для любого \(t_<0>\in[\alpha,\beta]\) существует \(s'(t_<0>)\), причем \(\circ\) Пусть \(t_0+\Delta t\in[\alpha,\beta]\), \(M_0\) и \(M\) — точки кривой \(\Gamma\), соответствующие значениям \(t_<0>\) и \(t_<0>+\Delta t\) параметра кривой (рис. 22.4). Тогда длина дуги \(M_<0>M\) равна \(|\Delta s|\), где По теореме 1 получаем Из неравенств \eqref Заметим, что если \(\Delta t > 0\), то \(\Delta s\geq 0\), а если \(\Delta t Пусть кривая \(\Gamma\), заданная уравнением в векторной форме, является гладкой. Тогда функция \(\textbf Записать натуральное уравнение винтовой линии \(\triangle\) Кривая \(\Gamma\) является гладкой, так как вектор-функция \(\textbf Если параметром гладкой кривой \(\Gamma\) является переменная длина ее дуги \(s\), то \(\circ\) В самом деле, из формулы \eqref Вычисление длины кривой. Мы рассмотрели ряд вопросов, которые приводят к понятию определенных интегралов. Но есть и другой круг проблем, который приводит к понятию определенного интеграла. Они знают скорость изменения 1 суммы на другую величину, и им нужно найти первую величину, точнее, производную функции, но им нужно найти саму функцию, то есть данную функцию. 1 один из его примитивов. Эта задача решается с помощью конкретного интеграла. Это связано с тем, что такие примитивы являются, например, конкретным интегралом с переменной upper bound. As в качестве примера такой задачи рассмотрим расчет длины дуги кривой. Все они едины в том, что нахождение значения некоторых из этих величин привело к определению предела некоторой интегральной суммы, когда тонкость разбиения стремится к нулю, то есть к определенному интегралу. Людмила Фирмаль Если интегральная формула длины кривой стремится к нулю гранулярности соответствующего разбиения, то длина может быть выражена не только как верхний предел длины всех возможных пунктирных линий, вписанных на ней, но и как ее предел. Людмила Фирмаль Образовательный сайт для студентов и школьников Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника. © Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института Дифференциальная геометрия кривых — раздел дифференциальной геометрии, который занимается исследованием гладких пространственных и плоских кривых в евклидовом пространстве аналитическими методами. Наиболее общий способ задать уравнение пространственной кривой — параметрический: Часто удобно использовать инвариантную и компактную запись уравнения кривой с помощью вектор-функции: В зависимости от свойств дифференцируемости функций где y(x) и z(x) — дифференцируемые функции. Для того чтобы точка кривой, заданной общим уравнением (1), была обыкновенной (не особой точкой), достаточно, чтобы в этой точке выполнялось вышеуказанное неравенство Дифференциальная геометрия рассматривает также кусочно-гладкие кривые, которые состоят из гладких участков, разделённых особыми точками. В особых точках определяющие функции либо не удовлетворяют условиям регулярности, либо вообще не дифференцируемы. Важный класс кривых представляют плоские кривые, то есть кривые, лежащие в плоскости. Плоскую кривую также можно задать параметрически, первыми двумя из трёх уравнений (1). Другие способы: Функции Приведём примеры особых точек для плоских кривых. В применении к кривым это означает следующее: две кривые в общей точке имеют степень касания не ниже k-го порядка, если их производные в общей точке, до k-го порядка включительно, совпадают. Гладкая регулярная кривая в каждой точке имеет определённую касательную. Направление касательной в точке t0 кривой, задаваемой уравнениями (1), совпадает с направлением вектора Для плоской кривой уравнение касательной в точке Пусть В координатах оно имеет вид: Прямая, перпендикулярная касательной и проходящая через точку касания, называется нормалью к кривой. Плоскость, перпендикулярная касательной в данной точке кривой, называется нормальной плоскостью; все нормали для данной точки лежат в нормальной плоскости. Нормаль, лежащую в соприкасающейся плоскости, называют главной нормалью, а нормаль, перпендикулярная соприкасающейся плоскости, называется бинормалью. Направление главной нормали может быть получено как двойное векторное произведение: Для плоской кривой содержащая её плоскость совпадает с соприкасающейся. Нормаль, с точностью до знака, только одна — главная, и её уравнение в точке Центр соприкасающейся окружности называют центром кривизны, а радиус — радиусом кривизны. Радиус кривизны является величиной, обратной кривизне (см. ниже). Центр соприкасающейся окружности всегда лежит на главной нормали; отсюда следует, что эта нормаль всегда направлена в сторону вогнутости кривой. Геометрическое место центров кривизны кривой называется эволютой. Кривая, ортогонально пересекающая касательные кривой, называется эвольвентой. Построение эволюты и эвольвенты — взаимно обратные операции, то есть для эвольвенты данной кривой эволютой является сама кривая. Для измерения длины участка (дуги) произвольной кривой эта кривая заменяется ломаной, содержащей точки кривой как точки излома, и максимум длин всех таких ломаных принимается за длину кривой (рис. 3). В инвариантном виде формула для вычисления длины дуги (спрямления кривой) имеет вид: То же в декартовых координатах: В полярных координатах для плоской кривой: Кривая допускает бесчисленное множество различных способов параметрического задания уравнениями вида (1). Среди них особое значение имеет так называемая естественная параметризация, когда параметром служит длина дуги кривой, отсчитываемая от некоторой фиксированной точки. Среди преимуществ такой параметризации: При движении вдоль кривой её касательная меняет направление. Скорость этого вращения при равномерном, с единичной скоростью, движении вдоль кривой называется кривизной кривой. В случае параметрического задания кривой уравнениями (1) кривизна кривой определяется по формуле где Дважды дифференцируемая кривая в каждой точке, где кривизна отлична от нуля, имеет единственную соприкасающуюся плоскость. Для плоских кривых можно различать направление вращения касательной при движении вдоль кривой, поэтому кривизне можно приписывать знак в зависимости от направления этого вращения. Кривизна плоской кривой, задаваемой уравнениями При движении вдоль кривой в окрестности заданной точки соприкасающаяся плоскость вращается, причём касательная к кривой является мгновенной осью этого вращения. Скорость вращения соприкасающейся плоскости при равномерном, с единичной скоростью, движении называется кручением. Направление вращения определяет знак кручения. Трижды дифференцируемая кривая в каждой точке с отличной от нуля кривизной имеет определённое кручение. В случае параметрического задания кривой уравнениями (1) кручение кривой определяется по формуле Для прямой кручение не определено, поскольку неоднозначно определяется соприкасающаяся плоскость. Плоская кривая в каждой точке имеет кручение, равное нулю. Обратно, кривая с тождественно равным нулю кручением — плоская. Фигура, составленная из касательной, главной нормали и бинормали, а также из трех плоскостей, попарно содержащих эти прямые, называют естественным трёхгранником (трёхгранником Френе, см. рис. 4). Соприкасающаяся и нормальная плоскости уже упоминались; третья плоскость, содержащая касательную и бинормаль, называется спрямляющей. Если рёбра естественного трёхгранника в данной точке кривой принять за оси прямоугольной декартовой системы координат, то уравнение кривой в естественной параметризации раскладывается в окрестности этой точки в ряд по координате вдоль кривой: где k1 и k2 — кривизна и кручение кривой в указанной точке. Единичные векторы где дифференцирование идёт по дуге кривой. Формулы (2) называют формулами Френе́, или Френе-Серре. Будем рассматривать длину дуги заданной кривой как время, а трёхгранник Френе — как твёрдое тело, движущееся вдоль кривой. Тогда это движение в каждый момент времени состоит из поступательного (вдоль касательной) и мгновенного вращения с угловой скоростью Это означает, что вектор мгновенного вращения лежит в спрямляющей плоскости и распадается на 2 составляющие: вращение вокруг бинормали со скоростью k1 (поворот) и вращение вокруг касательной со скоростью k2 (кручение). Кривая с отличной от нуля кривизной полностью определяется (с точностью до положения в пространстве) заданием её кривизны и кручения как функций дуги s кривой. В связи с этим систему уравнения называют натуральными уравнениями кривой. Рассмотрим винтовую линию (рис. 4), заданную уравнениями: По вышеприведенным формулам получаем: Таким образом, кривизна и кручение винтовой линии постоянны. Поскольку натуральные уравнения однозначно определяют форму кривой, других кривых с постоянными кривизной и кручением не существует. Предельными случаями винтовой линии являются окружность (она получается при b = 0 ) и прямая ( a = 0 ). Длина дуги — Дифференциальная геометрия кривых раздел дифференциальной геометрии, который занимается исследованием гладких пространственных и плоских кривых в евклидовом пространстве аналитическими методами. Содержание 1 Способы задания кривой 1.1 Плоские… … Википедия Длина кривой — (или, что то же, длина дуги кривой) в метрическом пространстве числовая характеристика протяжённости этой кривой[1]. Исторически вычисление длины кривой называлось спрямлением кривой (от лат. rectificatio, спрямление). Если длина кривой… … Википедия ДЛИНА — 1) Длина отрезка прямой расстояние между его концами.2) Длина ломаной сумма длин ее звеньев.3) Длина дуги кривой предел длины вписанной в нее ломаной, когда число ее звеньев неограниченно возрастает, причем длина каждого звена стремится к нулю … Большой Энциклопедический словарь ДЛИНА — числовая характеристика протяженности линий в метрич. пространстве. Д. отрезка прямой расстояние между его концами, измеренное каким либо отрезком, принятым за единицу Д. Длина ломаной сумма Д. ее звеньев. Д. простой дуги точная верхняя грань… … Математическая энциклопедия ДЛИНА — числовая характеристика протяженности линий в метрич. пространстве. Д. отрезка прямой расстояние между его концами, измеренное каким либо отрезком, принятым за единицу Д. Длина ломаной сумма Д. ее звеньев. Д. простой дуги точная верхняя грань… … Математическая энциклопедия ДЛИНА — физ. величина, характеризующая протяжённость, удалённость и перемещение тел или их частей вдоль заданной линии. Единица измерения в СИ метр (м). Д. отрезка прямой расстояние между его концами. Д. дуги ломаной сумма длин её прямолинейных звеньев.… … Естествознание. Энциклопедический словарь Длина — Размерность L Единицы измерения СИ м СГС см … Википедия Длина — числовая характеристика протяжённости линий. В разных случаях понятие Д. определяется различно. 1) Д. отрезка прямой расстояние между его концами, измеренное каким либо отрезком, принятым за единицу Д. 2) Д. ломаной сумма Д. её звеньев.… … Большая советская энциклопедия Кручение кривой — Дифференциальная геометрия кривых раздел дифференциальной геометрии, который занимается исследованием гладких пространственных и плоских кривых в евклидовом пространстве аналитическими методами. Содержание 1 Способы задания кривой 1.1 Плоские… … Википедия
$$
\sigma_n=\sum_
$$
Если существует точная верхняя грань множества длин ломаных, вписанных в кривую \(\Gamma\), то эта грань называется длиной кривой \(\Gamma\). Кривая, имеющая длину, называется спрямляемой.
$$
S=S_<1>+S_<2>,\label
$$
где \(S, \ S_1, \ S_2\) — длины кривых \(\Gamma, \ \Gamma_1, \ \Gamma_2\) соответственно.
$$
\sigma=\sigma’+\sigma″,\label
$$
где \(\sigma,\sigma’,\sigma″\) — длины ломаных \(P, \ P’, \ P″\) соответственно. Так как \(\Gamma\) — спрямляемая кривая, то \(\sigma\leq S\), и поэтому
$$
\sigma’\leq S,\qquad \sigma″\leq S.\nonumber
$$
По теореме о точной верхней грани существуют \(\operatorname\sigma’, \ \operatorname\sigma″\), то есть \(\Gamma_<1>\) и \(\Gamma_<2>\) — спрямляемые кривые. Из равенства \eqref
$$
S_<1>+S_<2>\leq S.\label
$$
Докажем, что в \eqref
$$
S\leq (\beta-\alpha)\underset<\alpha\leq t\leq\beta><\operatorname
$$
$$
|\textbf
$$
Из непрерывности вектор-функции \(\textbf
$$
\exists \ C > 0:\quad\forall t\in [\alpha,\beta]\rightarrow |\textbf
$$
В качестве \(C\) можно в силу теоремы Вейерштрасса взять число
$$
C=\max_<\alpha\leq t\leq\beta>|\textbf
$$
Так как \(|r'(\tau_k)|\leq C\), то из \eqref
$$
\sigma_
$$
где число \(C\) определяется формулой \eqrefПроизводная переменной длины дуги.
$$
s'(t_<0>)=|\textbf
$$Рис. 22.4
$$
\Delta s=s(t_0+\Delta t)-s(t_0),\nonumber
$$
а длина хорды \(M_<0>M\) равна \(|\Delta \textbf
$$
|\Delta r|\leq|\Delta s|.\label
$$
$$
|\Delta s|\leq\max_
$$
где \(P\) — отрезок с концами \(t_<0>\) и \(t_<0>+\Delta t\).
$$
|\Delta \textbf
$$
откуда при \(\Delta t\neq 0\) получаем
$$
\vert \frac<\Delta \textbf
$$Натуральное уравнение гладкой кривой.
$$
t'(s)=\frac<1>
$$
Таким образом, функция \(t=t(s)\) является допустимым преобразованием параметра (замечания здесь и здесь), и уравнение кривой \(\Gamma\) можно записать в виде
$$
\textbf
$$
Если параметром кривой \(\Gamma\) является переменная длина ее дуги \(s\), то \(s\) называют натуральным параметром, а уравнение кривой \(\Gamma\)
$$
\textbf
$$
записанное через параметр \(s\), называют натуральным уравнением.
$$
x=a\cos t,\quad y=a\sin t,\quad z=bt,\quad 0\leq t\leq T,\nonumber
$$
где \(a > 0, \ b > 0\).
$$
|\textbf
$$
По формуле \eqref
$$
\frac
$$
откуда заключаем (следствие 2 из теоремы Лагранжа), что
$$
s=t\sqrt
$$
где \(B=0\), так как \(s(0)=0\). Следовательно, \(t=\displaystyle \frac<\sqrt
$$
x=a\cos \frac<\sqrt<\sqrt
$$
так как длина \(S\) кривой \(\Gamma\) равна \(s(T)=T\sqrt
$$
\left|\frac
$$Вычисление длины кривой






Вычисление длины кривой
Длина дуги кривой
Содержание
Способы задания кривой
(1), 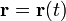
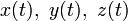
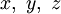
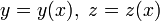
Плоские кривые
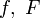
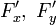
Соприкосновение
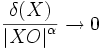
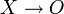
Касательная
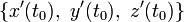
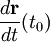
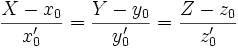
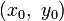
Соприкасающаяся плоскость и нормали
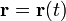
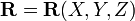
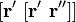
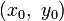
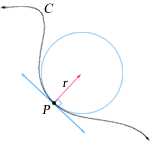
Соприкасающаяся окружность
Длина дуги кривой
Параметризация
Кривизна
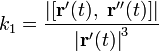
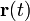
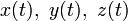
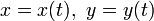
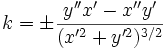
Кручение
Формулы Френе
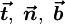
(2) Кинематическое истолкование
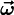
Натуральные уравнения кривой
Пример
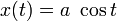
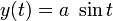
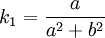
См. также
Литература
Полезное
Смотреть что такое «Длина дуги кривой» в других словарях: