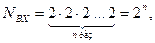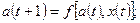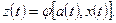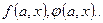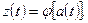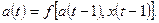Аналоговые, дискретные и цифровые сигналы

Любая физическая величина по характеру изменения ее значения может быть постоянной (если она имеет только одно фиксированное значение), дискретной (если она может иметь два или более фиксированных значений), или аналоговой (если она может иметь бесчисленное множество значений). Все эти величины могут быть преобразованы в цифровую форму.

Аналоговым называется такой сигнал, который может быть представлен непрерывной линией из множества значений, определенных в каждый момент времени относительно временной оси.

Значения аналогового сигнала произвольны в каждый момент времени, поэтому он может быть в принципе представлен как некая непрерывная функция (зависящая от времени как от переменной) либо как кусочно-непрерывная функция времени.

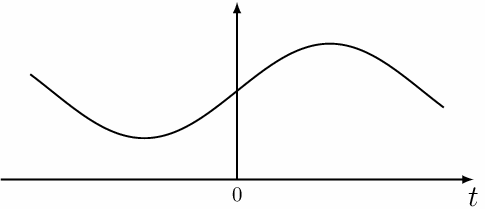
Аналоговым сигналом можно назвать, например, звуковой сигнал, генерируемый обмоткой электромагнитного микрофона или ламповым акустическим усилителем, поскольку такой сигнал непрерывен и его значения (напряжение или ток) сильно отличаются друг от друга в каждый момент времени.

На приведенном ниже рисунке изображен пример подобного рода аналогового сигнала.

Аналоговые величины могу иметь бесконечное множество значений в определенных пределах. Они непрерывны и их значения не могут изменяться скачками.

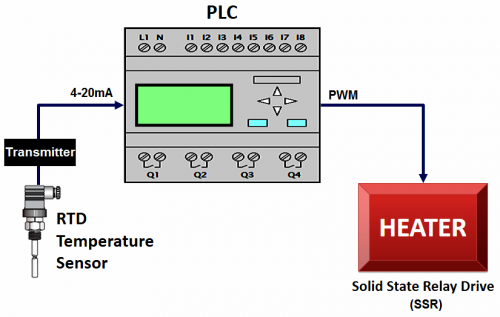
Пример аналогового сигнала: термопара передает в аналоговом виде значение температуры в программируемый логический контроллер, который управляет с помощью твердотельного реле температурой в электрической печи.

Если некий сигнал принимает произвольные значения лишь в отдельные моменты времени, то такой сигнал называют дискретным. Чаще всего на практике применяются дискретные сигналы, распределенные по равномерной временной решетке, шаг которой называется интервалом дискретизации.

Дискретный сигнал принимает определенные не нулевые значения лишь в моменты дискретизации, то есть он является не непрерывным в отличие от аналогового сигнала. Если из звукового сигнала вырезать небольшие кусочки определенного размера через равные интервалы, такой сигнал можно будет назвать дискретным.

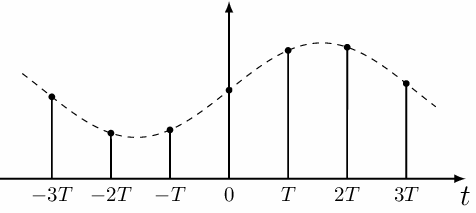
Ниже приведен пример формирования подобного дискретного сигнала с интервалом дискретизации Т. Обратите внимание, что квантуется лишь интервал дискретизации, но не сами значения сигнала.

Дискретные сигналы имеют два и более фиксированных значений (количество их значений всегда выражается целыми числами).

Когда дискретный сигнал принимает только какие-то фиксированные значения (которые могут быть расположены по сетке с определенным шагом), такие что они могут быть представлены как количество квантовых величин, такой дискретный сигнал называется цифровым. То есть цифровой сигнал — это такой дискретный сигнал, который квантован не только по промежуткам времени, но и по уровню.

Практически дискретные и цифровые сигналы в ряде задач отождествляются, и могут быть легко заданы в форме отсчетов с помощью вычислительного устройства.

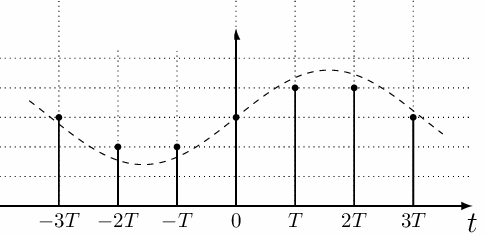
На рисунке приведен пример формирования цифрового сигнала на базе аналогового. Обратите внимание, что значения цифрового сигнала не могут принимать промежуточных значений, а только определенные — целое количество вертикальных шагов сетки.

Цифровой сигнал легко записывается и перезаписывается в память вычислительных устройств, просто считывается и копируется без потери точности, тогда как перезапись аналогового сигнала всегда сопряжена с утратой некоторой, пусть и незначительной, части информации.

Обработка цифровых сигналов позволяет получать устройства с очень высокими характеристиками благодаря выполнению вычислительных операций совершенно без потерь качества, либо с пренебрежимо малыми потерями.

В силу этих достоинств, именно цифровые сигналы повсеместно распространены сегодня в системах хранения и обработки данных. Вся современная память — цифровая. Аналоговые носители информации (такие как пленочные кассеты и т.д.) давно ушли в прошлое.

Аналоговый и цифровой приборы для измерения напряжения:

Но даже у цифровых сигналов есть свои недостатки. Их невозможно передать напрямую как есть, ибо передача обычно реализуется посредством непрерывных электромагнитных волн. Поэтому при передаче и приеме цифровых сигналов необходимо прибегать к дополнительной модуляции и аналого-цифровому преобразованию. Меньший динамический диапазон цифровых сигналов (отношение наибольшего значения к наименьшему), обусловленный квантованностью значений по сетке, является еще одним их недостатком.

Существуют и такие области, где аналоговые сигналы незаменимы. Например аналоговый звук никогда не сравнится с цифровым, поэтому ламповые усилители и пластинки до сих пор не выходят из моды, несмотря на обилие цифровых форматов записи звука с самой высокой частотой дискретизации.

Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!

Подписывайтесь на наш канал в Telegram!

Просто пройдите по ссылке и подключитесь к каналу.

Не пропустите обновления, подпишитесь на наши соцсети:

Источник

Понятие о дискретных устройствах

Общие сведения о дискретных устройствах

Простейшим элементом дискретного действия является реле или релейный элемент.

Под реле или релейным элементом понимается элемент, обладающий релейной (кусочно-линейной) характеристикой, при которой изменение входной величины x вызывает скачкообразное выходной величины z, принимающей лишь несколько дискретных значений. В большинстве случаев используются двузначные элементы, у которых выходной сигнал принимает только два значения, например 0 или 1 (Рисунок 1.1).

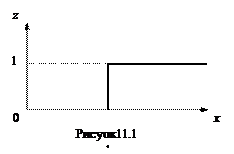
Таким образом, релейным элементом (РЭ) называется устройство, в котором при плавном или скачкообразном изменении входного сигнала выходной сигнал изменяется скачком.

В зависимости от физических явлений, положенных в основу конструкции релейных элементов, входными сигналами могут быть:

— ток или напряжение (электромагнитное реле);

— механическое усилие (кнопки, выключатели);

— давление жидкости или газа (гидравлические или пневматические реле);

— световое излучение (фотореле) и т.д.

Любой релейный элемент состоит из реагирующего органа (РО) и исполнительного органа (ИО), которые выполняют различные функции (Рисунок 1.2). РО служит для восприятия входного сигнала, ИО – для формирования выходного сигнала.

Названные органы могут быть или явно выражены, или объединены друг с другом. Примером четкого разделения органов служит электромагнитное реле, у которого обмотка является реагирующим органом, а контакты – исполнительными.

В бесконтактных релейных элементах нет явного разделения реагирующих и исполнительных органов. Под воздействием входного сигнала у этих элементов изменяются значения сопротивления выходной цепи или выходное напряжение.

Следует различать два уровня входных сигналов: высокий и низкий. При высоком уровне входного сигнала скачкообразно изменяется исходное состояние ИО, т.е. срабатывает РЭ. При низком уровне входного сигнала ИО остается в исходном состоянии или скачкообразно возвращается в него, т.е. происходит отпускание РЭ.

Условимся, что высокому уровню входного сигнала будет соответствовать символ «1», а низкому – символ «0». При изменении состояния ИО меняется его проводимость и уровень выходного сигнала. Высокому значению выходного сигнала будет соответствовать символ «1», а низкому – «0».

Таким образом, у релейных элементов как входные, так и выходные сигналы могут принимать лишь два значения (0 и 1). Величины, принимающие лишь два значения, носят название двоичных переменных. Следовательно, функционирование любых РЭ может быть описано двоичными переменными, т.е. алгеброй логики.

Отметим, что релейный элемент может находиться в различных состояниях (позициях), которые могут быть устойчивыми и неустойчивыми.

Под устойчивым состоянием (позицией) будем понимать такое состояние элемента (прежде всего его исполнительных органов), которое сохраняется до тех пор, пока не будет соответствующим образом изменено входное воздействие. Если же элемент при неизменном входном воздействии стремится перейти в новое состояние (позицию), то такое состояние (позицию) будем называть неустойчивым.

Совокупность взаимодействующих между собой релейных элементов образует дискретное (релейное) устройство ДУ (РУ), которое можно рассматривать как ориентированный (n, m)-полюсник с n входами и m выходами.

В дискретном устройстве, как и в релейном элементе, можно выделить:

— реагирующую (управляющую) часть – приемные элементы, непосредственно реагирующие на поступающие извне воздействия;

— исполнительную (управляемую) часть – исполнительные элементы (цепи), создающие сигналы на выходах ДУ;

— промежуточную часть – элементы, зависящие как от входных сигналов, так и друг от друга и осуществляющие, как правило, запоминание поступающих сигналов и их последовательностей.

Кроме этого в дискретном устройстве можно выделить вспомогательную часть, включающую различные детали, элементы и цепи, которые непосредственно не влияют на переработку или передачу информации, но обеспечивают правильное действие устройства, согласование отдельных его частей и формирование параметров сигналов. В нее входят источники питания, усилители, повторители и т.п.

Модель дискретного (релейного) устройства, отражающую только его свойства по переработке сигналов, называют дискретным автоматом (ДА), который представляет собой дискретное устройство без вспомогательной части.

Отметим, что под моделью обычно понимают упрощенное представление действия исследуемой системы, которое с одной стороны, обеспечивает достаточно точное отражение важнейших свойств системы, с другой стороны, является достаточно простым, доступным для изучения. Таким образом, ДА – это математическая модель ДУ.

Отметим также, что в инженерной практике термины «релейное устройство», «дискретное устройство», «дискретный автомат» сплошь и рядом отождествляются. В нашей дисциплине мы тоже их различать не будем.

Схематично дискретный автомат может быть изображен «черным ящиком» с n входами x₁, x₂, …, x_n и m выходами z₁, z₂, …, z_m (Рисунок 1.3). Входы x₁, x₂, …, x_n образуют множество (алфавит) входов (входных сигналов) дискретного автомата

выходы z₁, z₂, …, z_m – множество (алфавит) выходов (выходных сигналов) автомата

В дискретных устройствах (автоматах) в качестве промежуточной части могут присутствовать специальные релейные элементы, которые способны сохранять свое состояние или выходной сигнал после того, как входной сигнал, вызвавший переход в это состояние, перестал действовать. Для вторичного изменения состояния элемента или возврата в исходное состояние требуется новое входное воздействие. Обычный же релейный элемент при снятии входного воздействия скачком возвращается в исходное состояние.

Такие специальные релейные элементы называются элементами памяти (ЭП). Типичными представителями элементов памяти являются широко применяемые в дискретных устройствах триггеры различных типов.

Элементы памяти ДА принято выделять в отдельный блок, который называется блоком памяти или просто памятью дискретного автомата (Рисунок 1.4).

Часть схемы автомата, не содержащая элементов памяти, называется логическим преобразователем автомата или комбинационным блоком автомата.

В общем случае блок памяти дискретного автомата может содержать k элементов памяти y₁, y₂, …, y_k, каждый из которых может принимать некоторое конечное число состояний. Элементы y₁, y₂, …, y_k образуют множество элементов памяти автомата

Значение переменной y_i будем отождествлять с состоянием обозначаемого этой переменной элемента памяти. Состояние каждого ЭП однозначно определяет выходной сигнал, формируемый им. Поэтому для обозначения сигналов, формируемых элементами памяти, можно использовать те же буквы, которые обозначают элементы памяти, а множество

в необходимых случаях будем рассматривать как множество (алфавит) выходов (выходных сигналов) блока памяти автомата.

Безусловно, такое отождествление допустимо только в том случае, если элементы памяти ДА имеют по одному выходу либо пару противоположных выходов – так называемый парафазный выход.

Логический преобразователь ДА помимо формирования выходных сигналов автомата обеспечивает управление блоком памяти дискретного автомата. Для этого он имеет l выходов управления памятью (u₁, u₂, …, u_l), которые образуют множество (алфавит) выходов управления памятью

Выходы логического преобразователя непосредственно соединяются с соответствующими входами блока памяти автомата. Поэтому множество U называют еще множеством входов управления памятью дискретного автомата. В общем случае l ≥ k, так как каждый автомат памяти может иметь один или несколько управляющих входов. Так, при построении памяти автомата на RS-триггерах мощность множества U в два раза превышает мощность множества Y, т.е. l = 2k, так как каждый RS-триггер имеет 2 управляющих входа.

Таким образом, по функциональному признаку логический преобразователь ДА условно можно представить в виде двух отдельных блоков: блока формирования выходных сигналов и блока управления памятью (Рисунок 1.5). Заметим, что в реальных ДА иногда не удается выделить отдельно блок формирования выходных сигналов и блок управления памятью, так как указанные блоки могут иметь общие элементы, что упрощает конструкцию автомата в целом.

В настоящее время наибольшее распространение получили дискретные автоматы, сигналы в которых принимают только два возможных значения. Эти значения при математическом описании отождествляются с цифрами 0 и 1.

Совокупность значений входных сигналов называется входным набором ДА или состоянием входов. Так как каждый входной сигнал дискретного автомата может принимать одно из двух возможных значений независимо от значений других входов, то максимальное число различных наборов определится как произведение, состоящее из n цифр 2:

где n – число входов.

Совокупность значений выходных сигналов ДА называется выходным набором автомата или состоянием выходов.

В общем случае входные сигналы и состояния элементов памяти дискретного автомата определяют состояние автомата. Состояния элементов памяти определяют внутреннее состояние автомата.

Совокупность состояний ДА образует множество состояний автомата A = <a₁, a₂, …, a_μ>, из которых A₀ является начальным.

Дискретные автоматы преобразуют дискретные сигналы и сами могут изменять свое состояние только в дискретные моменты времени. Для описания функционирования дискретных автоматов вводится шкала дискретного или автоматного времени, единицей измерения которого является такт.

Тактом работы ДА называется отрезок времени произвольной длительности, в течение которого состояние автомата остается неизменным. Такты работы ДА с памятью делятся на устойчивые и неустойчивые. Такт называется устойчивым, если очередное изменение состояния дискретного автомата происходит только за счет изменения состояния входов, т.е. после поступления нового входного набора. Такт называется неустойчивым, если очередное изменение состояния дискретного автомата происходит только за счет изменения состояния памяти автомата.

Таким образом, устойчивый такт всегда предшествует моменту изменения входного набора автомата, а неустойчивый такт – моменту изменения состояния памяти дискретного автомата.

Функционирование автомата рассматривается в дискретные моменты времени t₁, t₂, …, t_i, которые называются тактовыми моментами. Предполагается, что поведение автомата не зависит от интервала времени между t_i и t_{i + 1}. Таким образом, фактически переменной величиной является не само время, а порядковые номера тактовых моментов, которые принято обозначать числами натурального ряда t = 0, 1, 2, …, i.

Именно эта последовательность номеров тактовых моментов образует дискретное или автоматное время, реальная же длительность тактов может быть произвольной.

В теории дискретных автоматов принимается допущение, что переход ДА из одного внутреннего состояния в другое осуществляется скачкообразно, т.е. мгновенно.

В реальных же автоматах имеет место всегда конечная длительность переходных процессов, о чем будет сказано ниже.

Итак, дискретный автомат является дискретным преобразователем информации.

Процесс функционирования автомата заключается в том, что при подаче на его вход некоторой последовательности сигналов он переходит из одного состояния в другое и формирует последовательность выходных сигналов.

Таким образом, для задания ДА фиксируют три конечных множества (алфавита):

— множество возможных входных сигналов

— множество возможных выходных сигналов

— множество возможных состояний автомата

На этих множествах задают две функции:

— функцию переходов f, определяющую состояние автомата a(t + 1) в момент дискретного времени t + 1 в зависимости от состояния автомата a(t) и значения входного сигнала x(t) в момент времени t:

— функцию выходов φ, определяющую зависимость выходного сигнала автомата z(t) от состояния автомата a(t) и входного сигнала x(t) в момент времени t:

Кроме того, на множестве состояний автомата фиксируют одно из внутренних состояний a₀ в качестве начального. Переменную t в записи часто опускают, применяя упрощенную форму записи:

Автоматы, функция выхода которых задается в таком виде, называются автоматами Мили. Выходной сигнал автомата Мили определяется состоянием автомата и значением входного сигнала в тот же момент времени.

На практике часто встречаются автоматы, выходной сигнал которых в момент времени t однозначно определяется состоянием автомата в этот же момент времени и не зависит от значения входного сигнала. Такие автоматы называются автоматами Мура.

Как следует из приведенных формул, выходной сигнал z(t) автомата Мура в момент времени t зависит от входного сигнала x(t – 1) в момент времени t – 1, так как

Источник

Теория дискретных устройств

Вы будете перенаправлены на Автор24

Теория дискретных устройств — это теоретические положения анализа и синтеза дискретных устройств, используемых для автоматизации технологических процессов.

Дискретные устройства

Под дискретным устройством понимается техническое оборудование, которое может быть различных физических типов. С математической точки зрения дискретное устройство считается логической функцией. В управляющей системе дискретное устройство работает как преобразователь информации, материальным отображением которой являются сигналы. Сегодняшняя вычислительная техника, основана на использовании дискретных устройств, которые в отдельных случаях могут быть релейными (иначе цифровые автоматы). В обобщённом смысле дискретное устройство — это технический модуль, который предназначен для выполнения определённых преобразований по заданному алгоритму над поступающими на его вход дискретными сигналами, и формировании из них выходной дискретной информации.

Дискретные устройства имеют определённые преимущества относительно устройств аналогового типа. А именно это:

Помимо отмеченных выше достоинств, у дискретных устройств есть ещё одно свойство, а именно способность осуществлять разные операции алгебры логики. Это даёт возможность повсеместного их применения в различных автоматических и автоматизированных управляющих и контрольных системах. Весь этот класс устройств возможно классифицировать как автоматизированные системы контроля и управления (АСКУ). Главным составляющим компонентом в структуре таких систем, включая и цифровые электронные вычислительные машины, считаются дискретные устройства.

История развития теории дискретных устройств и их эволюция

Рассмотрим кратко историю развития собственно дискретных устройств и научной дисциплины о них. В ряду выдающихся достижений и открытий первой половины девятнадцатого века довольно скромное место занимали электромагнитные реле, которые выполняли сначала формирование электрического телеграфного сигнала и получили своё наименование от слова французского языка «relais». Дословно этот термин означал «перегрузочный пункт», «пункт замены лошадей». Мало кто предполагал тогда, что это неприметное реле позднее окажется зародышем огромной технической отрасли, базой дискретных автоматических систем, телемеханических устройств, систем связи и отправной точкой прогресса средств вычислительной техники.

Готовые работы на аналогичную тему

Помимо электрических реле, были сконструированы механические, пневматические и гидравлические модификации реле. Прогресс радиоэлектронной отрасли привёл к изобретению электронной вакуумной лампы, а позднее полупроводников, магнитного и другого оборудования, которое обладало возможностями аналогичными реле, но без наличия в их структуре механических элементов и контактов. Все эти модули были названы бесконтактными элементами релейного типа. В дальнейшем появилась микроэлектроника и интегральные микросхемы. Проектирование интегральных микросхем состоит в создании самого большого числа компонентов, связанных функционально, и их связей в завершённой конструктивной реализации посредством единого комплекса технологических процессов. Сформированный при этом набор компонентов и их взаимосвязей и является интегральной схемой. Появление интегральных схем явилось, по своей сути, революционным преобразованием в сфере электроники. Сегодня подавляющее число электронных управляющих систем, контрольных и передающих систем выполняются на основе интегральных схем, которые стали главной элементной базой.

Последующая модернизация микроэлектронных элементов вызвала изобретение больших интегральных схем (БИС). Эти элементы имели сравнительно небольшой объём, но могли заменить работу десятков, а иногда и сотен реле.

Прогресс релейной техники, радиоэлектронных дискретных модулей требовал соответствующего теоретического обоснования. Нужно было сформировать теоретическое обоснование законов создания автоматических систем на базе дискретных элементов, выработать способы изучения дискретных устройств, специальную математическую поддержку.

Теория дискретных устройств

Несмотря на то, что теория дискретных устройств в качестве научного направления развивается ещё с окончания тридцатых годов прошлого века, вплоть почти до настоящего времени специалисты при разработке структурной организации дискретных модулей, использовали больше методы интуиции, способы графической проверки и так далее. Формирование схемы было почти искусством, которым обладали далеко не все, а только избранные.

Теория дискретных устройств занимается решением следующих задач:

Основой теории дискретных устройств является специальный математический аппарат, опирающийся на математическую логику, а именно булеву алгебру.

Булева алгебра названа так в честь её основателя Джона Буля, который первым ввёл понятия логического нуля и логической единицы.

Источник