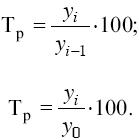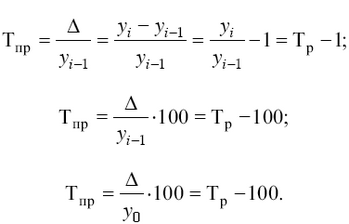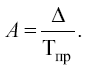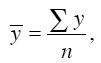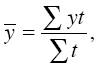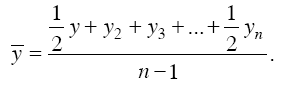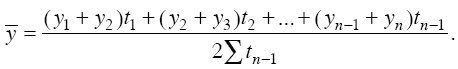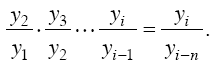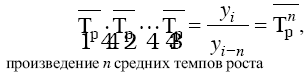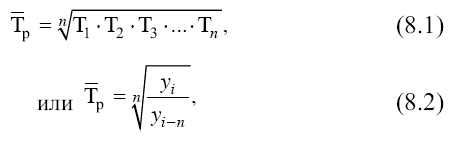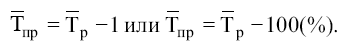Что такое динамика развития
динамика развития
Смотреть что такое «динамика развития» в других словарях:
ДИНАМИКА КУЛЬТУРЫ — (или культурная динамика) 1) изменения внутри культуры и во взаимодействии разных культур, для к рых характерна целостность, наличие упорядоченных тенденций, а также направленный характер; 2) раздел теории культуры, в рамках к… … Энциклопедия культурологии
ДИНАМИКА — (греч., от dynamis сила). 1) часть механики, имеющая предметом своим законы движения тел. 2) учение об изменяемости какого нибудь явления под влиянием тех или других сил; противоп. статике. Словарь иностранных слов, вошедших в состав русского… … Словарь иностранных слов русского языка
Динамика психопатий — является самым сложным и важным разделом учения о психопатиях. Лишь в динамике удается выявить степень выраженности симптома, характерные черты его становления, редукции и связь с другими патологическими образованиями. П. Б. Ганнушкин выделял… … Энциклопедический словарь по психологии и педагогике
динамика групповая — 1. Совокупность внутригрупповых социально психологических процессов и явлений, характеризующих весь цикл жизнедеятельности группы малой и его этапы: образование, функционирование, развитие, стагнацию, регресс, распад. К процессам динамики … Большая психологическая энциклопедия
ДИНАМИКА РАЗРЕЖЕННЫХ ГАЗОВ — раздел газовой динамики, в к ром при изучении течения газа низкой плотности учитывается его дискретная мол. структура. Методы Д. р. г., основанные на молекулярно кинетич. теории газов, применяются для определения теплового и силового воздействия… … Физическая энциклопедия
ДИНАМИКА — ДИНАМИКА, и, жен. 1. Раздел механики, изучающий движение тел под действием приложенных к ним сил. 2. Ход развития, изменения какого н. явления (книжн.). Д. общественного развития. 3. Движение, действие, развитие. В пьесе много динамики. | прил.… … Толковый словарь Ожегова
ДИНАМИКА — ДИНАМИКА, динамики, мн. нет, жен. (от греч. dynamikos действующий). 1. Отдел механики, изучающий законы движения тел в зависимости от действующих на них сил (мех.). 2. Ход развития, изменения какого нибудь явления под влиянием действующих на него … Толковый словарь Ушакова
ДИНАМИКА И СТАТИКА СОЦИАЛЬНЫЕ — введённые О. Контом понятия, обозначавшие различный подход к изучению обществ. явлений. Социальная динамика осн. внимание уделяла изучению процесса изменений социальных явлений, его обусловленности, направленности и последствий. В её… … Философская энциклопедия
ДИНАМИКА СОЦИАЛЬНАЯ — англ. dynamics, social; нем. Dynamik, soziale. 1. По О. Конту изучение структур соц. изменений. 2. Процесс непрерывного воспроизводства и развития соц. систем в отличие от соц. статики. Antinazi. Энциклопедия социологии, 2009 … Энциклопедия социологии
Динамика веры — «ДИНАМИКА ВЕРЫ» произведение немецко американского теолога, философа Пауля Тиллиха (Tillich P. Dynamics of faith. N. Y, 1957; рус. пер.: М., 1995). По степени значимости и влияния на умы оно стоит в одном ряду с такими известнейшими… … Энциклопедия эпистемологии и философии науки
Словари
Раздел механики, изучающий движение тел под воздействием приложенных к ним сил.
1. Движение, действие, развитие.
2. Состояние движения, ход развития какого-либо явления или процесса.
Морфология: (нет) чего? дина́мики, чему? дина́мике, (вижу) что? дина́мику, чем? дина́микой, о чём? о дина́мике
Курс динамики. | Динамика твёрдого тела.
2. Динамикой называют изменение, движение или развитие какого-либо процесса, явления, состояния и т. п.
Динамика экономического роста. | Оценить динамику общественного мнения. | Наблюдать динамику болезни.
3. Динамикой в произведении искусства называют насыщенность действием, внутренним движением.
Следить за динамикой событий в пьесе. | Его образы статичны, да и какая может быть динамика в повествовании о Вечном?
4. Динамикой песни, стиха и т. п. является сила, энергия их звучания.
Динамика стихотворения во многом определяется ритмом и размером.
1. Отдел механики, изучающий законы движения тел в зависимости от действующих на них сил (мех.).
2. Ход развития, изменения какого-нибудь явления под влиянием действующих на него сил; ант. статика во 2 знач. (научн.). Динамика социального процесса.
3. перен. Обилие движения, действия (книжн.). В пьесе много динамики.
1. Раздел механики, изучающий движение тел под действием приложенных к ним сил.
2. Ход развития, изменения какого-н. явления (книжн.). Д. общественного развития.
3. Движение, действие, развитие. В пьесе много динамики.
1) Раздел механики, изучающий движение тел под действием приложенных к ним сил.
2) книжн. Состояние движения, ход развития какого-л. явления.
Динамика численности животных.
Динамика роста инфляции.
3) перен. Движение, действие, развитие.
Видеть жизнь в динамике.
Мы вечно наталкиваемся на статику мысли, динамики же мысли не видно (Бердяев).
динами́ческий, динами́чный, аэродина́мика
Из западноевропейских языков (← греч. dynamis ‘сила’, ‘способность’).
Процесс движения, развития чего-л. и перспективы его развития;
Динамика исторических событий.
Раздел механики, изучающий законы движения тел под действием приложенных к ним сил.
Заведующий кафедрой механики был отличным специалистом в динамике.
1. Раздел механики, изучающий движение тел под действием приложенных к ним сил. Курс динамики.
2. Состояние чего-л., находящегося в движении, развитии, и перспективы его изменения (противоп.: ста́тика). Д. государственного бюджета. Д. производительности труда. Д. исторических событий. // Ход развития, движения чего-л. Д. сюжета пьесы. Д. стиха. Описать события в динамике.
3. Муз. Сила, энергия звучания.
◁ Динами́ческий; Динами́чный (см.).
1. Раздел механики, изучающий законы движения тел в зависимости от действующих на них сил.
2. Состояние движения, ход развития, изменения чего-л.
Динамика государственного бюджета. Динамика производительности труда. Динамика исторических событий.
Движение, действие, развитие.
Отсутствие динамики в романе.
3. муз. Сила звучания.
СТАТИКА И РАВНОВЕСИЕ
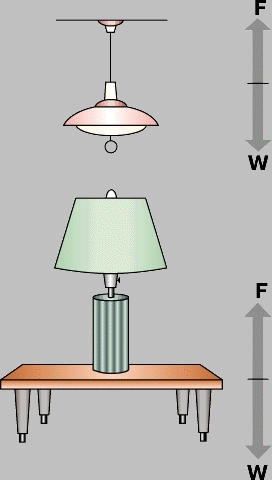
Равновесие. Тело, находящееся в состоянии покоя или равномерного и прямолинейного движения, находится в равновесии. Равнодействующая всех сил, действующих на такое тело, равна нулю. Если на тело, находящееся в равновесии, действуют только две силы, то они должны быть равны по величине и противоположны по направлению, так как только в этом случае их равнодействующая равна нулю. На рис. 1 показаны два примера тела, находящегося в равновесии в условиях, когда на него действуют две силы: лампа, стоящая на столе, и лампа, висящая на потолке. На настольную лампу действуют направленная вниз сила тяжести W, т.е. ее вес, и направленная вверх сила сопротивления стола F. Поскольку лампа находится в состоянии покоя, сила F должна быть равна по величине и противоположна по направлению силе W. Точно так же в случае висящей лампы тянущая вниз сила W должна быть равна по величине и противоположна по направлению тянущей вверх силе F натяжения шнура, на котором она подвешена.
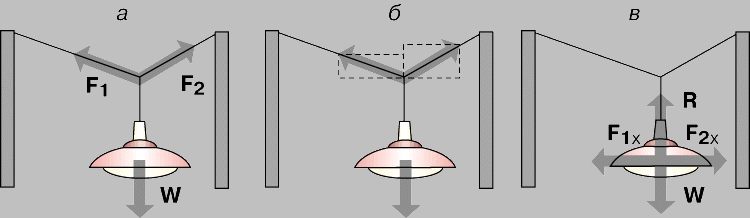
Разложение сил. Когда число сил, действующих на тело, находящееся в равновесии, больше двух, анализ несколько усложняется.
Равновесие и вращение. Во всех рассмотренных примерах равновесия действующие силы не только были равны по величине и противоположны по направлению, но и лежали на одной прямой или проходили через одну точку. Если же на твердое тело действуют силы, которые нельзя свести к одной, то они заставляют тело вращаться. (Две параллельные силы, равные по величине и противоположно направленные, называются парой сил.) Для того чтобы тело в таких условиях было в равновесии, т.е. не вращалось, пара сил должна быть уравновешена двумя такими же силами, вращающими тело в другую сторону.
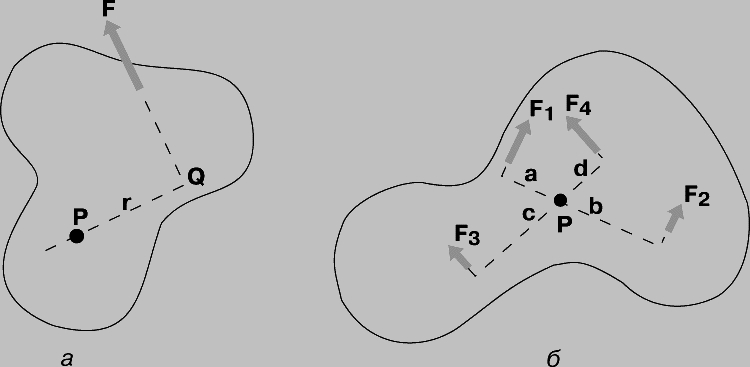
Момент силы. Если твердое тело закреплено в одной точке на шарнире и на него действует лишь одна сила, заставляющая его вращаться вокруг этой точки, то говорят, что тело вращается под действием момента силы. Момент силы равен произведению силы на ее плечо, т.е. на расстояние по перпендикуляру от точки закрепления до линии действия силы (рис. 4,а). Если на твердое тело действуют несколько сил, то тело не будет вращаться только при условии, что сумма моментов всех сил равна нулю (рис. 4,б).
Рис. 4. МОМЕНТ СИЛЫ равен произведению силы F (рис. 4,а) на плечо силы, т.е. на расстояние (по перпендикуляру) PQ от точки P шарнирного закрепления тела до линии действия силы F. В случае нескольких сил, действующих на твердое тело, способное вращаться вокруг точки P (рис. 4,б), условием равновесия является равенство нулю суммы моментов всех сил:
Равномерное движение. Тело движется равномерно, если в любую единицу времени своего движения оно проходит одно и то же расстояние в одном и том же направлении. Примером прямолинейного равномерного движения может служить движение космического аппарата, летящего по инерции в межзвездном пространстве достаточно далеко от всех небесных тел, там, где гравитационные поля ничтожно малы. Коль скоро на него не действуют никакие внешние силы, он будет, не останавливаясь, двигаться по прямой линии с постоянной скоростью. Но как только космический аппарат приблизится к какому-либо небесному телу, он окажется в гравитационном поле этого тела и начнет с нарастающей скоростью отклоняться к нему от прямолинейной траектории. Если же в межзвездном пространстве он войдет в плотное облако космической пыли, то (если отвлечься от гравитационного воздействия пыли) он по-прежнему будет двигаться прямолинейно, но с замедлением. В обоих случаях изменение характера движения вызывается действием неуравновешенных внешних сил.
Динамика изучает тела, находящиеся под воздействием неуравновешенных внешних сил, т.е. тела, характер движения которых изменяется. Поскольку равновесие означает равенство нулю равнодействующей всех сил, приложенных к телу, динамика, очевидно, имеет дело с силами, равнодействующая которых не равна нулю. Английский физик и математик И. Ньютон (1643-1727) сформулировал три закона движения, которым подчиняются тела, движущиеся под действием неуравновешенных сил, и за этими законами навсегда закрепилось его имя.
Первый закон Ньютона. Всякое тело сохраняет свое состояние покоя или равномерного и прямолинейного движения, пока неуравновешенные внешние силы не заставят его изменить это состояние. Поскольку состояние покоя, как и состояние равномерного и прямолинейного движения, соответствует равновесию, из первого закона Ньютона следует, что тело, находящееся в равновесии, остается в равновесии, пока его не выведут из этого состояния внешние силы.
Импульс (количество движения). Количеством движения тела называется произведение его массы m на его скорость v, т.е. величина mv. Количество движения одинаково у автомобиля массой 1 т, мчащегося со скоростью 100 км/ч, и у 2-тонного грузовика, едущего в том же направлении со скоростью 50 км/ч. Поскольку ускорение есть изменение скорости за малое время t, второй закон Ньютона можно переписать в виде mv = Ft. Произведение силы F на (малое) время ее действия t ранее называлось импульсом силы. Поэтому количество движения в настоящее время называют импульсом. Для импульса (количества движения) справедлив закон сохранения: при столкновении двух или нескольких тел их полный (суммарный) импульс не изменяется. Например, при забивании гвоздя молотком полный импульс молотка и гвоздя после удара равен полному импульсу молотка до удара (поскольку импульс гвоздя до удара был равен нулю).
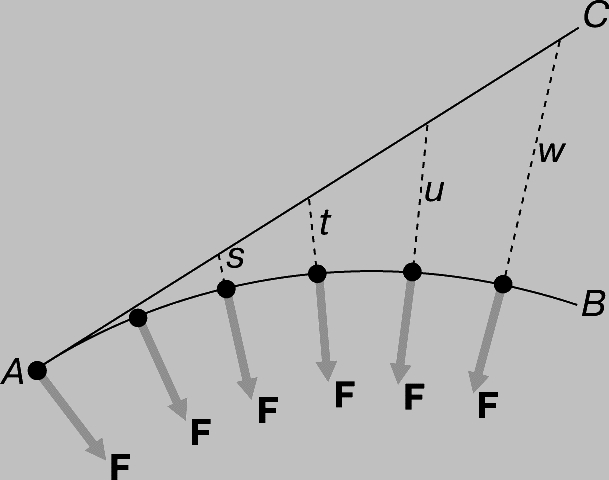
Рис. 6. УСКОРЕНИЕ, приобретаемое телом при движении по окружности. Двигаясь под действием центростремительной силы F по кривой AB, тело все больше удаляется от прямой AC (увеличиваются отклонения s, t, u, w).
Халфмэн Р. Динамика. М., 1972 Татаринов Я.В. Лекции по классической динамике. М., 1984 Ньютон И. Определения. Аксиомы и законы движения. М., 1985 Бабенков И.С. Основы статики и сопротивления материалов. М., 1988
дина́мика, дина́мики, дина́мик, дина́мике, дина́микам, дина́мику, дина́микой, дина́микою, дина́миками, дина́миках
Динамика
Содержание
Содержание
1. Динамика в разных науках
2. Динамика в физике
4. Газовая динамика
Динамика – это состояние движения, ход развития, изменение какого-либо явления под влиянием действующих на него факторов.
Динамика в разных науках
В физике
В астрономии
В науках о Земле
Динамика подземных вод
Динамика русловых потоков
В биологии
Популяционная динамика старения
Динамика растительности (синдинамика) — процесс постепенной трансформации растительных сообществ под действием внешних и внутренних факторов.
В технике
Динамика машин и механизмов
В музыке
Динамика в музыке — совокупность понятий и нотных обозначений, связанных с оттенками громкости звучания.
Динамика в физике
Динамика (греч. δύναμις — сила) — раздел механики, в котором изучаются причины возникновения механического движения. Динамика оперирует такими понятиями, как масса, сила, импульс, энергия.
Динамика, базирующаяся на законах Ньютона, называется классической динамикой. Классическая динамика описывает движения объектов со скоростями от долей миллиметров в секунду до километров в секунду.
Однако эти методы перестают быть справедливыми для движения объектов очень малых размеров (элементарные частицы) и при движениях со скоростями, близкими к скорости света. Такие движения подчиняются другим законам.
С помощью законов динамики изучается также движение сплошной среды, т. е. упруго и пластически деформируемых тел, жидкостей и газов.
В результате применения методов динамики к изучению движения конкретных объектов возник ряд специальных дисциплин: небесная механика, баллистика, динамика корабля, самолёта и т. п.
Основная задача динамики
Прямая задача динамики: по заданным силам определить характер движения тела.
Обратная задача динамики: по заданному характеру движения определить действующие на тело силы.
Классическая динамика основана на трёх основных законах Ньютона:
1-й: Существуют такие системы отсчета, относительно которых поступательно движущееся тело сохраняет свою скорость постоянной, если на него не действуют другие тела или их действие скомпенсировано.
2-й: В инерциальной системе отсчета сумма всех сил, действующих на тело, равна произведению массы этого тела на векторное ускорение этого же тела (действие на тело силы, проявляется в сообщении ему ускорения).
3-й: Тела действуют друг на друга силами равными по модулю и противоположными по направлению
Если при этом рассматриваются взаимодействующие материальные точки, то обе эти силы действуют вдоль прямой, их соединяющей. Это приводит к тому, что суммарный момент импульса системы состоящей из двух материальных точек в процессе взаимодействия остается неизменным. Таким образом, из второго и третьего законов Ньютона могут быть получены законы сохранения импульса и момента импульса
Законы Ньютона в неинерциальных системах отсчета
Существование инерциальных систем отсчета лишь постулируется первым законом Ньютона. Реальные системы отсчета, связанные, например, с Землей или с Солнцем, не обладают в полной мере свойством инерциальности в силу их кругового движения. Вообще говоря, экспериментально доказать существование ИСО невозможно, поскольку для этого необходимо наличие свободного тела (тела на которое не действуют никакие силы), а то, что тело является свободным, может быть показано лишь в ИСО. Описание же движения в неинерциальных системах отсчета, движущихся с ускорением относительно инерциальных, требует введения т. н. фиктивных сил таких как сила инерции, центробежная сила или сила Кориолиса.
Ряды динамики
Ряды динамики, статистические ряды, характеризующие изменение (развитие) социально-экономических явлений во времени. Например, данные о производстве электричества в СССР за период 1928—73 представляют Ряды динамики
Производство электричества в СССР, млрд. кетЧч
Последовательно расположенные во времени статистические данные называются уровнями Ряды динамики Они должны быть сопоставимы между собой, особенно в территориальном разрезе, по кругу охватываемых объектов, методике расчёта, критической дате, структуре. Уровни Ряды динамики могут характеризовать величину явлении за некоторые отрезки времени (интегральные Ряды динамики) или на определённую дату (моментные Ряды динамики). Анализ Ряды динамики состоит в определении скорости и интенсивности развития рассматриваемого явления, нахождении основные тенденции его развития (тренда), измерении колеблемости уровней, установлении связи с развитием др. явлений, проведении сравнительного анализа развития разных стран или районов. Для анализа Ряды динамики определяются статистические показатели: абсолютные приросты, темпы роста и прироста, средние уровни ряда, средние абсолютные приросты, средние темпы роста и прироста. Абсолютным приростом называют разность между последующим и предыдущим уровнями, а темпом роста — их отношение. Темп прироста составит разность между темпом роста и 1 (в коэффициенте) или 100%. Средний уровень ряда для интервальных рядов определяется как средняя арифметическая, а для моментных рядов — по формуле:
где — средний уровень, y1. — начальный, а уп — конечный, n — число уровней. Средний абсолютный прирост определяется как частное от деления абсолютного прироста за весь период на число единиц времени в периоде. Средний темп роста вычисляется как средняя геометрическая темпов роста за отдельные отрезки времени или как корень, степень которого определяется числом периодов, а под корнем берётся темп роста за весь период.
Определение тренда ведётся выравниванием статистическим. Колеблемость уровней Ряды динамики измеряется средней из квадратов отклонений фактических уровней от тренда. Для установления связи развития данного явления с другими пользуются методом корреляции Ряды динамики, отличающимся от обычного возможностью автокорреляции, авторегрессии, переменной корреляции и временного лага. Для сравнительного анализа разных стран (районов) часто используется приведение к одному основанию, состоящее в определении темпов роста для двух или более стран за одинаковые отрезки времени. Сравнительный анализ развития лучше вести с расчётом показателей на душу населения. Всесторонний анализ Ряды динамики позволяет выявить закономерности развития отражаемых в них явлений.
Газовая динамика
Газовая динамика, раздел гидро-аэромеханики, в котором изучается движение сжимаемых газообразных и жидких сред и их взаимодействие с твёрдыми телами. Как часть физики, Газовая динамика связана с термодинамикой и акустикой.
Фундаментальную роль в формировании Газовая динамика как самостоятельной науки сыграла опубликована в 1902 работа С. А. Чаплыгина «О газовых струях». Развитые в ней методы решения газодинамических задач получили впоследствии широкое распространение и обобщение. Плодотворный метод решения задач Газовая динамика предложили в 1908 нем. учёные Л. Прандтль и Т. Майер, исследовавшие частный случай течения газа с непрерывным увеличением скорости. В 1922 в работе «Опыт гидромеханики сжимаемой жидкости» советский учёный А. А. Фридман заложил основы динамической метеорологии. В 1929 нем. учёными Л. Прандтлем и А. Буземаном был разработан эффективный численно-графический метод решения широкого класса газодинамических задач, распространённый в 1934 сов. учёным Ф. И. Франклем на более сложные случаи течения газа. Эти методы широко применяются при решении задач Газовая динамика с помощью ЭВМ. В 1921 в СССР была создана, а в 1927 оформилась как научное учреждение газодинамическая лаборатория, деятельность которой совместно с Группой изучения реактивного движения (1932) заложила основы сов. ракетной техники.
Задачи газовой динамики при проектировании разнообразных аппаратов, двигателей и газовых машин состоят в определении сил давления и трения, температуры и теплового потока в любой точке поверхности тела или канала, омываемых газом, в любой момент времени. При исследовании распространения газовых струй, взрывных и ударных волн, горения и детонации методами Газовая динамика определяются давление, температура и др. параметры газа во всей области распространения. Изучение поставленных техникой сложных задач превратило современную газовою динамику в науку о движении произвольных смесей газов, которые могут содержать также твёрдые и жидкие частицы (например, выхлопные газы ракетных двигателей на жидком или твёрдом топливе), причём параметры, характеризующие состояние этих газов (давление, температура, плотность, электропроводность и др.), могут изменяться в широких пределах.
Для развития совресенной газовой динамики характерно неразрывное сочетание теоретических методов, использования ЭВМ и постановки сложных аэродинамических и физических экспериментов. Теоретические представления, частично опирающиеся на экспериментальные данные, позволяют описать с помощью уравнений движение газовых смесей сложного состава, в том числе многофазных смесей при наличии физико-химических превращений. Методами прикладной математики разрабатываются эффективные способы решения этих уравнений на ЭВМ. Наконец, из экспериментальных данных определяются необходимые значения физических и химических характеристик, свойственных изучаемой среде и рассматриваемым процессам (коэффициент вязкости и теплопроводности, скорости химических реакций, времена релаксации и др.).
Многие задачи, поставленные современной техникой перед газовой динамикой, пока не могут быть решены расчётно-теоретическими методами, в этих случаях широко пользуются газодинамическими экспериментами, поставленными на основе подобия теории и законов гидродинамического и аэродинамического моделирования. Газодинамические эксперименты в аэрогазодинамических лабораториях проводятся в сверхзвуковых и гиперзвуковых аэродинамических трубах, на баллистических установках, в ударных и импульсных трубах и на др. газодинамических установках специального назначения.
Газодинамические исследования ведутся в тех же научных учреждениях, что и исследования по аэродинамике, а результаты их публикуются в тех же научных журналах и сборниках.
Анализ динамики
Динамика социально-экономических явлений и задачи ее статистического изучения
Явления общественной жизни, изучаемые социально-экономической статистикой, находятся в непрерывном изменении и развитии. С течением времени – от месяца к месяцу, от года к году – изменяются численность населения и его состав, объем производимой продукции, уровень производительности труда и т. д., поэтому одной из важнейших задач статистики является изучение изменения общественных явлений во времени – процесса их развития, их динамики. Эту задачу статистика решает путем построения и анализа рядов динамики (временных рядов).
Ряд динамики (хронологический, динамический, временной ряд) – это последовательность упорядоченных во времени числовых показателей, характеризующих уровень развития изучаемого явления. Ряд включает два обязательных элемента: время и конкретное значение показателя (уровень ряда).
Каждое числовое значение показателя, характеризующее величину, размер явления, называется уровнем ряда. Кроме уровней каждый ряд динамики содержит указания о тех моментах либо периодах времени, к которым относятся уровни.
При подведении итогов статистического наблюдения получают абсолютные показатели двух видов. Одни из них характеризуют состояние явления на определенный момент времени: наличие на этот момент каких-либо единиц совокупности или наличие того или иного объема признака. К таким показателям относится численность населения, парк автомобилей, жилищный фонд, товарные запасы и т. д. Величину таких показателей можно определить непосредственно только по состоянию на тот или иной момент времени, а потому эти показатели и соответствующие ряды динамики и называются моментными.
Другие показатели характеризуют итоги какого-либо процесса за определенный период (интервал) времени (сутки, месяц, квартал, год и т. п.). Такими показателями являются, например, число родившихся, количество произведенной продукции, ввод в действие жилых домов, фонд заработной платы и др. Величину этих показателей можно подсчитать только за какой-нибудь интервал (период) времени, поэтому такие показатели и ряды их значений называются интервальными.
Из различного характера интервальных и моментных абсолютных показателей вытекают некоторые особенности (свойства) уровней соответствующих рядов динамики. В интервальном ряду величина уровня, представляющего собой итог какого-либо процесса за определенный интервал (период) времени, зависит от продолжительности этого периода (длины интервала). При прочих равных условиях уровень интервального ряда тем больше, чем больше длина интервала, к которому этот уровень относится.
В моментных же рядах динамики, где тоже есть интервалы – промежутки времени между соседними в ряду датами, – величина того или иного конкретного уровня не зависит от продолжительности периода между соседними датами.
Каждый уровень интервального ряда уже представляет собой сумму уровней за более короткие промежутки времени. При этом единица совокупности, входящая в состав одного уровня, не входит в состав других уровней, поэтому в интервальном ряду динамики уровни за примыкающие друг к другу периоды времени можно суммировать, получая итоги (уровни) за более продолжительные периоды (так, суммируя месячные уровни, получим квартальные, суммируя квартальные, получим годовые, суммируя годовые – многолетние).
Иногда путем последовательного сложения уровней интервального ряда за примыкающие друг к другу интервалы времени строится ряд нарастающих итогов, в котором каждый уровень представляет собой итог не только за данный период, но и за другие периоды, начиная с определенной даты (с начала года и т. д.). Такие нарастающие итоги нередко приводятся в бухгалтерских и других отчетах предприятий.
В моментном динамическом ряду одни и те же единицы совокупности обычно входят в состав нескольких уровней, поэтому суммирование уровней моментного ряда динамики само по себе не имеет смысла, так как получающиеся при этом итоги лишены самостоятельной экономической значимости.
Выше говорилось о рядах динамики абсолютных величин, являющихся исходными, первичными. Наряду с ними могут быть построены ряды динамики, уровни которых являются относительными и средними величинами. Они также могут быть либо моментными, либо интервальными. В интервальных рядах динамики относительных и средних величин непосредственное суммирование уровней само по себе лишено смысла, так как относительные и средние величины являются производными и исчисляются путем деления других величин.
При построении и перед анализом ряда динамики нужно прежде всего обратить внимание на то, чтобы уровни ряда были сопоставимы между собой, так как только в этом случае динамический ряд будет правильно отражать процесс развития явления. Сопоставимость уровней ряда динамики – это важнейшее условие обоснованности и правильности выводов, полученных в результате анализа этого ряда. При построении динамического ряда надо иметь в виду, что ряд может охватывать большой период времени, в течение которого могли произойти изменения, нарушающие сопоставимость (территориальные изменения, изменения круга охвата объектов, методологии расчетов и т. д.).
При изучении динамики общественных явлений статистика решает следующие задачи:
Основные показатели рядов динамики
При изучении динамики используются различные показатели и методы анализа, как элементарные, более простые, так и более сложные, требующие соответственно применения более сложных разделов математики.
Простейшими показателями анализа, которые используются при решении ряда задач, в первую очередь при измерении скорости изменения уровня ряда динамики, являются абсолютный прирост, темпы роста и прироста, а также абсолютное значение (содержание) одного процента прироста. Расчет этих показателей основан на сравнении между собой уровней ряда динамики. При этом уровень, с которым производится сравнение, называется базисным, так как он является базой сравнения. Обычно за базу сравнения принимается либо предыдущий, либо какой-либо предшествующий уровень, например первый уровень ряда.
Если каждый уровень сравнивается с предыдущим, то полученные при этом показатели называются цепными, так как они представляют собой как бы звенья «цепи», связывающей между собой уровни ряда. Если же все уровни связываются с одним и тем же уровнем, выступающим как постоянная база сравнения, то полученные при этом показатели называются базисными.
Часто построение ряда динамики начинают с того уровня, который будет использован в качестве постоянной базы сравнения. Выбор этой базы должен быть обоснован историческими и социально-экономическими особенностями развития изучаемого явления. В качестве базисного целесообразно брать какой-либо характерный, типичный уровень, например конечный уровень предыдущего этапа развития (или средний его уровень, если на предыдущем этапе уровень то повышался, то понижался).
Абсолютный прирост показывает, на сколько единиц увеличился (или уменьшился) уровень по сравнению с базисным, т. е. за тот или иной промежуток (период) времени. Абсолютный прирост равен разности между сравниваемыми уровнями и измеряется в тех же единицах, что и эти уровни:
где уi – уровень i-го года; yi-1 – уровень предшествующего года; y0 – уровень базисного года. Если уровень уменьшился по сравнению с базисным, то ? ‹ 0; он характеризует абсолютное уменьшение уровня.
Абсолютный прирост за единицу времени (месяц, год) измеряет абсолютную скорость роста (или снижения) уровня. Цепные и базисные абсолютные приросты связаны между собой: сумма последовательных цепных приростов равна соответствующему базисному приросту, т. е. общему приросту за весь период.
Более полную характеристику роста можно получить только тогда, когда абсолютные величины дополняются относительными. Относительными показателями динамики являются темпы роста и темпы прироста, характеризующие интенсивность процесса роста.
Темп роста (Тр) – статистический показатель, который отражает интенсивность изменения уровней ряда динамики и показывает, во сколько раз увеличился уровень по сравнению с базисным, а в случае уменьшения – какую часть базисного уровня составляет сравниваемый уровень; измеряется отношением текущего уровня к предыдущему или базисному:
Как и другие относительные величины, темп роста может быть выражен не только в форме коэффициента (простого отношения уровней), но и в процентах. Как и абсолютные приросты, темпы роста для любых рядов динамики сами по себе являются интервальными показателями, т. е. характеризуют тот или иной промежуток (интервал) времени.
Между цепными и базисными темпами роста, выраженными в форме коэффициентов, существует определенная взаимосвязь: произведение последовательных цепных темпов роста равно базисному темпу роста за весь соответствующий период, например: y2/ y1 y3/ y2 = y3/ y1.
Темп прироста (Тпр) характеризует относительную величину прироста, т. е. представляет собой отношение абсолютного прироста к предыдущему или базисному уровню:
Темп прироста, выраженный в процентах, показывает, на сколько процентов увеличился (или уменьшился) уровень по сравнению с базисным, принятым за 100 %.
При анализе темпов развития никогда не следует упускать из виду, какие абсолютные величины – уровни и абсолютные приросты – скрываются за темпами роста и прироста. Нужно, в частности, иметь в виду, что при снижении (замедлении) темпов роста и прироста абсолютный прирост может возрастать.
В связи с этим важно изучать еще один показатель динамики – абсолютное значение (содержание) 1 % прироста, который определяется как результат деления абсолютного прироста на соответствующий темп прироста:
Эта величина показывает, сколько в абсолютном выражении дает каждый процент прироста. Иногда уровни явления за одни годы несопоставимы с уровнями за другие годы из-за территориальных, ведомственных и иных изменений (изменения методологии учета и исчисления показателей и т. п.). Чтобы обеспечить сопоставимость и получить пригодный для анализа временной ряд, нужно произвести прямой пересчет уровней, несопоставимых с другими. Однако иногда нет необходимых для этого данных. В таких случаях можно использовать особый прием, называемый смыканием рядов динамики.
Пусть, например, произошло изменение границ территории, по которой изучалась динамика развития какого-то явления в i-м году. Тогда данные, полученные до этого года, окажутся несопоставимы с данными за последующие годы. Чтобы сомкнуть эти ряды и получить возможность анализа динамики ряда за весь период, примем в каждом из них за базу сравнения уровень i-го года, за который есть данные как в прежних, так и в новых границах территории. Эти два ряда с одинаковой базой сравнения можно затем заменить одним сомкнутым рядом динамики. По данным сомкнутого ряда можно вычислить темпы роста по сравнению с любым годом, можно рассчитать и абсолютные уровни за весь период в новых границах. Тем не менее надо иметь в виду, что результаты, полученные путем смыкания рядов динамики, содержат в себе некоторую погрешность.
Графически динамика явлений наиболее часто изображается в виде столбиковых и линейных диаграмм. Применяются и другие формы диаграмм: фигурные, квадратные, секторные и т. п. Аналитические графики обычно строятся в виде линейных диаграмм.
Средние показатели динамики
С течением времени изменяются не только уровни явлений, но и показатели их динамики – абсолютные приросты и темпы развития, поэтому для обобщающей характеристики развития, для выявления и измерения типичных основных тенденций и закономерностей и решения других задач анализа используются средние показатели временного ряда – средние уровни, средние абсолютные приросты и средние темпы динамики.
К расчету средних уровней ряда динамики часто приходится прибегать уже при построении временного ряда – для обеспечения сопоставимости числителя и знаменателя при расчете средних и относительных величин. Пусть, например, нужно построить ряд динамики производства электроэнергии на душу населения в Российской Федерации. Для этого за каждый год необходимо количество произведенной электроэнергии в данном году (интервальный показатель) разделить на численность населения в том же году (момент-ный показатель, величина которого непрерывно меняется на протяжении года). Ясно, что численность населения на тот или иной момент времени в общем случае несопоставима с объемом производства за весь год в целом. Для обеспечения сопоставимости нужно и численность населения как-то приурочить ко всему году, а это можно сделать, лишь рассчитав среднюю численность населения за год.
Часто приходится прибегать к средним показателям динамики и потому, что уровни многих явлений сильно колеблются от периода к периоду, например от года к году, то повышаясь, то понижаясь. Особенно это относится ко многим показателям сельского хозяйства, где год на год не приходится, поэтому при анализе развития сельского хозяйства чаще оперируют не годовыми показателями, а более типичными и устойчивыми среднегодовыми показателями за несколько лет.
При вычислении средних показателей динамики необходимо иметь в виду, что к этим средним показателям полностью относятся общие положения теории средних величин. Это означает прежде всего, что динамическая средняя будет типичной, если она характеризует период с однородными, более или менее стабильными условиями развития явления. Выделение таких периодов – этапов развития – в определенном отношении аналогично группировке. Если же динамическая средняя величина исчислена за период, в течение которого условия развития явления существенно менялись, т. е. период, охватывающий разные этапы развития явления, то такой средней величиной нужно пользоваться с большой осторожностью, дополняя ее средними величинами за отдельные этапы.
Средние показатели динамики должны также удовлетворять логико-математическому требованию, согласно которому при замене средней величиной тех фактических величин, из которых получена средняя, не должна изменяться величина определяющего показателя, т. е. некоторого обобщающего показателя, связанного с осредняемым показателем. Метод расчета среднего уровня ряда динамики зависит прежде всего от характера показателя, лежащего в основе ряда, т. е. от вида временного ряда.
Наиболее просто вычисляется средний уровень интервального ряда динамики абсолютных величин с равностоящими уровнями. Расчет производится по формуле простой средней арифметической:
где n – число фактических уровней за последовательные равные отрезки времени.
Сложнее обстоит дело с вычислением среднего уровня моментного ряда динамики абсолютных величин. Момент-ный показатель может изменяться почти непрерывно, поэтому чем более подробны и исчерпывающи данные о его изменении, тем более точно можно вычислить средний уровень. Более того, сам метод расчета зависит от того, насколько подробны имеющиеся данные. Здесь возможны различные случаи.
При наличии исчерпывающих данных об изменении мо-ментного показателя его средний уровень вычисляется по формуле средней арифметической взвешенной для интервального ряда с разностоящими уровнями:
где t – число периодов времени, в течение которых уровень не изменялся.
Если промежутки времени между соседними датами равны друг другу, т. е. когда мы имеем дело с равными (или примерно равными) интервалами между датами (например, когда известны уровни на начало каждого месяца или квартала, года), тогда для моментного ряда с равностоящими уровнями расчет среднего уровня ряда производим по формуле средней хронологической:
Для моментного ряда с разностоящими уровнями расчет среднего уровня ряда производится по формуле
Выше шла речь о среднем уровне рядов динамики абсолютных величин. Для рядов динамики средних и относительных величин средний уровень нужно вычислять исходя из содержания и смысла этих средних и относительных показателей.
Средний абсолютный прирост показывает, на сколько единиц увеличивался или уменьшался уровень по сравнению с предыдущим периодом в среднем за единицу времени (в среднем ежемесячно, ежегодно и т. д.). Средний абсолютный прирост характеризует среднюю абсолютную скорость роста (или снижения) уровня и всегда является интервальным показателем. Он вычисляется путем деления общего прироста за весь период на длину этого периода в тех или иных единицах времени:
где – цепные абсолютные приросты за последовательные промежутки времени; n – число цепных приростов; У0 – уровень базисного периода.
В качестве основы и критерия правильности исчисления среднего темпа роста (как и среднего абсолютного прироста) можно использовать в роли определяющего показателя произведение цепных темпов роста, которое равно темпу роста за весь рассматриваемый период. Таким образом, перемножив n цепных темпов роста, мы получим темп роста за весь период:
из которого следует:
где n – число уровней ряда динамики; Т1, Т2, Тп – цепные темпы роста.
Формула (8.1) носит название простой средней геометрической, (8.2) – средней геометрической в неявном виде.
Средний темп роста, выраженный в форме коэффициента, показывает, во сколько раз увеличивается уровень по сравнению с предыдущим периодом в среднем за единицу времени (в среднем ежегодно, ежемесячно и т. п.).
Для средних темпов роста и прироста сохраняет силу та же взаимосвязь, которая имеет место между обычными темпами роста и прироста:
Средний темп прироста (или снижения), выраженный в процентах, показывает, на сколько процентов увеличивался (или снижался) уровень по сравнению с предыдущим периодом в среднем за единицу времени (в среднем ежегодно, ежемесячно и т. п.). Средний темп прироста характеризует среднюю интенсивность роста, т. е. среднюю относительную скорость изменения уровня.
Из двух видов формулы среднего темпа роста чаще используется формула (8.2), так как она не требует вычисления всех цепных темпов роста. По формуле (8.1) расчет целесообразно производить лишь в тех случаях, когда неизвестны ни уровни ряда динамики, ни темп роста за весь период, а известны только цепные темпы роста (или прироста).
Выявление и характеристика основной тенденции развития
Одной из задач, возникающих при анализе рядов динамики, является установление закономерности изменения уровней изучаемого показателя во времени. Для этого необходимо выделить такие периоды (этапы) развития, которые достаточно однородны в отношении взаимосвязи данного явления с другими и условий его развития.
Выделение этапов развития – это задача, находящаяся на стыке науки, изучающей данное явление (экономики, социологии и т. п.), и статистики. Решение этой задачи осуществляется не только и даже не столько с помощью статистических методов (хотя и они могут принести определенную пользу), сколько на базе содержательного анализа сущности, природы явления и общих законов его развития.
Для каждого этапа развития нужно выявить и численно охарактеризовать основную тенденцию изменения уровня явления. Под тенденцией понимается общее направление к росту, снижению или стабилизации уровня явления с течением времени. Если уровень непрерывно растет или непрерывно снижается, то тенденция к росту или снижению наблюдается отчетливо: она легко обнаруживается визуально по графику временного ряда. Следует, однако, иметь в виду, что и рост, и снижение уровня могут происходить по-разному: либо равномерно, либо ускоренно, либо замедленно. Под равномерным ростом (или снижением) понимается рост (или снижение) с постоянной абсолютной скоростью, когда цепные абсолютные приросты (i) одинаковы. При ускоренном росте или снижении цепные приросты систематически увеличиваются по абсолютной величине, а при замедленном росте или снижении – уменьшаются (тоже по модулю). Практически уровни ряда динамики очень редко растут (или снижаются) строго равномерно. Нечасто встречается и систематическое, без единого отклонения, увеличение или снижение цепных приростов.
Такие отклонения объясняются либо изменением с течением времени всего комплекса основных причин и факторов, от которых зависит уровень явления, либо изменением направления и силы действия второстепенных, в том числе случайных, обстоятельств и факторов, поэтому при анализе динамики идет речь не просто о тенденции развития, а об основной тенденции, достаточно стабильной (устойчивой) на протяжении данного этапа развития. В некоторых случаях эта закономерность, общая тенденция развития объекта вполне четко отображаются уровнями динамического ряда.
Основной тенденцией (трендом) называется достаточно плавное и устойчивое изменение уровня явления во времени, более или менее свободное от случайных колебаний. Основную тенденцию можно представить либо аналитически – в виде уравнения (модели) тренда, либо графически. Выявление основной тенденции развития (тренда) называется в статистике также выравниваем временного ряда, а методы выявления основной тенденции – методами выравнивания.
Одними из самых распространенных способов выявления основных тенденций (тренда) ряда динамики являются методы:
1) f (t) = a0 + a1t – линейная зависимость;
2) f (t) = a0 + a1t + a2t 2 – параболическая зависимость. Способ укрупнения интервалов и их характеристики средними уровнями заключается в переходе от интервалов менее продолжительных к более продолжительным, например от суток – к неделям или декадам, от декад – к месяцам, от месяцев – к кварталам или годам, от годовых интервалов – к многолетним. Если уровни ряда динамики колеблются с более или менее определенной периодичностью (волнообразно), то укрупненный интервал целесообразно взять равным периоду колебаний (длине «волны» цикла). Если же такая периодичность отсутствует, то укрупнение производят постепенно от малых интервалов к все более крупным, пока общее направление тренда не станет достаточно отчетливым.
Если ряд динамики является моментным, а также в тех случаях, когда уровень ряда является относительной или средней величиной, суммирование уровней не имеет смысла, и следует охарактеризовать укрупненные периоды средними уровнями.
При укрупнении интервалов число членов динамического ряда сильно сокращается, в результате чего движение уровня внутри укрупненного интервала выпадает из поля зрения. В связи с этим для выявления основной тенденции и более детальной ее характеристики используется сглаживание ряда с помощью скользящей средней.
Сглаживание ряда динамики с помощью скользящей средней заключается в том, что вычисляется средний уровень из определенного числа первых по порядку уровней ряда, затем – средний уровень из такого же числа уровней, начиная со второго, далее, начиная с третьего и т. д. Таким образом, при расчетах среднего уровня как бы «скользят» по временному ряду от его начала к концу, каждый раз отбрасывая один уровень в начале и добавляя один следующий. Отсюда название – скользящая средняя.
Каждое звено скользящей средней – это средний уровень за соответствующий период. При графическом изображении и при некоторых расчетах каждое звено принято условно относить к центральному интервалу того периода, за который сделан расчет (для моментального ряда – к центральной дате).
Вопрос о том, за какой период следует вычислять звенья скользящей средней, решается в зависимости от конкретных особенностей динамики. Как и при укрупнении интервалов, если в колебаниях уровня есть определенная периодичность, то период сглаживания целесообразно принять равным периоду колебаний или кратной его величине. Так, при наличии квартальных уровней, испытывающих ежегодно сезонные спады и повышения, целесообразно применять четырех– или восьмиквартальную среднюю и т. п. Если же колебания уровней являются беспорядочными, то целесообразно постепенно укрупнять интервал сглаживания, пока не выявится отчетливая картина тренда.
Аналитическое выравнивание ряда динамики позволяет получить аналитическую модель тренда. Оно производится следующим образом.
Выбор формы кривой во многом определяет результаты экстраполяции тренда. Основанием для выбора вида кривой может использоваться содержательный анализ сущности развития данного явления. Можно опираться также на результаты предыдущих исследований в данной области. Наиболее простой эмпирический прием – визуальный: выбор формы тренда на основе графического изображения ряда – ломаной линии. На практике линейная зависимость используется чаще, чем параболическая, в силу ее простоты.