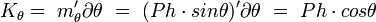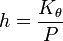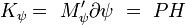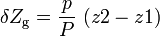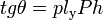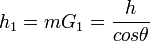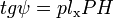Что такое динамическая остойчивость судна

Статическая и динамическая остойчивость.

Если кренящее усилие, воздействующее на судно, нарастает постепенно, то говорят о так называемой «статической остойчивости». В этом случае восстанавливающий момент сначала также плавно увеличивается с увеличением угла крена и смещением центра величины к борту, а затем начинает уменьшаться (см. диаграмму статической остойчивости). По достижении кренящим моментом какого-либо конечного значения судно остаётся в накренённом положении. Для примера, представим себе плавающую у причала лодку и человека, который, повиснув на причале на руках, постепенно переносит вес своего тела на борт лодки, или судно, которое грузят навалочным грузом при помощи транспортёра, постепенно насыпая груз к одному борту. Восстанавливающий момент, создаваемый силой, равной по величине водоизмещению судна, в процессе накренения постоянно оказывается равен кренящему. Поэтому, зная величину кренящего момента, угол крена можно определить по диаграмме статической остойчивости, разделив кренящий момент на водоизмещение судна и отложив на диаграмме получившееся плечо восстанавливающего момента.

Как видно из рис. 19, при накренении судна на больший, чем при статическом воздействии угол, восстанавливающий момент оказывается больше кренящего при нарастании крена до угла, соответствующего максимуму диаграммы статической остойчивости. При накренении на больший угол, кренящий момент становится больше опрокидывающего и судно переворачивается. Поэтому, как мы увидим в дальнейшем, при нормировании остойчивости используются как понятие «угла заката», так и понятие «угла максимума» диаграммы статической остойчивости. По этой же причине при расчётач угла крена с помощью диаграммы статической остойчивости используется только восходящая её ветвь.

Источник

Диаграмма динамической остойчивости

Судно при этом получает динамический угол крена, хотя и кратковременный, но значительно превышающий крен, который мог бы возникнуть при статическом действии этого же момента.

Представим, что к судну, находящемуся в нормальном (прямом) положении внезапно приложен кренящий момент Мкр, под действием которого судно начнет крениться с постоянно нарастающей скоростью (с ускорением), т. к. в начальный период восстанавливающий момент Мв будет нарастать значительно медленнее Мкр.
После достижения судном угла статического равновесия θст, т. е. когда Мкр = Мв, угловая скорость максимальна. Судно по инерции продолжает крениться, но уже с убывающей угловой скоростью (замедлением). Объясняется это тем, что Мв становится больше, чем Мкр.

В какой-то момент угловая скорость становится равной 0, накренение судна прекращается (судно «замрет» в нижней точке крена) и угол крена достигает своего максимума. Этот угол называется углом динамического крена θдин. Затем судно начнет возвращаться в первоначальное положение.

Динамической остойчивостью называют способность судна выдерживать динамическое воздействие кренящего момента.

Относительной мерой динамической остойчивости является плечо динамической остойчивости lдин.

Кривую, выражающую зависимость работы восстанавливающего момента или плеча динамической остойчивости от угла крена, называют диаграммой динамической остойчивости (ДДО).

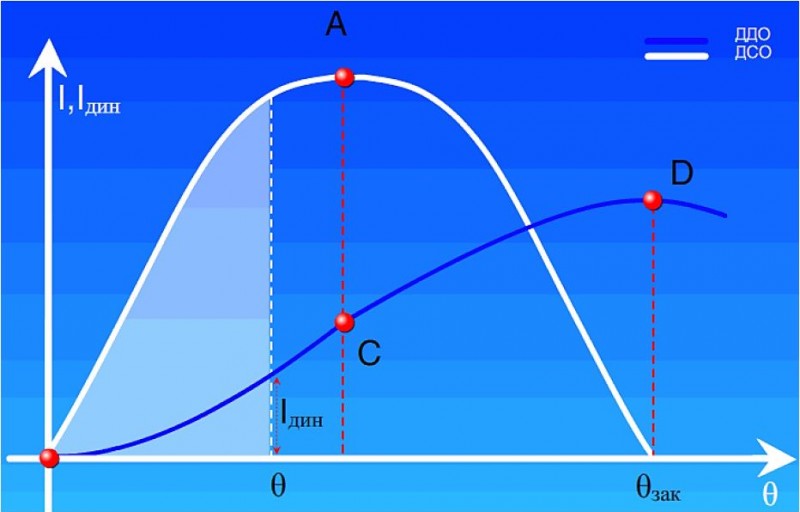
Графическое изображение диаграммы динамической остойчивости по отношению к диаграмме статической остойчивости дано на рис. 9.5., из которого видно, что:

точки пересечения диаграммы статической остойчивости с осью абсцисс отвечают точкам О и D экстремума диаграммы динамической остойчивости;

точка А максимума диаграммы статической остойчивости соответствует точке перегиба С диаграммы динамической остойчивости;

любая ордината диаграммы динамической остойчивости, отвечающая некоторому углу крена θ, представляет в масштабе соответствующую этому углу крена площадь диаграммы статической остойчивости (заштрихована на рисунке).

Диаграммы статической и динамической остойчивости

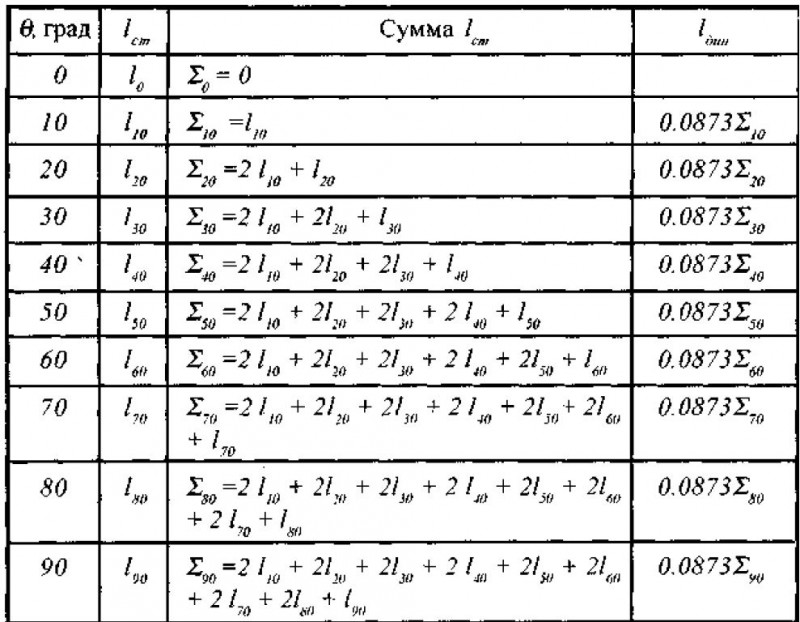
Обычно в судовых условиях строят диаграмму динамической остойчивости по известной диаграмме статической остойчивости, схема вычислений плеч динамической остойчивости приведена в табл:

Плечи динамической остойчивости

Диаграмма динамической остойчивости судна

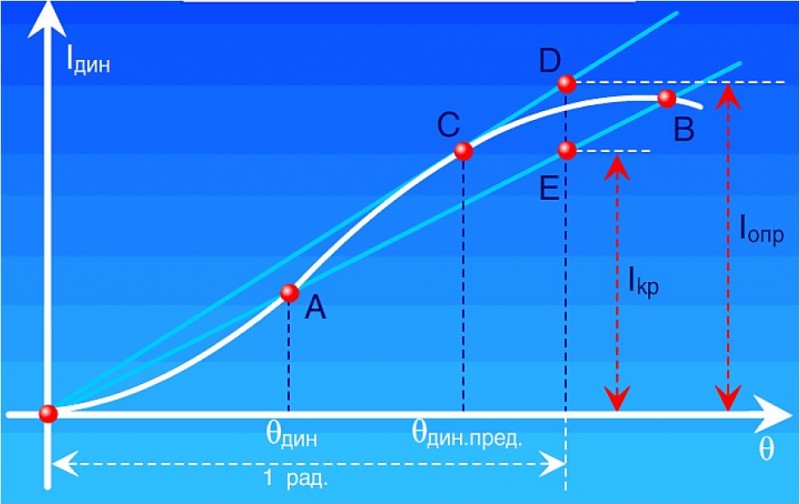
Точка В практического значения не имеет.

Если построенный таким образом график произведения lкр*θ вообще не пересекает диаграмму динамической остойчивости, то это означает, что судно опрокидывается.

Для нахождения опрокидывающего момента, который еще может выдержать судно не опрокидываясь, следует провести из начала координат касательную к диаграмме динамической остойчивости до пересечения ее в точке D с вертикалью, соответствующей крену в 1 радиан.
Отрезок этой вертикали от оси абсцисс до пересечения ее с касательной дает плечо опрокидывающего момента lопр, а сам момент определится умножением плеча lопр на силу веса судна Р. Точка касания С определит предельный угол динамического крена θдин.преп.

Источник

Динамическая остойчивость судна

В ряде случаев судоводителю приходится обращаться к вопросам динамической остойчивости судна. Конечно, в этих случаях судоводитель не решает сложных задач динамики судна – эта область деятельности ученных и исследователей в области теории судна. Но при решении отдельных задач, например при определении динамического крена, при определении предельных значений восстанавливающего момента, после которых судно опрокидывается, и при проверке соответствия параметров остойчивости принятым международным нормам без вопросов динамической остойчивости, хотя бы даже в упрощенной постановке, не обойтись.

Рассмотрение динамики наклонения судна в поперечной плоскости на этом уровне допустимо без учета инерции судна и потерь энергии на взаимодействие с жидкостью. В такой постановке достаточным оказывается использование понятия механической работы, совершаемой кренящим и восстанавливающим моментами, и сопоставлением их величин между собой.

Прежде чем перейти к специальным средствам теории динамической остойчивости, рассмотрим случай динамического накренения судна под действием ударной нагрузки от внезапного шквалистого ветра, пользуясь диаграммой статической остойчивости.

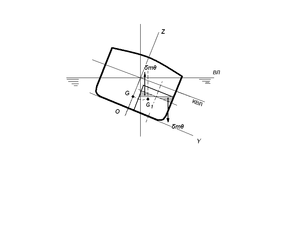
Предположим, что на плавающее без хода на поверхности спокойной воды судно внезапно обрушивается со стороны борта ветровой шквал. Этот шквал характеризуется возникновением ветровой нагрузки на надводной части судна и приводит к появлению внезапно действующего кренящего момента. Вид этого момента во времени представлены на Рисунке

Плечо кренящего момента от шквалистого ветра

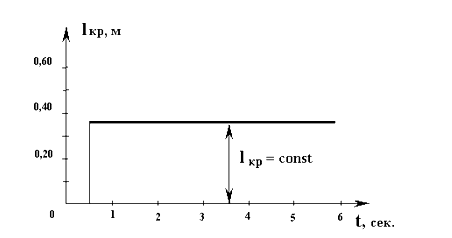
Можно с некоторой погрешностью считать, что величина этого кренящего момента слабо зависит от крена судна, т.е. считать его по крену постоянной величиной М_кр (θ) = const. Графическая зависимость такого кренящего момента, помещенная на диаграмму статической остойчивости, выглядит как горизонтальная линия с ординатой, равной величине этого момента (М_кр = М * _кр),

Крен судна от действия шквала

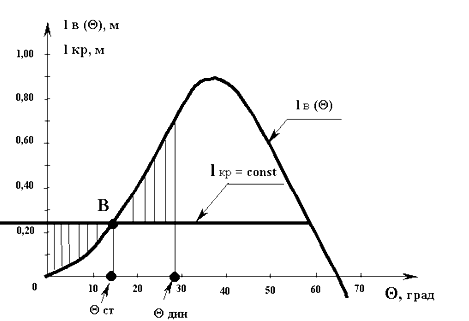
Теперь, если постараться проследить процесс наклонения судна на ДСО, от момента времени, когда восстанавливающий момент еще был равен нулю, то по мере развития (нарастания) угла крена судно будет разгоняться по угловой скорости вращения относительно продольной оси ОХ и приобретать инерцию. Дойдя на ДСО до точки пересечения обоих графиков (точка В на Рис. 9) судно не остановится и будет по инерции крениться дальше.

После точки В разница между обоими участвующими моментами становиться больше в пользу восстанавливающего момента (∆М = М_в – М_кр > 0), следовательно, этот результирующий момент будет совершать работу, пытаясь остановить его накренение. По-видимому, процесс динамического наклонения судна прекратится в момент времени, которому будет соответствовать равенство работ, совершенных каждым из моментов на своем пути.

Вспомним, что в механике работа при вращении тела вычисляется как произведение момента на угловой путь (в нашем случае это текущий угол крена судна). Для постоянного момента его работа вычисляется как произведение кренящего момента на угловой путь.

Для переменного по углу крена восстанавливающего момента работа вычисляется по общей формуле механики с использованием операции интегрирования переменного восстанавливающего момента по углу крена:

В судовых расчетах динамической остойчивости широко используется аналогия между величиной работы и площадью под графиком восстанавливающего момента. В данном рассмотренном случае удобно использовать подобную трактовку для нахождения момента окончания наклонения судна под действием шквала и соответствующий этому моменту динамический угол крена. Этот угол крена может быть найден на Рис. 9 путем взаимного подбора площадей под обоими графиками до их равенства.

Можно сделать вывод о том, что причиной больших динамических отклонений судна (это видно из сравнений крена θ_в и θ_g при одной и той же величине кренящего момента) является первоначальное «запаздывание» величины восстанавливающего момента, который нарастает постепенно от нуля, и его величина пока меньше величины кренящего момента. За это время, подходя к точке В, судно накапливает инерцию вращения, которую потом ему же самому приходится гасить с помощью увеличившегося к этому времени восстанавливающего момента. Результат этого процесса – значительно большие углы динамического крена по сравнению со статическим, либо даже опрокидывание судна.

Попутно здесь же можно сразу определить тот предельный кренящий динамический момент, действие которого судно уже удержать не сможет, обладая данной остойчивостью и ДСО.

Такой предельный момент называется опрокидывающим моментом (М_опр). Его значение находят на ДСО способом последовательных приближений, постепенно увеличивая величину кренящего момента (подбором более интенсивного шквала); наступает момент расчета, когда для площади под графиком кренящего момента М_кр (θ) уже не найдется равной по величине площади под графиком ДСО.

Как видно, решение задачи по нахождению опрокидывающего момента с помощью ДСО, сопряжено с необходимостью вычисления площадей и большим объемом вычислений. Для облегчения процедуры вычислений используется диаграмма динамической остойчивости (ДДО).

ДДО представляет собой графическую зависимость работы восстанавливающего момента от угла крена.

Такую диаграмму целесообразно построить заранее, сразу после построения ДСО, и использовать при решении динамических задач.

ДДО вычисляется на основе формулы (12), следовательно, график ДДО обладает свойствами интегральной кривой по отношению к графику подынтегральной функции, т.е. к ДСО. При углах крена θ = 0 и θ = θ₃, где М_в = 0, ДДО должна иметь экстремальные точки, т.е. минимум и максимум, соответственно, а при угле крена θ = θ_m, где М_в(θ) принимает максимальное значение – ДДО будет иметь точку перегиба. Важно отметить, что ДДО при всех вариантах остойчивости судна (при всех h₀) должна в начале координат иметь горизонтальную касательную.

Из прочих свойств ДДО можно отметить следующие:

так же будет возрастать угол заката, поскольку у соответствующих ДСО он увеличивается с ростом исходной МВ (h₀ испр ).

Диаграммы статической и динамической остойчивости

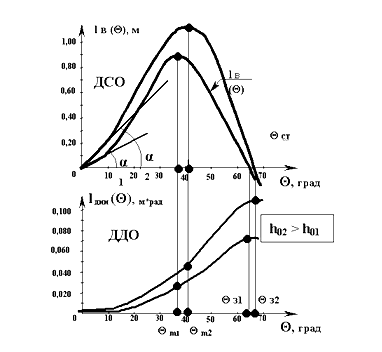
ДДО имеет две разновидности (как и соответствующие им ДСО):

Величину l_дин(θ * ) называют, по аналогии, плечом динамической остойчивости, хотя искать ему геометрическую интерпретацию не следует – эта величина получена чисто формальным путем. Размерность l_дин – [м · рад].

Однако, учитывая независимость l_дин от веса Р (и размеров) судна, возможно использовать её в задачах нормирования остойчивости, где удобно назначать универсальные константы-нормативы, которые могут использоваться на судах различного водоизмещения.

Судоводителю рекомендуют выполнять расчеты ДДО в табличной форме, где реализуется приближенный способ вычисления интеграла с переменным верхним пределом θ = θ * с использованием правила трапеций с повторениями (пример применения показан в Таблице:

Величины l_дин(θ) в четвертой колонке Табл. 1 получаются умножением значений частичной суммы Σ _част (из третьей колонки) на постоянный сомножитель, являющийся шагом интегрирования: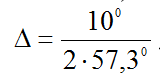Рассчитанная диаграмма статической остойчивости строится по значениям l_дин из четвертой колонки Табл.1 при значениях угла крена θ, взятых из первой колонки.

Источник

Динамическая остойчивость судна

Динамической остойчивостью называется способность судна противостоять, не опрокидываясь, динамическому воздействию внешних моментов.

До сих пор при рассмотрении вопросов остойчивости предполагалось, что кренящий момент действует на судно статически, т.е. кренящий момент m_кр был равен восстанавливающему моменту m_Θ. Это могло быть:

1) либо при столь медленном нарастании m_кр, что в любой момент осуществлялось равенство m_кр = m_Θ;

2) либо в положении судна, когда с момента m_кр приложения прошло достаточно много времени.

В действительности во многих случаях кренящий момент прикладывается к судну динамически (накат волны, шквальный ветер и т.п.). В этих случаях нарастание кренящего момента происходит быстрее, чем восстанавливающий момент и равенство между моментами не соблюдается. В результате процесс наклонения судна совершается с ускорением.

Наибольший угол крена, которого достигает судно при наклонении с ускорением, называется динамическим углом крена Θ_дин. Величина Θ_дин значительно превышает величину статического угла крена Θ_с (при m_кр.дин = m_кр.ст). Возможен случай, когда при значительном угловом ускорении величина Θ_дин окажется настолько большой, что судно опрокинется (при неопасном для судна статическом приложении равного по величине m_кр).

В теории судна при изучении динамических наклонений обычно делается допущение, что вода и воздух не оказывают сопротивления такому наклонению; это допущение привод к погрешности в безопасную сторону.

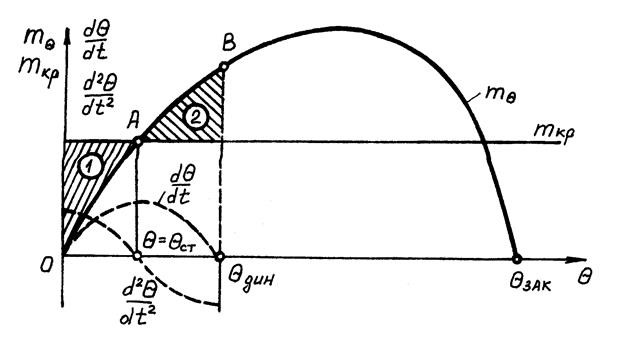
Рис.62. К рассмотрению динамических наклонений

6.3.1. Наклонение судна при динамическом воздействии кренящего момента. Предположим, что к судну, имеющему Θ = 0, динамически приложен момент m_кр, который затем продолжает дей-

ствовать статически, не изменяясь по величине с изменением угла крена Θ (рис.62).

На участке наклонения судна от Θ = 0 до Θ_ст, когда m_кр > m_Θ, происходит накопление кинетической энергии за счет избыточной работы кренящего момента, угловая скорость растет dΘ/dt, угловое ускорение d 2 Θ/dt 2 положительное, но величина его уменьшается вследствие противодействия восстанавливающего момента. При Θ = Θ_ст, когда m_кр = m_Θ, скорость наклонения судна и кинетическая энергия достигают максимальных значений, а ускорение равно нулю.

На участке наклонения судна от Θ_ст до Θ_дин, когда m_кр

Рис.63. К определению динамических углов крена судна.

6.3.2. Определение динамического угла крена судна. Запас динамической остойчивости. Величину угла Θ_дин при воздействии на судно момента m_кр заданной величины можно найти с помощью равенства работ А_кр = А_Θ при наклоне Θ = Θ_дин

(m_кр – m_Θ) dΘ = 0,

или (m_кр – m_Θ) dΘ + (m_кр – m_Θ) dΘ = 0

или (m_кр – m_Θ) dΘ = ( m_Θ – m_кр) dΘ

На рис. 63 работа кренящего момента А_кр представляет собой прямоугольник ОКВD, а работа восстанавливающего момента А_Θ криволинейную трапецию ОАМВD. Заштрихованные площади 1(ОКА) и 2 (АМВ) соответствуют избыточным работам кренящего δА_кр и восстанавливающего моментов δА_Θ.

Следовательно, угол Θ_дин может быть определен по диаграмме статической остойчивости графически из условия равенства по величине площадей 1 и 2.

Как видно из рис.63, при типичном виде диаграммы статической остойчивости Θ_дин » 2 Θ_ст.

Из сказанного выше очевидно, что работа восстанавливающего момента может служить мерой динамической остойчивости судна. Площадь на ДСО под кривой m_Θ (Θ) ОАМВN (на рис.63), характеризующую собой работу А_Θ, называют запасом динамической остойчивости судна (ЗДО). Чем больше эта площадь, тем большей динамической остойчивостью обладает судно при плавании в прямом положении. При рассмотрении рисунка 55, становится очевидным, что чем меньше метацентрическая высота судна, тем меньше не только запас статической остойчивости, но и динамической. При плавании судна

со статическим углом крена Θ_ст.1 запас динамической остойчивости уменьшается и на рисунке 63 он определяется только площадью АМВ между кривой m_Θ (Θ) и m_кр(Θ).

6.3.3. Пределы динамической остойчивости судна. Такими пределами являются:

— максимальный кренящий момент m_{кр.дин.max}, динамическое приложение которого еще не вызывает опрокидывание судна (опрокидывающий момент);

— максимальный динамический угол крена Θ_дин.max.

Для нахождения величин m_{кр.дин.max} и Θ_дин.max можно использовать диаграмму статической остойчивости (рис.63). По мере увеличения m_кр. угол Θ_дин растет. При некотором m_кр. = m_{кр.дин.max}, что соответствует предельному случаю равенства площадей 1 и 2, когда еще может быть обеспечено равенство избыточных работ восстанавливающего и кренящего моментов, угол Θ_дин = Θ_дин.max. Следовательно, Θ_дин.max определяется точкой пересечения графика m_кр(Θ), отвечающего m_{кр.дин.max}, с нисходящей ветвью ДСО.

Источник

Динамическая остойчивость

Осто́йчивость — способность плавучего средства противостоять внешним силам, вызывающим его крен или дифферент и возвращаться в состояние равновесия по окончании возмущающего воздействия. Также — раздел теории корабля, изучающий остойчивость.

Равновесием считается положение с допустимыми величинами углов крена и дифферента (в частном случае, близкими к нулю). Отклоненное от него плавсредство стремится вернуться к равновесию. То есть остойчивость проявляется только тогда, когда имеется выведение из равновесия.

Остойчивость — одно из важнейших мореходных качеств плавучего средства. Применительно к судам используется уточняющая характеристика остойчивость судна. [1] Запасом остойчивости называется степень защищённости плавучего средства от опрокидывания.

Внешнее воздействие может быть обусловлено ударом волны, порывом ветра, сменой курса и т. п.

Содержание

Виды остойчивости

Начальная поперечная остойчивость

При крене остойчивость рассматривается как начальная при углах до 10-15°. В этих пределах восстанавливающее усилие пропорционально углу крена и может быть определено при помощи простых линейных зависимостей.

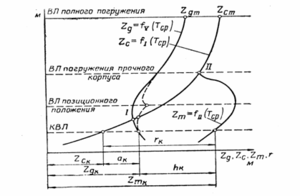
При этом делается допущение, что отклонения от положения равновесия вызываются внешними силами, которые не изменяют ни вес судна, ни положение его центра тяжести (ЦТ). [2] Тогда погруженный объем не изменяется но величине, но изменяется по форме. Равнообъемным наклонениям соответствуют равнообъемные ватерлинии, отсекающие равные по величине погруженные объемы корпуса. Линия пересечения плоскостей ватерлиний называется осью наклонения, которая при равнообъемных наклонениях проходит через центр тяжести площади ватерлинии. При поперечных наклонениях она лежит в диаметральной плоскости.

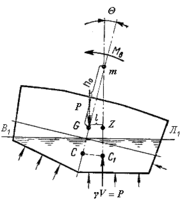
Центр тяжести G при таком наклонении не меняет своего положения, а центр величины (ЦВ) С как центр тяжести погруженного объема перемещается по некоторой кривой СС₁ в сторону наклонения и занимает новое положение C₁. Перемещение центра величины происходит вследствие изменения формы погруженного объема: с левого борта он уменьшился, а с правого борта увеличился. Сила плавучести γV, приложенная в центре величины, направлена по нормали к траектории его перемещения.

Метацентр

При малых наклонениях в поперечной плоскости линии действия сил плавучести пересекаются в одной точке m, которая называется метацентром (в данном случае — поперечным метацентром). Поперечный метацентр можно еще определить как центр кривизны кривой, по которой перемещается центр величины при наклонениях в поперечной плоскости. В общем случае наклонения (на большой угол и в любой плоскости) центр величины описывает некоторую сложную кривую, и метацентр занимает различные положения. При малых углах наклонения в поперечной плоскости можно считать, что центр величины перемещается по дуге окружности, а поперечный метацентр занимает постоянное место в диаметральной плоскости.

Радиус кривизны траектории, по которой перемещается центр величины при поперечных наклонениях называется поперечным метацентрическим радиусом r. Другими словами — это расстояние между поперечным метацентром и центром величины r = mС.

Характеристики остойчивости

В результате смещения ЦВ при наклонении линии действия силы веса и силы плавучести смещаются и образуют пару сил. Если плечо пары положительно, возникающий момент m_в действует в сторону восстановления равновесия, то есть спрямляет. Тогда говорят, что судно остойчиво. Если ЦТ расположен слишком высоко, момент может быть нулевым или отрицательным, и способствовать опрокидыванию — в этом случае судно неостойчиво.

Возвышение над основной плоскостью поперечного метацентра (z_m), центра величины (z_c), а также величина поперечного метацентрического радиуса r в значительной степени определяют остойчивость судна и зависят от величины его объемного водоизмещения, формы корпуса и посадки. Зависимость величины поперечного метацентрического радиуса от формы корпуса (величины площади ватерлинии и ее формы) и объёмного водоизмещения выглядит как:

, (1)

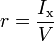
где I_x — момент инерции площади действующей ватерлинии относительно продольной оси, проходящей через центр её тяжести, м 4 ; V — объёмное водоизмещение (погруженный объём), м³.

Из рассмотрения трёх возможных вариантов воздействия сил Р и γV на при наклонениях можно сделать вывод, что для обеспечения остойчивого положения равновесия судна необходимо, чтобы метацентр находился выше центра тяжести. Поэтому возвышение поперечного метацентра над центром тяжести выделяется в особую величину и называется поперечной метацентрической высотой h. Величина h может быть выражена как:

, (2)

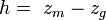
где z_m и z_g высоты метацентра и центра тяжести над основной плоскостью, соответственно.

Величина восстанавливающего момента зависит от веса судна и плеча поперечной остойчивости. Из треугольника GmZ плечо остойчивости может быть выражено через поперечную метацентрическую высоту GZ = m_G sinθ = h sinθ. Тогда восстанавливающий момент будет определяться по формуле:

, (3)

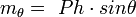
которая называется метацентрической формулой поперечной остойчивости. При малых углах крена, когда можно считать, что sinθ = θ в радианах, восстанавливающий момент определяется по линейной метацентрической формуле: m_θ = Ph θ.

Таким образом, величина восстанавливающего момента, определяющего сопротивление судна отклонениям, определяется, в свою очередь, величиной поперечной метацентрической высоты.

Остойчивость формы и остойчивость веса

, (4)

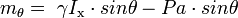
Первый член в выражении (4) в основном определяется величиной и формой площади ватерлинии и называется поэтому моментом остойчивости формы: m_ф = γ I_x sin θ. Момент остойчивости формы всегда является положительной величиной и стремится вернуть наклоненное судно в исходное положение.

Второй член в формуле (4) зависит от веса P и возвышения центра тяжести над центром величины a и называется моментом остойчивости веса m_в = − Pa sin θ. Момент остойчивости веса в случае высокого расположения центра тяжести (z_g > z_с) является величиной отрицательной, и действует в сторону наклонения.

Физическая сущность момента остойчивости формы и момента остойчивости веса раскрывается при помощи чертежа, на котором показана система сил, действующих на наклоненное судно. С накрененного борта в воду входит дополнительный объем v₁, придающий дополнительную «выталкивающую» силу плавучести. С противоположного борта из воды выходит объем v₂, стремящийся погрузить этот борт. Оба они работают на спрямление.

Погруженный объем V₁, отвечающий посадке по ватерлинию B₁Л₁, представляется в виде алгебраической суммы трех объемов

где: V — погруженный объем при исходной посадке по ватерлинию ВЛ;

v₁ — вошедший в воду, а v₂ — вышедший из воды клиновидные объёмы;

Момент сил плавучести клиновидных объемов v₁ и v₂ является моментом остойчивости формы. Чем шире корпус в районе ватерлинии, тем больше клиновидные объемы и их плечи при наклонениях в поперечной плоскости, тем больше момент остойчивости формы. Величина момента остойчивости формы определяется в основном моментом инерции площади ватерлинии относительно продольной оси I_x. А момент инерции I_x пропорционален квадрату ширины площади ватерлинии.

Момент пары сил Р и γV является моментом остойчивости веса. Он обусловлен несовпадением точек приложения сил тяжести и плавучести (G и С) в исходном положении равновесия, вследствие чего при наклонениях линии действия этих сил расходятся, и силы Р и γV образуют пару.

Меры начальной остойчивости

Для практики недостаточно простой качественной оценки — остойчиво судно или неостойчиво, так как степень остойчивости может быть различной, в зависимости от размеров, нагрузки и величины наклонения. Величины, дающие возможность количественно оценить начальную остойчивость, называются мерами начальной остойчивости.

Использование восстанавливающего момента в качестве меры начальной остойчивости неудобно, так как он зависит от угла наклонения. При бесконечно малых углах крена восстанавливающий мо­мент m_θ также стремится к нулю и по нему невозможно оценить остойчивость.

В связи с этим за меру начальной остойчивости принимается не сам восстанавливающий момент, а его первая производная по углу наклонения. Эта производная характеризует интенсивность нарастания восстанавливающего момента при наклонениях и называется коэффициентом остойчивости. При наклонениях в поперечной плоскости коэффициент поперечной остойчивости равен первой производной от восстанавливающего момента

, и при крене равном нулю K_θ = Ph.

Коэффициент остойчивости дает абсолютную оценку остойчивости, т. е. непосредственно показывает то сопротивление, которое оказывает судно отклоняющим его от положения равновесия силам. Зависимость коэффициента остойчивости от веса судна ограничивает его использование, поскольку чем больше водоизмещение, тем больше коэффициент остойчивости. Для оценки степени совершенства судна с точки зрения его начальной остойчивости используется отно­сительная мера остойчивости — метацентрическая высота, которую можно рассматривать как коэффициент остойчивости, приходящийся на тонну водоизмещения:

Благодаря своему простому геометрическому смыслу метацентрическая высота наиболее часто используется в качестве меры начальной остойчивости, хотя следует иметь в виду, что коэффициент остойчивости дает наиболее полную оценку этого мореходного качества.

Начальная продольная остойчивость

Продольная остойчивость определяется теми же зависимостями, что и поперечная.

Под воздействием внешнего дифферентующего момента M_диф судно, плавающее в положении равновесия на ровный киль (ватерлиния ВЛ), наклоняется в продольной плоскости на угол Ψ, (ватерлиния B₁Л₁). Перемещение центра величины вследствие изменения формы погруженного объема обеспечивает появление продольного восстанавливающего момента

где GK — плечо продольной остойчивости. Точка М является продольным метацентром, возвышение продольного метацентра над центром тяжести — продольной метацентрической высотой Н, а расстояние между продольным метацентром и центром величины — продольным метацентрическим радиусом R.

Продольный восстанавливающий момент при малых углах дифферента определяется по формулам: M_φ = PH·sin ψ, M_ψ = РН·ψ, которые называются метацентрическими формулами продольной остойчивости. Эти зависимости для продольного восстанавливающего момента справедливы при yглах дифферента до 0,5÷1,0°, поэтому продольная остойчивость рассматривается как начальная только в этих пределах.

Продольный метацентрический радиус определяется по формуле:

, (5)

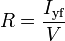
Таким образом, продольный момент остойчивости формы М_ψ = γ I_yf· sin ψ, а момент остойчивости веса М_в = — Pa· sin ψ.

Сравнивая моменты остойчивости формы и веса при поперечных и продольных наклонениях по формулам (4) и (6), видим, что остойчивость веса в обоих случаях одинакова (при условии θ = ψ), но остойчивость формы сильно отличается. Продольный момент остойчивости формы значительно больше поперечного, поскольку I_yf примерно на два порядка больше I_x. Действительно, момент инерции площади ватерлинии относительно продольной оси I_x пропорционален квадрату ширины этой площади, а момент инерции площади ватерлинии относительно поперечной оси I_yf — квадрату длины той же площади.

Если величина поперечной метацентрической высоты составляет десятые доли метра, то продольная метацентрическая высота лежит в пределах H = (0,8 ÷ 1,5) L, где L — длина по ватерлинии, м.

Доля моментов остойчивости формы и веса в обеспечении поперечной и продольной остойчивости неодинакова. При поперечных наклонениях, момент остойчивости веса составляет значительную долю от момента остойчивости формы. Поэтому поперечный вocстанавливающий момент составляет ≈ 30% от момента остойчивости формы. При продольных наклонениях момент остойчивости веса составляет всего лишь 0,5÷1,0% от момента остойчивости формы, то есть продольный восстанавливающий момент практически равен моменту остойчивости формы.

Коэффициент продольной остойчивости Кψ определяется по формуле:

При наклонениях в любых других плоскостях, отличных от поперечной и продольной, величины метацентрических радиусов и метацентрических высот (а, следовательно, и остойчивость) имеют промежуточные значения между максимальным и минимальным, соответствующим продольным и поперечным наклонениям.

Диаграмма остойчивости

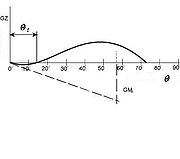
Диаграммой остойчивости называется зависимость восстанавливающего усилия от угла наклонения. Иногда называется диаграммой Рида, в честь инженера, который ввел ее в обиход. Для поперечной остойчивости (для которой и была исходно составлена Ридом) координатами будут угол крена Θ и плечо восстанавливающего момента GZ. Можно заменить плечо на сам момент M, от этого вид диаграммы не меняется.

Обычно на диаграмме изображается крен на один борт (правый), при котором углы и моменты считаются положительными. Если продолжить ее на другой борт, крен и восстанавливающий (спрямляющий) момент меняют знак. То есть диаграмма симметрична относительно начальной точки.

Основные элементы диаграммы остойчивости

Начальная точка O, она же обычно точка равновесия. В этот момент крен Θ = 0, спрямляющий момент отсутствует GZ = 0. Если почему-либо начальная остойчивость отрицательна, точка равновесия может не совпадать с началом координат. Тогда GZ = 0 при Θ = Θ₁.

Точка максимума. Представляет угол, при котором спрямляющий момент максимален GZ_max. До этого угла дальнейшее наклонение вызывает рост момента. После достижения максимума наклонение сопровождается падением момента, до достижения третьей характерной точки:

Точка заката C. Представляет угол, при котором спрямляющий момент падает до нуля GZ = 0. Соответствует точке опрокидывания судна, поскольку спрямляющих сил больше нет. Для обычных водоизмещающих судов угол заката (статический) лежит в районе 65÷75°. Для килевых яхт — в районе 120÷125°.

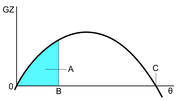
Кривизна. Характеризует скорость нарастания спрямляющего момента. Первой производной является работа. Касательная к кривой остойчивости в точке O характеризует начальную метацентрическую высоту. Ордината ее, отложенная при угле Θ = 1 рад равна метацентрической высоте h.

Площадь под кривой для текущего угла B представляет работу A восстанавливающего момента и является мерой динамической остойчивости.

Виды диаграммы остойчивости

Факторы, влияющие на изменение остойчивости

Перемещение грузов

Продольная и поперечная метацентрическне высоты изменяются на одну и ту же величину:

Величина приращения поперечного н продольного коэффициентов остойчивости также одинакова:

Метацентрические высоты и коэффициенты остойчивости после перемещения груза принимают значения:

При горизонтально-поперечном перемещении груза из точки А в точку В судно кренится от прямого положения равновесия (ватерлиния ВЛ) на угол θ (ватерлиния B₁Л₁). Такое перемещение груза можно представить так, будто груз в точке В снят (сила р направлена в противоположную сторону — вверх), а в точке E принят.

Наклонению препятствует восстанавливающий момент m_θ = Ph·sinθ. Судно будет находиться в равновесии тогда, когда кренящий и спрямляющий моменты сравняются:

где l_y = BE. Отсюда определяется угол крена равновесного положения:

Перемещение груза вызывает сдвиг центра тяжести судна в сторону перемещения груза на расстояние GG₁ = p l_y / P. Центр величины при наклонении перемещается в сторону наклонения до тех пор, пока не окажется на одной вертикали с центром тяжести, т.е. пока не будет выполнено второе условие равновесия.

Поперечная метацентрическая высота после переноса груза определяется из треугольника GmG₁:

При малых углах крена cosθ ≈ 1; h₁ ≈ h, то есть начальная поперечная остойчивость при горизонтально-поперечном перемещении груза практически не изменяется.

Формулы для определения посадки и остойчивости в случае горизонтально-продольного перемещения груза выводятся аналогично предыдущим. Из равенства дифферентующего момента от перемещения груза М_диф = p (x1 – x2) cosψ и восстанавливающего момента М_ψ = PH sinψ определяется угол дифферента, который получает судно после перемещения груза:

Начальная продольная остойчивость от горизонтально-продольного перемещения груза также практически не меняется.

Прием и снятие грузов

Прием или снятие грузов изменяет как нагрузку судна (вес и координаты центра тяжести), так и его погруженный объем (его величину, форму, координаты центра величины).

Приём груза в произвольное место можно представить как приём этого груза без изменения крена и дифферента, а затем перенос его в назначенное место. Условием неизменности крена и дифферента приема груза р является расположение его центра тяжести на одной вертикали с центром величины дополнительно входящего в воду объёма δV, который равен p/γ, где γ — удельный вес воды. При приеме относительно малого груза можно считать, что для исключения крена и дифферента он должен быть помещен на одну вертикаль с центром тяжести F исходной площади ватерлинии.

Влияние перемещений груза на остойчивость и посадку рассмотрено выше. Для определения метацентрических высот после приёма груза необходимо найти координаты центра тяжести z_g1, и метацентров z_c1 + r₁ и z_c1 + R₁. Новое положение центра тяжести находится из условия равенства статических моментов сил тяжести относительно основной плоскости.

В общем случае приёма или снятия нескольких грузов новое положение центра тяжести определяется по формуле

где: p_i — вес принятого или снятого отдельно груза, при этом принимаемый груз берется со знаком плюс, а снимаемый — со знаком минус; z_pi — аппликата центра тяжести принятого или снятого груза.

При приеме относительно небольших грузов (менее 10 % водоизмещения) на надводный корабль (судно) считается, что форма и площадь действующей ватерлинии не меняются, а погруженный объем линейно зависит от осадки — то есть принимается гипотеза прямобортности. Тогда коэффициенты остойчивости выражаются как:

В более сложных случаях используется диаграмма плавучести и начальной остойчивости, с которой снимают значения погруженного объема, метацентрического радиуса, координат ЦТ и ЦВ в зависимости от осадки. Ее использование характерно для определения остойчивости погружаемых аппаратов, например подводных лодок.

Свободные поверхности

Все рассмотренные выше случаи предполагают, что центр тяжести судна неподвижен, то есть нет грузов, которые перемещаются при наклонении. Но когда такие грузы есть, их влияние на остойчивость значительно больше остальных.

Типичным случаем являются жидкие грузы (топливо, масло, балластная и котельная вода) в цистернах, заполненных частично, то есть имеющих свободные поверхности. Такие грузы способны переливаться при наклонениях. Если жидкий груз заполняет цистерну полностью, он эквивалентен твердому закрепленному грузу.

Если жидкость заполняет цистерну не полностью, т.е. имеет свободную поверхность, занимающую всегда горизонтальное положение, то при наклонении судна на угол θ жидкость переливается в сторону наклонения. Свободная поверхность примет такой же угол относительно КВЛ.

Уровни жидкого груза отсекают равные по величине объёмы цистерн, т.е. они подобны равнообъёмным ватерлиниям. Поэтому момент, вызываемый переливанием жидкого груза при крене δm_θ, можно представить аналогично моменту остойчивости формы m_ф, только δm_θ противоположно m_ф по знаку:

где i_x — момент инерции площади свободной поверхности жидкого груза относительно продольной оси, проходящей через центр тяжести этой площади, γ_ж — удельный вес жидкого груза

Тогда восстанавливающий момент при наличии жидкого груза со свободной поверхностью:

где h — поперечная метацентрическая высота в отсутствие переливания, h₁ = h − γ_ж i_x /γV — фактическая поперечная метацентрическая высота.

Плотности воды и жидкого груза относительно стабильны, то есть основное влияние на поправку оказывает форма свободной поверхности, точнее ее момент инерции. А значит, на поперечную остойчивость в основном влияет ширина, а на продольную длина свободной поверхности.

Физический смысл отрицательного значения поправки в том, что наличие свободных поверхностей всегда уменьшает остойчивость. Поэтому принимаются организационные и конструктивные меры для их уменьшения:

Динамическая остойчивость

В отличие от статического, динамическое воздействие сил и моментов сообщает судну значительные угловые скорости и ускорения. Поэтому их влияние рассматривается в энергиях, точнее в виде работы сил и моментов, а не в самих усилиях. При этом используется теорема кинетической энергии, согласно которой приращение кинетической энергии наклонения судна равно работе действующих на него сил.

Когда к судну прикладывается кренящий момент m_кр, постоянный по величине, оно получает положительное ускорение, с которым начинает крениться. По мере наклонения возрастает восстанавливающий момент, но вначале, до угла θ_cт, при котором m_кр = m_θ, он будет меньше кренящего. По достижении угла статического равновесия θ_cт, кинетическая энергия вращательного движения будет максимальной. Поэтому судно не останется в положении равновесия, а за счет кинетической энергии будет крениться дальше, но замедленно, поскольку восстанавливающий момент больше кренящего. Накопленная ранее кинетическая энергия погашается избыточной работой восстанавливающего момента. Как только величина этой работы будет достаточной для полного погашения кинетической энергии, угловая скорость станет равной нулю и судно перестанет крениться.

Наибольший угол наклонения, которое получает судно от динамического момента, называется динамическим углом крена θ_дин. В отличие от него угол крена, с которым судно будет плавать под действием того же момента (по условию m_кр = m_θ), называется статическим углом крена θ_ст.

Если обратиться к диаграмме статической остойчивости, работа выражается площадью под кривой восстанавливающего момента m_в. Соответственно, динамический угол крена θ_дин можно определить из равенства площадей OAB и BCD, соответствующих избыточной работе восстанавливающего момента. Аналитически та же работа вычисляется как:

,

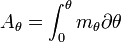
на интервале от 0 до θ_дин.

Достигнув динамического угла крена θ_дин, судно не приходит в равновесие, а под действием избыточного восстанавливающего момента начинает ускоренно спрямляться. При отсутствии сопротивления воды судно вошло бы в незатухающие колебания около положения равновесия при крене θ_ст с амплитудой от 0 до θ_дин. Но практически, от сопротивления воды колебания быстро затухают и оно остается плавать со статическим углом крена θ_ст.

Динамическое воздействие кренящего момента всегда опаснее статического, так как приводит к более значительным наклонениям. В пределах прямолинейной части диаграммы статической остойчивости, динамический угол крена примерно в два раза больше статического: θ_дин ≈ 2 θ_ст.

Источник