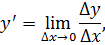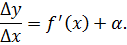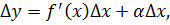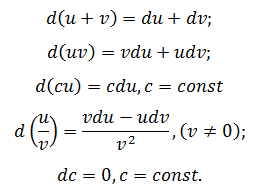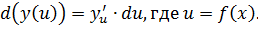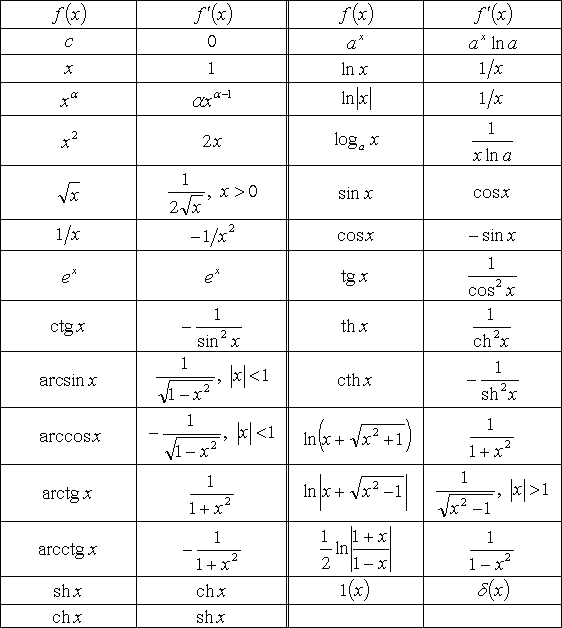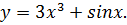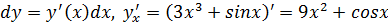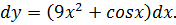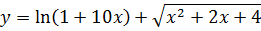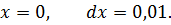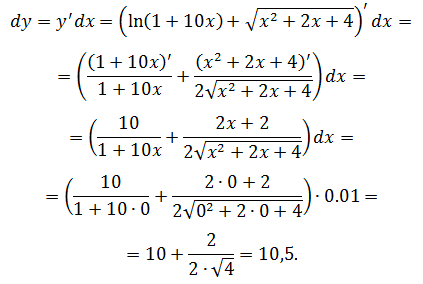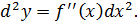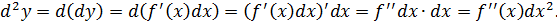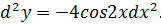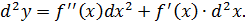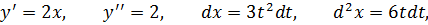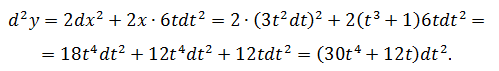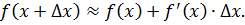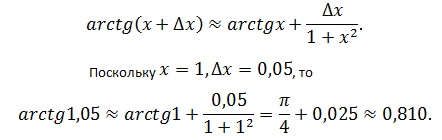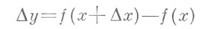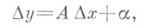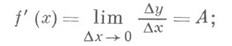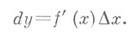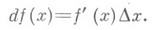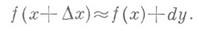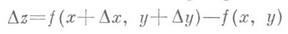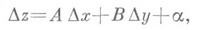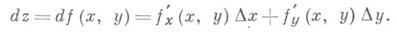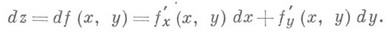Что такое дифференциал матанализ

При выполнении некоторых расчётов в исследованиях, проектировании, анализе полученных опытных путём данных часто возникает необходимость предварительной прикидки результата, которую удобно выполнять, используя дифференциал функции. Приближённые вычисления, выполненные с его помощью, могут дать новые направления дальнейшего изучения объектов и их разработок.

Понятие и геометрический смысл дифференциала

Пусть y = f (x) имеет производную

Применяя свойства предела функции, получают равенство

После умножения обеих частей на приращение аргумента Δx, образуется тождество:

в котором в правой части записано слагаемое, являющееся бесконечно малой одного порядка с Δx, далее идет слагаемое более высокого порядка.

Определение 1

Дифференциалом функции y = f (x) первого порядка называется главная часть её приращения f′(x)Δx, которую обозначают dy (или d(f(x)).

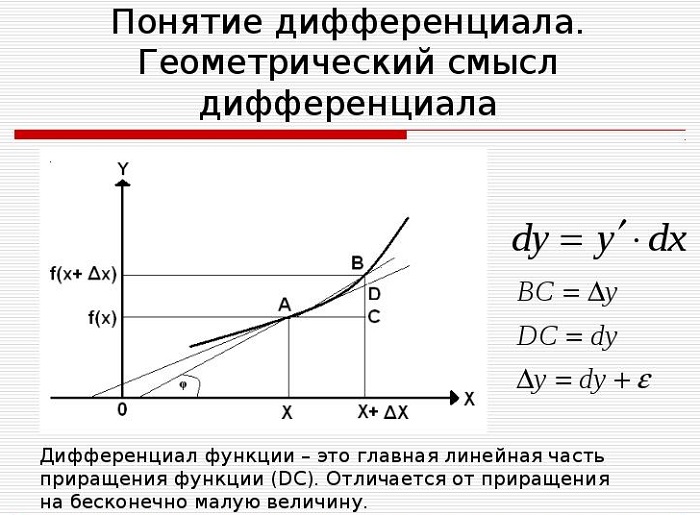
Для наглядного представления и понимания определения рассматривается касательная к графику функции y = f(x) в точке x. Когда значение переменной сдвигается по построенной прямой (получает приращение) на некоторую малую величину Δx, значение второй координаты точки тоже меняется.

Значит, дифференциал функции y = f(x) в точке x равен приращению ординаты касательной, когда её абсцисса меняется на величину Δx.

Определение 2

Дифференциал от дифференциала называется дифференциалом второго порядка. Таким же рекуррентным образом вводятся понятия дифференциалов более высоких порядков.

Формы записи дифференциала

Для нахождения дифференциала независимой переменной рассматривают функцию y = x, учитывая, что x’ = 1, а, следовательно:

Отсюда получается формула:

Для второго порядка вводится обозначение d 2 y.

Свойства дифференциала

Существующая таблица производных помогает выделить некоторые свойства дифференциалов, например, для суммы, произведения, частного получаются следующие правила:

Одним из важных свойств является инвариантность (неизменность) формы записи, независимо от того, является ли функция элементарной или композицией элементарных (сложной). Фактически,

Примеры решения задач

Задача №1

Найти дифференциал функции

Задача №2

Вычислить значение дифференциала функции

В помощь студентам создан онлайн калькулятор, который позволяет ввести функцию, нажать кнопку и получить форму или значение дифференциала.

Если dx есть константа, то для высших порядков имеет место следующая формула:

Этот результат вытекает непосредственно из определения:

Задача №3

Найти d 2 y, если y = cos2x и x – независимая переменная.

Если x – функция от некоторой другой независимой переменной, то свойство инвариантности перестаёт работать, следовательно,

Задача №4

Найти d 2 y, если y = x 2 и x = t 3 + 1, t – независимый аргумент.

Нетрудно заметить, что если выразить y напрямую через t, то получится тот же результат.

с высокой степенью точности можно вычислить приращение любой дифференцируемой зависимости.

Раскрыв Δy, сделав соответствующие преобразования, приходят к формуле приближённых вычислений:

Задача №5

Вычислить приближённо arctg1,05.

Пусть f(x) = arctg x. Тогда

Полный дифференциал функции

Математика не ограничивается множеством функций одного независимого аргумента. Рассматриваются зависимости от двух и более переменных.

Определения похожи, отличается вид главной части. Рассматриваются несколько слагаемых.

Например, если z = f(x;y) то

Последнее равенство есть формула полного дифференциала. Для функции нескольких переменных сохраняется принцип построения.

Если рассматривают приращения только по одной переменной, то приходят к понятию частных дифференциалов.

Заключение

Высшая математика позволяет находить приближённо общий корень системы уравнений, пользуясь дифференциальным исчислением, делать прикидку результатов, прогнозировать получаемое.

Источник

ДИФФЕРЕНЦИАЛ

— главная линейная часть приращения функции.

1) Действительная функция y = f )действительного переменного наз. дифференцируемой в точке х, если она определена в нек-рой окрестности этой точки и если существует такое число А, что приращение

(при условии, что точка х+Ах лежит в упомянутой окрестности) может быть представлено в виде

где при При этом А Ах обозначается через dy и наз. дифференциалом функции f(х)в точке х. Д. dy при фиксированном хпропорционален Ах, т. е. является линейной функцией от D х. Дополнительный член a при является, в силу определения, бесконечно малой более высокого порядка по сравнению с D х (и по сравнению с dy, если ). Именно в этом смысле Д. и наз. главной частью приращения функции.

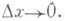
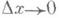
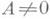
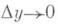
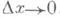
Для функции, дифференцируемой в точке х, при , т. е. функция, дифференцируемая в некоторой точке, непрерывна в ней. Функция f(x)дифференцируема в точке хв том и только в том случае, если она имеет в этой точке конечную производную

Существуют непрерывные, но не дифференцируемые функции.

Кроме обозначения dy используется обозначение df(x);тогда предыдущее равенство принимает вид

Приращение аргумента Ах обозначается также через dx и наз. дифференциалом независимого переменного. Поэтому можно писать

Отсюда f(x)=dyldx, т. е. производная равна отношению Д. dy и dx. Если А=0, то 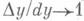при Dx->0, т. е. Ау и dy при являются в случае А неравно 0 эквивалентными бесконечно малыми; этим, рав, но как и простой структурой Д. (линейностью по Ах), часто пользуются в приближенных вычислениях, полагая Dy=dy при малых D х. Если хотят, напр., вычислить f(x+Dx), зная f)(Dxмало), то полагают

Конечно, такое рассуждение имеет ценность, если можно оценить соответствующую погрешность.

При этом a= Dу-dy, т. е. значение |a| совпадает с длиной отрезка TS.

2) Определение дифференцируемости и Д. естественным образом обобщается на действительные функции от пдействительных переменных. Напр., в случ. п=2 действительная функция z=f(x, у)наз. дифференцируемой в точке ( х, у )по совокупности переменных хи у, если она определена в нек-рой окрестности этой точки и ее полное приращение

может быть представлено в виде

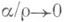
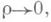
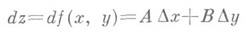
где Аи В- некоторые числа, при r=предполагается, что точка ( х+D х, у+Dy). принадлежит упомянутой окрестности (см. рис. 2) При этом вводится обозначение и dz наз. полным дифференциалом, или просто дифференциалом, функции f(x,у). в точке ( х, у )(иногда с добавлением: «по совокупности переменных хи у»). Для фиксированной точки ( х, у )Д. dz есть линейная функция от Ах и Ау;разность а= Az-dz есть бесконечно малая более высокого порядка по сравнению с р. В этом смысле dz есть главная линейная часть приращения Az.

Если f(x, у )дифференцируема в точке ( х, у), то oн непрерывна в этой точке и имеет в ней конечные частные производные

Приращения Ах и Ау независимых переменных, как и в случае одного переменного, обозначаются dx и dу По этой причине можно написать

Существование конечных частных производных, во обще говоря, не влечет дифференцируемости функции (даже если предполагать заранее ее непрерывность) здесь нарушается аналогия с функциями одного переменного.

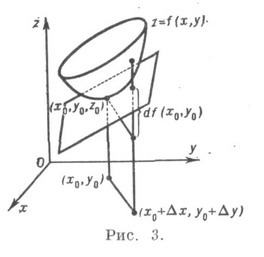
Если функция f(x, у )имеет в точке ( х, у )частную производную по х, то произведение f_x(x, y)dx наз. частным дифференциалом по х;аналогично, f’_y(x, y)dy есть частный Д. по у. Если функция дифференцируема, то ее полный Д. равен сумме частных Д. Геометрически полный Д. df(x₀, у ₀ )есть приращение аппликаты касательной плоскости поверхности z-f(x, у )в точке ( х ₀, у ₀, z₀), где z₀=f(z₀, у ₀ )(см. рис. 3).

Это показывает, в частности, что не всякое выражение с непрерывными А и В (вобласти D)является в этой области полным Д. нек-рой функции двух переменных. В этом состоит еще одно нарушение аналогии с функциями одного переменного, где любое выражение A(x)dx с непрерывной в нек-ром промежутке функцией (х). служит Д. для нек-рой функции.

Выражение Adx+Bdy является полным Д. нек-рой функции z=f(x, у), в односвязной открытой области D, если ( х, у )и В( х, у )непрерывны в этой области и удовлетворяют условию А’ =В’ _Х и при этом а) А’_y и В’ _х непрерывны или б) ( х, у) и В( х, у) дифференцируемы по совокупности переменных хи увсюду в D(см. [7], [8]).

О Д. действительных функций одного или нескольких действительных переменных и о Д. высших порядков см. также Дифференциальное исчисление.

3) Пусть функция f(x)определена на нек-ром множестве Едействительных чисел, х- предельная точка этого множества, Dy=АDx+a, где

при ; тогда функция f(x)наз. дифференцируемой по множеству Ев точке х,a dy=AD х наз. ее дифференциалом» по множеству Еточке х. Это есть обобщение Д. действительной функции одного действительного переменного. Разновидностями этого обобщения являются Д. в концах промежутка, на котором определена функция, и аппроксимативный Д. (см. Аппроксимативная дифференцируемоетъ).

Подобным же образом вводится Д. по множеству для действительных функций многих действительных переменных.

4) Все эти определения дифференцируемости и Д. почти без изменений распространяются соответственно на комплексные функции одного или нескольких действительных переменных, на действительные и комплексные вектор-функции одного или нескольких действительных переменных, на комплексные функции и вектор-функции одного или нескольких комплексных переменных. В функциональном анализе они распространяются на функции точки абстрактного пространства. Можно говорить о дифференцируемости и Д. функции множества по отношению к нек-рой мере.

Источник

Что такое дифференциал функции?

Понятие дифференциала функции связано с такими важными математическими разделами как дифференциальное и интегральное исчисление и тесно связано с понятием производной функции. Наиболее часто дифференциал применяется для приближенных вычислений, а также для оценки погрешностей формул и измерений.

Дифференциал функции — это линейная часть приращения функции. Говоря о значении дифференциала функции, рассматривают конкретную точку функции и бесконечно малое изменение аргумента.

История открытия дифференциала

Чаще всего открытие дифференциально-интегрального исчисления принято связывать с именем Исаака Ньютона, однако, этот факт активно оспаривают учёные со всего света.

Действительно, открытие целого нового направления в науке, столь значимого для её развития, было бы ошибочно считать заслугой только одного учёного. Изначально интегрирование связывали с вычислением площадей и объёмов криволинейных фигур. Такие задачи, как известно, решались ещё во времена Архимеда, поэтому его имя также имеет отношение к открытию дифференциального исчисления.

Также дифференцирование имеет отношение к решению задач на проведение касательных к различным кривым. Данное направление активно развивали греческие математики. В те времена математики столкнулись с трудностью, которую не смогли решить в дальнейшем и представители Нового времени.

Дело в том, что для определения направления прямой требовалось знать координаты как минимум двух точек, а касательная имеет лишь одну точку соприкосновения с кривой. Этот факт натолкнул учёных на мысль о том, что в одной точке кривая может иметь несколько касательных. В то время ученые пришли к выводу, что прямая состоит не из точек, а из отрезков минимальной длины. Таким образом, они считали направление касательной в некоторой точке совпадающим с направлением атомарного отрезка в данной точке.

В дальнейшем учёные Нового времени опровергли данную теорию. В этот период огромный вклад в развитие науки внёс Исаак Ньютон. Ученый сформулировал определения и принципы решения производных, а также основы дифференциального исчисления, которых придерживаются учёные и в наши дни.

Дифференциальное исчисление широко применяется в математике и других науках для решения различных задач.

Геометрический смысл дифференциала

Геометрический смысл дифференциала заключается в следующем: дифференциал функции f(x) равен приращению ординаты касательной к графику функции, которая проведена через некоторую точку с координатами (x,y) при изменении координаты x на величину Δх=dx.

Дифференциал является главной линейной частью функции относительно приращения аргумента. Чем меньше приращение функции, тем большая доля приращения приходится на эту линейную часть.

Таким образом, при бесконечно малом Δх, приращение функции можно считать равным ее дифференциалу. Это свойство дифференциала позволяет использовать его для приблизительных вычислений и оценки погрешностей измерений.

Применение дифференциала в приближенных вычислениях

Поскольку дифференциал функции является частью ее приращения, то при бесконечно малом приращении аргумента он приблизительно равен приращению функции. При этом чем меньше приращение аргумента, тем точнее значение функции. Этот факт даёт возможность использования дифференциалов для приближённых вычислений.

С помощью таких вычислений можно решать различные виды задач. Приближённые вычисления практически всегда связаны с наличием погрешности.

Использование дифференциала для оценки погрешностей

Результаты измерений в большинстве случаев содержат ошибку, обусловленную неточностью измерительных приборов.

Число, несколько превышающее или равное этой неточности, называется «предельной абсолютной погрешностью».

Отношение предельной погрешности к значению измеряемой величины называют «предельной относительной погрешностью».

Для оценки величины погрешностей измерений используют дифференциальное исчисление.

Источник

Что такое дифференциал матанализ

Заметим, что в данном примере коэффициент \(A\) равен значению производной функции \(S\) в точке \(:\) \[A = 2.\] Оказывается, что для любой дифференцируемой функции справедлива следующая теорема :

Коэффициент \(A\) главной части приращения функции в точке \(\) равен значению производной \(f’\left( <> \right)\) в этой точке, т.е. приращение \(\Delta y\) выражается формулой \[ <\Delta y = A\Delta x + \omicron\left( <\Delta x>\right) > = > \right)\Delta x + \omicron\left( <\Delta x>\right).> \] Разделив обе части этого равенства на \(\Delta x \ne 0,\) имеем \[ <\frac<<\Delta y>><<\Delta x>> = A + \frac <<\omicron\left( <\Delta x>\right)>><<\Delta x>> > = > \right) + \frac <<\omicron\left( <\Delta x>\right)>><<\Delta x>>.> \] В пределе при \(\Delta x \to 0\) получаем значение производной в точке \(:\) \[ > \right) = \lim\limits_ <\Delta x \to 0>\frac<<\Delta y>><<\Delta x>> > = > \right).> \] Здесь мы учли, что для малой величины \(\omicron\left( <\Delta x>\right)\) более высокого порядка малости, чем \(\Delta x,\) предел равен \[\lim\limits_ <\Delta x \to 0>\frac <<\omicron\left( <\Delta x>\right)>><<\Delta x>> = 0.\] Если считать, что дифференциал независимой переменной \(dx\) равен ее приращению \(\Delta x:\) \[dx = \Delta x,\] то из соотношения \[dy = A\Delta x = y’dx\] следует, что \[y’ = \frac<><>,\] т.е. производную функции можно представить как отношение двух дифференциалов.

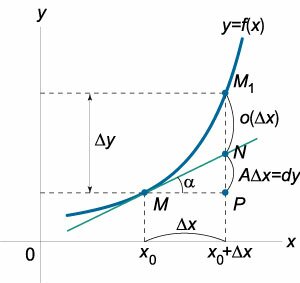
На рисунке \(2\) схематически показана разбивка приращения функции \(\Delta y\) на главную часть \(A\Delta x\) (дифференциал функции) и член высшего порядка малости \(\omicron\left( <\Delta x>\right)\).

Касательная \(MN\), проведенная к кривой функции \(y = f\left( x \right)\) в точке \(M\), как известно, имеет угол наклона \(\alpha\), тангенс которого равен производной: \[\tan \alpha = f’\left( <> \right).\] При изменении аргумента на \(\Delta x\) касательная получает приращение \(A\Delta x.\) Это линейное приращение, образованное касательной, как раз и является дифференциалом функции. Остальная часть полного приращения \(\Delta y\) (отрезок \(N\)) соответствует «нелинейной» добавке с более высоким порядком малости относительно \(\Delta x\).

Источник

Что такое дифференциал матанализ

При дифференцировании различают функции по способу их задания: явные, неявные и параметрические.

Производной функции y = f ( x ) по переменной x в некоторой точке называется предел отношения приращения функции к приращению аргумента, когда последнее стремится к нулю, то есть

Производная характеризует скорость изменения функции в достаточно малой окрестности заданной точки.

Приведем таблицу производных основных элементарных функций (без доказательства), которые рассматриваются нами как функции простые и явно заданные.

Следствие. В точках разрыва функция производной не имеет

Существуют такие точки, в которых функция непрерывна, но не дифференцируема. Так, функция y =| x | в точке x =0 непрерывна, но производной не имеет, так как в этой точке к графику функции можно провести бесконечное множество касательных (рис. 3.6). Такие точки называются угловыми или точками излома функции. Данный случай показывает, что обратное утверждение к теореме 3.9 неверно.

Среди явных функций особое место занимают обратные функции, производная которых находится с помощью следующей теоремы.

Теорема 3.10. Если строго монотонная функция y = f ( x ) дифференцируема на некотором интервале Х, причем ее производная не обращается в нуль на Х, то обратная к ней функция x = φ ( y ) также дифференцируема на этом интервале, при этом:

По определению производной можно записать:

Среди явных функций выделяют класс сложных функций.

Теорема 3.11. Чтобы продифференцировать сложную функцию необходимо сначала продифференцировать внешнюю функцию по внутренней, считая внутреннюю функцию независимой переменной, затем продифференцировать внутреннюю функцию по независимому переменному и результаты дифференцирования перемножить, то есть

Решение. Согласно формуле (3.31) и с учетом табли чных формул (3.17), (3.19), (3.29) имеем:

где t – параметр. Производную такой функции несложно получить:

Пример 3.9. Найти производную функции .

Решение. Согласно формуле (3.32) и с учетом табличных формул (3.18), (3.19) имеем:

Помимо таблицы производных имеют место правила дифференцирования.

Теорема 3.12. Производная суммы двух дифференцируемых функций равна сумме производных этих функций:

Данная теорема может быть обобщена для произвольного конечного числа функций-слагаемых.

Решение. Согласно формулам (3.33) и (3.31) и с учетом табличных формул (3.17), (3.20), (3.23) имеем:

Теорема 3.13. Производная произведения двух дифференцируемых функций равна произведению производной первой функции-сомножителя на вторую функцию плюс произведение первой функции на производную второй функции–сомножителя, то есть

Решение. Согласно формуле (3.34) и с учетом табличных формул (3.22), (3.24) имеем:

Теорема 3.14. Производная частного двух функций равна дроби, у которой знаменатель есть квадрат знаменателя данной дроби, а числитель есть разность между произведением знаменателя на производную числителя и произведением числителя на производную знаменателя, то есть

Решение. Согласно формуле (3.35) и с учетом табличных формул (3.17), (3.29) имеем:

Решение. Согласно формуле (3.31) дифференцирования сложной функции и (3.34) производной произведения, с учетом табличных формул (3.17) и (3.18) имеем:

Дифференциалом функции y = f ( x ) в точке x называется главная часть приращения этой функции, равная произведению производной функции на приращение аргумента:

Формула (3.39) применяется для вычисления приближенных значений функций.

Источник