Что такое диаметр овала

Как рассчитать радиус и диаметр овала

Овал также называют эллипсом. Из-за своей продолговатой формы овал имеет два диаметра: диаметр, который проходит через самую короткую часть овала, или полу-малую ось, и диаметр, который проходит через

Содержание:

Полу минорная ось

Измерьте расстояние между одной точкой фокусировки до точки по периметру овала, чтобы определить a. В этом примере a будет равно 5 см.

Измерьте расстояние между другой точкой фокусировки и той же точкой на периметре, чтобы определить b. В этом примере b будет равен 3 см.

Добавьте a и b вместе и возведите в квадрат сумму. Например, 5 см плюс 3 см равны 8 см, а 8 см в квадрате равны 64 см ^ 2.

Измерьте расстояние между двумя точками фокусировки, чтобы выяснить f; возвести в квадрат результат. В этом примере f равно 5 см, а квадрат 5 см равен 25 см ^ 2.

Вычтите сумму на шаге четыре из суммы на шаге три. Например, 64 см ^ 2 минус 25 см ^ 2 равняется 39 см ^ 2.

Рассчитайте квадратный корень суммы из шага пять. Например, квадратный корень из 39 равен 6,245, округленный до ближайшей тысячной. Следовательно, малая ось или самый короткий диаметр составляет 6,245 см.

Разделите измерение полу-малой оси пополам, чтобы вычислить ее радиус. Например, 6,245 см, разделенные на два, равны 3,122 см.

Полу-Большая Ось

Повторите процесс измерения из предыдущего раздела, чтобы выяснить a и b. В этом примере хорошо использовать те же цифры: 5 см и 3 см.

Добавьте a и b вместе. Результатом является большая полуось. Например, 5 см плюс 3 см равны 8 см, поэтому большая полуось составляет 8 см.

Уменьшить вдвое результат первого шага, чтобы вычислить радиус. Восемь, разделенная на два, равна четырем, поэтому другой радиус равен 4 см.

Источник

Эллипс — свойства, уравнение и построение фигуры

Среди центральных кривых второго порядка особое место занимает эллипс, близкий к окружности, обладающий похожими свойствами, но всё же уникальный и неповторимый.

Определение и элементы эллипса

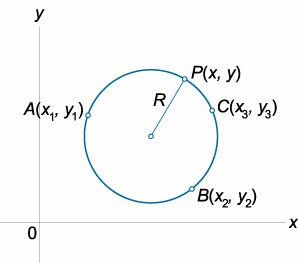
Множество точек координатной плоскости, для каждой из которых выполняется условие: сумма расстояний до двух заданных точек (фокусов) есть величина постоянная, называется эллипсом.

По форме график эллипса представляет замкнутую овальную кривую:

Наиболее простым случаем является расположение линии так, чтобы каждая точка имела симметричную пару относительно начала координат, а координатные оси являлись осями симметрии.

Отрезки осей симметрии, соединяющие две точки эллипса, называются осями. Различаются по размерам (большая и малая), а их половинки, соответственно, считаются полуосями.

Точки эллипса, являющиеся концами осей, называются вершинами.

Расстояния от точки на линии до фокусов получили название фокальных радиусов.

Расстояние между фокусами есть фокальное расстояние.

Отношение фокального расстояния к большей оси называется эксцентриситетом. Это особая характеристика, показывающая вытянутость или сплющенность фигуры.

Основные свойства эллипса

имеются две оси и один центр симметрии;

при равенстве полуосей линия превращается в окружность;

все точки фигуры лежат внутри прямоугольника со сторонами, равными большой и малой осям эллипса, проходящими через вершины параллельно осям.

Уравнение эллипса

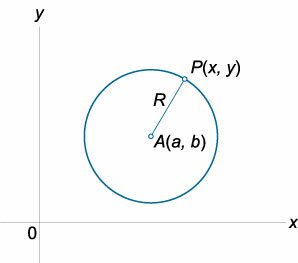
Пусть линия расположена так, чтобы центр симметрии совпадал с началом координат, а оси – с осями координат.

Для составления уравнения достаточно воспользоваться определением, введя обозначение:

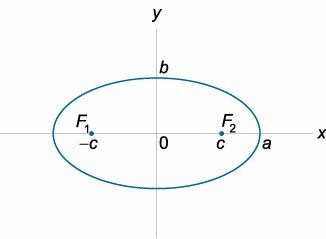
а – большая полуось (в наиболее простом виде её располагают вдоль оси Оx) (большая ось, соответственно, равна 2a);

c – половина фокального расстояния;

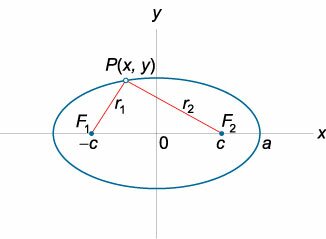
M(x;y) – произвольная точка линии.

В этом случае фокусы находятся в точках F1(-c;0); F2(c;0)

После ввода ещё одного обозначения

получается наиболее простой вид уравнения:

a 2 b 2 — a 2 y 2 — x 2 b 2 = 0,

Параметр b численно равен полуоси, расположенной вдоль Oy (a > b).

В случае (b b) формула эксцентриситета (ε) принимает вид:

Чем меньше эксцентриситет, тем более сжатым будет эллипс.

Площадь эллипса

Площадь фигуры (овала), ограниченной эллипсом, можно вычислить по формуле:

a – большая полуось, b – малая.

Площадь сегмента эллипса

Часть эллипса, отсекаемая прямой, называется его сегментом.

, где

(xo;y0) – крайняя точка сегмента.

Длина дуги эллипса

Длина дуги находится с помощью определённого интеграла по соответствующей формуле при введении параметра:

Радиус круга, вписанного в эллипс

В отличие от многоугольников, круг, вписанный в эллипс, касается его только в двух точках. Поэтому наименьшее расстояние между точками эллипса (содержащее центр) совпадает с диаметром круга:

Радиус круга, описанного вокруг эллипса

Окружность, описанная около эллипса, касается его также только в двух точках. Поэтому наибольшее расстояние между точками эллипса совпадает с диаметром круга:

Онлайн калькулятор позволяет по известным параметрам вычислить остальные, найти площадь эллипса или его части, длину дуги всей фигуры или заключённой между двумя заданными точками.

Как построить эллипс

Построение линии удобно выполнять в декартовых координатах в каноническом виде.

Строится прямоугольник. Для этого проводятся прямые:

Сглаживая углы, проводится линия по сторонам прямоугольника.

Полученная фигура есть эллипс. По координатам отмечается каждый фокус.

При вращении вокруг любой из осей координат образуется поверхность, которая называется эллипсоид.

Источник

Чем отличается эллипс от овала?

Чем отличается эллипс от овала? Данный вопрос часто остается без ответа — хоть эти две фигуры и знакомы всем еще со школьных времен. Но мало кто понимает, в чем разница между ними. И существуют ли вообще какие-либо отличия.

В чем различие?

Официальные определения каждой из фигур звучат достаточно сложно и непонятно.

Но, если откинуть заумные формулы и сложные определения — все намного проще.

Овал можно «растянуть» как угодно. Это может быть практически круг, либо узкая и длинная замкнутая кривая — главное, чтобы ее форма удовлетворяла определению.

Где а — это длинная полуось, b — короткая, а с — фокальное расстояние (от центра до фокуса).

Всем известный круг — это частный вариант эллипса. В этом случае с=0 (т.к. фокус у него один). Полуоси (радиусы) тоже равны.

Построение овалов и эллипсов

Казалось бы, а зачем их вообще строить?

Земная орбита имеет форму эллипса (траектории движения остальных планет и галактик аналогичны).

Практически в любой технике имеются круглые детали — а они при переведении в трехмерную проекцию будут изображаться в форме замкнутых кривых. Подобные примеры можно приводить бесконечно.

Поэтому в технике, космонавтике, астрономии, архитектуре и многих других научных отраслях разнообразные овалы приходится строить регулярно. Эти знания применяют даже люди, далекие от сложных вычислений — например, художники.

Для того чтобы начертить любую из этих фигур, потребуется лишь циркуль, транспортир и линейка. Сам процесс особых сложностей не вызывает, главное внимательность и точность.

На фото ниже приведен пример построения эллипса в аксонометрии (изометрия).

Формулы и интересные факты

Хоть эти две фигуры и встречаются повсеместно, они до конца не изучены. В школьном курсе их проходят довольно поверхностно, не упоминая о возможных трудностях.

Овалы часто заменяют «правильными» эллипсами, так как с ними работать проще. Но даже в этом случае возникают сложности.

Так, казалось бы, простая задача — вычислить периметр — на самом деле невыполнима. Точной формулы не существует. Это связано с тем, что каждая точка имеет свой собственный радиус кривизны.

Школьникам и людям, далеким от точных вычислений, дают приблизительную формулу. Погрешность у такого результата будет велика, но для примитивных целей это допустимо.

В серьезных расчетах используются совсем другие формулы. Но даже они не дают желаемого результата, так как имеют достаточно большие отклонения от реальных значений.

Так, при расчете траектории движения космического корабля погрешность может достигать нескольких тысяч километров (на дальних расстояниях), а это слишком много. Поэтому поиски «идеальной» формулы ведутся до сих пор.

Источник

Что такое диаметр овала

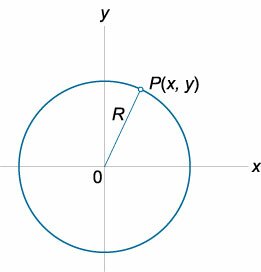
Уравнение окружности в параметрической форме
\( \left\ < \beginx &= R \cos t \\ y &= R\sin t \end \right., \;\;0 \le t \le 2\pi\),
где \(x\), \(y\) − координаты точек окружности, \(R\) − радиус окружности, \(t\) − параметр.

Сумма расстояний от любой точки эллипса до его фокусов постоянна:
\( + = 2a\),
где \(\), \(\) − расстояния от произвольной точки \(P\left( \right)\) до фокусов \(\) и \(\), \(a\) − большая полуось эллипса.

Соотношение между полуосями эллипса и фокусным расстоянием
\( = + \),
где \(a\) − большая полуось эллипса, \(b\) − малая полуось, \(c\) − половина фокусного расстояния.

Уравнение эллипса в параметрической форме
\( \left\ < \beginx &= a\cos t \\ y &= b\sin t \end \right., \;\;0 \le t \le 2\pi\),
где \(a\), \(b\) − полуоси эллипса, \(t\) − параметр.

Общее уравнение эллипса
\(A + Bxy + C + Dx + Ey + F = 0\),
где \( — 4AC Общее уравнение эллипса, полуоси которого параллельны осям координат
\(A + C + Dx + Ey + F = 0\),
где \(AC > 0\).

Периметр эллипса
\(L = 4aE\left( e \right)\),
где \(a\) − большая полуось эллипса, \(e\) − эксцентриситет, \(E\) − полный эллиптический интеграл второго рода.

Площадь эллипса
\(S = \pi ab\)

Источник

Овал. Определение овала и способы его построения

Овал — это замкнутая коробовая кривая, имеющая две оси симметрии и состоящая из двух опорных окружностей одинакового диаметра, внутренне сопряженных дугами (рис. 13.45). Овал характеризуется тремя параметрами: длина, ширина и радиус овала. Иногда задают только длину и ширину овала, не определяя его радиусов, тогда задача построения овала имеет большое множество решений (см. рис. 13.45, а. г).

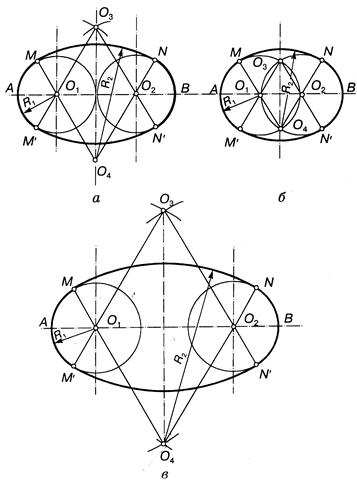
Применяют также способы построения овалов на основе двух одинаковых опорных кругов, которые соприкасаются (рис. 13.46, а), пересекаются (рис. 13.46, б) или не пересекаются (рис. 13.46, в). При этом фактически задают два параметра: длину овала и один из его радиусов. Эта задача имеет множество решений. Очевидно, что R > ОА не имеет верхней границы. В частности R = О₁О₂ (см. рис. 13.46.а, и рис. 13.46.в), а центры О₃ и О₄ определяют, как точки пересечения базовых кругов (см. рис. 13.46,б). Согласно общей теорией точки, сопряжения определяются на прямой, соединяющей центры дуг соприкасающихся окружностей.

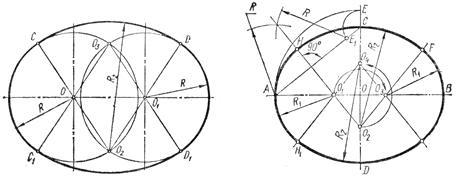
Построение овала с соприкасаю­щимися опорными окружностями (задача имеет множество решений) (рис. 3.44). Из центров опорных окружностей О и 0₁ радиусом, равным, например, расстоянию между их центрами, проводят дуги окруж­ностей до пересечения в точках О₂и О₃.

Если из точек О₂и О₃ провести прямые через центры О и O₁, то в пересечении с опорными окружнос­тями получим точки сопряжения С, C₁, D и D₁. Из точек О₂и О₃ как из центров радиусом R₂ проводят дуги сопряжения.

Построение овала с пересека­ющимися опорными окружностями (задача также имеет множество решений) (рис. 3.45). Из точек пе­ресечения опорных окружностей С₂ и О₃ проводят прямые, например, через центры О и O₁ до пересечения с опорными окружностями в точках сопряжения С, С₁ D и D₁, а ра­диусами R₂, равными диаметру опорной окружности,— дуги со­пряжения.

Рисунок 3.45 Рисунок 3.46

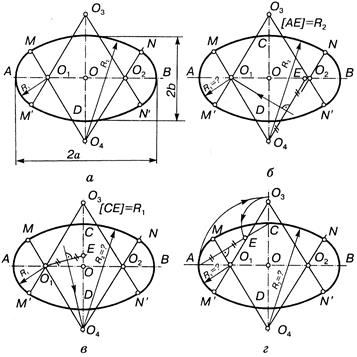
Построение овала по двум задан­ным осям АВ и CD (рис. 3.46). Ниже приведен один из множества вариантов решения. На верти­кальной оси откладываются отре­зок ОЕ, равный половине большой оси АВ. Из точки С как из центра проводят дугу радиусом СЕ до пе­ресечения с отрезком АС в точке Е₁. К середине отрезка АЕ₁ восстанавливают перпендикуляр и отмечают точки его пересечения с осями ова­ла O₁ и 0₂. Строят точки O₃ и 0₄, симметричные точкам O₁ и 0₂ от­носительно осей CD и АВ. Точки O₁ и 0₃ будут центрами опорных ок­ружностей радиуса R₁, равного от­резку О₁А, а точки O₂ и 0₄ — цент­рами дуг сопряжения радиуса R₂, равного отрезку О₂С. Прямые, со­единяющие центры O₁ и 0₃ с O₂ и 0₄ в пересечении с овалом опреде­лят точки сопряжения.

В AutoCAD построение овала производится с помощью двух опорных окружностей одинакового радиуса, которые:

1. имеют точку соприкосновения;

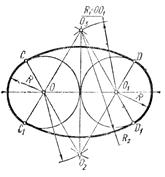
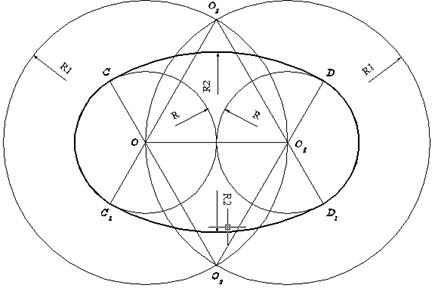
Рассмотрим первый случай. Строят отрезок OO₁=2R, параллельный оси Х, на его концах (точки О и О₁) размещают центры двух опорных окружностей радиуса R и центры двух вспомогательных окружностей радиуса R₁=2R. Из точек пересечения вспомогательных окружностей О₂ и О₃ строят дуги CD и C₁D₁ соответственно. Удаляют вспомогательные окружности, затем относительно дуг CD и C₁D₁ обрезают внутренние части опорных окружностей. На рисунке ъъъ полученный овал выделен толстой линией.

Рисунок Построение овала с соприкасающимися опорными окружностями одинакового радиуса

Источник