Что такое диагональ и как ее найти
Формулы и способы как находить диагональ квадрата
При решении задач по школьной математике часто требуется определить, чему равняется диагональ заданного квадрата. При кажущейся некоторой сложности, эта задача является весьма простой и имеет несколько несложных способов решения. Рассмотрим их, для начала введём некоторые понятия и определения.
Определения и соглашения
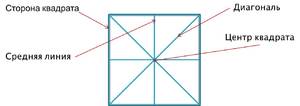
Как понятно из вышеизложенного, у квадрата только две диагонали. Поскольку квадрат является прямоугольником и сохраняет его свойства, то они равны между собой. Рассмотрим различные методы нахождения её длины.
Вычисление диагонали квадрата по известной стороне
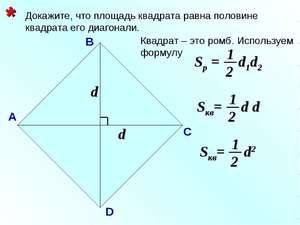
Самым простым способом является вычисление диагонали, если известна сторона квадрата. Здесь действует широко известная теорема Пифагора для прямоугольных треугольников. Запишем эту формулу: c^2 = a^2+b^2.
Отметим, что в нашем случае диагональ квадрата есть гипотенуза треугольника с равными катетами. Перепишем формулу исходя из наших условий: d^2 = a^2+a^2. Преобразуем, получим: d^2 = 2*a^2. Следующим шагом извлечём квадратный корень, получится: d = rad2*a. Это и есть наша конечная формула.
Рассмотрим вычисление на примере. Пусть a = 64. Подставим наше значение в формулу. Получим d = 64*rad2. Это и есть ответ.
Вычисление диагонали квадрата по известной площади
Пусть нам дана площадь квадрата, её обозначают латинской буквой S, найдём его диагональ.
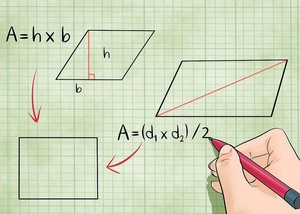
Используем свойства прямоугольника и запишем формулу его площади.
S = a*b. Перепишем для b = a. Получим: s = a^2. Отсюда найдём сторону: a = radS. Итак, нам удалось выразить сторону через площадь. Подставим полученное выражение в конечную формулу из предыдущей части. Формула примет вид: d = rad2*a = rad2*radS.
Пример: допустим, площадь равна 32 квадратных метра. Подставим это число. Получим rad2*rad32 = rad2*4*rad2 = 4*2 = 8 метров.
Вычисление диагонали по известному периметру
Пусть нам известен периметр. В дальнейшем его будем записывать латинской буквой P, найдём его d. Воспользуемся свойствами прямоугольника и запишем формулу его периметра.
P = два*(a + b). Перепишем для b = a. У нас получится: P = два*(a + a) = 2*2a = 4*a. Выразим из последней формулы сторону. Имеем: a = P/4. Воспользуемся тем, что: d = rad2*a. Выразим сторону через периметр. Наша формула примет видd = rad2*P/4.
Примере: пусть периметр равен 128 метров. Проведём несложный расчёт. Имеем, rad =d2*128/4 = 32*rad2 метров.
Вычисление по радиусу описанной и вписанной окружности
Ещё один способ, который на само деле очень простой. Радиус описанной окружности будем обозначать латинской буквой R, радиус вписанной окружности будем обозначать латинской буквой r.
Сначала разберёмся с описанной окружностью. В данной ситуации её радиус составляет ровно половину диагонали (это нетрудно убедиться с использованием построения), таким образом: R = 1/2*d. отсюда имеем: d = два*R. Снова поясним наши рассуждения на примере. Пусть R = 45 километров. Получим, d = два*45 = 90 километров.
И, наконец, рассмотрим метод, связанный с радиусом вписанной окружности. Опять-таки из построения чётко видно, что диаметр вписанной окружности равняется стороне квадрата. Таким образом, её радиус вдвое меньше стороны. Запишем это в виде формулы: r = 1/2*a. Отсюда следует, a = 2*r. Снова воспользуемся формулой из первого метода, подставим вместо стороны её выражение через радиус вписанной окружности. Выражение примет вид: d = rad2*a = rad2*2*r.
Ещё раз воспользуемся помощью примера. Пусть r = 98 метров. Тогда имеем, d = rad2*2*98 = 196*rad2.
Заключение
Таким образом, мы рассмотрели в статье пять принципиально различных методов вычисления диагонали квадрата. Если, на первый взгляд, задача казалась сложной, то после проведённых нами рассуждений стало очевидно, что особых проблем здесь нет. Сведём все полученные нами формулы в одну таблицу.
Хочется ещё отметить, что с помощью первой из наших формул очень легко построить отрезок, равный корню квадратному из двух. Для этого строим квадрат со стороной единица, его диагональ и будет равняться искомому отрезку.
Если на полученной диагонали мы построим прямоугольник, используя её как длину, а ширину возьмём равной единице, то получим отрезок равный ещё одному иррациональному числу корень квадратный из трёх.
Продолжая нашу цепочку и далее, мы научимся строить отрезки равные любому иррациональному числу.
Видео
Из видео вы узнаете, как найти диагональ квадрата, если известна его площадь.
Общая информация
В задачах по геометрии и физике приходится находить некоторые параметры прямоугольника: углы, стороны, периметр, площадь и диагонали. Все эти величины связаны между собой некоторыми соотношениями. Каждый должен уметь их рассчитывать, поскольку это необходимо не только для решения математических задач, но и в жизни. Например, при укладке керамзитной плитки на пол.
Используя свойство диагоналей, можно определить метод ее укладки. Кроме того, в физике иногда требуется рассчитать площадь поперечного сечения, а необходимая формула неизвестна. Во время планирования покупки строительных материалов нужно вычислить их количество, произведя вычисление площади или периметра помещения.
Однако формул для ведения расчетов недостаточно, поскольку нужно идентифицировать геометрическую фигуру. Для каждой из них применяются разные соотношения. В случае неверного определения вычисления окажутся недостоверными, а это негативно сказывается не только на экзаменах или контрольных, но и в финансовой сфере.
Сведения о прямоугольнике
Прямоугольником называется фигура с прямыми внутренними углами между смежными сторонами, у которой противоположные стороны равны. Его частным случаем, как говорят математики, является квадрат. У него все стороны равны, а углы также являются прямыми. Не каждый может правильно определить тип фигуры, поскольку от этого шага зависит правильность вычислений какого-либо параметра.
Для каждого геометрического тела существуют определенные критерии, по которым можно узнать его принадлежность. Эти критерии называются признаками. Некоторые новички путают признаки и свойства, но существует главное отличие, которое заключено в определении терминов «признак» и «свойство». Кроме того, специалисты предлагают простой способ, позволяющий избежать путаницы между терминами.
Идентификация или признаки
Признак — некоторые критерии, по которым можно отнести фигуру к определенному типу. Свойствами называются некоторые аксиомы и утверждения, полученные при доказательстве теорем. Идентифицировать прямоугольник можно с помощью теоремы из эвклидовой геометрии. Она имеет такую формулировку: если три угла фигуры являются прямыми, то она является прямоугольником. Для доказательства нужно выполнить такие действия:
Существуют также и другие признаки, по которым можно идентифицировать фигуру. По одному из них можно определить ее принадлежность к прямоугольнику. К признакам можно отнести такие:
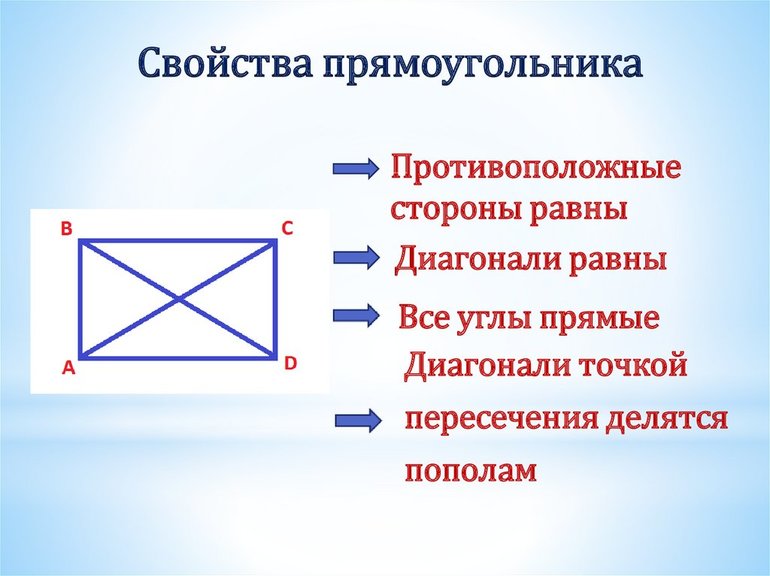
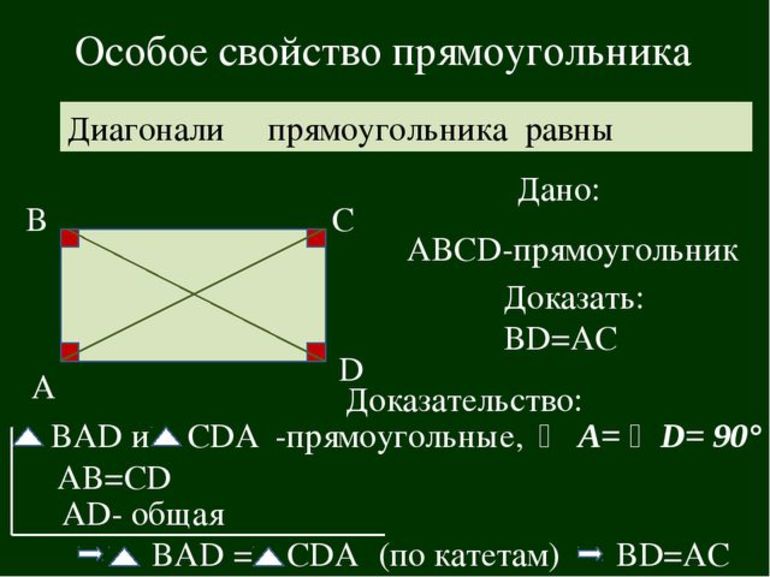
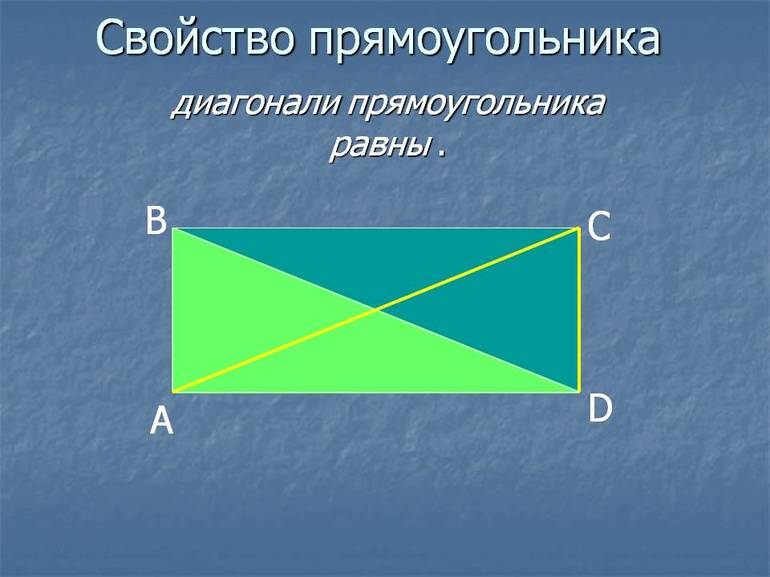
Первый и второй признаки получаются из основного определения фигуры. Третий признак является следствием доказательства теоремы, формулировка которой является следующей: диагонали прямоугольника равны. Она еще называется теоремой о диагоналях прямоугольника.
Для ее доказательства нужно начертить произвольный прямоугольник ABCD и провести в нем диагонали AC и BD. Они будут пересекаться в некоторой точке X. Они образуют прямоугольные треугольники ABC и ABD. В этом случае нужно доказать равенство треугольников. Они равны между собой: сторона АВ — общая, угол А равен В и сторона BC = AD (по равенству противоположных сторон). Из этого следует, что треугольники равны. Следовательно, их гипотенузы, которые также являются и диагоналями, равны.
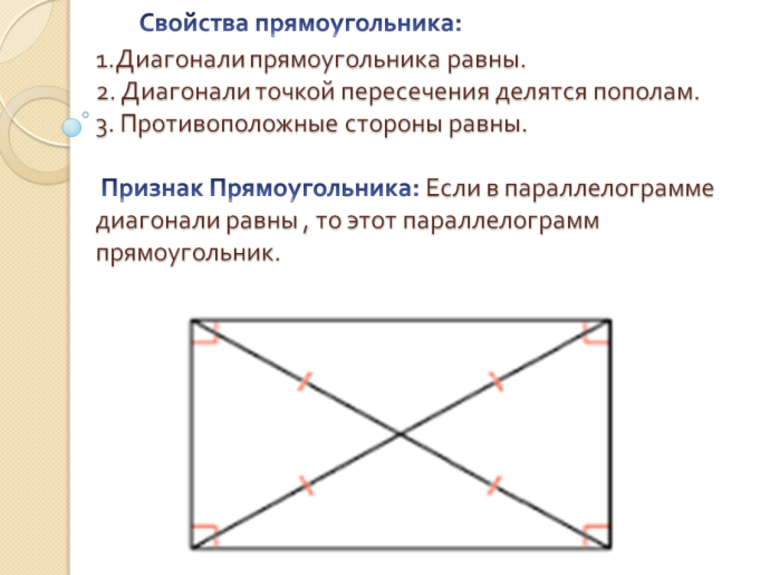
Свойства фигуры
Необходимо отметить, что квадрат — правильный четырехугольник, поскольку у него все стороны равны. Результирующая формула диагонали прямоугольника будет выглядеть таким образом: d = (AB 2 + BC 2 )^(½). При решении задач применяются свойства прямоугольника:
Однако при решении задач свойств недостаточно. Для этого применяются специальные соотношения и формулы. Некоторые из них были получены из свойств фигуры. Во всех формулах будет браться радиус описанной окружности — R и ее диаметр — D, а также функция «sqrt», которая эквивалентна квадратному корню (x^(1/2) = x^(0.5)).
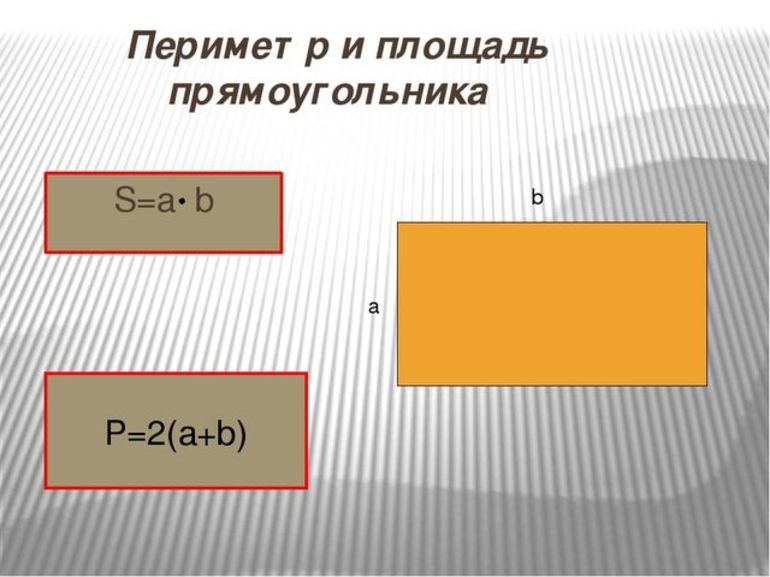
Периметр и площадь
Для удобства необходимо ввести некоторые обозначения. Диагонали следует обозначить литерой d, а противолежащие стороны — a и b, соответственно. Периметр — характеристика, соответствующая суммарному значению сторон фигуры. Очень часто ее обозначают литерой P. Существует также базовая формула: Р = 2а + 2b. Соотношение можно править таким способом: Р = 2 (a + b). Кроме того, существуют другие соотношения для определения P, когда известны некоторые параметры:
P и a (b): S = [(P * a) — 2a 2 ] / 2 = [(P * b) — 2b 2 ] / 2.
a (b) и d: S = a * sqrt[d 2 — a 2 ] = b * sqrt[d 2 — b 2 ].
Синус острого угла (Y) между двумя d и d: S = d 2 * sin (Y) / 2.
R и a (b): S = a * sqrt[4 * R 2 — a 2 ] = b * sqrt[4 * R 2 — b 2 ].
D и a (b): S = a * sqrt[D 2 — a 2 ] = b * sqrt[D 2 — b 2 ].
Для решения различных задач также могут быть полезны и другие соотношения, позволяющие найти не только диагонали, но и стороны прямоугольника.
Диагонали и стороны
Для оптимизации решения нужно знать формулы, с помощью которых можно находить одну из сторон или диагональ прямоугольника. Необходимо разобрать основные соотношения, по которым находятся стороны фигуры, когда известны следующие параметры:
Для нахождения диагонали также есть некоторые формулы. Для их применения следует знать такие параметры фигуры:
a и b: d = [a 2 + b 2 ]^(1/2).
S и a (b): d = (S 2 + a 4 )^(1/2) / a= (S 2 + b 4 )^(1/2) / b.
P и a (b): d = (P 2 — 4Pa + 8a 2 )^(1/2) / 2 = (P 2 — 4Pb + 8b 2 )^(1/2) / 2.
Однако это не все соотношения. В некоторых случаях разрешается описывать окружность вокруг фигуры. С помощью такого «геометрического хода» можно существенно упростить решение задачи. Это позволяет воспользоваться другими формулами.
Другие соотношения
Для решения задач используются и другие соотношения, которые позволяют найти параметры окружности, которая описана. Пусть дана окружность с радиусом R и диаметром D. Кроме того, известны некоторые параметры фигуры (a, b, d, P и S). С помощью формул можно найти D и R окружности при известных некоторых величинах:
a и b: R = (a 2 + b 2 )^(1/2) / 2.
P и a (b): R = (P 2 — 4Pa + 8a 2 )^(1/2) / 4 = (P 2 — 4Pb + 8b 2 )^(1/2) / 4.
S и a (b): R = (S 2 + a 4 )^(1/2) / 2a = (S 2 + b 4 )^(1/2) / 2b.
Пример решения
Пусть дана некоторая фигура, диагонали которой равны, а ее периметр равен 50. Одна из сторон a = 10. Следует провести идентификацию, а также найти такие параметры:
Данная задача является типом сложного класса, поскольку название фигуры не упоминается. Ее следует идентифицировать, а затем применить некоторые формулы для решения. Кроме того, необходимо верно выполнить 5 пункт. Однако не следует углубляться в строительную сферу. Бывают два метода укладки плитки: обычный — форма помещения является прямоугольником или квадратом, и с центра — другая фигура.
У фигуры диагонали равны, значит по третьему признаку она является прямоугольником. К нему можно применять вышеописанные формулы. Для нахождения другой стороны следует составить уравнение 2x + 2 * 10 = 50. Затем нужно перенести все известные значения в правую часть: 2х = 50 — 20. Далее можно найти переменную: х = 30 / 2 = 15 (ед.). Следует обратить внимание на написание единицы измерения. Если в условии задачи она не указана, то пишется единица измерения, которая заключается в круглые скобки. Достаточно найти только одну сторону, поскольку у прямоугольника существует свойство равенства противоположных сторон.
Значение диагоналей находится по формуле: d = [a 2 + b 2 ]^(1/2) = (15 2 + 10 2 )^(1/2) = (225 +100)^(1/2) = (325)^(1/2). Площадь можно найти таким образом: S = a * b = 15 * 10 = 150 [(ед.)^2]. Радиус вычисляется так:
R = (P 2 — 4Pa + 8a 2 )^(1/2) / 4 = (50 2 — 4 * 50 * 10 + 8 * 10 2 )^(1/2) / 4 = (1300)^(1/2) / 4 (ед.).
R = (S 2 + a 4 )^(1/2) / 2a = (150 2 + 100 4 )^(1/2) / (2 * 10) = (1300)^(1/2) / 4 (ед.).
Плитку можно укладывать обыкновенным способом, начиная не с центра, поскольку поверхность является прямоугольником. Все углы между сторонами равны между собой. Их градусная мера по 12 свойству соответствует 90.
Таким образом, при решении задач рекомендуется идентифицировать геометрическую фигуру, а затем применять к ней формулы.
Диагональ прямоугольника
Прямоугольник — четырёхугольник, у которого все углы равны 90 градусов, т. е. прямые.
Диагональ прямоугольника — прямая проложенная из противоположных вершин прямоугольника.
Диагонали прямоугольника равны и они делят прямоугольник на два равных прямоугольных треугольника.
Чтобы найти диагональ прямоугольника необходимо вспомнить теорему Пифагора, ведь диагональ — это гипотенуза прямоугольного треугольника, а стороны (длина и ширина) прямоугольника являются катетами треугольника.
Как найти диагональ прямоугольника
Воспользуемся теоремой Пифагора и формулой
d — диагональ квадрата
a — длина прямоугольника
b — ширина прямоугольника
Подставив в формулу вместо a длину прямоугольника, а вместо b — ширину прямоугольника и произведя расчет мы получим диагональ прямоугольника. Следует помнить, что у прямоугольника две диагонали и они равны между собой.
Диагональ прямоугольника онлайн калькулятор
Чтобы найти диагональ с помощью калькулятора введите длину и ширину прямоугольника и нажмите кнопку Рассчитать. В результате вы получите ответ и подробное решение.
Нахождение диагонали прямоугольника используется в различных жизненных ситуациях. К примеру, при проектировании фундамента дома необходимо проверить его диагонали — они должны быть равны между собой. Также на сайте можно рассчитать диагональ квадрата.
Как узнать размеры телевизора в сантиметрах: диагональ, ширина, высота
Самая популярная характеристика телевизора — диагональ в дюймах. Из нее можно узнать не только размер диагонали в сантиметрах, но и примерную ширину или высоту устройства.
Выбор телевизора — это очень непростая задача. Они отличаются друг от друга множеством характеристик. Это и разрешение, и яркость, и скорость работы матрицы, и, конечно, банальный дизайн. Но главная характеристика любого телевизора — это его диагональ, которая традиционно измеряется в дюймах.
Что такое дюйм? Сколько в нем сантиметров, и как понять, что телевизор с определенной диагональю поместится на отведенной ему тумбочке или нише. Не волнуйтесь, все проще, чем кажется, и сейчас мы в этом убедимся.
Сколько сантиметров в дюйме
Как известно, дюйм — это неметрическая единица измерения длины. Международная организация законодательной метрологии (МОЗМ) относит дюйм к тем единицам измерения, «которые должны быть изъяты из обращения как можно скорее. Тем не менее, все производители телевизоров, мониторов, смартфонов и другой техники продолжают активно использовать эту единицу измерения для описания размеров их экранов.
Поэтому при выборе телевизора просто необходимо уметь переводить дюймы в сантиметры. Благо, это сделать довольно просто. Достаточно знать лишь то, что в одном дюйме 2,54 см. А, зная это, вы легко поймете, что 43-дюймовый телевизор на самом деле имеет диагональ 109,22 сантиметра.
Сложности начинаются чуть позже. Что такое диагональ? Это расстояние от одного угла телевизора до противоположного. Но как это поможет нам понять, что телевизор поместится на тумбочке определенной длины или в нише с четко заданными длиной и шириной?
Как узнать длину и ширину телевизора по диагонали
Здесь нам может помочь знание обычной школьной программы. Любой школьник прекрасно знает теорему Пифагора: квадрат гипотенузы равен сумме квадратов катетов. А что такое телевизор? По сути это два одинаковых прямоугольных треугольника. Диагональ такого треугольника и будет диагональю телевизора, а прилежащие к ней катеты — это ни что иное, как его длина и высота.
Как измерить диагональ телевизора: нюансы при измерении
Сейчас в магазинах техники можно найти телевизоры на любой вкус и цвет.
Одной из главных характеристик, которой при рассматривании модели следует обязательно уделить внимания, является диагональ экрана.
Дело в том, что при замене устаревшего TV на новый нужно, чтобы покупка смогла уместиться в отведенное место.
Поэтому перед походом в магазин следует измерить диагональ телевизора.
Как померить диагональ телевизора
Разверните рулетку из одного угла экрана (его видимой области, корпус не учитывайте) в другой и старайтесь, чтобы лента была натянута по всей длине. Зафиксируйте стопором ленту и запишите измеренное значение. Если вы делали замеры ниткой — обрежьте ее по достижению пальца угла экрана и замерьте линейкой полученную длину.
Таким образом мы получили результат в сантиметрах и даже в милиметрах. А диагональ дисплеев, как принято во всем мире, измеряется в дюймах. Значит придется перевести сантиметры в дюймы. Возьмите ручку и приготовьтесь к растчету.
Один дюйм равен 2.54 сантиметра. Поэтому, полученный и записанный вами результат в сантиметрах нужно поделить на 2.54. К примеру, 82 см разделите на 2.54. Получится 32.28. Округляем в меньшую сторону, а значит диагональ вашего телевизора равна 32 дюйма.
На оставшийся хвостик можно не обращать внимание — производитель может не указывать точный размер экрана для упрощения оформления документации, или наоборот, как это принято в компьютерных мониторах, указать диагональ с десятыми, например, 24.3 дюйма или даже с сотыми, если речь идет об экране смартфона — 6.21 дюйм.
Способы измерения диагонали телевизора
Также найти эту информацию легко в интернете, достаточно вбить в поисковую строку модель устройства. Не редко производитель указывает данное расстояние на корпусе. Но нужно быть сконцентрированным, так как в такой ситуации число может быть как в сантиметрах, так и в дюймах.
Но бывают разные ситуации, когда необходимо самостоятельно померить диагональ телевизора. В таком варианте событий понадобится рулетка, можно воспользоваться линейкой, но в таком случае будут большие погрешности. Для измерения достаточно узнать дистанцию от левого нижнего угла до верхнего правого. Если необходимо посчитать измерения в дюймах, то полученное число следует поделить на 2.54.Некоторые телевизоры обладают выпуклым экраном. Из-за этого измерение диагонали телевизора рулеткой превращается в кошмар наяву. Чтобы избежать мучений, следует приготовить обычную длинную нитку. Один конец нужно приложить к левому нижнему углу, после чего протянуть к верхнему правому. Зафиксировать пальцем место «соединения» нитки и верхнего угла, затем замерить длину. Получившееся число и есть диагональ, только в сантиметрах.
Сложная геометрия
Измерить диагональ телевизора в см можно и простым школьным методом, зная длину и высоту видимой области экрана. Сам процесс измерения несколько проще, чем диагональ, т.к. вы имеете дело с реальными обхектами — горизонтальной и вертикальной прямой кромкой дисплея. Сделайте это с помощью рулетки или линейки. Причем, можно использовать и короткую линейку прикладывая ее последовательно, делая небольшие риски карандашом.
Итак, вы получили цифры по горизонтали, например, 75 и по вертикали 35. Квадраты этих чисел равны 5 625 и 1 225. Без калькулятора многим не обойтись ). А сумма квадратов равна 6 850. Остается только взять из нее корень. Получаем цифру 82,7 см. Делим ее на величину дюйма — 2.54 и получаем 32.58. Да, диагональ телевизора равна чуть более 32 дюйма.
Почему именно диагональ и почему именно в дюймах?
По первому вопросу есть две версии ответа. Первая звучит не очень правдоподобно, но имеет право существовать: у первых выпущенных телевизоров кинескопы выполнялись из круглой колбы. Но изображение ЭЛТ формировалось в виде прямоугольника. Соответственно, в характеристиках указывали диаметр кинескопа, который равнялся диагонали изображания.
Вторая версия более современная: соотношения сторон у дисплеев стандартные — 4:3 и 16:9. Поэтому для указания размера экрана телевизора достаточно было всего одной цифры вместо двух.
Но почему в дюймах? Справедливости ради стоит отметить, что на коробках современных телевизоров, поступающих в продажу в России, производитель указывает размер диагонали в сантиметрах. И это правильно. А дюмы указываются из-за того, что большую часть мониторов и смартфонов производят для международного рынка, а там распространена мера длины дюймы.
Важность выбора диагонали экрана телевизора
Вообще, диагональ, как и разрешение, влияет на четкость и качество картинки. Поэтому к выбору следует отнестись со всей серьезностью. Чем выше эти два параметра, тем лучше и живее будет картинка. Сейчас большинство производителей соблюдают это правило, но на рынке можно встретить TV, у которого диагональ большая, а разрешение низкое и наоборот.
Если в квартире небольшие комнаты, то рекомендуется покупать TV с большим разрешением. Так как при близком просмотре видны пиксели и другие недостатки видеоряда, а наблюдать плохое изображение – такой себе досуг. Вообще, идеальным считается то соотношение, при котором не видно пикселей.
Заключение
Диагональ телевизора – важная характеристика, определяющая качество и четкость видеоряда на экране. Измерить ее можно обычной рулеткой, используя правильные математические знания, как на фото выше. Еще более простой вариант – заглянуть в тех.паспорт устройства. Выбрать ее просто, если знать несколько не сложных правил. При этом нужно понимать важность правильного выбора.