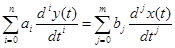Что такое диагностическая модель

диагностическая модель

3.7.16 диагностическая модель : Формализированное описание объекта, необходимое для решения задачи технического диагностирования.

Смотреть что такое «диагностическая модель» в других словарях:

диагностическая модель — Формализованное описание объекта, необходимое для решения задач диагностирования. Примечание Описание может быть представлено в аналитической, табличной, векторной, графической и других формах. В качестве диагностических моделей могут… … Справочник технического переводчика

СТО Газпром 2-2.3-141-2007: Энергохозяйство ОАО «Газпром». Термины и определения — Терминология СТО Газпром 2 2.3 141 2007: Энергохозяйство ОАО «Газпром». Термины и определения: 3.1.31 абонент энергоснабжающей организации : Потребитель электрической энергии (тепла), энергоустановки которого присоединены к сетям… … Словарь-справочник терминов нормативно-технической документации

диагностическое обеспечение — Комплекс взаимоувязанных правил, методов, алгоритмов и средств, необходимых для осуществления диагностирования на всех этапах жизненного цикла объекта. Диагностическое обеспечение объекта включает правила, методы, алгоритмы и средства… … Справочник технического переводчика

система — 4.48 система (system): Комбинация взаимодействующих элементов, организованных для достижения одной или нескольких поставленных целей. Примечание 1 Система может рассматриваться как продукт или предоставляемые им услуги. Примечание 2 На практике… … Словарь-справочник терминов нормативно-технической документации

Анализ временных рядов (time-series analysis) — А. в. р. наз. статистический анализ данных, собранных в ходе наблюдений за единичным объектом (напр., отдельным человеком, семьей или городом), производимых последовательно во времени, либо через определенные интервалы, либо непрерывно. Как и… … Психологическая энциклопедия

ТУБЕРКУЛЕЗ — ТУБЕРКУЛЕЗ. Содержание: I. Исторический очерк. 9 II. Возбудитель туберкулеза. 18 III. Патологическая анатомия. 34 IV. Статистика. 55 V. Социальное значение туберкулеза. 63 VІ.… … Большая медицинская энциклопедия

Шизофрения — У этого термина существуют и другие значения, см. Шизофрения (значения). Эта статья о психотическом расстройстве (или группе расстройств). О его стёртых формах см. шизотипическое расстройство; о расстройстве личности… … Википедия

Toyota Crown Majesta — Эта статья или раздел носит ярко выраженный рекламный характер. Это не соответствует правилам Википедии. Вы можете помочь проекту, исправив текст согласно стилистическим рекомендациям Википедии … Википедия

Шизофреник — Шизофрения Эйген Блейлер (1857–1939) впервые использовал термин «шизофрения» в 1908 г. МКБ 10 F20. МКБ 9 … Википедия

Игнатьев, Вячеслав Анатольевич — Вячеслав Анатольевич Игнатьев Дата рождения: 28 марта 1954(1954 03 28) (58 лет) Место рождения: Ленинград, СССР Страна … Википедия

Источник

Диагностические модели

Обеспечить требуемый уровень приспособленности объекта к диагностированию можно только в том случае, если уже с первого этапа его проектирования будут учитываться требования технической диагностики.

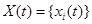
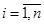
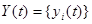
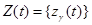
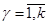
В общем случае под ОД понимается динамическая система (рис.15.1), y(t) преобразующая совокупность входных воздействий совокупность выходных реакций ,

Входные воздействия включают рабочие и тестовые сигналы, и помехи. Совокупность внутренних переменных , представляет собственные параметры объекта, определяющие его свойства как преобразователя Х(t) в Y(t), т.е. Y(t) = Z(t)Х(t).

Если зафиксировать входные воздействия в установленных пределах, то выходная реакция ОД должна быть в пределах области работоспособности в случае его работоспособного состояния. Если же при нормальном входном сигнале Y(t) выходит за установленные пределы, то произошли изменения свойств объекта, связанные с изменением Z(t).

Поскольку требуется выбрать диагностические признаки ОД, когда он еще физически отсутствует, то для этой цели приходится использовать его модель или модели. Под модельюобычно понимается упрощенный абстрактный или физический образ реального объекта (оригинала), подлежащего изучению. Следовательно, модель – приближенная копия оригинала, отображающая его определенные свойства, наиболее важные с точки зрения решаемой проблемы. На практике разрабатываются такие модели, которые представляют собой гомоморфный (частично соответствующий) образ объекта исследования и изоморфный (полностью соответствующий) образ его изучаемых свойств и характеристик.

Анализ объекта с целью определения его состояния предполагает построение математической модели. Теоретический анализ ОД при решении задач диагностирования предполагает некоторую идеализацию, которая абстрагирует подходящим образом выбранные существенные свойства объекта. Реальный объект при этом заменяется диагностической моделью (ДМ).

Оценка состояния ЭУ осуществляется по диагностическим признакам (параметрам и характеристикам). Обычно в качестве диагностических параметров принимаются параметры ДМ. В этом случае выбор или построение адекватной ДМ имеет существенное значение для оценивания состояния ЭУ.

В соответствии с ГОСТ 20911-89 диагностическая модель – формализованное описание объекта диагностирования, необходимое для решения задач диагностирования. Описание может быть представлено в аналитической, табличной, векторной, графической или другой форме.

ДМ в общем случае определяет зависимость выходных параметров (сигналов) объекта от его структурных (диагностических) параметров и входных сигналов. В некоторых случаях ДМ учитывают время.

ДМ могут иметь различный вид. Для описания ЭУ в основном применяются алгебраические уравнения (линейные и нелинейные), дифференциальные уравнения, передаточные функции, характеристические уравнения, графы и диаграммы прохождения сигналов, булевы функции.

Аппарат булевой алгебры, в основном, применяется для определения работоспособности и поиска дефектов в дискретных объектах. Такими объектами являются системы управления ЭУ, регулирования и защиты трансформаторов, электрических машин, воздушных линий, а также система контроля и проверки цепей релейной защиты автоматики.

В связи с большим разнообразием элементов ЭУ, как по назначению и режимам использования, так и по принципам построения и конструкции, разработчикам СД приходится использовать большое число различных ДМ. Чтобы облегчить выбор вида ДМ для конкретного оборудования на стадии его разработки, целесообразно классифицировать эти модели. Из всех возможных принципов построения системы классификации приведем классификацию диагностических моделей, основанную на методах их анализа. Такая классификация позволяет ориентировать разработчика при выборе ДМ на определенные методы их анализа и соответственно на использование конкретного математического аппарата.

По методам представления связей между состояниями объекта, его элементами и параметрами все ДМ, которые могут найти применение для описания электрооборудования, разбиваются на три группы: непрерывные, дискретные и специальные. Рассмотрим каждую из групп моделей отдельно.

Непрерывные диагностические модели. Непрерывными моделями оборудование проеставляют в том случае, когда рассматриваемые процессы протекают непрерывно или в непрерывно изменяющемся времени, которое является аргументом соответствующих функций. Такие модели объединяют линейные и нелинейные алгебраические и дифференциальные уравнения, передаточные функции и характеристические уравнения.

Алгебраически уравнения. Наиболее простыми ДМ являются линейные алгебраические уравнения, описывающие установившиеся (статические) процессы. Коэффициенты этих уравнений являются параметрами, характеризующими состояние объекта. В данном случае задача диагностирования сводится к оцениванию коэффициентов непосредственно или косвенно и сравнению с допустимыми значениями.

В общем случае такая модель записывается в виде:

где X – совокупность входных воздействий; Y – совокупность реакций ОД; A – оператор преобразования Х в Y;

, ; ; .

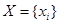
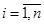
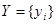
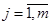
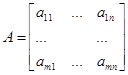
Если a_ij = const, то объект описывается линейными алгебраическими уравнениями, если a_ij = f(x), то объект описывается нелинейными уравнениями.

Собственно состояние объекта оценивает оператор А, структура и параметры которого определяют показатели качества работы объекта. При этом задачи контроля работоспособности и поиска дефектов решаются контролем соответствия действительного оператора А требуемому А_о.

В простейшем случае (рис.15.2) уравнение (15.1) имеет вид:

,

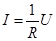
где 1/R = а – коэффициент уравнения.

Задача анализа таких моделей сводится к определению коэффициентов а_ij, которые являются прямыми диагностическими параметрами.

Дифференциальные уравнения. Наиболее широкое применение для описания процессов функционирования элект-рооборудования получили дифференциальные уравнения. Коэффициенты дифференциальных уравнений являются диагностическими параметрами. Они позволяют выявить дефекты, появляющиеся в динамических режимах. Задача диагностирования состоит в определении коэффициентов дифференциального уравнения (передаточных коэффициентов и постоянных времени) и сравнении их с допустимыми значениями.

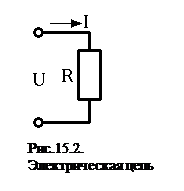
В общем виде такие ДМ для динамического объекта с одним входным воздействием х(t) и одним выходным сигналом y(t) имеют вид:

с некоторыми начальными условиями

, ,

где а_i, b_j – коэффициенты (прямые диагностические параметры) уравнений, m n + а_n-1р n-1 +. + а₁р + а_о = 0.

Решение такого уравнения позволяет определить коэффициенты (прямые диагностические признаки) через его корни. В зависимости от расположения полюсов – корней уравнения – определяется состояние ОД.

Линейная система устойчива по теореме Ляпунова, если полюса лежат в левой полуплоскости р₁, р₂ (рис.15.12), т.е. мнимая ось является границей устойчивости.

Если полюса расположены на мнимой оси (р₃,р₄), то в объекте существуют колебания (амплитуда колебаний постоянна, если полюса 1-го порядка). Полюса в правой полуплоскости (р₅,р₆) свидетельствуют об экспоненциальном нарастании колебаний и объект оказывается неустойчивым.

Следовательно, по расположению полюсов можно судить о работоспособности ОД.

Дискретные диагностические модели. Эти модели определяют состояние оборудования только для последовательности дискретных значений независимой переменной (времени), но без учета характера процесса в промежутках. Их можно представить конечно-разностными уравнениями или конечными автоматами.

Конечно-разностные уравнения. Такие уравнения связывают значения y_k (рис.15.13) функции y = f(x) на дискретном множестве значений x_k и записываются в общем виде:

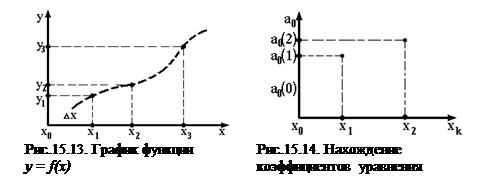y_k = f(y_k-1. y₁,x_k), k = 0,1,2,3.

Причем интервал 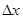между дискретными значениями x_k может быть постоянным или изменяться.

Обыкновенное разностное уравнение, используемое в качестве ДМ, имеет вид:

Если а_r = const,то уравнение линейное, если а_r = f(x_k),то – нелинейное. Как и в ранее рассмотренных ДМ коэффициенты а_r характеризуют изменение состояния ОД. Решить уравнение значит найти его коэффициенты.

Например, для r = 2 уравнение имеет вид:

Известны значения входной и выходной переменных в точках .

Источник

Оттиски и диагностические модели

Услуги по направлению

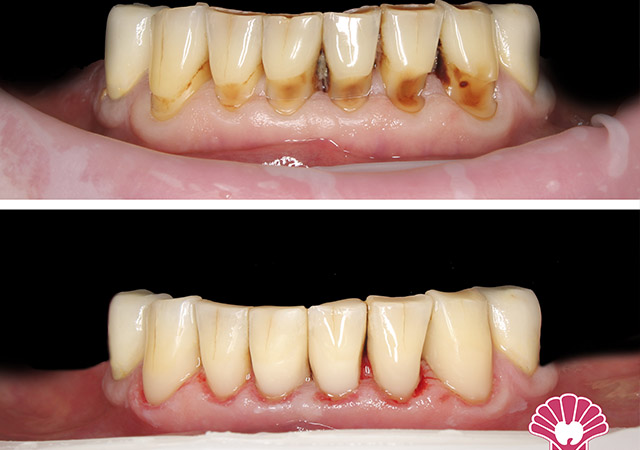
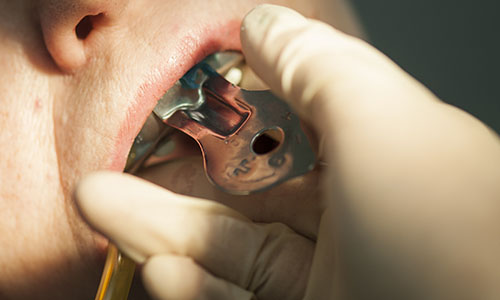
Диагностические модели представляют собой позитивное отображение зубного ряда и челюсти, а также тканей, слизистой, которая покрывает костный остов. Сделаны они по слепку из пластмассы или гипса. Для чего они нужны? Чтобы выявлять, в каком состоянии находятся зубы, какие изменения происходят с ними, проводить антропометрические измерения и решать многие другие задачи, после чего изготавливать качественные протезы или коронки.

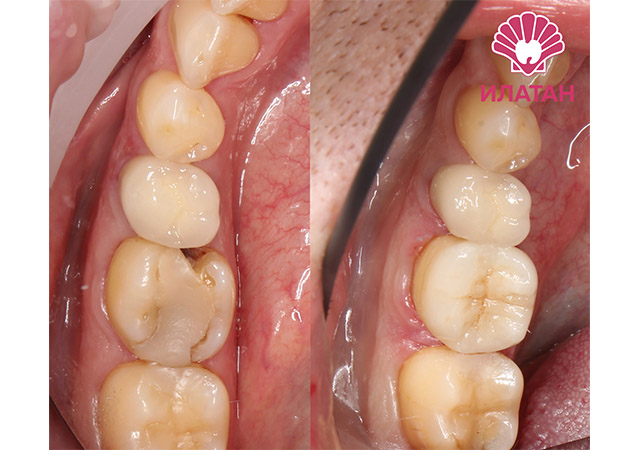
Клиники стоматологической сети «Илатан» приглашают пациентов на лечение зубов. У нас вы быстро и безболезненно решите имеющиеся проблемы – вылечите кариес, восстановите отсутствующие зубы, исправите некрасивый зубной ряд с помощью микропротезирования или ортодонтических техник.

Широкий спектр услуг стоматологического профиля позволяет нам позиционировать клиники «Илатан», как семейные стоматологии. С равным успехом мы восстанавливаем утраченные зубы возрастным пациентам, обеспечиваем идеальную улыбку молодежи, лечим зубы малышам – без боли и страха.

Награды, достижения, поздравления

Частые вопросы пациентов

Этот момент определяется на первичной консультации ортопеда. В зависимости от состояния зубов и от того, с какой целью пациент хочет поставить накладки, будет принято решение о необходимости препарирования эмали.

Композит – более хрупкий, чем современная керамика, например, накладки из E-Max. Поэтому нужно быть более аккуратным в процессе «эксплуатации» виниров из нанокомпозита. Однако стоимость установки композитных виниров ниже, чем у керамики.

Да, можно. Прямые композитные виниры, которые накладываются послойно, в большинстве случаев устанавливаются без обточки. Также можно избежать снятия эмалевого слоя и при фиксации на фронтальной поверхности зубов непрямых накладок.

Можно провести аппаратную чистку, она снимет слой налета, но кардинально изменить оттенок накладки или композитного материала, если они изменили цвет под воздействием пищевых красителей, не удастся.

Отзыв о работе доктора Владимира Арутюновича Чрагяна

Отзыв о стоматологии от Екатерины

Отзыв о лечение у главного врача Бердзенадзе Зураба Зауриевича

Диагностическая модель должна отвечать гарантировать четкое отображение:

Если, к примеру, какие-то зубы отломились или на них есть повреждения, их необходимо восстановить. После этого надо приклеить их к модели. Для этого нужно использовать цемент или клей. И соединить элементы, которые отломились или повредились, надо строго по линиям отлома. Кстати, надо иметь в виду, что самое тонкое место не должно быть менее десять миллиметров.

С помощью модели имеется возможность определить форму дуг, вид прикуса. Вот почему ее надо изготовить строго в соответствии со всеми требованиями. Неправильный прикус имеет большинство людей, и диагностические модели помогают выравнивать ряды. Они позволяют измерять ширину зубов и рядов, узнавать, в каком положении находятся зубы, которые ограничивают дефект (как наклонены, смещены и т.д.).

Чтобы контролировать процесс во время устранения патологий, применяют модели. Благодаря этому специалист видит, получается ли корректировать аномалии или нет, поэтому их еще называют контрольными.

Важно правильно снимать слепки, ведь именно по ним потом изготавливаются диагностические модели. От этого напрямую зависит успешность исправления прикуса и протезирования. С помощью моделей специалист делает измерения и производит расчеты. Исходя из полученных данных он решает, каким методом протезирования воспользоваться.

Только после того как врач изучает диагностическую модель и ставит диагноз, выбирается подходящее лечение. Доктор сообщает пациенту о том, какие возможные трудности его ждут. Если пациент согласен на лечение, специалист приступает к выполнению подготовительных мероприятий для проведения протезирования или ортодонтической процедуры.

Имейте в виду, что в процессе лечения несколько раз возникает необходимость делать слепки и создавать модели. Почему? Потому что специалистам нужно несколько раз убедиться, в правильном ли направлении они двигаются и есть ли анатомическое соответствие протезу. При необходимости лечение корректируется.

Что такое оттиск?

Оттиск — негативное отображение — нужен для создания моделей челюсти, которая в точности такая же, как и поверхность мягких и твердых тканей, находящихся на протезном ложе и его границах. Изготавливается из разных масс.

Оттиск снимается специальными приспособлениями — индивидуальной и стандартной ложкой. Если неправильно подобрать ее, качественно изготовить модель не получится. Поэтому важно учитывать особенности анатомии ротовой полости.

Рассмотрим стандартные ложки. Они бывают алпстмассовыми, металлическими или дюралюминиевыми. Такими ложками делают анатомические оттиски. А вот индивидуальными приспособлениями пользуются тогда, когда нужно сделать функциональные оттиски. И в этом случае учитывается, в каком состоянии находятся мягкие ткани в то время, когда человек говорит, глотает или пережевывает пищу. Обычно такое негативное отображение снимают с челюстей, у которых нет зубов.

Компрессионные оттиски получают с помощью материалов, отличающихся плотностью и вязкостью. А, используя текучие материалы, делают разгружающее негативное отображение. Во время его изготовления на ткань протезного ложа не должно оказываться давление.

Оттиски, состоящие из двух слоев (их еще называют двойными), снимать сложнее. Делается это в два этапа:

Источник

Общие сведения о диагностических моделях объектов

С целью использования математических методов анализа и оптимизации процесса получения информации о состоянии объекта и сокращения затрат на получение этой информации на этапе проектирования строится диагностическая модель объекта.

По методам представления взаимосвязей между состоянием объекта, его элементами и параметрами диагностические модели подразделяются на непрерывные, дискретные и гибридные.

Дискретные модели определяют состояние объектов для последовательности дискретных значений времени, как правило, без учета характера протекающих в промежутках процессов; эти модели представляются конечно-разностными уравнениями или конечными автоматами и используются для описания цифровых и импульсных устройств.

Гибридные модели описывают объекты, в состав которых входят как блоки непрерывного действия (аналоговые устройства), так и блоки преобразования дискретной информации (дискретные устройства).

По способам задания диагностические модели подразделяются на следующие группы:

· аналитические, выраженные явной математической зависимостью диагностических параметров от внутренних характеристик и параметров объекта;

· функциональные, представленные графическим или графоаналитическим описанием объекта посредством функционально связанных блоков или типовых элементов;

· логические, описанные логическими выражениями, например, средствами булевой алгебры, поведения и условий функционирования объектов, составленные с учетом входных воздействий и возможных вариантов состояний объекта;

· информационные, в которых состояние или процессы в объекте определяются методами теории информации.

Наибольшее распространение на практике получили аналитические, функциональные и логические модели объектов диагностирования.

Источник

II. Диагностические модели технических объектов

Технической диагностикой называется наука о распознавании состояния технической системы. Она изучает методы получения и оценки диагностической информации, диагностические модели и алгоритм принятия решения.

Целью технической диагностики является повышение надежности, безопасности и ресурса технических систем [3, с. 20].

Сущность диагностики машин состоит в разработке и практической реализации алгоритмов оценки параметров технического состояния объекта диагностирования без его разборки в рабочих условиях по контролируемым параметрам.

Технические системы состоят из большого числа взаимодействующих элементов, относительное перемещение которых порождает колебательные процессы, усиливающиеся или изменяющиеся при появлении дефектов.

В процессе превращения энергии источника в работу генерируются переменные силы, возбуждающие колебания. Эти колебания воспринимаются датчиками, и по ним делается заключение о состоянии механизма.

К задачам технической диагностики относятся, например, задачи связанные с определением срока службы объекта или с назначением периодичности его профилактических проверок и ремонтов. Эти задачи решаются путем определения возможных или вероятных эволюций состояния объекта, начинающихся в настоящий момент времени. Решение задач прогнозирования весьма важно, в частности, для организации технического обслуживания по состоянию (вместо обслуживания по срокам и по ресурсу).

Объект диагностирования (ОД) в технической диагностике – это такой технический объект, относительно которого решается определенная диагностическая задача.

В общем случае, диагностическая задача – это задача по установлению степени соответствия технического объекта предъявляемым к нему требованиям.

Принято различать две основные задачи: прямая диагностическая задача или задача контроля технического состояния и обратная диагностическая задача или задача поиска дефектов.

Исходя из этого, общее определение диагностической модели сформулируем в следующем виде.

Диагностическая модель – это любое знание, используемое в процессе решения диагностической задачи и представленное в определенной форме [3, с. 20].

Спектр форм диагностических моделей широк – от образов дефектов и их признаков в сознании отдельного специалиста-практика по обслуживанию и ремонту ОД до математических конструкций, реализованных в формальных диагностических программах.

Отметим, что прямая и обратная задачи являются по существу выражением в технической диагностике двух фундаментальных подходов теории систем.

Задача контроля есть выражение функционального подхода; задача поиска дефектов – выражение структурного подхода. Традиционно, используя готовый математический аппарат, для решения первой задачи применяют абстрактные модели (дифференциальное уравнение заданного порядка, аналитическое выражение логической функции, абстрактный конечный автомат), а для решения второй – структурные модели (структурные, комбинационные, последовательностные схемы).

Выбор диагностического сигнала должен проводиться таким образом, чтобы он был достаточно информативен для оценки вектора r, его изменений.

Сложность вибрационных процессов, вызванных работой технического объекта и его элементов, различие физических моделей и методов их математического описания на различных участках частотного диапазона послужили основанием для разбивки его на три поддиапазона: [2, с. 20]:

— диапазон низких частот (от 0 до 200-300 Гц);

— диапазон средних частот (от 200-300 Гц до 1-2 кГц);

— диапазон высоких частот (от 1-2 к Гц до 10-20 кГц).

При рассмотрении диагностических моделей целесообразно, на наш взгляд, ввести еще один поддиапазон: диапазон сверхвысоких частот (от 10-20 кГц до 100-200 кГц).

Полезность такого деления объясняется тем, что каждому диапазону свойственны свои возмущающие силы, своя физическая модель объекта как колебательной системы и своя диагностическая модель.

Низкочастотная вибрация носит преимущественно гармонический характер, так как одной из характерных причин ее является неуравновешенность вращающихся масс. Наиболее вероятными причинами низкочастотных колебаний являются: неуравновешенность, гарушение соосности валов; нарушение геометрии узлов; периодические силы, создаваемые рабочим процессом.

Динамическая модель механизма в области низкочастотных колебаний представляет собой комбинацию сосредоточенных масс, связанных с упругими безынерционными элементами. Силы в этих моделях обычно носят детерминированный характер. Весь объект рассматривается как единая упругая система, исследование которой производится методами прикладной теории колебаний.

Колебания среднечастотного диапазона обусловлены:

— высшими гармониками сил неуравновешенности элементов, обусловленных наличием нелинейных элементов в системе;

— нарушением геометрии кинематических пар;

— динамическим взаимодействием элементов машины между собой и с окружающей средой.

Каждая диагностическая модель имеет свои особенности.

Диагностический эксперимент или процесс диагностирования состоит из отдельных испытаний, которые принято называть элементарными проверками (ЭП).

Элементарная проверка есть акт однократной оценки определенного ДП. Оценка ДП производится в заранее фиксированных местах ОД, их принято называть контрольными точками (КТ). Часто ЭП называют пару, первая компонента которой – это определенное воздействие на ОД, а вторая – реакция ОД на это воздействие.

Ясно, что ОД, находящийся в разных технических состояниях (ТС), может выдавать разные реакции в одной и той же ЭП. При таком узком понимании ЭП можно различать три их вида.

Таким образом, всякий процесс диагностирования включает последовательности ЭП при известных условиях и заданном наборе КТ.

В рамках структурного подхода понятие ЭП применяют также к отдельным частям ОД или их совокупностям. В этом случае, предполагается доступность входов и выходов этих частей. Какова мощность множества возможных ЭП (ВМП).

Термин диагностическая модель можно понимать в широком и в узком смыслах. В первом случае это понятие включает в себя в достаточном объеме все три вида перечисленных выше знаний. Назовем такую диагностическую модель полной.

Автору не известны научные работы, в которых бы формально описывалась полная диагностическая модель. Хотя в практике диагностирования использование полных неформальных диагностических моделей – это норма. Пример этому дают инструкции по техническому обслуживанию ремонту сложных технических систем. В них обязательно есть раздел «возможные неисправности и методы их устранения», в котором, как правило, приводится таблица с перечнем дефектов, их диагностических показателей и методов их устранения.

В этой таблице сконцентрированы все три вида диагностических знаний. Кроме того, в инструкциях обычно точно сказано, с чего следует начать осмотр. Если обнаруживаются те или иные особенности функционирования ОД, то в инструкции сказано, какие дополнительные наблюдения или измерения необходимо сделать, какие профилактические мероприятия надо провести, или, наконец, указывается действие, устраняющее дефекты.

Другими словами, описываются алгоритмы диагностирования и ремонта. В результате субъект диагностической деятельности, реализующий указания инструкции, может и не знать, какова причина неисправности. Инструкция составляется обычно группой квалифицированных специалистов с учетом опыта эксплуатации таких же или подобных систем [3, с. 24].

Всякая диагностическая модель, формализующая процесс поиска, нужна для двух применений: для построения алгоритмов диагностирования и для построения эталонной модели.

При автоматизации процессов диагностирования алгоритм поиска дефектов служит основой для синтеза технических средств диагностирования, а эталонная модель является носителем исправного или технической неисправности в этих средствах.

Почему теоретическая диагностика до сих пор не имеет полных диагностических моделей? По-моему, одна из причин следующая. Взять готовый математический аппарат и применить его к ограниченной этим аппаратом диагностической задаче – такова сегодня традиция в теории диагностирования.

С другой стороны все три вида диагностических знаний не формализуются адекватно в рамках любого из существующих математических аппаратов.

Подобная ситуация имеет место и в других областях науки и практики [3, с. 25].

Альтернатива установившейся традиции – это сочетание формальных и неформальных методов анализа в рамках целостного единого процесса исследования. Реализация такого подхода возможна в развитии теории диагностических экспертных систем.

Модель, не содержащую в достаточном объеме, хотя бы один из видов диагностических знаний, будем называть частной диагностической моделью.

Приведем несколько примеров частных диагностических моделей.

Если перечислены идентификаторы возможных дефектов, допускается существование способа оценки вектора ДП, определены необходимые априорные вероятности, то для поиска может быть использована схема Байеса, согласно которой по наибольшему значению апостериорной вероятности принимается решение о текущем одиночном дефекте.

Таким образом, можно сделать вывод о том, что диагностические модели являются определенной разновидностью структурных математических моделей для решения сугубо прикладных, диагностических задач.

Источник