Что такое действующее значение тока или напряжения
Что такое действующее значение тока или напряжения
Переменным называется ток, который изменяется с течением времени:
Мгновенным значением переменного тока называется его значение в фиксированный момент времени.
Периодическим называют такой переменный ток, мгновенные значения которого повторяются через равные промежутки времени:
— период переменного тока, т.е. наименьший промежуток времени, по истечении которого мгновенные значения тока повторяются в той же последовательности.
Простейшим типом периодического тока является гармонический ток:
| где | — | амплитуда тока; |
| — | полная фаза колебания; | |
| — | начальная фаза колебания (при ); | |
| — | круговая частота (угловая скорость). |
Гармонический ток можно представить в виде проекции на вертикальную ось вращающегося вектора (рис.3.1).
Действующим или эффективным значением гармонического тока называется значение такого постоянного тока, который протекая через одно и тоже неизменное сопротивление за период времени выделяет такое же количество тепла, что и рассматриваемый гармонический ток.
Между амплитудным и действующим значением гармонического тока существует простая связь:
Аналогично для напряжения и ЭДС:
Для мгновенных значений достаточно медленно изменяющихся переменных ЭДС и токов справедливы основные законы постоянного тока в их наиболее общей форме.
Основными элементами электрической цепи переменного тока являются активное сопротивление, индуктивность и ёмкость.
Активное сопротивление представляет собой элемент электрической цепи, в котором при прохождении тока происходит необратимый процесс преобразования электрической энергии в тепловую.
Численное значение активного сопротивления определяется отношением мощности, расходуемой на тепло к квадрату действующего значения переменного тока:
Необходимо помнить, что
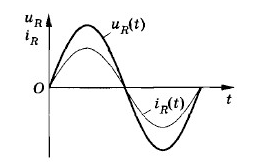
В цепи переменного тока с активным сопротивлением ток и напряжение совпадают по фазе (рис.3.2).
Тогда на основании закона Ома для участка цепи без ЭДС:
Подставляя (1) в (2) получим:
Разность фаз между напряжением и током:
В цепи с активным сопротивлением мгновенные, амплитудные и действующие значения напряжения и тока связаны законом Ома:
В цепи переменного тока с индуктивностью напряжение опережает по фазе ток на (рис.3.3). Покажем это.
При прохождении переменного тока в индуктивности возникает ЭДС самоиндукции:
На основании закона Ома для участка цепи с ЭДС можно записать:
Разность фаз между напряжением и током:
Таким образом, в цепи переменного тока с индуктивностью амплитудные и действующие значения напряжения и тока формально связаны законом Ома:
В цепи переменного тока с ёмкостью напряжение отстаёт по фазе от тока на угол (рис.3.4). Докажем это.
Это напряжение приложено к конденсатору от внешнего источника. Оно уравновешивает ЭДС ёмкости (аналогичную ЭДС самоиндукции в катушке индуктивности), которая возникает при наличии зарядов на обкладках конденсатора.
На основании закона Ома для участка цепи с ЭДС можно записать:
За положительное направление тока в соответствии с законом сохранения электрического заряда принимается направление, при котором заряды покидают обкладки конденсатора:
Разность фаз между напряжением и током:
Это расчётная величина, которая не имеет физического смысла.
В общем случае в состав цепи переменного тока могут входить и активное сопротивление, и ёмкость, и индуктивность. Все эти элементы могут быть соединены между собой как последовательно, так и параллельно. На рисунке 3.5 показана схема последовательного соединения указанных элементов и соответствующая им векторная диаграмма для тока и напряжений.
Падение напряжения на элементах цепи:
Приложенное мгновенное значение напряжения равно сумме мгновенных падений напряжения на отдельных элементах цепи:
Сложение этих гармонических напряжений произведено в векторной форме (рис.3.5). Порядок построения векторной диаграммы обозначен цифрами.
— активная составляющая напряжения.
— реактивная составляющая напряжения.
Из векторной диаграммы следует, что
— полное сопротивление цепи;
— активная составляющая сопротивления цепи;
— реактивная составляющая сопротивления цепи.
В зависимости от знака реактивного сопротивления треугольники напряжений могут иметь вид:
Угол положителен при отстающем и отрицателен при опережающем токе.
Если все стороны треугольников напряжений (рис.3.7) разделить на амплитуду тока, то получатся соответствующие треугольники сопротивлений (рис.3.8).
Из треугольников сопротивлений (рис.3.8) следует ряд важных соотношений:
| где | — | активное сопротивление катушки индуктивности; |
| — | активное сопротивление конденсатора; | |
| — | активное сопротивление внешнего резистора. |
Состояние электрической цепи на частоте носит название резонанса напряжений.
Работа в цепи переменного тока за время одного периода выражается формулой:
Средняя за период мощность называется активной мощностью:
Она расходуется в активном сопротивлении цепи переменного тока.
Наряду с изложенным необходимо иметь в виду, что любая реальная катушка индуктивности как и любой реальный конденсатор при работе в цепи переменного тока имеют не только реактивные, но и активные сопротивления. На рисунке3.9 показаны реальные катушка индуктивности и конденсатор и их эквивалентные схемы:
Эффективные (действующие) значения напряжения и силы тока.
В цепи переменного тока его направление и амплитуда меняются с частотой 50 Гц. Однако выделяемая на нагрузке энергия зависит не от направления тока в цепи, а лишь от его абсолютного значения. Всегда можно подобрать такое значение силы постоянного тока, чтобы энергия, выделяемая за некоторое время этим током на участке цепи с сопротивлением R, равнялась энергии, выделяемой за то же время переменным током.
Действующее значение силы переменного тока равно силе постоянного тока, выделяющего в проводнике то же количество теплоты, что и переменный ток за то же время. Оно определяется по формуле:

Действующее значение напряжения определяется аналогично:

Мощность, определяемая с использованием действующих значений силы тока и напряжения Р = IU, равна средней мощности переменного тока при совпадении фаз колебаний тока и напряжения:

Последнюю определяют усреднением мгновенной мощности за период колебаний:

Переменный электрический ток
теория по физике 🧲 колебания и волны
Свободные электромагнитные колебания в контуре быстро затухают. Поэтому они практически не используются. Наиболее важное практическое значение имеют незатухающие вынужденные колебания.
Переменный ток — вынужденные электромагнитные колебания.
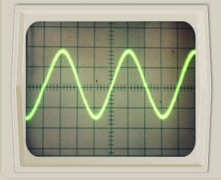
Ток в осветительной сети квартиры, ток, применяемый на заводах и фабриках, представляет собой переменный ток. В нем сила тока и напряжение изменяются со временем по гармоническому закону. Колебания легко обнаружить с помощью осциллографа. Если на вертикально отклоняющие пластины осциллографа подать напряжение от сети, то временная развертка на экране будет представлять сбой синусоиду:
Зная скорость движения луча в горизонтальном направлении (она определяется частотой пилообразного напряжения), можно определить частоту колебаний.
Частота переменного тока — это количество колебаний за 1 с.
Стандартная частота переменного промышленного тока составляет 50 Гц. Это значит, что на протяжении 1 секунды ток 50 раз течет в одну сторону и 50 раз — в другую. Частота 50 Гц принята для промышленного тока во многих странах мира. В США принята частота 60 Гц.
Если напряжение на концах цепи меняется по гармоническому закону, то напряженность электрического поля внутри проводника будет также меняться гармонически. Эти гармонические изменения напряженности поля вызовут гармонические колебания скорости упорядоченного движения заряженных частиц, и, следовательно, гармонические колебания силы тока.
При изменении напряжения на концах цепи электрическое поле не меняется мгновенно во всей цепи. Изменение поля происходит с большой скоростью, но она не бесконечно большая. Она равна скорости света (3∙10 8 м/с).
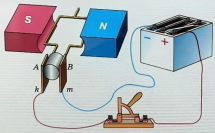
Переменное напряжение в гнездах розетки осветительной сети создается генераторами на электростанциях. Проволочную рамку, вращающуюся в постоянном однородном магнитном поле, можно рассматривать как простейшую модель генератора переменного тока (см. рисунок ниже).
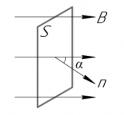
Поток магнитной индукции Ф, пронизывающий проволочную рамку площадью S, пропорционален косинусу угла α между нормалью к рамке и вектором магнитной индукции.
Численно магнитный поток определяется формулой:
При равномерном вращении рамки угол α увеличивается пропорционально времени:
где n — частота вращения. Поэтому поток магнитной индукции меняется гармонически:
Здесь множитель 2 π n представляет собой число колебаний магнитного потока за 2 π секунд. Это не что иное, как циклическая частота колебаний:
Согласно закону электромагнитной индукции ЭДС индукции в рамке равна взятой со знаком «минус» скорости изменения потока магнитной индукции, т.е. производной потока магнитной индукции по времени:
ε m a x — амплитуда ЭДС индукции, равная:
Напряжение в цепи переменного тока может меняться по закону синуса или по закону косинуса:
где U m a x — амплитуда напряжения (максимальное по модулю значение напряжения).
где I m a x — амплитуда силы тока (максимальное по модулю значение силы тока), φ с — разность (сдвиг) фаз между колебаниями силы тока и напряжения.
Пример №1. Найти напряжение в цепи переменного тока в момент времени t = π, если циклическая частота электромагнитных колебаний равна 300,25 Гц, а амплитуда напряжения составляет 12В. Считать, что напряжения меняется по закону косинуса.
Активное сопротивление в цепи переменного тока
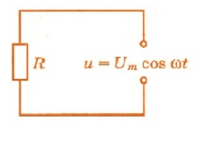
Пусть цепь состоит из соединительных проводов и нагрузки с малой индуктивностью и большим сопротивлением R (см. рисунок ниже).
Внимание! Ранее под величиной R мы понимали электрическое сопротивление. Но правильно его называть сопротивлением активным. Дело в том, что в цепи переменного тока могут быть сопротивления иного характера. Сопротивление же R называется активным, потому что при наличии нагрузки, обладающей этим сопротивлением, цепь поглощает энергию, поступающую от генератора. Эта энергия превращается во внутреннюю энергию проводников — они нагреваются.
Будем считать, что напряжение на зажимах цепи меняется по закону косинуса:
Для нахождения мгновенного значения силы тока мы можем воспользоваться законом Ома, так как эта величина прямо пропорционально мгновенному значению напряжения:
В проводнике с активным сопротивлением колебания силы тока по фазе совпадают с колебаниями напряжения, а амплитуда силы тока определяется равенством:
Мощность в цепи с резистором
В цепи переменного тока сила тока и напряжения меняются быстро, поэтому количество выделяемой энергии меняется так же быстро. Но заметить эти изменения невозможно. Чтобы найти среднюю мощность на участке цепи за много периодов, достаточно найти среднюю мощность за один период.
Средняя за период мощность переменного тока — отношение суммарной энергии, поступающей в цепь за период, к этому периоду.
Мощность постоянного тока определяется формулой:
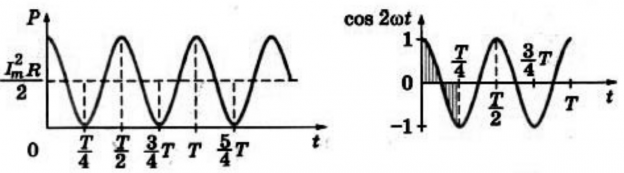
Следовательно, мгновенная мощность в цепи переменного тока на участке с активным сопротивлением R равна:
Подставим в это выражение полученное ранее значение мгновенной силы переменного тока и получим:
Вспомним из курса математики:
График зависимости мгновенной мощности от времени:
Средняя мощность − p равна:
Действующие значения силы тока и напряжения
Из предыдущей формулы видно, что среднее значение квадрата силы тока равно половине квадрата амплитуды силы переменного тока:
Действующее значение силы переменного тока — величина, равная квадратному корню, взятому из среднего значения квадрата тока. Обозначается как I.
I = √ − i 2 = I m a x √ 2
Смысл действующего значения силы переменного тока заключается в том, что оно равно силе постоянного тока, выделяющего в проводнике то же количество теплоты, что и переменный ток за это же время.
Аналогично определяется действующее значение напряжения U:
Именно действующие значения силы тока и напряжения определяют мощность P переменного тока:
Пример №3. Найти мощность переменного тока, если амплитуда силы тока равна 2 А, а сопротивление цепи равно 5 Ом.
Прописные истины для новичков.
Как рассчитать шунт для амперметра?
Почему, я намотал вторичную обмотку на 12 вольт, а блок питания у меня выдаёт 16 вольт?.
Как измерить, какую мощность выдаёт усилитель низкой частоты?
Такие вопросы порой часто возникают от новичков радиолюбителей. Кратко напомним им, чем нужно руководствоваться в своей практической деятельности.
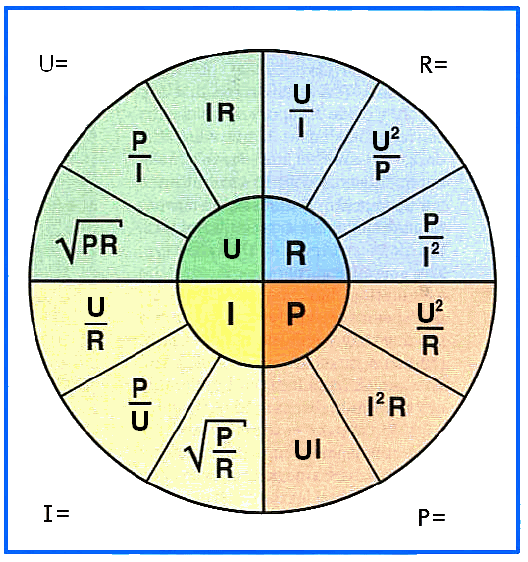
Закон Ома.
Количество теплоты, выделяемое в единицу времени в рассматриваемом участке цепи, пропорционально произведению квадрата силы тока на этом участке и сопротивлению участка.
В этом треугольнике Ома, нужно закрыть искомую величину, и два других символа дадут формулу для ее вычисления.
Закон Ома также применяется ко всей цепи, но в несколько изменённой форме:
Электрические измерения.
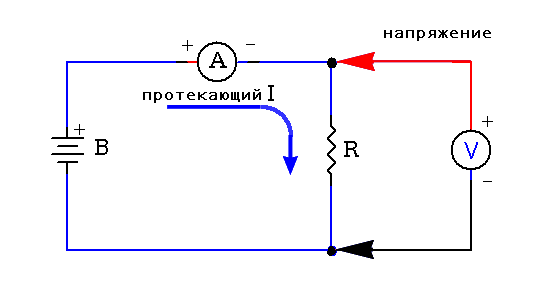
Нарисуем простейшую электрическую цепь, состоящую из батареи «В» и нагрузки «R», и рассмотрим, как необходимо измерять протекающий по цепи ток, и напряжение на нагрузке.
На рисунке выше показан порядок включения амперметра и вольтметра для измерения напряжения на нагрузке и протекающего через неё тока. Так же указана полярность подключения измерительных приборов в измеряемую цепь.
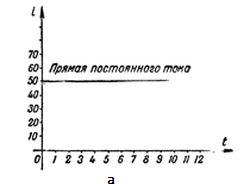
Постоянный и переменный ток.
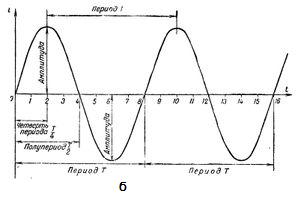
На рисунке выше, на графиках изображены диаграммы постоянного (а), и переменного (б) тока.
Промежуток времени, на протяжении которого совершается полный цикл изменения тока, называется периодом. Период обозначается буквой Т и измеряется в секундах.
Промежуток времени, на протяжении которого совершается половина полного цикла изменения тока, называется полупериодом. Следовательно, период изменения тока (ЭДС или напряжения) состоит из двух полупериодов. Совершенно очевидно, что все периоды одного и того же переменного тока равны между собой.
В течение одного периода своего изменения,ток дважды достигает максимального значения.
Максимальное значение переменного тока (ЭДС или напряжения) называется его амплитудой или амплитудным значением тока.
Действующее (эффективное) и амплитудное значение переменного синусоидального тока (напряжения).
Все электроизмерительные приборы (амперметры, вольтметры), отградуированы для измерения действующего значения синусоидального тока или напряжения.
Все конденсаторы в выпрямительных фильтрах соответственно заряжаются до величины амплитудного значения.
Можно посчитать, что при действующем напряжении сети 220 В, амплитудное его значение будет составлять 310 вольт (220 помножить на 1,41).
Отсюда вытекает, что если собрать выпрямитель переменного действующего напряжения 220 вольт, то конденсаторы фильтра необходимо применять на рабочее напряжение не менее чем на 350 вольт, так как они заряжаются до амплитудного (максимального) значения переменного напряжения, а ещё лучше не менее 400 вольт, для обеспечения надёжности работы выпрямителя.
Ответим на вопросы в начале статьи;
Параметры переменного напряжения
Как вы помните из предыдущей статьи, переменное напряжение — это напряжение, которое меняется со временем. Оно может меняться с каким-то периодом, а может быть хаотичным. Но не стоит также забывать, что и переменное напряжение обладает своими особенными параметрами.
Среднее значение напряжения
Среднее значение переменного напряжения Uср — это, грубо говоря, площадь под осциллограммой относительно нуля за какой-то промежуток времени. Чтобы это понять, давайте рассмотрим вот такую осциллограмму.
Например,чему равняется среднее значение напряжения за эти два полупериода? В данном случае ноль вольт. Почему так? Площади S1 и S2 равны. Но все дело в том, что площадь S2 берется со знаком «минус». А так как площади равны, то в сумме они дают ноль: S1+(-S2)=S1-S2=0. Для бесконечного по времени синусоидального сигнала среднее значение напряжения также равняется нулю.
То же самое касается и других сигналов, например, двухполярного меандра. Меандр — это прямоугольный сигнал, у которого длительности паузы и импульса равны. В этом случае его среднее напряжение также будет равняться нулю.
Средневыпрямленное значение напряжения
Чаще всего используют средневыпрямленное значение напряжения Uср. выпр. То есть площадь сигнала, которая «пробивает пол» берут не с отрицательным знаком, а с положительным.
средневыпрямленное значение напряжения будет уже равняться не нулю, а S1+S2=2S1=2S2. Здесь мы суммируем площади, независимо от того, с каким они знаком.
На практике средневыпрямленное значение напряжения получить легко, использовав диодный мост. После выпрямления синусоидального сигнала, график будет выглядеть вот так:
Для того, чтобы примерно узнать, чему равняется средневыпрямленное напряжение, достаточно узнать максимальную амплитуду синусоидального сигнала Umax и сосчитать ее по формуле:
Среднеквадратичное значение напряжения
Чаще всего используют среднеквадратичное значение напряжения или его еще по-другому называют действующим. В литературе обозначается просто буквой U. Чтобы его вычислить, тут уже простым графиком не отделаешься. Среднеквадратичное значение — это значение постоянного напряжения, который, проходя через нагрузку (скажем, лампу накаливания), выделяет за тот же промежуток времени такое же количество мощности, какое выделит в этой нагрузке переменное напряжение. В английском языке среднеквадратичное напряжение обозначается так: RMS (rms) — root mean square.
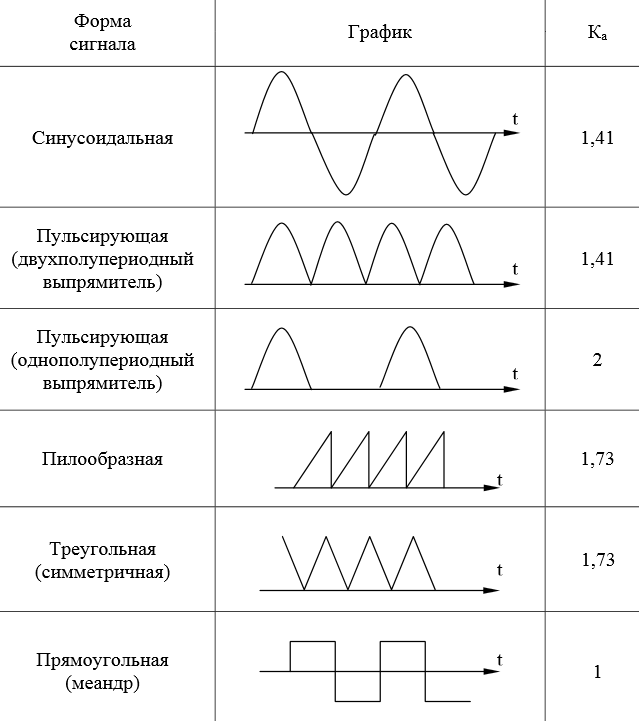
Связь между амплитудным и среднеквадратическим значением устанавливается через коэффициент амплитуды Ka:
Вот некоторые значения коэффициента амплитуды Ka для некоторых сигналов переменного напряжения:
Более точные значения 1,41 и 1,73 — это √2 и √3 соответственно.
Как измерить среднеквадратичное значение напряжения
Для правильного замера среднеквадратического значения напряжения у нас должен быть мультиметр с логотипом T-RMS. RMS — как вы уже знаете — это среднеквадратическое значение. А что за буква «T» впереди? Думаю, вы помните, как раньше была мода на одно словечко: «тру». «Она вся такая тру…», «Ты тру или не тру?» и тд. Тру (true) — с англ. правильный, верный.
Так вот, T-RMS расшифровывается как True RMS — «правильное среднеквадратическое значение». Мои токоизмерительные клещи могут замерять этот параметр без труда, так как на них есть логотип «T-RMS».

Проведем небольшой опыт. Давайте соберем вот такую схемку:
Выставим на моем китайском генераторе частоты треугольный сигнал с частотой, ну скажем, 100 Герц
генератор частоты
А вот осциллограмма этого сигнала. Внизу, в красной рамке, можно посмотреть его параметры

И теперь вопрос: чему будет равно среднеквадратическое напряжение этого сигнала?
Так как один квадратик у нас равняется 1 Вольт (мы это видим внизу осциллограммы в красной рамке), то получается, что амплитуда Umax этого треугольного сигнала равняется 4 Вольта. Для того, чтобы рассчитать среднеквадратическое напряжение, мы воспользуемся формулой:
Итак, смотрим нашу табличку и находим интересующий нас сигнал:
Для нас не важно, пробивает ли сигнал «пол» или нет, главное, чтобы сохранялась форма сигнала. Видим, что наш коэффициент амплитуды Ka= 1,73.
Подставляем его в формулу и вычисляем среднеквадратическое значение нашего треугольного сигнала
Проверяем нашим прибором, так ли оно на самом деле?
Супер! И в правду Тrue RMS.
Замеряем это же самое напряжение с помощью моего китайского мультиметра
Он меня обманул :-(. Он умеет измерять только среднеквадратическое значение синусоидального сигнала, а у нас сигнал треугольный.
Самый интересный сигнал в плане расчетов — это двуполярный меандр, ну тот есть тот, который «пробивает пол».
Его амплитудное Umax, средневыпрямленное Uср.выпр. и среднеквадратичное напряжение U равняется одному и тому же значению. В данном случае это 1 Вольт.
Вот вам небольшая картинка, чтобы не путаться
Так что же все-таки показывает мультиметр при измерении переменного напряжения? Показывает он НЕ амплитудное, НЕ среднее и НЕ среднее выпрямленное напряжение, а среднее квадратическое, то есть действующее напряжение! Об этом всегда помним.

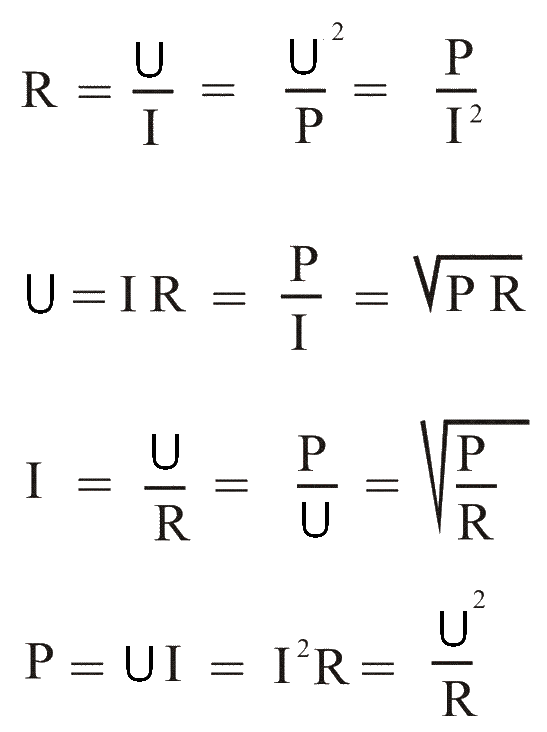




.png)


