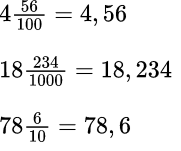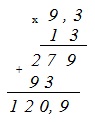Что такое десятичная дробь 5 класс правило с примерами
Десятичные дроби
Понятие десятичной дроби
Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.
Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которое можно представить число. Есть два формата записи:
В обыкновенной дроби над чертой принято писать делимое, которое становится числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление.
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. По сути, десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.
Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.
Свойства десятичных дробей
Главное свойство десятичной дроби звучит так: если к десятичной дроби справа приписать один или несколько нулей — ее величина не изменится. Это значит, что если в вашей дроби куча нулей — их можно просто отбросить. Например:
Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:
Обучение на курсах по математике — отличный способ закрепить полученные знания на практике и подтянуть сложные темы.
Как записать десятичную дробь
Давайте разберем на примерах, как записывается десятичная дробь. Небольшая напоминалка: сначала пишем целую часть, ставим запятую и после записываем числитель дробной части.
Пример 1. Перевести обыкновенную дробь 16/10 в десятичную.
Пример 2. Перевести 37/1000 в десятичную дробь.
Ответ: 37/1000 = 0,037.
Как читать десятичную дробь
Чтобы учитель вас правильно понял, важно читать десятичные дроби грамотно. Сначала произносим целую часть с добавлением слова «целых», а потом дробную с обозначением разряда — он зависит от количества цифр после запятой:
| Сколько цифр после запятой? | Читается, как |
|---|---|
| одна цифра — десятых; | 1,3 — одна целая, три десятых; |
| две цифры — сотых | 2,22 — две целых, двадцать две сотых; |
| три цифры — тысячных; | 23,885 — двадцать три целых, восемьсот восемьдесят пять тысячных; |
| четыре цифры — десятитысячных; | 0,5712 — ноль целых пять тысяч семьсот двенадцать десятитысячных; |
| и т.д. |
Сохраняй наглядную картинку, чтобы быстрее запомнить.
Преобразование десятичных дробей
Чтобы ни одна задача не смутила вас своей формулировкой, важно знать, как преобразовывать десятичные дроби в другие виды. Сейчас научимся!
Как перевести десятичную дробь в проценты
Уже в пятом классе задачки по математике намекают, что дроби как-то связаны с процентами. И это правда: процент — это одна сотая часть от любого числа, обозначают его значком %.
Чтобы узнать, как перевести проценты в дробь, нужно убрать знак % и разделить наше число на 100, как в примере выше.
А чтобы перевести десятичную дробь в проценты — умножаем дробь на 100 и добавляем знак %. Давайте на примере:
Выразить дробь в процентах просто: сначала превратим её в десятичную дробь, а потом применим предыдущее правило.
2/5 = 0,4
0,4 · 100% = 40%
8/25 = 0,32
0,32 · 100% = 32%
Чтобы разрезать торт на равные кусочки и не обижать гостей, нужно всего-то запомнить соотношения частей и целого. Наглядная табличка — наш друг-помощник:
Преобразование десятичных дробей
Десятичная дробь — это число с остатком, где остаток стоит после целой части и разделяется запятой.
Смешанная дробь — это тоже число с остатком, но остаток записывают в виде простой дроби (с черточкой).
Чтобы переводить десятичные дроби в смешанные, не нужно запоминать особые алгоритмы. Достаточно понимать определения и правильно читать заданную дробь — этим школьники и занимаются в 5 классе. А теперь давайте потренируемся!
Пример 1. Перевести 5,4 в смешанное число.
Пример 2. Перевести 4,005 в смешанное число.
Ответ: 4,005 = 4 1/200.
Пример 3. Перевести 5,60 в смешанное число.
Как перевести десятичную дробь в обыкновенную
Не будем придумывать велосипед и рассмотрим самый простой способ превращения десятичной дроби в обыкновенную. Вот, как это сделать:
Не забывайте про минус в ответе, если пример был про отрицательное число. Очень обидная ошибка!
Действия с десятичными дробями
С десятичными дробями можно производить те же действия, что и с любыми другими числами. Рассмотрим самые распространенные на простых примерах.
Как разделить десятичную дробь на натуральное число
Пример 2. Разделить 183,06 на 45.
Ответ: 183,06 : 45 = 4,068.
Как разделить десятичную дробь на обыкновенную
Чтобы разделить десятичную дробь на обыкновенную или смешанную, нужно представить десятичную дробь в виде обыкновенной, а смешанное число записать, как неправильную дробь.
Пример 1. Разделить 0,25 на 3/4.
Пример 2. Разделить 2,55 на 1 1/3.
Ответ: 2,55 : 1 1/3 = 1 73/80.
Как умножить десятичную дробь на обыкновенную
Чтобы умножить десятичную дробь на обыкновенную или смешанную, используют два правила за 6 класс. При первом приводим десятичную дробь к виду обыкновенной и потом умножаем на нужное число. Во втором случае приводим обыкновенную или смешанную дробь в десятичную и потом умножаем.
Пример 1. Умножить 2/5 на 0,8.
Пример 2. Умножить 0,28 на 6 1/4.
Ответ: 0,28 ∗ 6 1/4 = 0,8.
Как решать десятичные дроби 5 класс объяснение примеры
Для многих учеников десятичные дроби, как и действия с ними, вполне понятны. Но, есть и такие, которым трудно разобраться в данной теме. Чтобы помочь справиться с этой проблемой, учителям и родителям следует объяснить материал пятиклассникам в простой и доступной форме.
Понятие десятичной дроби 5 класс
Дроби, в написании которых, используют разделительную запятую, называют десятичными. Их особенность, знаменатель, являющийся степенью числа 10, т.е., это всегда единица с нулями. При чем, сначала пишут целую часть числа, затем — запятую, а после нее пишут дробную часть. Знаменатель нельзя увидеть в обычной форме записи, так как он «спрятан» за знаками после запятой.
Обычно, такие дроби пишут без знаменателя. При этом, отделяется запятой целая часть, а следом за запятой должно стоять такое количество цифр, сколько нулей в обычной дроби.
Деление и умножение на 10; 100; 0,1; 0,01 и т.д. только сдвигает запятую, но не меняет цифры.
Правила сравнения десятичных дробей
Прежде всего, необходимо понимать, что дробь 0,2 и дробь 0,20 друг другу равны. Нули, стоящие в конце десятичной дроби, величины ее не меняют и располагаться будут на координатном луче в одной точке. При сравнивании десятичных дробей, прежде всего сравниваются целые части, они расположены от запятой слева.
Например: 8,57 > 3,87, так как 8 > 3.
В случае, если равны целые части, сравнивают дробные.
На луче координат меньшие десятичные дроби находятся левее, так же, как натуральные числа:
0,2 Округление натуральных чисел 5 класс
Практически каждый день мы используем округление. Например, если от школы до дома расстояние — 602 метра, мы говорим, округляя значение, что это расстояние — 600 метров. Т.е., число 602 мы приблизили к числу 600, что воспринимается легче. Еще один пример — батон хлеба весит 397 грамм, округлив можно сказать, что батон весит 400 грамм.
Округление — это замена числа более приближенным и легким для восприятия.
В результате, при округлении, мы получаем «приближенное» число. Обозначается округление знаком ≈, который читается — приближенно равно (приблизительно).
Пример: 604≈600; 597≈600. Читается — шестьсот четыре приближенно равно шестистам и пятьсот девяносто семь приближенно равно шестистам.
Посмотрим еще примеры:
В примере мы видим округление до тысяч. Обратите внимание, что округление происходит в одном случае в большую сторону, а в другом в меньшую. Все числа после округления заменены на нули.
Правила округления десятичных дробей
Сложение вычитание десятичных дробей примеры
Чтобы найти разность или сумму 2-х чисел, следует выполнить такие действия:
Больше никаких действий предпринимать не надо. Как мы видим, складываются десятичные дроби, так же, как и обычные.
Главное в этих математических действиях — сопоставить правильно разряды слагаемых таким образом, чтобы десятичные точки были расположены друг под другом, на одной вертикале.
Необходимо придерживаться следующих правил:
Умножение и деление десятичных дробей 5 класс
Следует сказать, что эта тема для учеников 5-го класса совсем не сложная. Но, между тем, ученики часто допускают ошибки в правильной постановке запятой. Разберем подробнее, чтобы не допускались подобные ошибки.
При умножении, следуйте простому алгоритму:
Рассмотрим небольшой пример:
0,13*0,3 — после запятой количество знаков равно 3-м. Убираем запятые и выполняем умножение
запятую вернем обратно — 0,13*0,3=0,039
Обратите внимание — мы поставили 0, так как не хватило знака для правильной постановки запятой, перед числом. При этом, не пишут нули во множественном количестве, хотя их и можно поставить.
Теперь рассмотрим деление дробей по следующему алгоритму:
Если, у одного из чисел, не хватает части дробей, чтобы переместить запятую, добавьте нули. Например, если в числе 0,14 передвинуть на три знака, получится число — 140.
0,14:0,2 — число знаков наибольшее: 2, значит, запятую передвигаем и выполняем деление
Таким образом, на основе приведенных примеров, можно объяснить пятиклассникам простые математические действия с десятичными дробями.
Десятичные дроби
теория по математике 📈 числа и вычисления
Десятичная дробь — дробь, которая представляет собой способ представление числа в виде записи числа с запятой, где цифры перед запятой называются целой частью, а цифры после запятой – дробной частью (десятичной частью).
Десятичные дроби получают из записи обыкновенных дробей со знаменателем 10, 100, 1000 и так далее. Например, десятичные дроби:
4,56 – четыре целых пятьдесят шесть сотых 18,234 – восемнадцать целых двести тридцать четыре тысячных 78,6 – семьдесят восемь целых шесть десятых
Чтение десятичных дробей
Чтение десятичной части (десятых, сотых и так далее) зависит от количества цифр после запятой. Если цифра одна, то читают – десятых (в числе десять — один нуль, это соответствует одной цифре). Если две цифры после запятой, то читают – сотых (в сотне два нуля).
Десятичные дроби получаются из обыкновенных дробей:
Сложение (вычитание) десятичных дробей
Чтобы сложить (вычесть) в столбик две десятичные дроби нужно:
Если складывают (вычитают) целое число и десятичную дробь, то нужно поставить запятую после целого числа и приписать необходимое количество нулей после запятой.
Пример №1. Запись, где запятая под запятой и соответствующий разряд под соответствующим.
34,145 + 5,678 = 39,823
Пример №2. Запись, где также запятая под запятой, а во втором числе дописан нуль, чтобы уравнять количество знаков после запятой.
Пример №3. В первом слагаемом нет десятичной части, поэтому, после числа 56 поставили запятую и добавили нужное количество нулей.
Умножение десятичных дробей
При умножении двух десятичных дробей в столбик необходимо:
Пример №4. Запись выполнена так, что цифры по правому краю записаны ровно одна под одной, то есть как при обычном умножении чисел в столбик. Умножение выполнено без учета запятой. В ответе справа отделены 4 цифры запятой, так как в первом множителе их 3 после запятой, а во втором – одна, в двух множителях вместе – четыре.
0,125 × 2,3 00375 0250 0,2875
Пример №5. Здесь показано умножение десятичной дроби и целого числа. Умножение выполнено без учета запятой. В ответе отделена справа запятой только одна цифра, так как только в первом множителе есть десятичная часть с одной цифрой после запятой.
Умножение десятичных дробей на 10, 100, 1000…
Чтобы умножить десятичную дробь на 10, 100, 1000 и так далее, нужно перенести запятую вправо на столько цифр, сколько нулей у множителя. Умножение в данном случае выполняется в строчку.
Пример №6. 2,456 × 10 = 24,56 Запятую в десятичной дроби перенесли вправо на 1 цифру, так как у 10 один нуль.
Пример №7. 0,45678 × 100 = 45,678 Запятую перенесли вправо на 2 цифры, так как у 100 два нуля. Нуль, стоящий в начале десятичной дроби, убрали, так как впереди целой части, отличной от нуля он не пишется.
Пример №8. 9,46 × 1000 = 9460 в данном случае при переносе запятой на три цифра не хватило одной, поэтому в конце числа приписали нуль, и в ответе получилось целое число.
Умножение десятичной дроби на разрядную единицу 0,1; 0,01; 0,001…
При умножении десятичной дроби на разрядную единицу 0,1; 0,01; 0,001 (и так далее) нужно перенести запятую на столько цифр влево, сколько цифр в данной разрядной единице после запятой. Умножение обычно выполняется в строчку устно.
Пример №9. 983,7821 × 0,01= 9,837821 Переносим запятые влево на 2 цифры, так как в числе 0,01 две цифры после запятой.
Пример №10. 8,7654 × 0,1 = 0,87654 Перенесли на 1 цифру влево, так как в числе 0,1 одна цифра после запятой. В данном случае перед 8 появился нуль, так как при переносе запятой слева цифр не оказалось.
Пример №11. 7,98 × 0,0001 = 0,000798 При переносе влево на 4 цифры не хватило трех, поэтому впереди поставили нули, а также нуль образуется и в целой части.
Деление десятичных дробей
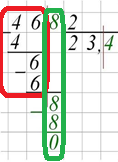
Пример №12. Деление десятичной дроби на целое число. 46,8 : 2 = 23,4
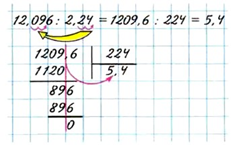
Пример №13. Деление десятичной дроби на десятичную дробь. 12,096 : 2,24 = 5,4 Из данного примера видно, что деление десятичных дробей обязательно сводится к делению на целое число.
Пример №14. 276,3 : 0,003 = 276300 : 3 = 92100. Здесь видно, что не хватает двух цифр в числе 276,3 и поэтому при переносе запятой к нему приписали два нуля. Затем выполнили деление двух целых чисел.
Деление десятичной дроби на 10, 100, 1000…
При делении десятичной дроби на 10,100, 1000 и так далее нужно перенести запятую на столько цифр влево, сколько нулей в данном числе. Деление выполняется в строчку устно.
Пример №16. 134,987 : 1000 = 0,134987 Перенесли запятую на три цифры влево, так как у 1000 три нуля. В целой части поставили нуль, так как цифр не хватило.
Пример №17. 7,234 : 100 = 0,07234 Перенесли запятую влево на две цифры. Так как цифр не хватало, то недостающие заменили нулями.
Деление десятичной дроби на разрядную единицу 0,1; 0,01; 0,001…
При делении десятичной дроби на разрядную единицу 0,1; 0,01; 0,001 и так далее нужно перенести запятую на столько цифр вправо, сколько цифр в данной разрядной единице после запятой. Деление обычно выполняется в строчку устно.
Пример №19. 41,234 : 0,01 = 4123,4 Перенос запятой на 2 цифры вправо, так как в числе 0,01 две цифры после запятой.
Пример №20. 56,91 : 0,001 = 56910 При переносе запятой на три цифры вправо приписали один нуль, так как одной цифры не хватило.
Сформируем из чисел ряд от наименьшего из них до наибольшего. Для этого сначала разделим их на положительные и отрицательные. И сразу получим наибольшее в ряду (поскольку оно единственное больше нуля): 0,021.
Три оставшихся отрицательных распределим по их модулям. Известно, что из двух отрицательных чисел больше то, у которого модуль меньше. Тогда получаем, что –0,304
pазбирался: Даниил Романович | обсудить разбор | оценить
Для получения результата необходимо последовательно выполнить математические действия в соответствии с их приоритетом.
Выполняем возведение в степень. Получаем числа, состоящие из единицы и следующего за ней количества нулей, равного показателю степени. При этом знаки «–» в скобках исчезают, поскольку показатели степеней четные. Получаем:
Выполняем умножение. Для этого в числе 0,3 переносим десятичную запятую на 4 знака вправо (так как в 10000 четыре нуля), а к 4 дописываем, соответственно, 2 нуля. Получаем:
Выполняем сложение –3000+400. Поскольку это числа с разными знаками, то вычитаем из большего модуля меньший и перед результатом ставим «–», поскольку число с большим модулем отрицательное. Получаем:
Так как оба числа отрицательные, то складываем их модули и перед результатом ставим «–». Получаем:
pазбирался: Даниил Романович | обсудить разбор | оценить
Это задание требует простого умения выполнять арифметические действия с десятичными дробями.
Сначала выполняем умножение. Умножаем –13 и –9,3 в столбик без учета знаков «–» перед сомножителями. В полученном произведении отделяем одну – последнюю – цифру десятичной запятой:
Знак произведения будет положительным, поскольку умножаются два отрицательных числа. Получаем:
Эту разность можно вычислить в столбик, но можно и устно. Выполним это действие в уме: вычитаем отдельно целые части и десятичные. Получаем:
pазбирался: Даниил Романович | обсудить разбор | оценить
Задачу можно решать разными путями, а именно менять последовательность действий, но этот вариант решения рекомендуется для тех, кто уверен в своих возможностях и знает математику на отлично. Для остальных мы рекомендуем выполнить последовательно действия в числителе и знаменателе, а затем разделить числитель на знаменатель. Числитель вычислять в данном примере нет необходимости, это число 9.
Вычислим значение знаменателя:
Можно произвести вычисления в столбик, тогда получим:
Либо перевести дробь к простому виду:
4,5 • 2,5 = 4½ • 2 ½ = 9 / 2 • 5 / 2 = 45 / 4
Последний случай предпочтительней, так как для дальнейшей операции — деления числителя на знаменатель задача упрощается. Делим числитель на знаменатель, умножая числитель на перевернутую дробь в знаменателе:
9 / ( 45 / 4 ) = ( 9 / 1 ) • ( 4 / 45 ) = ( 9 • 4 ) / (1 • 45 )
9 и 45 можно сократить на 9:
( 9 • 4 ) / (1 • 45 ) = ( 1 • 4 )/ (1 • 5 ) = 4 / 5 = 8 / 10 = 0,8
pазбирался: Даниил Романович | обсудить разбор | оценить
Повторение курса
1. Десятичная дробь – это форма записи обыкновенной дроби, у которой знаменатель равен 10, 100, 1000 и т.д.
Например, 1/100 = 0,01; 7/10 = 0,7 ; 19/1000 = 0,019
2. Запятая в десятичной дроби отделяет:
— целую часть от дробной;
— столько знаков, сколько нулей в знаменателе обыкновенной дроби.
3. Как перевести десятичную дробь в обыкновенную?
Запишите в числитель все число без запятой, а в знаменатель – единицу и столько нулей, столько цифр было отделено запятой в десятичной дроби.
4. Как обыкновенную дробь перевести в десятичную?
1 способ (хорошо работает, когда в знаменателе дроби: 2, 5, 20, 25… и т. д., то есть когда сразу понятно, на что надо умножать): домножить числитель и знаменатель дроби на такое число, чтобы в знаменателе получилось 10, 100, 1000 и т.д., а потом записать результат в десятичном виде.
2 способ: поделить числитель обыкновенной дроби на ее знаменатель (см. раздел сайта: 5 класс/десятичные дроби).
5. Сложение и вычитание десятичных дробей:
Сложение (вычитание) десятичных дробей выполняется так же, как сложение (вычитание) натуральных чисел, в столбик: главное, чтобы запятая во втором числе стояла под запятой в первом. Например:
6. Умножение десятичных дробей (см. раздел сайта: 5 класс/десятичные дроби/умножение десятичных дробей):
Чтобы перемножить две десятичные дроби, нужно умножить их как обычные числа, не обращая внимания на запятые. Потом сложить количество знаков после запятой в первом множителе и во втором множителе, а затем отделить полученное количество знаков в произведении, считая справа налево. Например:
7. Деление десятичных дробей (см. раздел сайта: 5 класс/десятичные дроби/деление десятичных дробей):
Чтобы разделить десятичную дробь на десятичную дробь, надо перенести запятую в делителе вправо на столько позиций, пока он не станет целым. Потом на столько же позиций перенести запятую в делимом. Затем разделить получившиеся числа как обычно, в столбик. При этом в ответе нужно будет не забыть поставить запятую сразу же, как мы «перейдем за запятую» в делимом. Например:
1. Вычислите:
2. Найдите значение выражения:
3. В летнем лагере за смену в 28 дней израсходовали 1 т картофеля. В первые 12 дней расход картофеля составил 38 кг в день. Каким будет расход картофеля в оставшиеся дни, если каждый день он будет одинаковым?
4. Найдите истинные высказывания. Расположите соответствующие им ответы в порядке возрастания, сопоставив их соответствующим буквам, и расшифруйте астрономический термин. Примеры, в которых допущена ошибка, решите правильно и запишите их в тетрадь.
Н 0,25 + 0,5 = 0,3 Б 0,5 * 3 = 0,15 Т 3,6 : 9 = 0,4
О 3,28 + 1,3 = 4,58 И 4 * 1,7 = 6,8 Я 12,3 : 5 = 24,6
Е=40,4 ; Д=36 ; С=8 ; Н=567 ; У=684,18 ; Л=636 ; Б=728 ; И=872.
7. Соком этого растения был отравлен король датский, отец Гамлета. Сейчас оно входит в состав мазей для лечения простуды, бронхита, плеврита, т. к. вещества, входящие в его состав, оказывают спазмолитическое действие. Что это за растение? (Результат каждого действия даёт букву.)
А=842,4 ; К=844,2 ; Е=23,2; С=93,5 ; Е=9,8 ; О=84,24 ; Н=82,124 ; Б=83,244 ; Л=39,244 ; Я=83,2.
8. Этого симпатичного зверька на латыни именовали «королём зелени». Назовите его:
Б=26 ; О=2,06 ; В=2,6 ; И=66,284 ; А=681,38 ; Л=9,08 ; А=9,8 ; Ц=98 ; Н=229,5 ; Е=0,3203 ; Р=22,95 ; К=32,03 ; К=30.
9. Выполните действия и округлите полученный результат с точностью: