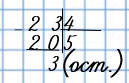Что такое деление с остатком 3 класс

Деление с остатком

Начнём рассмотрение новой темы с решения задачи.

Мама принесла 8 конфет и разделила их поровну между двумя детьми. Сколько конфет получил каждый?

Каждый ребёнок получил по 4 конфеты.

На следующий день мама опять принесла 8 конфет, но в гостях у её детей была ещё одна подружка. Мама опять разделила конфеты поровну, но уже между тремя детьми. Сколько конфет получил каждый ребёнок?

Каждый получил по 2 конфеты и 2 конфеты остались лишними.

Как сделать проверку?

Правило 1

Деление с остатком — это деление одного числа на другое, при котором остаток не равен нулю.

Правило 2

При делении с остатком остаток всегда должен быть меньше делителя.

Порядок решения

1. Нахожу наибольшее число до 14, которое делится на 5 без остатка. Это число 10.

2. Вычитаю из делимого найденное число: 14 − 10 = 4

3. Сравниваю остаток с делителем

Проверка деления с остатком

1. Умножаю неполное частное на делитель.

2. Прибавляю остаток к полученному результату.

3. Сравниваю полученный результат с делимым, он должен быть МЕНЬШЕ.

Деление в столбик

В 23 содержится 5 раз по 4, и ещё остаётся 3.

Решение записывают так:

23 : 4 = 5 (ост. 3) или так:

Поделись с друзьями в социальных сетях:

Источник

Математика. 3 класс

Конспект урока

Математика, 3 класс

Урок № 46. Деление с остатком

Перечень вопросов, рассматриваемых в теме:

1. Может ли при делении число не разделиться полностью?

2. В каких случаях выполняется деление с остатком?

3. Какое правило поможет научиться делить с остатком?

Деление – это обратное действие умножению.

Делимое – компонент деления, число которое делят.

Делитель – компонент деления, число на которое делят.

Частное – результат деления.

Неполное частное – результат деления с остатком.

Обязательная литература и дополнительная литература:

1. Моро М. И., Бантова М. А. и др. Математика 3 класс. Учебник для

общеобразовательных организаций М.; Просвещение, 2017. – с. 26.

2. Математика. 3 класс. Часть 2. / Л. Г. Петерсон – М.: Ювента, 2013 – с. 96.

Теоретический материал для самостоятельного изучения

Как узнать, сколько раз по три содержится в семнадцати? Разделим семнадцать на три. В семнадцати пять раз содержится по три и ещё останется два.

Два – это остаток. Число не разделилось полностью, поэтому частное называют неполное.

При делении с остатком можно пользоваться рисунком.

Рисунок может быть не всегда удобным. Записывать деление с остатком можно в столбик или как ещё называют уголком.

Рассмотрим пример. Семнадцать надо разделить на три.

При записи уголком неполное делимое пятнадцать пишем под числом семнадцать, а неполное частное под делителем. Это число пять. Из семнадцати вычитаем пятнадцать останется два. Это остаток.

При делении с остатком результат записывают двумя числами: неполное частное и остаток.

Выполним тренировочные задания.

№ 1. Вставьте пропущенные числа:

Ответ: 59 : 8 = 7 (ост.3)

№ 2. Соотнесите деление и результат.

Ответ: 24 : 5 = 4 (ост. 4)

«Троим детям раздали 7 пирожных. Сколько получилось у каждого и сколько осталось?».

№ 4. Выделите цветом, какой остаток может быть при делении на 4:

Источник

Деление чисел с остатком

Деление с остатком целых положительных чисел

Деление — это разбиение целого на равные части.

Остаток от деления — это число, которое образуется при делении с остатком. То есть то, что «влезло» и осталось, как хвостик.

Чтобы научиться делить числа с остатком, нужно усвоить некоторые правила. Начнем!

Все целые положительные числа являются натуральными. Поэтому деление целых чисел выполняется по всем правилам деления с остатком натуральных чисел.

Попрактикуемся в решении.

Пример

Разделить 14671 на 54.

Выполним деление столбиком:

Неполное частное равно 271, остаток — 37.

Ответ: 14671 : 54 = 271(остаток 37).

Деление с остатком положительного числа на целое отрицательное

Чтобы легко выполнить деление с остатком положительного числа на целое отрицательное, обратимся к правилу:

В результате деления целого положительного a на целое отрицательное b получаем число, которое противоположно результату от деления модулей чисел a на b. Тогда остаток равен остатку при делении |a| на |b|.

Неполное частное — это результат деления с остатком. Обычно в ответе записывают целое число и рядом остаток в скобках.

Это правило можно описать проще: делим два числа со знаком «плюс», а после подставляем «минус».

Все это значит, что «хвостик», который у нас остается, когда делим положительное число на отрицательное — всегда положительное число.

Алгоритм деления положительного числа на целое отрицательное (с остатком):

Пример

Разделить 17 на −5 с остатком.

Применим алгоритм деления с остатком целого положительного числа на целое отрицательное.

Разделим 17 на − 5 по модулю. Отсюда получим, что неполное частное равно 3, а остаток равен 2. Получим, что искомое число от деления 17 на − 5 = − 3 с остатком 2.

Ответ: 17 : (− 5) = −3 (остаток 2).

Деление с остатком целого отрицательного числа на целое положительное

Чтобы быстро разделить с остатком целое отрицательное число на целое положительное, тоже придумали правило:

Чтобы получить неполное частное с при делении целого отрицательного a на положительное b, нужно применить противоположное данному числу и вычесть из него 1. Тогда остаток d будет вычисляться по формуле:

d = a − b * c

Из правила делаем вывод, что при делении получается целое неотрицательное число.

Для точности решения применим алгоритм деления а на b с остатком:

Рассмотрим пример, где можно применить алгоритм.

Пример

Найти неполное частное и остаток от деления −17 на 5.

Разделим заданные числа по модулю.

Получаем, что при делении частное равно 3, а остаток 2.

Так как получили 3, противоположное ему −3.

Необходимо отнять единицу: −3 − 1 = −4.

Чтобы вычислить остаток, необходимо a = −17, b = 5, c = −4, тогда:

d = a − b * c = −17 − 5 * (−4) = −17 − (− 20) = −17 + 20 = 3.

Значит, неполным частным от деления является число −4 с остатком 3.

Ответ: (−17) : 5 = −4 (остаток 3).

Деление с остатком целых отрицательных чисел

Сформулируем правило деления с остатком целых отрицательных чисел:

Для получения неполного частного с от деления целого отрицательного числа a на целое отрицательное b, нужно произвести вычисления по модулю, после чего прибавить 1. Тогда можно произвести вычисления по формуле:

d = a − b * c

Из правила следует, что неполное частное от деления целых отрицательных чисел — положительное число.

Алгоритм деления с остатком целых отрицательных чисел:

Пример

Найти неполное частное и остаток при делении −17 на −5.

Применим алгоритм для деления с остатком.

Разделим числа по модулю. Получим, что неполное частное равно 3, а остаток равен 2.

Сложим неполное частное и 1: 3 + 1 = 4. Из этого следует, что неполное частное от деления заданных чисел равно 4.

Для вычисления остатка применим формулу. По условию a = −17, b = −5, c = 4, тогда получим d = a − b * c = −17 − (−5) * 4 = −17 − (−20) = −17 + 20 = 3.

Получилось, что остаток равен 3, а неполное частное равно 4.

Ответ: (−17) : (−5) = 4 (остаток 3).

Деление с остатком с помощью числового луча

Деление с остатком можно выполнить и на числовом луче.

Пример 1

Рассмотрим выражение: 10 : 3.

Отметим на числовом луче отрезки по 3 деления. Видим, что три деления помещаются полностью три раза и одно деление осталось.

Решение: 10 : 3 = 3 (остаток 1).

Пример 2

Рассмотрим выражение: 11 : 3.

Отметим на числовом луче отрезки по 3 деления. Видим, что три деления поместились три раза и два деления осталось.

Решение: 11 : 3 = 3 (остаток 2).

Проверка деления с остатком

Пока решаешь пример, бывает всякое: то в окно отвлекся, то друг позвонил. Чтобы убедиться в том, что все правильно, важно себя проверять. Особенно ученикам 5 класса, которые только начали проходить эту тему.

Формула деления с остатком

a = b * c + d,

где a — делимое, b — делитель, c — неполное частное, d — остаток.

Эту формулу можно использовать для проверки деления с остатком.

Пример

Рассмотрим выражение: 15 : 2 = 7 (остаток 1).

В этом выражении: 15 — это делимое, 2 — делитель, 7 — неполное частное, а 1 — остаток.

Чтобы убедиться в правильности ответа, нужно неполное частное умножить на делитель (или наоборот) и к полученному произведению прибавить остаток. Если в результате получится число, которое равно делимому, то деление с остатком выполнено верно. Вот так:

Теорема о делимости целых чисел с остатком

Если нам известно, что а — это делимое, тогда b — это делитель, с — неполное частное, d — остаток. И они между собой связаны. Эту связь можно описать через теорему о делимости с остатком и показать при помощи равенства.

Теорема

Любое целое число может быть представлено только через целое и отличное от нуля число b таким образом:

где q и r — это некоторые целые числа. При этом 0 ≤ r ≤ b.

Доказательство:

Если существуют два числа a и b, причем a делится на b без остатка, тогда из определения следует, что есть число q, и будет верно равенство a = b * q. Тогда равенство можно считать верным: a = b * q + r при r = 0.

Тогда необходимо взять q такое, чтобы данное неравенством b * q

Источник

Что такое деление с остатком: примеры для ребенка в 3, 4 классе

Как научить ребенка делению? Самый простой метод – выучить деление столбиком. Это гораздо проще, чем проводить вычисления в уме, помогает не запутаться, не «потерять» цифры и выработать мысленную схему, которая в дальнейшем будет срабатывать автоматически….

Как проводится

Деление с остатком – это способ, при котором число нельзя разделить ровно на несколько частей. В результате данного математического действия, помимо целой части, остается неделимый кусок.

Приведем простой пример того, как делить с остатком:

Есть банка на 5 литров воды и 2 банки по 2 литра. Когда из пяти литровой банки воду переливают в двухлитровые, в пятилитровой останется 1 литр не использованной воды. Это и есть остаток. В цифровом варианте это выглядит так:

5:2=2 ост (1). Откуда 1? 2х2=4, 5-4=1.

Теперь рассмотрим порядок деления в столбик с остатком. Это визуально облегчает процесс расчета и помогает не потерять числа.

Алгоритм определяет расположение всех элементов и последовательность действий, по которой совершается вычисление. В качестве примера, разделим 17 на 5.

Основные этапы:

Обратите внимание! При делении таким образом, остаток всегда должен быть меньше делителя.

Когда делитель больше делимого

Вызывают затруднение случаи, когда делитель получается больше делимого. Десятичные дроби в программе за 3 класс еще не изучаются, но, следуя логике, ответ надо записывать в виде дроби – в лучшем случае десятичной, в худшем – простой. Но (!) помимо программы, методику вычисления ограничивает поставленная задача: необходимо не разделить, а найти остаток! Дробная часть им не является! Как решить такую задачу?

Обратите внимание! Существует правило для случаев, когда делитель больше делимого: неполное частное равно 0, остаток равен делимому.

Как разделить число 5 на число 6, выделив остаток? Сколько 6-литровых банок влезет в пятилитровую? Ноль, потому что 6 больше 5.

По заданию необходимо заполнить 5 литров – не заполнено ни одного. Значит, остались все 5. Ответ: неполное частное = 0, остаток = 5.

Деление начинают изучать в третьем классе школы. К этому времени ученики уже должны освоить таблицу умножения, что позволяет им совершать деление двузначных чисел на однозначные.

Решите задачу: 18 конфет нужно раздать пятерым детям. Сколько конфет останется?

Примеры:

Находим неполное частное: 3*1=3, 3*2=6, 3*3=9, 3*4=12, 3*5=15. 5 – перебор. Возвращаемся к 4.

Остаток: 3*4=12, 14-12=2.

Ответ: неполное частное 4, осталось 2.

Вы можете спросить, почему при делении на 2, остаток либо равен 1, либо 0. По таблице умножения, между цифрами, кратными двум существует разница в единицу.

Еще одна задача: 3 пирожка надо разделить на двоих.

4 пирожка разделить на двоих.

5 пирожков разделить на двоих.

Это интересно! Изучение точного предмета: натуральные числа — это какие числа, примеры и свойства

Работа с многозначными числами

Программа за 4 класс предлагает более сложный процесс проведения деления с увеличением расчетных чисел. Если в третьем классе расчеты проводились на основе базовой таблицы умножения в пределах от 1 до 10, то четвероклассники вычисления проводят с многозначными числами более 100.

Данное действие удобнее всего выполнять в столбик, так как неполное частное также будет двузначным числом (в большинстве случаев), а алгоритм столбика облегчает вычисления и делает их более наглядными.

Разделим многозначные числа на двузначные: 386:25

Данный пример отличается от предыдущих количеством уровней расчета, хотя вычисления проводят по тому же принципу, что и ранее. Рассмотрим подробнее:

386 – делимое, 25 – делитель. Необходимо найти неполное частное и выделить остаток.

Первый уровень

Делитель – двузначное число. Делимое – трехзначное. Выделяем у делимого первые две левые цифры – это 38. Сравниваем их с делителем. 38 больше 25? Да, значит, 38 можно разделить на 25. Сколько целых 25 входит в 38?

25*1=25, 25*2=50. 50 больше 38, возвращаемся на один шаг назад.

Ответ – 1. Записываем единицу в зону не полного частного.

38-25=13. Записываем число 13 под чертой.

Второй уровень

13 больше 25? Нет – значит можно «опустить» цифру 6 вниз, дописав ее рядом с 13, справа. Получилось 136. 136 больше 25? Да – значит можно его вычесть. Сколько раз 25 поместиться в 136?

25*1=25, 25*2=50, 25*3=75, 25*4=100, 25*5=125, 256*=150. 150 больше 136 – возвращаемся назад на один шаг. Записываем цифру 5 в зону неполного частного, справа от единицы.

Вычисляем остаток:

136-125=11. Записываем под чертой. 11 больше 25? Нет – деление провести нельзя. У делимого остались цифры? Нет – делить больше нечего. Вычисления закончены.

Ответ: неполное частное равно 15, в остатке 11.

А если будет предложено такое деление, когда двузначный делитель больше первых двух цифр многозначного делимого? В таком случае, третья (четвертая, пятая и последующая) цифра делимого принимает участие в вычислениях сразу.

Приведем примеры на деление с трех- и четырехзначными числами:

75 – двузначное число. 386 – трехзначное. Сравниваем первые две цифры слева с делителем. 38 больше 75? Нет – деление провести нельзя. Берем все 3 цифры. 386 больше 75? Да – деление провести можно. Проводим вычисления.

75*1=75, 75*2=150, 75*3=225, 75*4=300, 75*5= 375, 75*6=450. 450 больше 386 – возвращаемся на шаг назад. Записываем 5 в зону неполного частного.

Находим остаток: 386-375=11. 11 больше 75? Нет. Еще остались цифры у делимого? Нет. Вычисления закончены.

Ответ: неполное частное = 5, в остатке 11.

Выполняем проверку: 11 больше 35? Нет – деление провести нельзя. Подставляем третье число – 119 больше 35? Да – действие провести можем.

35*1=35, 35*2=70, 35*3=105, 35*4=140. 140 больше 119 – возвращаемся на один шаг назад. Записываем 3 в зону неполного остатка.

Находим остаток: 119-105=14. 14 больше 35? Нет. Остались цифры у делимого? Нет. Вычисления закончены.

Ответ: неполное частное = 3, осталось 14.

Проверяем: 11 больше 99? Нет – подставляем еще одну цифру. 119 больше 99? Да – начинаем вычисления.

99*1=99, 99*2=198 – перебор. Записываем 1 в неполное частное.

Находим остаток: 119-99=20. 20&lt,99. Опускаем 5. 205&gt,99. Вычисляем.

99*1=99, 99*2=198, 99*3=297. Перебор. Записываем 2 в неполное частное.

Находим остаток: 205-198=7.

Ответ: неполное частное = 12, остаток 7.

Деление с остатком примеры

Учимся делить в столбик с остатком

Вывод

Таким образом проводятся вычисления. Если быть внимательным и выполнять правила, то ничего сложного здесь не будет. Каждый школьник может научиться считать столбиком, потому что это быстро и удобно.

Это интересно! Легкие правила округления чисел после запятой

Источник

Презентация «Деление с остатком» 3 класс

Описание презентации по отдельным слайдам:

Урок математики 3 «Б» класс по теме «Деление с остатком» Учитель начальных классов МБОУ Мирновская СОШ Лескова Марина Аркадьевна

Число ног у паука умножить на количество пальцев на руке у человека. «Весёлые примеры» 4. Тетрадь стоит 23 рубля. Сколько будут стоить 2 таких тетради? 2. Бабушке 54 года, а внук в 9 раз младше. Сколько лет внуку? 5. Половину рубля уменьшить в число хвостов у 10 котов. 3. Любимую оценку ученика умножить на самое маленькое двузначное число.

Тема урока «Деление чисел с остатком»

Можно ли 13 шариков разделить на 4? 13 : 4 = 3 (ост. 1) Я думаю нет!

Компоненты действия 13 : 4 = 3 (ост. 1) деления с остатком неполное частное остаток делимое делитель

ПРАВИЛО 1: При делении с остатком результат записывают двумя числами. Первое число называют неполным частным, второе – остатком. 13 : 4 = (ост. ) 3 1

Алгоритм деления с 13 : 4 = 3 (ост. 1) остатком Находим наибольшее число, (но меньше делимого), которое можно разделить на делитель без остатка. Данное число делим на делитель. Это значение частного. Оставшаяся часть делимого – это остаток. Проверяем, остаток должен быть меньше делителя.

2 0 4 При делении с остатком, подбирается наибольшее число до делимого, которое делится на делитель. 8 ост 4 2 : 5 =

Вариант 1 Вариант 2 Вариант 3 24:4=6 9:4=2(ост.1) 56:9=6(ост.2) 35:7=5 15:6=2(ост.3) 30:4=7(ост.2) 48:6=8 56:9=6(ост.2) 45:8=5(ост.5) 24:8=3 84:9=9(ост.3) 66:9=7(ост.3) 63:7=9 48:7=6(ост.6) 83:10=8(ост.3) 21:3=7

Задача В гости к бабушке пришли 4 внука. Бабушка решила угостить внуков конфетами. В вазочке было 23 конфеты. Сколько конфет достанется каждому внуку, если бабушка предложит поделить конфеты поровну? Решение: 23 : 4 = 5 (ост. 3) Ответ: 5 конфет достанется каждому внуку

Найди соответствие рисунка и записи 1 2 3 4 5 6 7 : 3 = 2 (ост.1) 10 : 4 = 2 (ост.2) 10: 3 = 3 (ост.1) 7 : 2 = 3 (ост.1) 5 : 2 = 2 (ост.1) 7 : 3 = 2 (ост.1)

Рефлексия Я на уроке научился… Я умею … Я могу научить других…

Строки от души… Какой был прекрасный сегодня … И много в душе родилось у нас… И ум наш в порядке, и есть у нас знанья. Теперь не страшны нам любые…

Строки от души… Какой был прекрасный сегодня урок! И много в душе родилось у нас строк. И ум наш в порядке, и есть у нас знанья Теперь не страшны нам любые заданья!

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Скоростное чтение

Курс повышения квалификации

Актуальные вопросы теории и методики преподавания в начальной школе в соответствии с ФГОС НОО

Ищем педагогов в команду «Инфоурок»

Номер материала: ДВ-571434

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Безлимитный доступ к занятиям с онлайн-репетиторами

Выгоднее, чем оплачивать каждое занятие отдельно

Путин поручил не считать выплаты за классное руководство в средней зарплате

Время чтения: 1 минута

Только каждый 10-й россиянин может дать платное образование своим детям

Время чтения: 2 минуты

Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст

Время чтения: 1 минута

В России утвердили квоты приема на целевое обучение в вузах на 2022 год

Время чтения: 3 минуты

ОНФ проверит качество охраны в российских школах

Время чтения: 2 минуты

ОНФ выявил за 2021 год более 600 опасных маршрутов к школам в регионах

Время чтения: 2 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник