Что может сделать волна

Интересные факты о волнах

Морей и океанов без волн, как известно, не бывает, даже в спокойную погоду водная масса непрерывно находится в движении и происходит вращение воды. В отличие от того времени, когда на Земле был только один океан Панталасса.

В океане шторма бушуют практически всегда, то в одной, то в другой его части. Зыбь от них преодолевает огромные расстояния, разбегаясь во все стороны, поэтому на океанские берега всегда обрушивается накат волн.

Что мы знаем об этом красивом явлении природы?

1. Волны способны путешествовать на невероятные расстояния: от шторма в Антарктике за две недели пересечь Тихий океан и дойти до Аляски.

2. Волны существуют как на поверхности, так и на глубине. Они носят название внутренних и могут возникать в морях, океанах и даже крупных озерах. Величина их достигает чудовищных размеров – до нескольких сотен метров в высоту и длину.

3. Цунами имеют столь разрушающую силу за счет невероятной скорости в 800 километров в час, как у современного пассажирского авиалайнера, стремительно обрушивая всю толщу воды — от самого дна до поверхности – на сушу. При этом гребни волн возле берега могут достигать всего лишь пять метров в высоту.

4. Древние греки обладали талантом «умасливать» непогоду, чтобы шторм не разрушил их суда. Мореплаватели выливали за борт несколько бочек рыбьего жира, тем самым уменьшая волны. Современные ученые нашли объяснение этому интересному факту: коэффициент поверхностного натяжения масляной пленки намного меньше, чем у воды, поэтому ветер поднимает не высокие волны, а всего лишь рябь.

5. В Солнечной системе не только на Земле рождаются волны. Выявили еще одно небесное тело – Титан, чья поверхность также имеет жидкость. Волны, пусть даже и полтора сантиметра высотой, были зарегистрированы в трех углеводородных морях этого спутника Сатурна: Море Кракена, Лигеи и Пунги.

6. Самая высокая волна покорилась человеку в 2011 году на португальском побережье. Американский серфер Гарретт Макнамар внес свое имя в Книгу рекордов Гиннесса, оседлав 24-метровый гребень. Но уже в 2013 году он сам же превзошел свой подвиг, прокатившись на 30-метровой волне.

7. Не только людям нравится кататься на волнах, с 1920-х годов существует такой необычный вид спорта, как собачий серфинг. Он родился на берегах Калифорнии и с 2006 года проводит свои соревнования на регулярной основе. У него даже есть свой абсолютный чемпион. Золотистый ретривер Рикошет (смотрите милейшую подборку о 10 породах собак, которые были выведены случайно) не только лихо рассекает по волнам, но и учит серфингу больных детей и людей с ограниченными возможностями.

Источник

Разбираемся в физике частиц: 3) волны, классический вид

Разобравшись с уравнениями для колебаний – описывающими практически всё, что скачет, вибрирует, катается вперёд-назад, как шар на пружине – можно переходить к настолько же распространённому явлению природы, волнам. Волны есть везде: звук и свет, землетрясения, рябь на поверхности пруда, и т.п.

Но перед этим предупреждаю, что термин «волна» может вводить в заблуждение, поскольку в физике он означает не то же самое, что в английском языке. В физике он не означает того, что мы обычно могли бы назвать волной на краю океана – один гребень и одна впадина. В физике волны – это последовательность волн, несколько гребней и впадин, совместно движущихся в одном направлении. У волны простейшего вида все гребни одинаковой высоты и отстоят друг от друга на одно расстояние. Мы будем рассматривать именно такой случай.

Волны – выдающееся явление, если задуматься. Представьте, что вы с другом взяли длинную верёвку и туго натянули её в комнате (рис. 2). Затем представьте, что ваш друг поболтал несколько раз вверх и вниз одним концом верёвки (зелёным). На его конце верёвки появится волна, и она пройдёт по комнате к вашему концу верёвки (красному).

Это удивительно. Я имею в виду – на самом деле поразительно, сильно и критически важно для всего в нашей Вселенной, включая и вас лично. Посмотрите, что произошло. Ни один физический объект слева направо не перемещался – до того, как ваш друг начал двигать конец верёвки, она была протянута через комнату, а в конце, после того, как ваш конец верёвки закончит колебаться и волна пропадёт, верёвка так и останется натянутой через всю комнату, как и было. И всё-таки! Энергия и информация переместились по комнате. Волна в пути переносит энергию, потраченную вашим другом на колебания верёвки – и несёт в своей форме информацию о том, сколько раз и как быстро он её дёргал – к вам, где она заставляет трястись уже вашу руку. И в этом случае она даже тряханёт вашу руку именно столько раз и именно в такой последовательности. Вот это да! Ни один физический объект не перемещался через комнату, а энергия и информация – переместились.

Или, подождите. А не должны ли мы рассматривать волну, как физический объект? Такой же физический, как сама верёвка?

Помня этот глубочайший вопрос, обратимся к небольшому количеству математических формул, необходимых для описания внешнего вида и поведения волны, а затем используем чуть больше математики, чтобы записать уравнения, решениями которых будут волны. Это похоже на то, что мы делали для классического шара на пружине.

Формула для бесконечной волны в определённый момент времени

Эта серия статей сразу после шара на пружине переходит к волнам потому, что волна – это разновидность двойного осциллятора. Она колеблется как во времени, так и в пространстве. Время мы обозначим буквой «t», а пространство – «x».

Обратите внимание на рис. 3. На нём изображена волна, простирающаяся в обоих направлениях на большое расстояние, на которой уместилось множество гребней и впадин. Это отличается от волны на рис. 2, у которой всего несколько гребней и впадин. Но это различие не имеет отношения к делу – на рис. 2 мне нужно был проиллюстрировать то, для чего не имела значения точная форма волны; теперь же мы сконцентрируемся на математической формуле для волн, а это гораздо проще сделать, если у волны есть большое количество гребней и впадин одинакового размера. Также этот случай окажется очень полезным для понимания того, как квантовая механика влияет поведение волн.

Рис. 3

Сначала нам нужно определиться с обозначениями и записать формулу, описывающую движение и форму волны на рис. 3, как мы делали для шара на пружине.

На графике показана величина волны Z как функция от пространства в определённый период времени t = t₀ — мы записываем это, как Z(x, t₀). Отслеживая волну в пространстве мы видим, что она колеблется вперёд и назад, и Z периодически увеличивается и уменьшается. В любой момент времени волна колеблется в пространстве.

Заметьте, что Z не обязательно должна быть связана с физическим расстоянием. Это может быть высота верёвки, как на рис. 2, или это может быть нечто совсем другое, к примеру, температура воздуха в определённой точке пространства и времени или ориентация магнитного атома в определённом месте магнита. Но x всё же представляет физическое расстояние, а t – время.

У снимка этой волны, Z(x, t₀), есть три интересных свойства, два из которых также относятся и к шару на пружине.

1. Существует значение равновесия Z₀, лежащее посередине между самым большим значением Z на гребне и самым малым значением Z во впадине. Большую часть времени мы изучаем волны, у которых Z₀ = 0, поскольку часто величина Z₀ не имеет значения – но не всегда.
2. У волны есть амплитуда А, величина, на которую меняется Z от равновесного значения до вершины каждого гребня или на ту же величину до дна каждой впадины.
3. У волны есть длина – расстояние λ между соседними гребнями, или, что то же самое, между соседними впадинами, или, что то же самое, удвоенное расстояние между соседними гребнем и впадиной. Она описывает колебания в пространстве так же, как период (равный 1/частоту) описывает колебание во времени шара на пружине.

Рис. 4

Что же напоминает нам форма на рис. 3? Она выглядит, как график функции синуса или косинуса – см. рис. 4, где cos(w) построен на графике по w. Cos(w) – функция осциллирующая, у которой есть очевидная позиция равновесия в нуле, её амплитуда 1, а длина волны — 2π. Как перейти от рис. 4 к формуле для волны на рис. 3? Сначала мы умножим cos(w) на А, чтобы амплитуда сравнялась с А. Затем мы добавим Z₀ ко всей формуле, чтобы сдвинуть её до нужного значения равновесия (если А = 0, то колебаний нет, и всё покоится в точке Z = Z₀). И, наконец, заменим w на 2πx/λ, поскольку у cos(w) гребни на w = 0 и w = 2 π, поэтому у cos(2πx/λ) гребни будут на x = 0 и x = λ. Всё вместе это даёт нам

Это практически та же формула, что описывала движение шара на пружине во времени:

Где ν – частота колебаний, а T = 1/ν – период колебаний. Видите аналогию: период относится ко времени, как длина волны к пространству.

Ещё одно замечание до того, как мы продолжим. Я мог записать также:

Поскольку cos[w] = cos[-w]. То, что мы спокойно можем подставить минус в формулу формы волны, будет важно позднее.

Формула для бесконечной волны в определённом месте

Рис. 5

Теперь зададим другой вопрос: посмотрим, как волна меняется во времени, отслеживая определённую точку на верёвке, и увидим, как она себя ведёт и двигается. Это показано на рис. 5: там я обозначил определённую точку x₀, которая в момент времени t₀ находится на гребне. Волна двигается вправо и следует размеру волны Z в точке x₀, меняясь во времени: Z(x₀, t). И вы немедленно увидите, что высота волны в определённой точке ведёт себя точно так же, как шар на пружине! Поэтому у неё будет точно такая же формула, как у шара на пружине, как функция частоты ν, или периода T = 1/ν, где T – это время между моментом, когда волна в x₀ находится н а гребне, и моментом, когда она снова приближается к гребню в следующий раз.

Полная формула бесконечной волны

Теперь нам нужна формула для Z(x, t), описывающая волну, изображённую на рис. 3 и 5 (или любую похожую) в точках x в любой момент времени t. Правильный ответ:

Он включает обе формулы, для фиксированной точки во времени и для фиксированной точки в пространстве.

Отметим знак минуса перед x. Я упоминал, что в формулу для Z(x, t₀) можно подставить минус по желанию. С минусом перед x и плюсом перед t формула описывает волну, движущуюся вправо, как на анимациях. Чтобы проверить это, заметьте, что когда t/T – x/λ = 0, волна будет гребнем, потому что cos[0]=1. Когда t = 0, в точке x = 0 гребень. Но если немного сдвинуть t вперёд, допустим, на T/10, то гребень будет в точке x = λ/10, правее от того места, где он был в t = 0 – поэтому гребень (и вся волна) движется вправо.

Рис. 6

Волны, являющиеся функциями x и t, могут двигаться в любом направлении, так что нам просто нужно выбрать правильную формулу для заданной волны. Вообще говоря, когда мы работаем с волнами, которые могут двигаться не только вдоль одного пространственного измерения x, но вдоль всех трёх координат x, y и z, то эти волны могут двигаться в любом направлении, и нам нужно будет выбрать правильную формулу на основании направления движения волны.

Источник

Волны

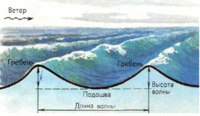
Волна (Wave, surge, sea) — образуется благодаря сцеплению частиц жидкости и воздуха; скользя по гладкой поверхности воды, поначалу воздух создаёт рябь, а уже затем, действует на ее наклонные поверхности, развивает постепенно волнение водной массы. Опыт показал, что водяные частицы не имеют поступательного движения; перемещается только вертикально. Морскими волнами называют движение воды на морской поверхности, возникающее через определённые промежутки времени.

Высшая точка волны называется гребнем или вершиной волны, а низшая точка — подошвой. Высотой волны называется расстояние от гребня до её подошвы, а длина это расстояние между двумя гребнями или подошвами. Время между двумя гребнями или подошвами называется периодом волны.

Содержание

Основные причины возникновения

В среднем высота волны во время шторма в океане достигает 7-8 метров, обычно может растянуться в длину — до 150 метров и до 250метров во время шторма.

Волны, наблюдаемые и в других водных пространствах, могут быть двух родов:

1) Ветровые, созданные ветром, принимающие по прекращении действия ветра установившийся характер и называемые установившимися волнами, или зыбью; Ветровые волны создаются вследствие воздействия ветра (передвижение воздушных масс) на поверхность воды, то есть нагнетания. Причина колебательных движений волн становится легко понятна, если заметить воздействие того же ветра на поверхность пшеничного поля. Хорошо заметна непостоянность ветровых потоков, которые и создают волны.

2) Волны перемещения, или стоячие волны, образуются в результате сильных толчков на дне при землетрясениях или возбужденные, например, резким изменением давления атмосферы. Данные волны носят также название одиночных волн.

В отличие от приливов, отливов и течений волны в не перемещают массы воды. Волны идут, но вода остается на месте. Лодка, которая качается на волнах, не уплывает вместе с волной. Она сможет немного переместиться по наклонной, только благодаря силе земной гравитации. Частицы воды в волне движутся по кольцам. Чем дальше эти кольца от поверхности, тем меньше они становятся и, наконец, исчезают совсем. Находясь в субмарине на глубине 70-80 метров, вы не ощутите действие морских волн даже при самом сильном шторме на поверхности.

Виды морских волн

Волны могут проходить огромные расстояния, не изменяя формы и практически не теряя энергии, долго после того, как вызвавший их ветер утихнет. Разбиваясь о берег, морские волны высвобождают огрмную энергию, накопленную за время странствия. Сила непрерывно разбивающихся волн по-разному изменяет форму берега. Разливающиеся и накатывающиеся волны намывают берег и поэтому называются конструктивными. Волны, обрушивающиеся на берег, постепенно разрушают его и смывают защищающие его пляжи. Поэтому они называются деструктивными.

Низкие, широкие, закругленные волны вдали от берега называются зыбью. Волны заставляют частички воды описывать кружки, кольца. Размер колец уменьшается с глубиной. По мере приближения волны к покатому берегу частицы воды в ней описывают все более сплющенные овалы. Приближаясь к берегу, морские волны больше не могут замкнуть свои овалы, и волна разбивается. На мелководье частицы воды больше не могут замкнуть свои овалы, и волна разбивается. Мысы образованы из более твердой породы и разрушаются медленнее, чем соседние участки берега. Крутые, высокие морские волны подтачивают скалистые утесы у основания, образуя ниши. Утесы порой обрушиваются. Сглаженная волнами терраса — это все, что остается от разрушенных морем скал. Иногда вода поднимается по вертикальным трещинам в скале до вершины и вырывается на поверхность, образуя воронку. Разрушительная сила волн расширяет трещины в скале, образуя пещеры. Когда волны подтачивают скалу с двух сторон, пока не соединятся в проломе, образуются арки. Когда верх арки падает в море, остаются каменные столбы. Их основания подтачиваются, и столбы обрушиваются, образуя валуны. Галька и песок на пляже — это результат эрозии.

Деструктивные волны постепенно размывают берег и уносят песок и гальку с морских пляжей. Обрушивая всю тяжесть своей воды и смытого материала на склоны и обрывы, волны разрушают их поверхность. Они вжимают воду и воздух в каждую трещину, каждую расщелину, часто с энергией взрыва, постепенно разделяя и ослабляя скалы. Отколовшиеся обломки скал используются для дальнейшего разрушения. Даже самые твердые скалы постепенно уничтожаются, и суша на берегу изменяется под действием волн. Волны могут разрушать морской берег с поразительной быстротой. В графстве Линкольншир, в Англии, эрозия (разрушение) надвигается со скоростью 2 м в год. С 1870 г., когда был построен самый большой в США маяк на мысе Гаттерас, море смыло пляжи на 426 м в глубину побережья.

Цунами

Цунами — это волны огромной разрушительной силы. Они вызываются подводными землетрясениями или извержениями вулканов и могут пересекать океаны быстрее, чем реактивный самолет: 1000 км/ч. В глубоких водах они могут быть ниже одного метра, но, приближаясь к берегу, замедляют свой бег и вырастают до 30-50 метров, прежде чем обрушиться, затопляя берег и сметая все на своем пути. 90% всех зарегистрированных цунами отмечено в Тихом океане.

Наиболее распространённые причины.

Около 80% случаев зарождения цунами являются подводные землетрясения. При землетрясении под водой происходит взаимное смещение дна по вертикали: часть дна опускается, а часть приподнимается. На поверхности воды происходят колебательные движения по вертикали, стремясь вернуться к исходному уровню, — среднему уровню моря, — и порождает серию волн. Далеко не каждое подводное землетрясение сопровождается цунами. Цунамигенным (то есть порождающим волну цунами) обычно является землетрясение с неглубоко расположенным очагом. Проблема распознавания цунамигенности землетрясения до сих пор не решена, и службы предупреждения ориентируются на магнитуду землетрясения. Наиболее сильные цунами генерируются в зонах субдукции. Также, необходимо чтобы подводный толчок вошёл в резонанс с волновыми колебаниями.

Оползни. Цунами такого типа возникают чаще, чем это оценивали в ХХ веке (около 7 % всех цунами). Зачастую землетрясение вызывает оползень и он же генерирует волну. 9 июля 1958 года в результате землетрясения на Аляске в бухте Литуйя возник оползень. Масса льда и земных пород обрушилась с высоты 1100 м. Образовалась волна, достигшая на противоположном берегу бухты высоты более 524 м. Подобного рода случаи достаточно редки и, не рассматриваются в качестве эталона. Но намного чаще происходят подводные оползни в дельтах рек, которые не менее опасны. Землетрясение может быть причиной оползня и, например, в Индонезии, где очень велико шельфовое осадконакопление, оползневые цунами особенно опасны, так как случаются регулярно, вызывая локальные волны высотой более 20 метров.

Вулканические извержения составляют примерно 5% всех случаев цунами. Крупные подводные извержения обладают таким же эффектом, что и землетрясения. При сильных вулканических взрывах образуются не только волны от взрыва, но вода также заполняет полости от извергнутого материала или даже кальдеру, в результате чего возникает длинная волна. Классический пример — цунами, образовавшееся после извержения Кракатау в 1883 году. Огромные цунами от вулкана Кракатау наблюдались в гаванях всего мира и уничтожили в общей сложности более 5000 кораблей, погибло около 36 000 человек.

Признаки появления цунами.

Волны-убийцы

Волны-убийцы (Блужда́ющие во́лны, волны-монстры, freak wave — аномальная волна) — гигантские волны, возникающие в океане, высотой более 30 метров, обладают несвойственным для морских волн поведением.

Еще каких-то 10-15 лет назад ученые считали истории моряков об исполинских волнах-убийцах, которые возникают из ниоткуда и топят корабли, всего лишь морским фольклором. Долгое время блуждающие волны считались выдумкой, так как они не укладывались ни в одну существовавшую на то время математические модели расчётов возникновения и их поведения, потому как волны высотой более 21 метра в океанах планеты Земля не могут существовать.

Одно из первых описаний волны-монстра относится к 1826 году. Её высота была более 25 метров и заметили её в Атлантическом океане недалеко от Бискайского залива. Этому сообщению никто не поверил. А в 1840 году мореплаватель Дюмон д’Юрвиль рискнул явиться на заседание Французского географического общества и заявить, что своими глазами видел 35-метровую волну. Присутствующие подняли его на смех. Но историй о громадных волнах-призраках, которые появлялись внезапно посреди океана даже при небольшом шторме, и своей крутизной походили на отвесные стены воды, становилось все больше.

Исторические свидетельства «волн-убийц»

Однако 1 января 1995 года на нефтяной платформе «Дропнер» в Северном море у побережья Норвегии была впервые приборно зафиксирована волна высотой в 25,6 метров, названная волной Дропнера. Проект «Максимальная волна» позволил по-новому посмотреть на причины гибели сухогрузов судов, которые перевозили контейнеры и другие немаловажные грузы. Дальнейшие исследования зафиксировали за три недели по всему земному шару более 10 одиночных гигантских волн, высота которых превышала 20 метров. Новый проект получил название Wave Atlas (Атлас волн), в котором предусматривается составление всемирной карты наблюдавшихся волн-монстров и её последующую обработку и дополнение.

Существует несколько гипотез о причинах возникновения экстремальных волн. Многие из них лишены здравого смысла. Наиболее простые объяснения построены на анализе простой суперпозиции волн разной длины. Оценки, однако, показывают, что вероятность экстремальных волн в такой схеме оказывается слишком мала. Другая заслуживающая внимания гипотеза предполагает возможность фокусировки волновой энергии в некоторых структурах поверхностных течений. Эти структуры, однако, слишком специфичны для того, чтобы механизм фокусировки энергии мог объяснить систематическое возникновение экстремальных волн. Наиболее достоверное объяснение возникновения экстремальных волн должно основываться на внутренних механизмах нелинейных поверхностных волн без привлечения внешних факторов.

Интересно, что такие волны могут быть как гребнями, так и впадинами, что подтверждается очевидцами. Дальнейшее исследование привлекает эффекты нелинейности в ветровых волнах, способные приводить к образованию небольших групп волн (пакетов) или отдельных волн (солитонов), способных проходить большие расстояния без значительного изменения своей структуры. Подобные пакеты также неоднократно наблюдались на практике. Характерными особенностями таких групп волн, подтверждающими данную теорию, является то, что они движутся независимо от прочего волнения и имеют небольшую ширину (менее 1 км), причем высоты резко спадают по краям.

Впрочем, полностью прояснить природу аномальных волн пока не удалось.

Источник