Что может быть больше бесконечности
Какое оно число, что больше бесконечности?
«Две вещи действительно бесконечны: Вселенная и человеческая глупость. Впрочем, насчет Вселенной у меня есть некоторые сомнения». Альберт Эйнштейн
Знак бесконечности имеет разные сферы применения. Многие впервые знакомятся с ним на уроках математики, а еще его используют в физике, логике, философии. Характеризуют его различными неисчисляемыми объектами, у которых нет размера и границ. Современная молодежь символ знака бесконечности использует для украшения своего тела в виде татуировки. Впервые этот знак изобразил математик Джон Валлис в 1655 году. Немного позднее, в 1694 г. швейцарский математик Якоб Бернулли в своей статье опубликовал изображение знака бесконечности, демонстрирующего описанную им плоскую алгебраическую кривую, и назвал его «лемнискатой». С тех пор в мире науки данную фигуру именуют «лемнискатой Бернулли». Так в Древней Греции именовали специальное крепление в виде бантика для венка, победителей в спортивных состязаниях.
По одной из исторических теорий, знак бесконечности был перемещён в современную западную цивилизацию из индийской культурной традиции. По другой версии история зарождения символа бесконечности своими корнями уходит к наскальным изображениям в Тибете. В общем, на сегодняшний день нет точной информации, почему был выбран именно такой символ.
Израильский математик, профессор Дорон Зельбергер, убеждён, что числа не могут увеличиваться бесконечно, и существует такое огромное число, что если прибавить к нему единицу, получится ноль.
Возможно, это число и его значение лежат далеко за пределами человеческого понимания, и вероятно, это число никогда не будет найдено и доказано. Но почему тогда многие так легко оперируют со словом бесконечность, как будто это число?
Некоторые народы до сих пор используют простейшие системы записи чисел. Например, племя Пираха, живущее в Амазонии, применяет очень простую систему нумералов: один, два, много. Пираха не знают чисел больше двух, и у них такие операции, как 2+1 и 2+2, дают одинаковый результат, то есть «много». Они не в состоянии различать числа 3 и 4, не могут выполнять арифметические операции c ними и в целом не в состоянии сказать что-либо об этих числах, поскольку в их языке нет ни слов, ни концепций для этого.
Занимательная Гугология, часть 2. Есть ли что-нибудь за пределами бесконечности?
Дисклеймер: Перед тем как читать эту статью я настоятельно рекомендую ознакомиться с первой частью этого цикла, поскольку многие понятия, которые я использую здесь, там уже были разъяснены, и здесь я повторяться не буду.
Дисклеймер для специалистов и тех кто уже немного в теме: В данной части под бесконечными множествами (∞) подразумеваются только кардинальные (א). В следующей части я объясню, что означают кардинальные множества. Все это сделано для максимального облегчения и так непростого материала.
Бесконечность очень любят математики. Однако физики приходят в ужас, когда в их уравнениях встречается бесконечность. Например, если спросить у физика, что находится внутри черной дыры он, будучи честным, ответит «не знаю», потому что решение уравнения черной дыры выдает в результате ответ, что в ее центре находится бесконечное искривление пространства. Иными словами, как только у физика где-то получается бесконечность он просто разводит руками и уповает на то, что однажды сможет создать уравнение, которое даст более определенный ответ. На самом деле в математике с бесконечностью тоже не все в порядке. До 1908 г. математики пытались доказать существование бесконечности, пока Эрнст Цермело не постановил, что существование бесконечности – это аксиома.
Напомню, что такое аксиомы. Это утверждения, принимаемые без доказательств, на их основе строится вся математика и вообще по-сути любая формализация: письменная, устная или мысленная. Например, в геометрии очевидно, что через две точки можно провести только одну прямую. Только вот это нельзя доказать – это аксиома, так есть и всё, смиритесь с этим!
Даже арифметика, которую проходят в начальной школе имеет свои аксиомы, их четыре. Я записал их здесь в немного измененном, но более понятном виде.
Их нельзя доказать или вывести из других утверждений. Так есть, и бессмысленно спрашивать почему они такие.
Но вернемся к бесконечности. Зачем вообще была нужна эта аксиома, которая вводит ее как должное? Дело в том, что без нее в математике возникало такая неприятная штука, которую называли множество всех множеств. Что ж это за гадость такая? Множество всех множеств – это абстрактное абсолютнейшее множество, которое включает в себя вааааще все, что только возможно, мыслимо и немыслимо. Однако существование такого множества делает математику противоречивой. В историю это противоречие вошло, как парадокс Рассела, в честь математика который его сформулировал.
Парадокс на самом деле весьма прост и звучит так: если существует множество всех множеств, то куда входит это множество. Для наглядности было придумано множество загадок. Мне больше всего нравится эта. Существует страна, в которой есть три закона: все жители должны жить в городах, в каждом городе должен быть мэр, мэр не может жить в одном городе с простыми горожанами. Казалось бы, очевидным решением было создать отдельный город для мэров – но вопрос, где будет жить мэр города мэров?
Если мы вводим бесконечность как аксиому, тогда необходимость в таком множестве автоматически отпадает. А в 1931 г. Курт Гёдель и вовсе доказал, что существование бесконечности может быть только аксиомой, то есть доказать, что бесконечность существует невозможно, можно только принять это.
Итак, бесконечность существует и она больше любого числа.
А если к бесконечности прибавить 1, это что-нибудь изменит? Нам не нужно быть выдающимся математиком, чтобы осознать: сколько не прибавляй к бесконечности, она все равно останется бесконечностью. Хотя выдающиеся математики могут тут с нами поспорить, но об этом я расскажу в третьей части цикла.
То же самое с умножением. Даже если мы сложим или умножим бесконечность саму с собой, ничего не изменится.
Следовательно, вот вам и первые свойства бесконечности:
Дальше ориентироваться в арифметике бесконечностей нам поможет задача, называемая Отель Гильберта. По условиям задачи мы имеем отель с бесконечным количеством номеров, в которых живет бесконечное количество постояльцев. Вопрос, как заселить в отель еще одного человека?
Ответ, звучит так: нужно обратиться к постояльцу из номера «1» с просьбой о переселении в следующий по счету номер, и чтобы он попросил о том же постояльца из того номера, передав, что администрация отеля приносит глубочайшие извинения за неудобства. В итоге все постояльцы все равно останутся с номерами, а у нас появиться одно свободное место.
Наши действия с выселением из четных номеров это все равно, что разделить бесконечность на два. Получается, что бесконечность деленная на любое число тоже дает бесконечность. И правда, ведь мы можем заселять постояльцев через один номер, оставляя их пустыми, так что на каждого постояльца придется по два номера, или через четыре номера, так что на каждого постояльца придется по пять номеров. Можем вообще каждому заселяющемуся отдавать по 10 или 50 номеров, да хоть по ∞ номеров в идеале, все равно в результате такого расточительства гостиничной собственности все постояльцы будут заселены, следовательно:
А раз мы выяснили, что ∞ / ∞ = ∞, это значит что бесконечность всех возможных дробных чисел равна бесконечности всех возможных целых чисел.
Ну а как быть со степенью. По сути, возведение бесконечности в степень – это тоже, что перемножить ее между собой несколько раз. Поэтому, в какую бы степень мы не возвели бесконечность, это не должно ничего изменить в сложившейся ситуации.
Однако возведение в бесконечную степень изменит результат. Но вот так сразу объяснить почему, не получится. Придется зайти издалека.
Для начала вспомним, чем рациональные числа отличаются от иррациональных.
Знаменитая теорема Пифагора, говорит, что если катеты прямоугольного треугольника равны 1, то его гипотенуза будет равна квадратному корню из двух. Понятно, что √2 это нецелое число. Но оно удивительно тем, что не существует дроби, в виде которой можно его представить, поскольку иначе числитель и знаменатель этой дроби должны быть бесконечными.
√2 ≈ 1,41421356237309504880168872420969807856 9671875376948073176679737990732478462107 0388503875343276415727.
По легенде считается, что Пифагор сам пришел к такому выводу. Естественно он понимал, что это будет нецелое число, но поначалу ему и в голову не приходило, что √2 невозможно записать дробью. Он считал, что должна существовать какая-то большая дробь, которая будет равна √2. Пифагор решил выяснить так ли это. Если увеличить стороны катетов до 2, то гипотенуза будет равна √8, что тоже не является целым числом. Пифагор думал, что увеличивая величину катетов, он рано или поздно получит целое число гипотенузы и докажет, что √2 можно записать дробью. Он был полностью обескуражен, когда понял, что в своем эксперименте целого числа он не получит никогда, сколько бы он не увеличивал стороны катетов.
Но какое это отношение имеет к бесконечности? Самое прямое! Когда мы, например, делим бесконечную линию на отрезки, то получаем бесконечность отрезков, которые можно считать. Естественно, если мы попытается их сосчитать, то нам не встретится отрезка под номером √2. Однако если разбить бесконечную линию на безразмерные точки, то где-то на линии можно поставить точку равную отметке в √2. Как это сделать? Очень просто. Берем наш равносторонний прямоугольный треугольник прикладываем его сначала катетом, отмечаем точку 1, затем прикладываем гипотенузой и получаем точку √2. Но проблема в том, что используя традиционное математическое деление получить эту точку невозможно. Значит, сколь малые дробные числа мы бы себе не представили, где-то между ними всегда будут находиться иррациональные числа.
То есть у нас существует две разные бесконечности, одна больше другой. Спрашивать во сколько раз или на сколько раз бессмысленно. Больше и все тут. Их принято записывать с индексами 0 и 1, это называют мощностью бесконечности. То есть теперь ∞ = ∞0
Причем бесконечность бо́льшей мощности с легкостью поглащает бесконечность меньшей мощности: ∞1 + ∞0 = ∞1 и ∞1 ⋅ ∞0 = ∞1
Хорошо, но как со всем этим связано возведение в бесконечную степень? Опять же так сразу понять не получится. Сперва, нам нужно узнать, как хранятся иррациональные числа в компьютере.
Понятно, что иррациональное число это такое число, у которого бесконечная последовательность чисел, после запятой. А компьютер не может хранить бесконечную последовательность. Обычно хранится где-то 14, 15 знаков после запятой, остальные округляются. То есть самое точное значение √2, которое можно использовать в обычной компьютерной программе это 1,4142135623731.
А можно ли повысить точность? В принципе можно, но чтобы понять, как, нужно разобрать как компьютер вообще хранит числа.
Ну, это просто. Итак, сколько видов информации может хранить одна лампочка? Ответ очевиден: 2 – вкл и выкл. А две лампочки? Ответ: 4 – выкл+выкл, вкл+вкл, выкл+вкл, вкл+выкл.
А если у нас n лампочек:
Это выражение основа информатики. Оно называется Булеан. Лампочки это биты, а их булеан (2 n ) это числа, которые могут быть в них закодированы. То есть, имея 1 бит, мы можем закодировать числа от 0 до 1, имея 2 бита от 0 до 3, имея 8 бит от 0 до 255.
Для хранения дробных чисел используется 48 бит, что дает возможность записать любое дробное число с точностью от 0 до 1/281474976710655.
Но в нашем обсуждении не так уж и важно, верна континуум-гипотеза или нет. В любом случае у нас появилась арифметическая возможность получать новые бо́льшие бесконечности.
Но для начала, давайте посмотрим, где можно встретить отражение бесконечностей разных мощностей.
Самое интересное в этом, то что на сегодняшний день неизвестна ни одна совокупность абстрактных объектов, которая составляла бы бесконечности третьей мощности (∞3). То есть, ∞3 не имеет никаких соответствий, даже если попытаться описать с помощью нее всевозможные абстрактные понятия. Ничто известное человечеству не составляет ∞3. Она не имеет никаких аналогий не только в реальности, но и в абстракции.
Можно сказать, что бесконечности выше третьей мощности это всем абстракциям абстракции. Фактически они не имеют никаких практических описательных применений. Тем не менее, приведенная выше формула позволяет нам создавать все более мощные бесконечности:
Хоть при помощи них уже нельзя ничего сосчитать, тем не менее, они существуют. Потому что все это следует из принятых нами аксиом арифметики и аксиомы бесконечности.
Но хорошо, вот мы дошли до бесконечности бесконечной мощности ∞∞, чтобы это не значило. А может ли быть у бесконечной мощности своя мощность, то есть:
А почему бы и нет. Тогда получается за ней последует ∞∞1. Однако некоторые могут скептически отнестись к такой конструкции. И хочу сказать, что ваши сомнения оправданы. Ведь мощности у бесконечностей выражаются натуральными числами, а как мы выяснили, бесконечность натуральных чисел это ∞0, и как такое возможно, что мощности вдруг стали исчиляться ∞1? Отвечаю: это возможно, но я пока не буду объяснять почему, скажу лишь, что такую конструкцию допускает континуум-гипотеза, подробнее об этом я расскажу в третьей части цикла.
С ней вроде бы все понятно, с ее помощью можно увеличивать вложенность бесконечных мощностей. На очереди пентация бесконечностей.
Многим может показаться, что всё, финиш, дальше продвигаться некуда. Но давайте представим, что в этой лестнице не просто ∞0 ступенек, а ∞1 ступенек. Некоторые из вас опять же возразят: как такое может быть, ведь ступеньки в этой лестнице отдельные счетные элементы и все их бесконечное множество не может превыщать по мощности ∞0. И опять же отвечу, что континуум-гипотеза это допускает, как допускает существование ∞∞1, как и обещал продробнее это будет рассмотрено в третьей части цикла. Пока поверьте на слово, что это возможно.
Теперь используя этот нюанс, попробуем выразить хескацию бесконечностей. Чтобы понять как, смотрите на рисунок ниже.
Вот этот последний монстр и будет ∞[6]∞. То есть у нас уже не просто лестница бесконечностей. А это лестница длиною в лестницу бесконечностей, которая длиною в лестницу бесконечностей, которая длиною в лестницу бесконечностей, которая. (и.т.д).
Визуализировать ∞[7]∞ будет еще сложнее. Это будет выглядеть так:
Конечно вам может показаться, что все это пустые измышления. Может быть и так, но раз математика позволяет нам создавать такие структуры это значит, что они существуют, пусть не в реальности, пусть как абстракции, но существуют.
А может гипероператор быть больше чем обычная бесконечность, например ∞[∞1]∞? Может. И это все равно, что ∞[∞[3]∞]∞. А может быть еще больше? Конечно. Может быть и таким ∞[∞∞]∞ = ∞[∞[4]∞]∞. Пусть хоть он будет лесницей бесконечности ∞[∞∞∞∞. ]∞ = ∞[∞[5]∞]∞. Пожалуйста. Вот только мы же не сможем визуализировать мощности таких структур, но опять же, это не значит, что они не существуют.
Итак, раз у нас уже начались вложения гипероператора, давайте сразу перейдем к ∞[∞[∞]∞]∞, затем к ∞[∞[∞[∞]∞]∞]∞ и так далее.
Затем мы можем привлечь функцию superhyper(), а после чего функцию quasi(), которые как вы помните я ввел еще в первой части цикла. Или можем сразу перейти к более сильным нотациям, с которыми я вас так же вкратце познакомил в конце первой части.
Врятли кто возьмется объяснить простым языком, что все это значит. Однако это кажется просто невероятным, как возможности нашего разума, как сила математического формализма способна создавать такие сущности, которые больше не только любых физических величин, но и любых мыслимых абстрактных объектов.
Пока что ничего бо́льшего чем разрядовая недостижимость не придумали.
Но вопрос все равно остался открытым, доколе можно вводить новые аксиомы, которые будут позволять нам увеличивать невообразимость создаваемых нами сущностей?
Что ж, математики не знают ответа на этот вопрос. На самом деле ответа тут может быть два:
1 – однажды мы дойдем до того, что любая новая аксиома сделает противоречивыми все наши построения и значит всё, бо́льших абстракций придумать невозможно.
2 – новым аксиомам может не быть конца.
На этом предлагаю остановиться и сделать передышку. В третей части я расскажу как можно упорядочить бесконечность, и как ни странно, понимание этого еще на один шаг приблизит нас к построению самого большого из придуманных чисел, о чем я поведаю уже в четвертой части цикла.
Какое оно, число, что больше бесконечности?
Понедельник! Пора сломать мозг!
«Две вещи действительно бесконечны: Вселенная и человеческая глупость. Впрочем, насчет Вселенной у меня есть некоторые сомнения». Альберт Эйнштейн
Знак бесконечности имеет разные сферы применения. Многие впервые знакомятся с ним на уроках математики, а еще его используют в физике, логике, философии. Характеризуют его различными неисчисляемыми объектами, у которых нет размера и границ. Современная молодежь символ знака бесконечности использует для украшения своего тела в виде татуировки. Впервые этот знак изобразил математик Джон Валлис в 1655 году. Немного позднее, в 1694 г. швейцарский математик Якоб Бернулли в своей статье опубликовал изображение знака бесконечности, демонстрирующего описанную им плоскую алгебраическую кривую, и назвал его «лемнискатой». С тех пор в мире науки данную фигуру именуют «лемнискатой Бернулли». Так в Древней Греции именовали специальное крепление в виде бантика для венка, победителей в спортивных состязаниях.
По одной из исторических теорий, знак бесконечности был перемещён в современную западную цивилизацию из индийской культурной традиции. По другой версии история зарождения символа бесконечности своими корнями уходит к наскальным изображениям в Тибете. В общем, на сегодняшний день нет точной информации, почему был выбран именно такой символ.
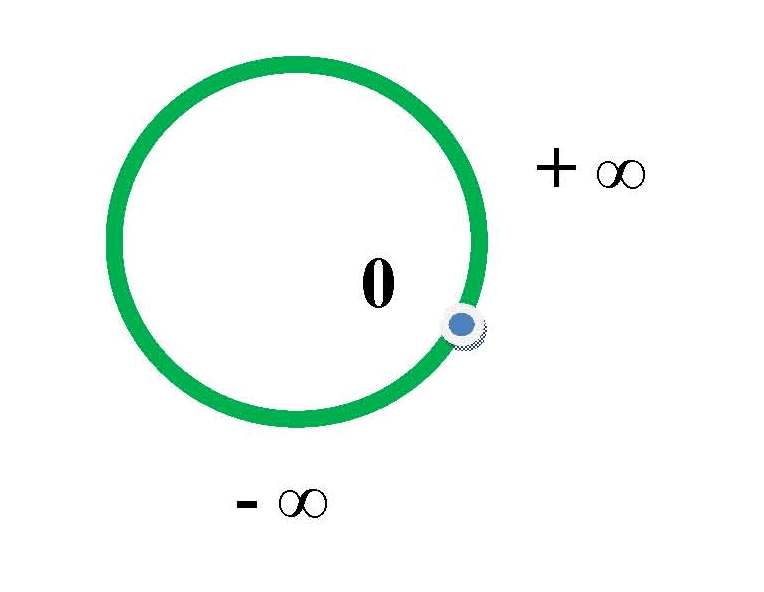
Израильский математик, профессор Дорон Зельбергер, убеждён, что числа не могут увеличиваться бесконечно, и существует такое огромное число, что если прибавить к нему единицу, получится ноль.
Насчёт единицы не уверен. В тему сильно не углублялся, но сдаётся мне, что на множестве натуральных чисел такое может не проканать (не знаю).
А вот с рациональными.
Ну а здесь можно для наглядности почитать про Риманову геометрию, чтобы представить себе такое. Если влом, то посмотрите на глобус, там есть геодезические кривые и полюса (плоскоземельщикам не читать).
И картинку посмотреть:
Возможно, это число и его значение лежат далеко за пределами человеческого понимания, и вероятно, это число никогда не будет найдено и доказано. Но почему тогда многие так легко оперируют со словом бесконечность, как будто это число?
Некоторые народы до сих пор используют простейшие системы записи чисел. Например, племя Пираха, живущее в Амазонии, применяет очень простую систему нумералов: один, два, много. Пираха не знают чисел больше двух, и у них такие операции, как 2 1 и 2 2, дают одинаковый результат, то есть «много». Они не в состоянии различать числа 3 и 4, не могут выполнять арифметические операции c ними и в целом не в состоянии сказать что-либо об этих числах, поскольку в их языке нет ни слов, ни концепций для этого.
1. Актуальная бесконечность существовать не может.
2. Безначальный ряд временных событий представляет собой актуальную бесконечность.
3. Следовательно, безначальный ряд временных событий не может существовать.
Рассмотрим вначале первую посылку: Актуальная бесконечность не может существовать.
Что я имею в виду под актуальной бесконечностью? Множество объектов считается актуально бесконечным, если часть этого множества равна его целому. Так например, какой рад длиннее:
По общепринятым математическим представлениям, эти ряды эквивалентны, потому что они оба актуально бесконечны. Это кажется странным: ведь в правом ряду есть два числа, отсутствующие в левом. Но это лишь показывает, что в актуально бесконечном множестве часть (левый ряд) равна целому (правый ряд).
По той же причине математики утверждают, что ряд чётных чисел равен ряду натуральных чисел — несмотря на то, что ряд всех натуральных чисел содержит все чётные плюс бесконечное число нечётных чисел.
При этом не надо смешивать понятия актуальной бесконечности — и потенциальной бесконечности.
По мнению великого немецкого математика Давида Гилберта, главное различие между актуальной и потенциальной бесконечностью заключается вот в чём. Потенциально бесконечное есть всегда нечто возрастающее и имеющее пределом бесконечность, тогда как актуальная бесконечность — это завершённое целое, в действительности содержащее бесконечное число предметов.
Интересным примером этих двух типов бесконечности могут послужить два ряда событий: произошедших до и после какой-либо точки в прошлом.
Возьмём, например, момент в 1845 г., когда родился Георг Кантор, отец теории множеств.
В обоих случаях мы имеем в виду события, действительно случившиеся.
Точка, называемая «настоящее время», разумеется, не стоит на месте, а скользит вперёд. (По сути дела, это граница между событиями уже реализованными и ещё не реализованными.) Поэтому количество событий «после» (т. е. между 1845 г. и настоящим временем), хотя и в каждый конкретный момент конечное, постоянно возрастает. Оно никогда не реализовано до конца, и потому потенциально бесконечно.
Но ряд событий «до» полностью реализован, завершён и не возрастает. И если атеисты правы, и у Вселенной не было начала, то такой ряд бесконечен. Бесконечен актуально, реально.
В ходе наших рассуждений очень важно эти два понятия (актуальной и потенциальной бесконечности) не путать.
Второе пояснение касается слова «существовать». Когда я говорю, что актуальная бесконечность не может существовать, я имею в виду — существовать в реальном мире, или существовать не только в уме. Я вовсе не отрицаю законность использования понятия актуальной бесконечности в математике (оперирующей лишь мысленной реальностью). Я лишь утверждаю, что актуальная бесконечность не может существовать в физическом мире звёзд, планет, камней и людей.
Несколько примеров покажут абсурдность такого допущения.
Допустим, что существует библиотека, содержащая реально бесконечное число книг. Представим себе, что книги в ней только двух цветов, чёрного и красного, и что они стоят на полках, чередуясь: чёрная, красная, чёрная, красная, и т.д. Если кто-то скажет нам, что число чёрных книг равно числу красных, мы, вероятно, не удивимся. Но поверим ли мы, если нам скажут, что число чёрных книг равно числу чёрных и красных книг вместе? Ведь в таком собрании мы обнаружим все чёрные книги плюс бесконечное число красных книг!
Или же представим себе, что у нас есть книги трёх цветов, четырёх, пяти или даже ста. Поверим ли мы, что книг одного цвета столько же, сколько всего книг в библиотеке?
Несколько примеров покажут абсурдность такого допущения.
Допустим, что существует библиотека, содержащая реально бесконечное число книг. Представим себе, что книги в ней только двух цветов, чёрного и красного, и что они стоят на полках, чередуясь: чёрная, красная, чёрная, красная, и т.д. Если кто-то скажет нам, что число чёрных книг равно числу красных, мы, вероятно, не удивимся. Но поверим ли мы, если нам скажут, что число чёрных книг равно числу чёрных и красных книг вместе? Ведь в таком собрании мы обнаружим все чёрные книги плюс бесконечное число красных книг!
Или же представим себе, что у нас есть книги трёх цветов, четырёх, пяти или даже ста. Поверим ли мы, что книг одного цвета столько же, сколько всего книг в библиотеке?
Продолжим наши рассуждения. Предположим, что у каждой книги на корешке отпечатан номер. Поскольку библиотека реально бесконечна, каждое возможное число отпечатано на какой-либо из книг. Поэтому мы не можем добавить к библиотеке ещё одну книгу, ибо какой номер ей дать? Всё номера уже заняты. Таким образом, новой книге нельзя дать номера! Но это абсурд, так как в действительности предметы всегда можно нумеровать.
Если бы бесконечная библиотека существовала, то к ней невозможно было бы добавить ещё одну книгу. (Не потому ли, что она уже включала бы все существующие книги, и новую просто неоткуда было бы взять? Нет, ведь достаточно вырвать по листку из каждой книги первой сотни, склеить их вместе, поставить эту новую книгу на полку, и всё — библиотека пополнена!) Поэтому напрашивается единственно возможный вывод: библиотека, актуально бесконечная, — существовать не может.
Но предположим, что мы можем пополнить эту библиотеку, и я ставлю книгу на полку. По утверждению математиков, число книг в библиотеке осталось прежним. Как это может быть? Ведь мои опыт говорит: если я поставил книгу на полку, то там стало книгой больше, а если снял, то одной меньше.
Мне легко вообразить себя, ставящего и снимающего эту книгу. Должен ли я впрямь всерьёз поверить, что когда я добавляю книги, их число не увеличивается, а когда убираю — не уменьшается? А если я добавлю к этой библиотеке бесконечное число или даже бесконечность бесконечностей книг? Неужели и теперь в библиотеке ни на одну книгу не больше, чем прежде? Мне в это трудно поверить. А вам?
А теперь давайте, наоборот, выдавать книги из библиотеки. Предположим, в понедельник мы выдали книгу номер восемь. Разве число книг не уменьшилось на одну?
Во вторник — выдадим все книги с нечётными номерами. Ушло бесконечное число книг, но математики скажут, что в библиотеке книг меньше не стало.
Допустим, что в среду мы выдали книги за номерами 4, 5, 6. и до бесконечности. Единым махом библиотека практически вся опустела, бесконечное число книг сведено к конечному: к трём. Но позвольте, ведь мы на этот раз выдали столько же книг, что и во вторник! Почему же такая разница? И кто поверит, что такая библиотека может на самом деле существовать?
Все эти примеры иллюстрируют тот факт, что актуальная бесконечность не может иметь места в физическом мире. Я вновь хочу подчеркнуть: это ничем не грозит теоретической системе, введённой в современную математику Г. Кантором. Больше того: даже такие энтузиасты математических теорий бесконечного, как Д. Гилберт, охотно соглашаются с тем, что понятие актуальной бесконечности — это только идея, не имеющая никакого отношения к реальному миру.Поэтому — мы вправе заключить: актуальная бесконечность существовать не может.
Вторая посылка: Ряд событий во времени, не имеющий начала, представляет собой актуальную бесконечность.
Под «событием» я подразумеваю любую перемену, происходящую в физическом мире. То есть: если ряд прошлых событий (или перемен) всё время уходит в прошлое и никогда не имеет начала, то в этом случае, взятые все вместе, эти события составляют актуально бесконечное множество.
Допустим, мы спрашиваем, откуда появилась такая-то звезда. Нам отвечают, что она появилась в результате взрыва звезды, существовавшей до этого. Тогда мы спрашиваем, откуда появилась та звезда? Она тоже возникла из звезды, существовавшей до неё. А эта звезда откуда? Из другой, предыдущей звезды — и так далее. Этот ряд звёзд будет примером безначального во времени ряда событий.
Тогда, если Вселенная существовала всегда, ряд всех событий прошлого в их совокупности составит актуальную бесконечность: потому что каждому событию в прошлом предшествовало другое событие. Таким образом, ряд прошлых событий будет бесконечным.
Но не будет ли он потенциально бесконечным? Нет, ибо мы видели, что прошлое завершено и актуально, — лишь будущее может быть охарактеризовано как потенциально бесконечное. Поэтому представляется очевидным, что безначальный ряд событий во времени является актуальной бесконечностью.
Это приводит нас к нужному заключению. безначальный ряд событий во времени существовать не может. (Мы установили ранее, что актуально бесконечное не может существовать в действительности. И если безначальный ряд временных событий есть актуальная бесконечность, то такой ряд не может существовать.)
Значит, ряд всех событий прошлого обязан иметь начало. Но ведь история Вселенной и есть ряд всех свершившихся событий! Поэтому у Вселенной должно быть начало.
Несколько примеров пояснят этот аргумент.
Мы знаем, что если бы актуальная бесконечность могла существовать в действительности, к ней невозможно было бы ничего прибавить. Но к ряду событий во времени происходят добавления каждый день — или, по крайней мере, нам так кажется. Если же этот ряд актуально бесконечен, то число событий, случившихся до настоящего момента, — не больше, чем, скажем, число событий до 1789 года или до любой другой точки в прошлом, сколь угодно далёкой.
Ещё пример. Вообразим, что вокруг Солнца уже целую вечность вращаются две планеты. Допустим, что одна проходит свою орбиту за три года, другая — за год. Таким образом, на каждый оборот одной приходятся три оборота другой. Вопрос: если они движутся вечно, которая из этих планет сделала больше орбитных оборотов? Ответ: обе сделали одинаковое число оборотов. Но это явный абсурд, ведь здравый смысл подсказывает: чем дольше они вращаются, тем сильнее увеличивается разрыв. Как же может число оборотов быть равным?
Эти примеры подчёркивают абсурдность идеи безначального ряда событий во времени. Поскольку такой ряд является актуально бесконечным, а актуальная бесконечность существовать не может, то и этот ряд невозможен. Это значит, что Вселенная когда-то начала своё существование, что и требовалось доказать.