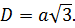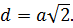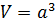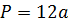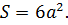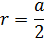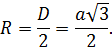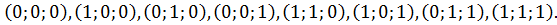Букв куб что это

Буква в кубе

Описание презентации по отдельным слайдам:

Описание слайда:

МОУ «Средняя школа №17 г.Калуги»
10 «Б» класс
Пидриксон
Владислав Александрович
представляет.

Описание слайда:

Описание слайда:

Описание слайда:

Действительно возможность создавать что-либо новое, необычное закладывается в детстве через развитие высших психических функций, таких как мышление и воображение.
Воображение – это присущая только человеку возможность создания новых образов путём переработки предшествующего опыта. Воображение часто называют фантазией. Воображение отражает действительность, однако с его помощью осуществляется мысленный отход за пределы непосредственно воспринимаемого.
Любое обучение связано с необходимостью что-то представлять, воображать, оперировать абстрактными образами и понятиями. Всё это невозможно сделать без воображения и фантазии.
Отечественный психолог В. Н. Брушлинский считал, что воображение – одна из форм мышления. Развитие воображения проходит две фазы и очень тесно связано с развитием рассудочной деятельности. Эту связь отражает так называемая «кривая Рибо».

Описание слайда:

I R H
Первый период развития воображения иллюстрирует кривая I-M, а рассудочную деятельность R-X. Этот период охватывает приблизительно первые 15 лет жизни человека. Затем рассудочна деятельность сохраняет своё прогрессивное развитие (кривая Х-О), а воображение, в большинстве случаев, характеризуется падением интенсивности (кривая М-Н).Чем меньше падение кривой М-Н, тем больше способности проявляет человек. Когда же кривая воображения сохраняет стабильность или своё прогрессивное направление (M-N), то можно говорить об одарённости или гениальности.

Описание слайда:

Воображение и фантазия присущи каждому человеку, но люди различаются по направленности этой фантазии, её силе и яркости.
Затухание функции воображения с возрастом – отрицательный момент для личности. Вместе с тем, воображение может не только облегчить процесс обучения, но и само развиться при соответствующей организации учебной деятельности.
Мышление – это высшая форма творческой активности человека.
Уже давно учёные пытались разгадать загадку творчества. Первыми объектами изучения были люди науки и искусства. Анализировались их дневники, письма, высказывания. Большинство авторов великих изобретений выделяли две стадии творческого процесса: первая стадия – длительное размышление над изученными фактами и явлениями; вторая стадия – короткое озарение и интуитивно принятые решения. Изобретатель Томас Эдисон так определил процесс творчества: «Изобретение – это 99% пота и 1% вдохновения».

Описание слайда:

Воображение получает развитие при решении различных ребусов, шарад, кроссвордов и других занимательных задач.
Наблюдая за одноклассниками на уроках черчения, я заметил, что не все хорошо справляются с проекционными задачами. Я решил составить свои собственные задачи, которые были бы интересны и занимательны.
Цель моей работы – соединить пространственные задачи с другими занимательными задачами и разработать их.

Описание слайда:

В моей работе Вам
предлагаются
проекционные кубы.
Пример такого куба
приведён в левом верхнем
углу. В каждом кубе с помощью линий зашифрована одна, две или три буквы.
На основе этого можно разделить задачи на три уровня сложности.

Описание слайда:

Чтобы узнать какие
буквы зашифрованы
в кубе нужно
мысленно
посмотреть на
куб сверху, справа, или
спереди. Тогда с помощью
воображения можно понять, как
спроецируются линии и какую букву
можно увидеть.

Описание слайда:

Рассмотрим конкретный пример.
В большом кубе зашифровано три
первые буквы латинского алфавита
А, В, С. Если
представить
вид куба справа,
то мы увидим
букву А, если
представить вид куба спереди, то
мы увидим букву В, если же представить
вид сверху, то мы увидим букву С.

Описание слайда:

Описание слайда:

Теперь перейдём непосредственно к задачам.

Описание слайда:

Задачи первого уровня сложности.
В первом уровне сложности в каждом кубе зашифрована только одна буква. Её можно увидеть только с одной стороны, если смотреть с других сторон, то будут видны хаотично расположенные линии. Буквы зашифрованы таким образом, что после разгадывания получится набор букв, расположенных в алфавитном порядке. Из этих букв нужно составить слово. В качестве подсказки даётся краткое пояснение к слову.
1) «Измеряющий вокруг».

Е Е И М П Р Р Т
Ответ: периметр.

Описание слайда:

2) «Идущая от угла к углу».

А А Г Д И Л Н О Ь
Ответ: диагональ.

3) 10 тысяч в древнерусском счёте.

Описание слайда:

Задачи второго уровня сложности
Во втором уровне сложности в каждом кубе зашифровано две буквы. Их можно увидеть с двух сторон, если смотреть с третьей стороны, то будут видны хаотично расположенные линии. Во втором уровне в кубах я зашифровал имена. В качестве подсказки даётся их перевод.
1)Пальма (древнееврейское).

Н А М Н О А
Ответ: Тамара.

Описание слайда:

2) Мир (древнегреческое).

С Р И И Я
Ответ: Ирина.
3) Могучий медведь (кельтское).

Н Р Т О С
Ответ: Артур.

Описание слайда:

Задачи третьего уровня сложности.
В третьем уровне сложности в каждом кубе зашифровано три буквы. С какой бы стороны вы не смотрели, всё равно будет видна буква. После разгадывания, из множества полученных букв, нужно составить слово. В качестве подсказки даётся краткое пояснение к слову.
Многие студенты с этим английским промышленником встречаются очень часто.

О П Э С Н Г
Ответ: ватман.

Описание слайда:

2) За этой геометрической фигурой ели древние греки.

Е С О П Е Г С Н
Ответ: трапеция.

Описание слайда:

В процессе создания моей работы я предложил одноклассникам попробовать решить некоторые задачи, а кое-кто и сам попросил. Не все сразу справились с заданиями, но главное, что всем понравилось разгадывать слова таким интересным способом.
Мне кажется, что мои задачи могут быть полезны на уроках черчения (первый уровень сложности), как задачи на олимпиадах (второй и третий уровни), и просто, как задачи для увлекательного проведения досуга.
Эта работа нравится мне тем, что оставляет простор для творчества, так как в кубы можно вписывать разные слова и потом преобразовывать полученное в задачи со словами. При этом узнаёшь немало интересных сведений об истории слов и их значении.

Описание слайда:

Список использованной литературы:
1) Л. Ю, Субботина «Развитие воображения у детей», «Академия развития», Ярославль, 1996.
2) А. Е. Симановский «Развитие творческого мышления у детей», «Академия развития», Ярославль, 1996.
3) «Тайна имени», «Владис», Ростов-на-Дону, 2001.

Описание слайда:

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Источник

Среди многогранников куб – это один из наиболее известных объектов, знакомых с далёкого детства. Более подробно эта тема изучается на уроках геометрии в старших классах, когда от фигур на плоскости переходят к телам в пространстве.

Кубу можно дать определение различными способами, каждый из которых только подчеркнёт тот или иной класс тел в пространстве, выделит основные признаки и особенности:

многогранник, у которого все рёбра равны, а грани попарно перпендикулярны;

прямая призма, все грани которой есть квадраты;

прямоугольный параллелепипед, все рёбра которого равны.

Всеми этими и многими другими подобными формулировками геометрия позволяет описывать одну и ту же фигуру в пространстве.

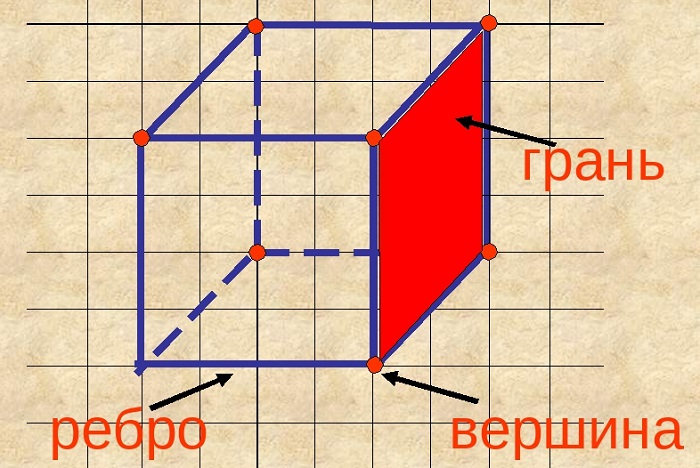
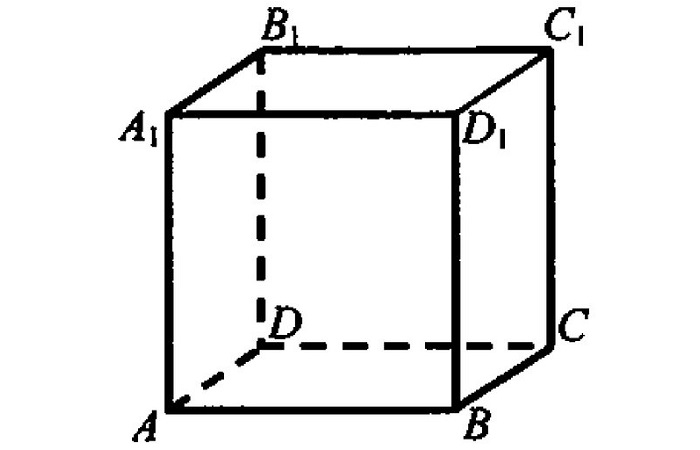
Элементы куба

Основными элементами многогранника считаются грани, рёбра, вершины.

Грань

Плоскости, образующие поверхность куба, называются гранями. Другое название – стороны.

Интересно, сколько граней у куба и каковы их особенности. Всего граней шесть. Две из них, параллельные друг другу, считаются основаниями, остальные – боковыми.

Грани куба попарно перпендикулярны, являются квадратами, равны между собой.

Ребро

Линии пересечения сторон называются рёбрами.

Не каждый школьник может ответить, сколько рёбер у куба. Их двенадцать. Они имеют одинаковые длины. Те из них, что обладают общим концом, расположены под прямым углом по отношению к любому из двух остальных.

Рёбра могут пересекаться в вершине, быть параллельными. Не лежащие в одной грани ребра, являются скрещивающимися.

Вершина

Точки пересечения рёбер называются вершинами. Их число равно восьми.

Центр грани

Отрезок, соединяющий две вершины, не являющийся ребром, называется диагональю.

Пересечение диагоналей грани считается центром грани – точкой, равноудалённой от всех вершин и сторон квадрата. Это есть центр симметрии грани.

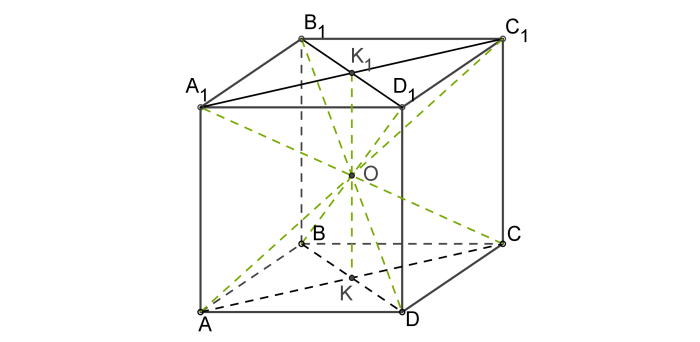
Центр куба

Пересечение диагоналей куба является его центром – точкой, равноудалённой от всех вершин, рёбер и сторон многогранника.

Это есть центр симметрии куба.

Ось куба

Рассматриваемый многогранник имеет несколько осей ортогональной (под прямым углом) симметрии. К ним относятся: диагонали куба и прямые, проходящие через его центр параллельно рёбрам.

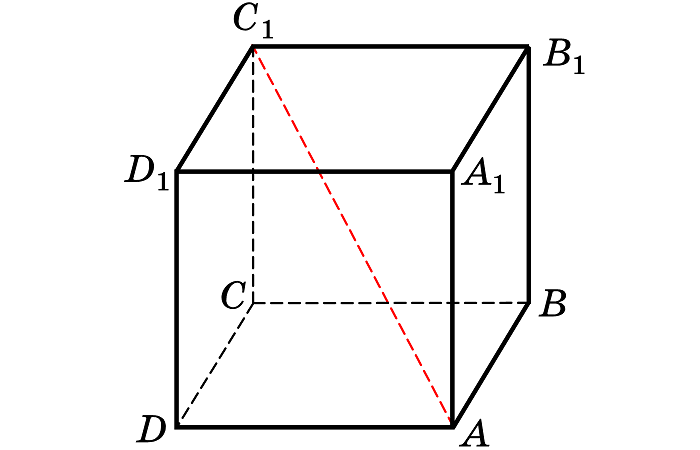
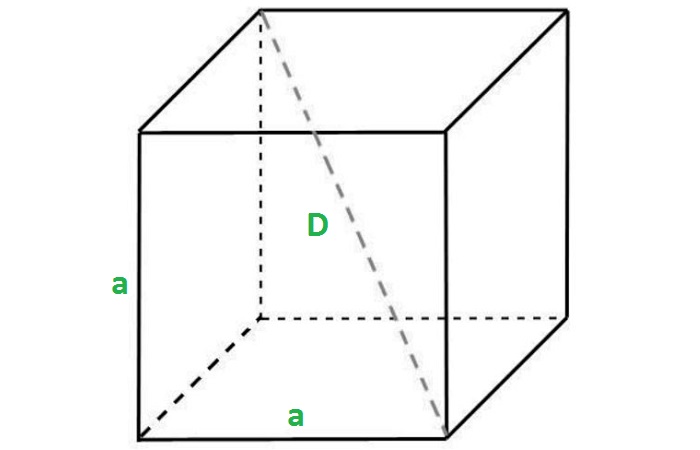
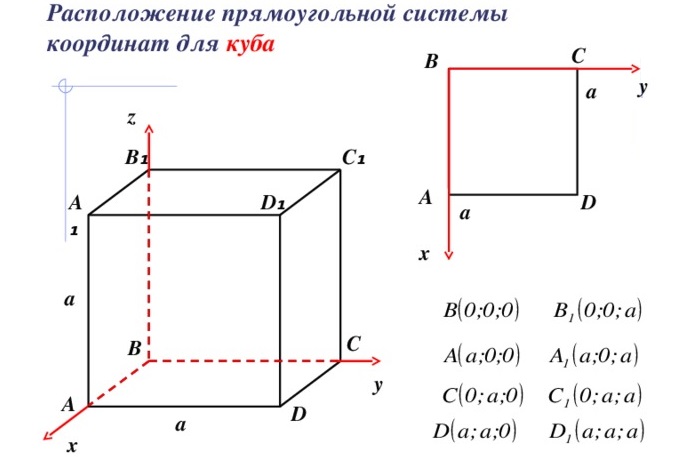
Диагональ куба

Отрезок, соединяющий две вершины, не принадлежащие одной стороне, называется диагональю рассматриваемого многогранника.

Учитывая, что ребра куба имеют равные измерения a, можно найти длину диагонали:

Формула доказывается с помощью дважды применённой теоремы Пифагора.

Все диагонали куба равны между собой и точкой пересечения делятся пополам.

Диагональ грани куба

Длина диагонали грани в √2 раз больше ребра, то есть:

Эта формула доказывается также с помощью теоремы Пифагора.

Объем куба

Как для любого параллелепипеда, объём куба равен произведению всех трёх измерений, которые в данном случае равны:

Периметр куба

Сумма длин всех рёбер равна:

Площадь поверхности

Сумма площадей всех граней называется площадью поверхности куба. Она равна:

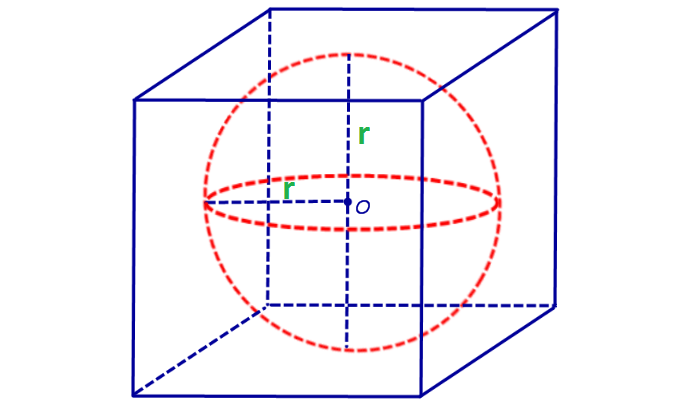
Сфера, вписанная в куб

Такая сфера имеет центр, совпадающий с центром куба.

Радиус равен половине ребра:

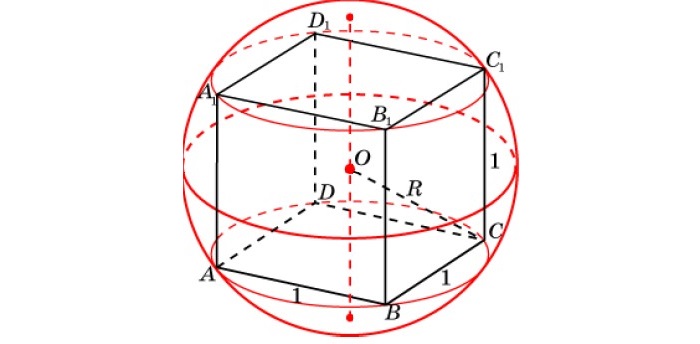
Сфера, описанная вокруг куба

Как для вписанной сферы, центр совпадает с точкой пересечения диагоналей, радиус равен половине диагонали:

Координаты вершин куба

В зависимости от расположения фигуры в системе координат, можно по-разному рассчитывать координаты вершин.

Наиболее часто используют следующий способ. Одна из вершин совпадает с началом координат, рёбра параллельны осям координат или совпадают с ними, координаты единичного куба в этом случае будут равны:

Такое расположение удобно для введения четырёхмерного пространства (вершины задаются всеми возможными бинарными наборами длины 4).

Свойства куба

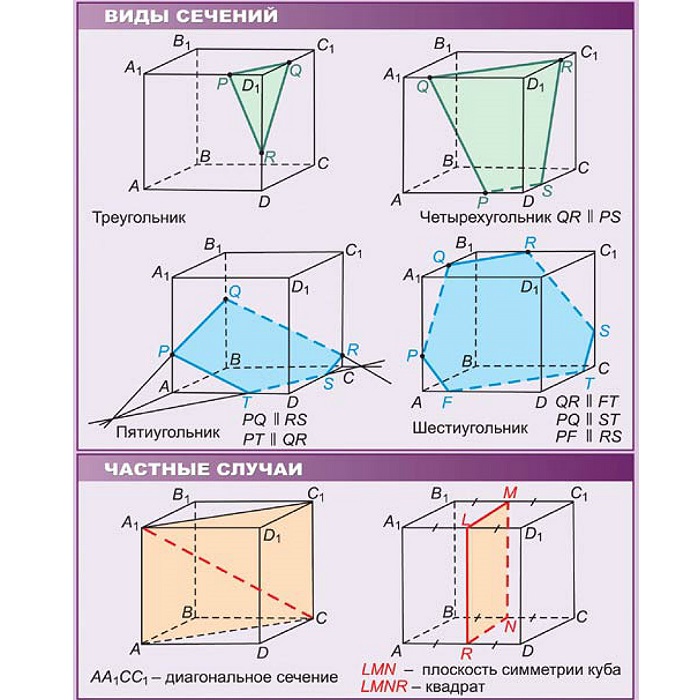
Плоскость, рассекающая куб на две части, есть сечение. Его форма выглядит как выпуклый многоугольник.

Построение сечений необходимо для решения многих задач. Как правило, используется метод следов или условие параллельности прямых и плоскостей.

у куба все грани равны, являются квадратами;

у куба все рёбра равны;

один центр и несколько осей симметрии.

Источник

Булевы функции и булев куб

В дискретной математике большую роль играют конечные функции. Конечной функцией называют отображение одного конечного множества в другое. Важный класс таких функций образуют булевы функции.

Булева функция (от переменных) — это произвольное отображение вида

т.е. булева функция определена на множестве всех n-элементных (при ) последовательностей (или n-компонентных кортежей) нулей и единиц и принимает два возможных значения: 0 и 1.

С понятием булевой функции тесно связаны понятия булевой константы и булева переменного. (В литературе по теории булевых функций традиционно употребляется термин «булева переменная» (в женском роде).)

Пример 6.1. В булевом кубе имеем причем второй из этих наборов доминирует над первым, а третий — над вторым (но, естественно, третий уже не доминирует над первым, а лишь строго больше его). Наборы же и — несравнимые элементы, так как первая компонента второго набора больше первой компоненты первого набора, но зато вторая компонента первого набора больше второй компоненты второго набора. Подчеркнем также, что описанное сравнение наборов возможно только для фиксированной размерности и никак нельзя сравнивать наборы разных размерностей.

Булевый порядок

Рассмотренное отношение порядка на будем называть булевым порядком.

Булев куб как упорядоченное множество, можно изобразить в виде диаграммы Хассе. На рис. 6.1 приведены диаграммы Хассе для булевых кубов размерностей от 0 до 4.

Каждый уровень представляющей булев куб сети состоит из всех вершин, соответствующих наборам, у которых ровно компонент отличны от нуля (множество всех таких наборов для фиксированного называют k-слоем булева куба ).

На рис. 6.2 приведено изображение булева куба в виде сети.

Каждая из сумм в неравенстве (6.2) есть не что иное, как представление некоторого натурального числа (включая и нуль) в двоичной системе счисления (при числе разрядов, равных фиксированной размерности ). На каждый булев вектор можно смотреть как на такое представление (двоичный код) натурального числа, и лексикографический порядок на булевом кубе есть не что иное, как естественный числовой порядок на подмножестве множества (при условии, что числа заданы в двоичной системе счисления). Более строго: упорядоченное множество изоморфно подмножеству с естественным числовым порядком.

Заметим, что отношение лексикографического порядка является, в отличие от булева порядка, отношением линейного порядка.

Однако лексикографический порядок при изучении булевых кубов играет вспомогательную роль. В частности, при изображении булевых кубов (в виде диаграмм Хассе или в виде сети) принято располагать вершины каждого k-слоя в лексикографическом порядке (по возрастанию — слева направо или сверху вниз). Везде в дальнейшем, рассуждая о булевом кубе как об упорядоченном множестве, мы имеем в виду булев порядок.

Грань булева куба

Источник

Таблица кубов и квадратов, как состовлять и найти

Как появилось понятие куб числа?

Древнегреческие математики оперировали так называемыми фигурными числами – числами, которые можно представить в виде фигуры. Выделялись, например:

Последовательность кубов натуральных чисел выглядит так

Полезно будет запомнить, хотя бы те, что меньше тысячи. Особенно мне нравится число 729. Посмотрите:

Еще несколько интересных свойств кубов чисел:

Вот так, к слову выглядит формула вычисления суммы первых кубов чисел:

Степень с натуральным показателем

Проще всего определяется степень с натуральным (то есть целым положительным) показателем.

Выражения «возвести в квадрат» и «возвести в куб» нам давно знакомы.
Возвести число в квадрат — значит умножить его само на себя.

Возвести число в куб — значит умножить его само на себя три раза.

Возвести число в натуральную степень — значит умножить его само на себя раз:

Теория

Куб числа – это результат умножения числа само на себя три раза. Операция вычисления куба числа – это частный случай возведения числа в степень, в данном случае в втретью:

Данное выражение читается: «возвести в куб число 6» или «6 в кубе».

Возвести в куб онлайн

Как возвести число в куб онлайн!? Введите нужное число, которое требуется возвести в куб и нажмите возвести в куб. Справа от равно появится число, которое возвели в куб
Ну и далее пробежимся по нескольким поисковым запросам, которые так или иначе вы задаете в строке поиска!

Дополнительная информация

Квадратом числа называют произведение двух одинаковых множителей.

Мы уже пробовали находить квадраты первого десятка натуральных чисел.

Возводить двузначные числа, трехзначные и т.д. числа немного сложнее, главное хорошо знать и помнить таблицу умножения чисел.

Существует способ быстрого возведения в квадрат двухзначных чисел, которые оканчиваются на цифру 5.

1) Первую цифру числа, возводимого в квадрат, необходимо умножить на сумму этого числа и единицы.

2) Записать полученное число- это будут первые цифры ответа (с этих цифр начинается ответ).

3) Ответ всегда будет заканчиваться на 25 (т.е. в конце ответа всегда будет стоять число 25).

4) Приписываем к числу, полученному в п 2, число 25, получаем ответ.

Рассмотрим поясняющий пример.

Найдем квадрат 65.

65 2 = 65 ∙ 65

6 ∙ (6 + 1) = 6 ∙ 7 = 42

Запишем число 42 и припишем к нему число 25.

65 2 = 4225

Проверим: Так как квадрат числа- это произведение двух одинаковых множителей 65 2 = 65 ∙ 65, то

65 2 = 65 ∙ 65 = 4225

Получили все тот же ответ: 65 2 = 4225

Источник

Задачи с кубиками, содержащие буквы

Истинный педагог постарается сделать учение занимательным, но никогда не лишит его характера серьезного труда, требующего усилия воли.

Данная статья является продолжением цикла статей, посвященных различным заданиям с кубиками и изданный ранее (https://urok.1sept.ru).

Напомним, что задачи с использованием кубиковможно рассматривать как средство реализации гуманитарной направленности в обучении математике.Они способствуют: развитию пространственного воображения; формированию умений мысленно представлять различные положения предмета и изменения его положения в зависимости от разных точек отсчета и умения зафиксировать это представление на изображении; обучению логическим обоснованиям геометрических фактов; развитию конструкторских способностей, моделированию; развитию исследовательских навыков.

Рассмотрим ряд задач, где на гранях кубика или его вершинах нанесены буквы русского или латинского алфавита.

Задача № 1. Дано изображение кубика, на гранях которого проставлены буквы Б, В, Н (рис. 1 а). Расставьте на развертках этого кубика (рис. 56 б-г) буквы в соответствии с уже намеченными. Перерисуйте данные изображения, вырежьте их, расставьте на них буквы и проверьте свой ответ.

Задача № 2. Куб (рис. 3 а) перевернули без проскальзывания так, что он встал на окрашенную грань. Укажите новое положение точки А?

Задача № 3. Кубик с выделенными вершинами А и В (рис. 4а) насадили на ось, проходящую через середины противоположных граней, и повернули вокруг этой оси. Новое положение точки А отмечено на рисунке 4 б) с изображением того же кубика. Отметьте на втором рисунке новое положение точки В.

Задача № 4. На рис. 6а,б изображены куб и его развертка. Обозначьте на развертке точки, соответствующие вершинам куба А, В, С.

Задача № 5. На гранях непрозрачного кубика написаны буквы так, как показано на рис. 7а. Кубик подбросили, и он упал так, что одна из букв стала располагаться, как показано на рис. 7б. Нанесите на остальные грани кубика соответствующие буквы (они могут оказаться повернутыми). Проверьте свой ответ с помощью модели куба.

Задача № 6. Подбросили кубик (рис. 8а) так, что он упал, как показано на рис. 8б заполните пустые видимые грани куба.

Задача № 7. Все кубики на рис. 9а одинаковы. Перечертите развертку одного из кубиков (рис. 9б) и нанесите не нее недостающие буквы.

Задача № 8. Правильно изобразив сдвинутые между собой три прямоугольные проекции кубиков с буквами, прочтите русскую народную мудрость (рис. 10а).
Ответ.Леность – мать пороков (рис. 10б).

Задача № 9. Какие фигуры являются разверткой куба (рис. 11), а какие нет? Объясните. По каким ребрам нужно разрезать куб (рис. 11д), чтобы получить развертки?

Ответ. Фигура а) (рис. 11) не является разверткой куба, поскольку если одну из граней считать за нижнюю грань (рис. 12 а), то, отметив боковые грани (б), убедимся, что их пять, а не четыре.

Фигура г) (рис. 11) разверткой куба не является, так как у куба в каждой вершине должно сходиться три ребра, в то время как у фигуры б) (рис. 12) в точке А это требование нарушается.
Для случая б) (рис. 12) предложенная фигура является разверткой куба. Выберем нижнюю грань (закрашенная) как на рис. 13 а), остальные будут боковыми (б), одна – верхняя (в). Такой куб можно разрезать по выделенным ребрам ВА, МА, МК, KD, MN, NP и РС так, как показано на рис. 13 б). Это одно из возможных решений.

Если в фигуре б) (рис. 11) принять за нижнюю другую грань куба, как показано на рис. 14 а), то разрез по ребрам будет другим: АМ, MN, NP, NB, KP, BC, CD (рис. 14 б).

На рис. 11 разверткой куба является фигура в). Получение такой развертки изображено на рис 15 а).
Тогда данный куб можно разрезать по ребрам, составляющим ломанную CDAMKPNB (рис. 15 б).

Задача № 10. Из картона склеен кубик, на гранях которого нанесены буквы. На рис. 16а дан один вариант развертки этого кубика с изображением букв на его гранях.

Нанесите буквы на пустые грани другого варианта развертки этого кубика (рис. 16б-г).

Задача № 11. Если вы догадаетесь, как расположить буквы на кубиках (на передних гранях), то буквы на верхних гранях составят новое слово (рис. 18).
Ответ.KITTEN – MONKEY.

Задача № 12. По каким ребрам можно разрезать куб (рис. 19 а), чтобы получить изображенную на рис. 19 б развертку?

Источник