Бросаем две игральные кости какова вероятность что в сумме выпадет 10
В случайном эксперименте бросают две
В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 10 очков. Результат округлите до сотых.
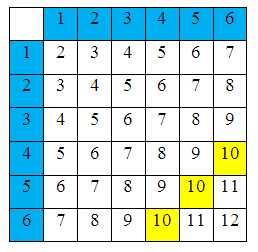
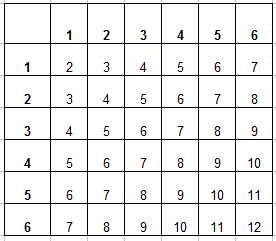
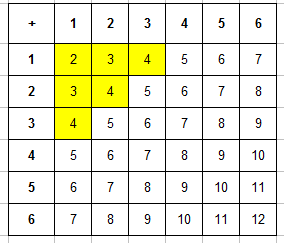
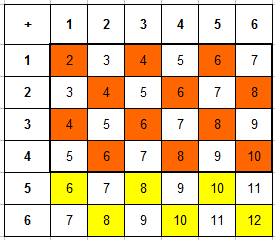
В подобных задачах для удобства решения лучше составить таблицу сумм для вариантов выпадения двух костей (это все комбинации выпадения очков — синим отмечены очки):
Всего элементарных исходов 36 (6 на 6). Благоприятных исходов 3 (легко определить в таблице). Вероятность того, что в сумме выпадет 10 очков, равна 3 к 36 или 0,08333333…. Округляем до сотых, получаем 0,08.
*Если в подобных задачах (на две игральные кости) будет идти речь о сумме выпавших очков, или их произведении, то обязательно составьте таблицу соответственно сумм или произведений. По ней вы легко определите количество чисел.
В фирме такси в данный момент свободно 25 машин: 10 черных, 2 желтых и 13 зеленых. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчице. Найдите вероятность того, что к ней приедет не зеленое такси.
Возможное число исходов 25 (число всех машин). Сказано, что приедет не зелёное такси. Это означает, что приедет либо черное, либо жёлтое такси. Таким образом, число благоприятных исходов 10+2=12. Искомая вероятность равна 12 к 25 или 0,48
Фабрика выпускает сумки. В среднем на 150 качественных сумок приходится 12 сумок со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется некачественной. Результат округлите до сотых.
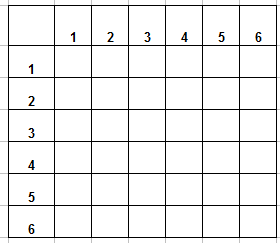
Сказано, что «на 150 качественных» сумок приходится 12 с дефектами. Значит число всех возможных исходов 150+12=162. Число благоприятных исходов 12 (некачественные сумки). Вероятность того, что купленная сумка окажется качественной равна 12 к 162:
Округляем до сотых, получаем 0,07.
Посмотрите ещё задачи на классическую вероятность:
Бросаем две игральные кости какова вероятность что в сумме выпадет 10
Игральную кость бросили два раза. Известно, что шесть очков не выпали ни разу. Найдите при этом условии вероятность события «сумма выпавших очков окажется равна 2».
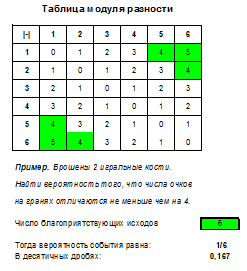
Условию, что при двукратном броске игральной кости шесть очков не выпали ни разу, соответствует 25 исходов (отмечены оранжевым цветом). Событию «сумма выпавших очков равна 2» соответствует 1 из них (отмечены зелёным цветом). Значит, искомая вероятность равна
Игральную кость бросили два раза. Известно, что два очка не выпали ни разу. Найдите при этом условии вероятность события «сумма выпавших очков окажется равна 12».
Условию, что при двукратном броске игральной кости два очка не выпали ни разу, соответствует 25 исходов (отмечены оранжевым цветом). Событию «сумма выпавших очков равна 12» соответствует 1 из них (отмечены зелёным цветом). Значит, искомая вероятность равна
Игральную кость бросили два раза. Известно, что два очка не выпали ни разу. Найдите при этом условии вероятность события «сумма выпавших очков окажется равна 4».
Условию, что при двукратном броске игральной кости два очка не выпали ни разу, соответствует 25 исходов (отмечены оранжевым цветом). Событию «сумма выпавших очков равна 4» соответствуют 2 из них (отмечены зелёным цветом). Значит, искомая вероятность равна
Игральную кость бросили два раза. Известно, что четыре очка не выпали ни разу. Найдите при этом условии вероятность события «сумма выпавших очков окажется равна 11».
Условию, что при двукратном броске игральной кости четыре очка не выпали ни разу, соответствует 25 исходов (отмечены оранжевым цветом). Событию «сумма выпавших очков равна 11» соответствуют 2 из них (отмечены зелёным цветом). Значит, искомая вероятность равна
Бросаем две игральные кости какова вероятность что в сумме выпадет 10
В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 5 очков. Результат округлите до сотых.
Количество исходов, при которых в результате броска игральных костей выпадет 5 очков, равно 4: 2+3, 3+2, 4+1, 1+4. Каждый из кубиков может выпасть шестью вариантами, поэтому общее число исходов равно 6·6 = 36. Следовательно, вероятность того, что в сумме выпадет 5 очков, равна
Ответ : 0,11.
Я считая вариантов не 4,а 6,так как 5 и 0 в сумме тоже дадут 5
На игральной кости нет 0.
В случайном эксперименте бросают три игральные кости. Найдите вероятность того, что в сумме выпадет 6 очков. Результат округлите до сотых.
Количество исходов, при которых в результате броска игральных костей выпадет 6 очков, равно 10: 1 + 1 + 4, 1 + 4 + 1, 4 + 1 + 1, 1 + 2 + 3, 1 + 3 + 2, 3 + 1 + 2, 3 + 2 + 1, 2 + 1 + 3, 2 + 3 + 1, 2 + 2 + 2. Каждый из кубиков может выпасть шестью вариантами, поэтому общее число исходов равно 6 · 6 · 6 = 216. Следовательно, вероятность того, что в сумме выпадет 6 очков, равна
В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 10 очков. Результат округлите до сотых.
Количество исходов, при которых в результате броска игральных костей выпадет 10 очков, равно 3: 4+6, 5+5, 6+4. Каждый из кубиков может выпасть шестью вариантами, поэтому общее число исходов равно 6·6 = 36. Следовательно, вероятность того, что в сумме выпадет 10 очков, равна
Ответ : 0,08.
Ваше решение: Количество исходов, при которых в результате броска игральных костей выпадет 10 очков, равно 3: 4+6, 5+5, 6+4. Я думаю, что будет 4 исхода, так как вероятность что выпадет две пятёрки увеличина вдвое т.к. если бы на однок кости была бы пометочка, то можно было бы видеть, что иногда выпадает 5:5. (с точкой) или 5.:5. Поэтому думаю, что будет 4 варианта 4+6, 5+5, 5+5, 6+4
Максим Ваше рассуждение ошибочно.
Если на одной из костей была бы «пометочка», то вариант 5.:5. невозможен.
Вариант «две пятерки» возможен только в одном случае, если на первом кубике выпадает пятерка и при этом на втором кубике тоже выпадает пятерка.
В случайном эксперименте бросают три игральные кости. Найдите вероятность того, что в сумме выпадет 16 очков. Результат округлите до сотых.
Это задание ещё не решено, приводим решение прототипа.
В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 8 очков. Результат округлите до сотых.
Количество исходов, при которых в результате броска игральных костей выпадет 8 очков, равно 5: 2+6, 3+5, 4+4, 5+3, 6+2. Каждый из кубиков может выпасть шестью вариантами, поэтому общее число исходов равно 6·6 = 36. Следовательно, вероятность того, что в сумме выпадет 8 очков, равна
Ответ : 0,14.
В случайном эксперименте бросают три игральные кости. Найдите вероятность того, что в сумме выпадет 7 очков. Результат округлите до сотых.
Это задание ещё не решено, приводим решение прототипа.
В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 8 очков. Результат округлите до сотых.
Количество исходов, при которых в результате броска игральных костей выпадет 8 очков, равно 5: 2+6, 3+5, 4+4, 5+3, 6+2. Каждый из кубиков может выпасть шестью вариантами, поэтому общее число исходов равно 6·6 = 36. Следовательно, вероятность того, что в сумме выпадет 8 очков, равна
Ответ : 0,14.
В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 2 очка. Результат округлите до сотых.
Это задание ещё не решено, приводим решение прототипа.
В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 8 очков. Результат округлите до сотых.
Количество исходов, при которых в результате броска игральных костей выпадет 8 очков, равно 5: 2+6, 3+5, 4+4, 5+3, 6+2. Каждый из кубиков может выпасть шестью вариантами, поэтому общее число исходов равно 6·6 = 36. Следовательно, вероятность того, что в сумме выпадет 8 очков, равна
Ответ : 0,14.
В случайном эксперименте бросают три игральные кости. Найдите вероятность того, что в сумме выпадет 15 очков. Результат округлите до сотых.
Это задание ещё не решено, приводим решение прототипа.
В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 8 очков. Результат округлите до сотых.
Количество исходов, при которых в результате броска игральных костей выпадет 8 очков, равно 5: 2+6, 3+5, 4+4, 5+3, 6+2. Каждый из кубиков может выпасть шестью вариантами, поэтому общее число исходов равно 6·6 = 36. Следовательно, вероятность того, что в сумме выпадет 8 очков, равна
Ответ : 0,14.
В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 6 очков. Результат округлите до сотых.
Это задание ещё не решено, приводим решение прототипа.
В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 8 очков. Результат округлите до сотых.
Количество исходов, при которых в результате броска игральных костей выпадет 8 очков, равно 5: 2+6, 3+5, 4+4, 5+3, 6+2. Каждый из кубиков может выпасть шестью вариантами, поэтому общее число исходов равно 6·6 = 36. Следовательно, вероятность того, что в сумме выпадет 8 очков, равна
Ответ : 0,14.
В случайном эксперименте бросают три игральные кости. Найдите вероятность того, что в сумме выпадет 13 очков. Результат округлите до десятых.
Это задание ещё не решено, приводим решение прототипа.
В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 8 очков. Результат округлите до сотых.
Количество исходов, при которых в результате броска игральных костей выпадет 8 очков, равно 5: 2+6, 3+5, 4+4, 5+3, 6+2. Каждый из кубиков может выпасть шестью вариантами, поэтому общее число исходов равно 6·6 = 36. Следовательно, вероятность того, что в сумме выпадет 8 очков, равна
Ответ : 0,14.
Решение задач о бросании игральных костей
Обычно задача звучит так: бросается одна или несколько игральных костей (обычно 2, реже 3). Необходимо найти вероятность того, что число очков равно 4, или сумма очков равна 10, или произведение числа очков делится на 2, или числа очков отличаются на 3 и так далее.
Ознакомившись с методами решения, вы сможете скачать супер-полезный Excel-файл для расчета вероятности при бросании 2 игральных костей (с таблицами и примерами).
Одна игральная кость
Пример 1. Игральная кость брошена один раз. Какова вероятность, что выпало четное число очков?
Пример 2. Брошен игральный кубик. Найти вероятность выпадения не менее 5 очков.
Даже не вижу смысла приводить еще примеры, переходим к двум игральным костям, где все интереснее и сложнее.
Две игральные кости
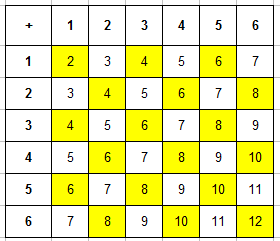
Пример 3. Одновременно бросают 2 игральные кости. Найти вероятность того, что в сумме выпадет менее 5 очков.
Вот и пришло время заполнять таблицу. В каждую ячейку занесем сумму числа очков выпавших на первой и второй кости и получим уже вот такую картину:
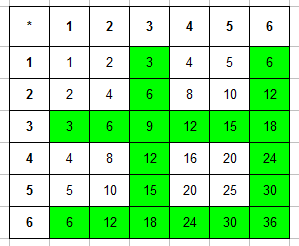
Пример 4. Брошены две игральные кости. Найти вероятность того, что произведение числа очков делится на 3.
Составляем таблицу произведений очков, выпавших на первой и второй кости. Сразу выделяем в ней те числа, которые кратны 3:
Как видно, и этот тип задач при должной подготовке (разобрать еще пару тройку задач) решается быстро и просто. Сделаем для разнообразия еще одну задачу с другой таблицей (все таблицы можно будет скачать внизу страницы).
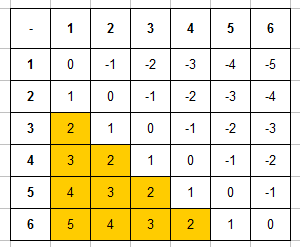
Пример 5. Игральную кость бросают дважды. Найти вероятность того, что разность числа очков на первой и второй кости будет от 2 до 5.
Запишем таблицу разностей очков, выделим в ней ячейки, в которых значение разности будет между 2 и 5:
Итак, в случае, когда речь идет о бросании 2 костей и простом событии, нужно построить таблицу, выделить в ней нужные ячейки и поделить их число на 36, это и будет вероятностью. Помимо задач на сумму, произведение и разность числа очков, также встречаются задачи на модуль разности, наименьшее и наибольшее выпавшее число очков (подходящие таблицы вы найдете в файле Excel).
Другие задачи про кости и кубики
Конечно, разобранными выше двумя классами задач про бросание костей дело не ограничивается (просто это наиболее часто встречаемые в задачниках и методичках), существуют и другие. Для разнообразия и понимания примерного способа решения разберем еще три типовых примера: на бросание 3 игральных костей, на условную вероятность и на формулу Бернулли.
Пример 6. Бросают 3 игральные кости. Найдите вероятность того, что в сумме выпало 15 очков.
В случае с 3 игральными костями таблицы составляют уже реже, так как их нужно будет аж 6 штук (а не одна, как выше), обходятся простым перебором нужных комбинаций.
Теперь подберем такие исходы, которые дают в сумме 15 очков.
Пример 7. Бросают 2 игральные кости. Найти вероятность того, что на первой кости выпало не более 4 очков, при условии, что сумма очков четная.
Пример 8. Игральный кубик брошен 4 раза. Найти вероятность того, что четное число очков выпадет ровно 3 раза.
В случае, когда игральный кубик бросается несколько раз, а речь в событии идет не о сумме, произведении и т.п. интегральных характеристиках, а лишь о количестве выпадений определенного типа, можно для вычисления вероятности использовать формулу Бернулли.
Приведем еще пример, решаемый аналогичным образом.
Пример 9. Игральную кость бросают 8 раз. Найти вероятность того, что шестёрка появится хотя бы один раз.
Полезные ссылки
Для наглядного и удобного расчета вероятностей в случае бросания двух игральных костей я сделала
Файл с таблицами для расчета вероятности.
В нем приведены таблицы суммы, произведения, разности, минимума, максимума, модуля разности числа очков.
Вводя число благоприятствующих исходов в специальную ячейку вы получите рассчитанную вероятность (в обычных и десятичных дробях). Файл открывается программой Excel.
Еще по теории вероятностей:
В решебнике вы найдете более 400 задач о бросании игральных костей и кубиков с полными решениями (вводите часть текста для поиска своей задачи):